相位激电和时域激电对激电效应响应关系研究

郭 鹏 ， 肖 都 ，石福升 ， 林品荣

(中国地质科学院 地球物理地球化学勘查研究所, 廊坊 065000)

0 引言

近年来，相位激电法以其快速、轻便、对弱异常发现能力强等特点广受关注，并在矿产普查与详查中得到广泛应用[1-4]。相位激电法测量交流电场作用下的岩(矿)石的电化学极化效应,即测量电极间总场电位差相对供电电流所产生的相位差,即复电阻率的相位角[5]，它反映的是极化效应的“纯异常”。在低频工作条件下,相位移的大小可以反映地下介质激电效应的强弱。对于一定的频率,激电效应越强,负相位移的绝对值越大；反之,激电效应越弱,负相位移的绝对值越小。激电相位与时间域激电测量的极化率同样是反映岩(矿)石激电效应强弱的参数，二者之间是否存在某种联系，学者们在这方面做了一些工作，分别得到了不同的结果[6-7]。作者结合柯尔-柯尔模型与实测数据对激电相位和极化率之间的联系做了分析。

1 数值模拟激电相位与极化率的变化规律

在激电的频谱特性研究中，国内外学者通常引用柯尔-柯尔模型，其表达式如式(1)。

(1)

其中：ρ0为零频时的电阻率；m为极化率；c为频率相关系数；τ为时间常数。

柯尔-柯尔模型描述了激电效应引起的复电阻率随频率的变化。根据式(1)即可计算出用柯尔-柯尔模型表达式表示的复电阻率的虚、实分量和振幅、相位频谱。

从柯尔-柯尔模型得到相位表达式

φ(ω)=

(2)

式(2)中同时包含了相位和极化率参数，但其关系不是简单的对应关系，相位是一个包含极化率、时间常数、频率和频率相关系数的综合参数，很难根据式(2)简单定义相位和极化率的相互关系。为此考虑使用数值模拟的方法，通过绘制极化率与相位关系图，来分析极化率和相位的关系。数值模拟中分别考虑了不同频率相关系数、时间常数和不同频率下的相位随极化率的变化情况，并在不同坐标系下进行绘图如图1所示。

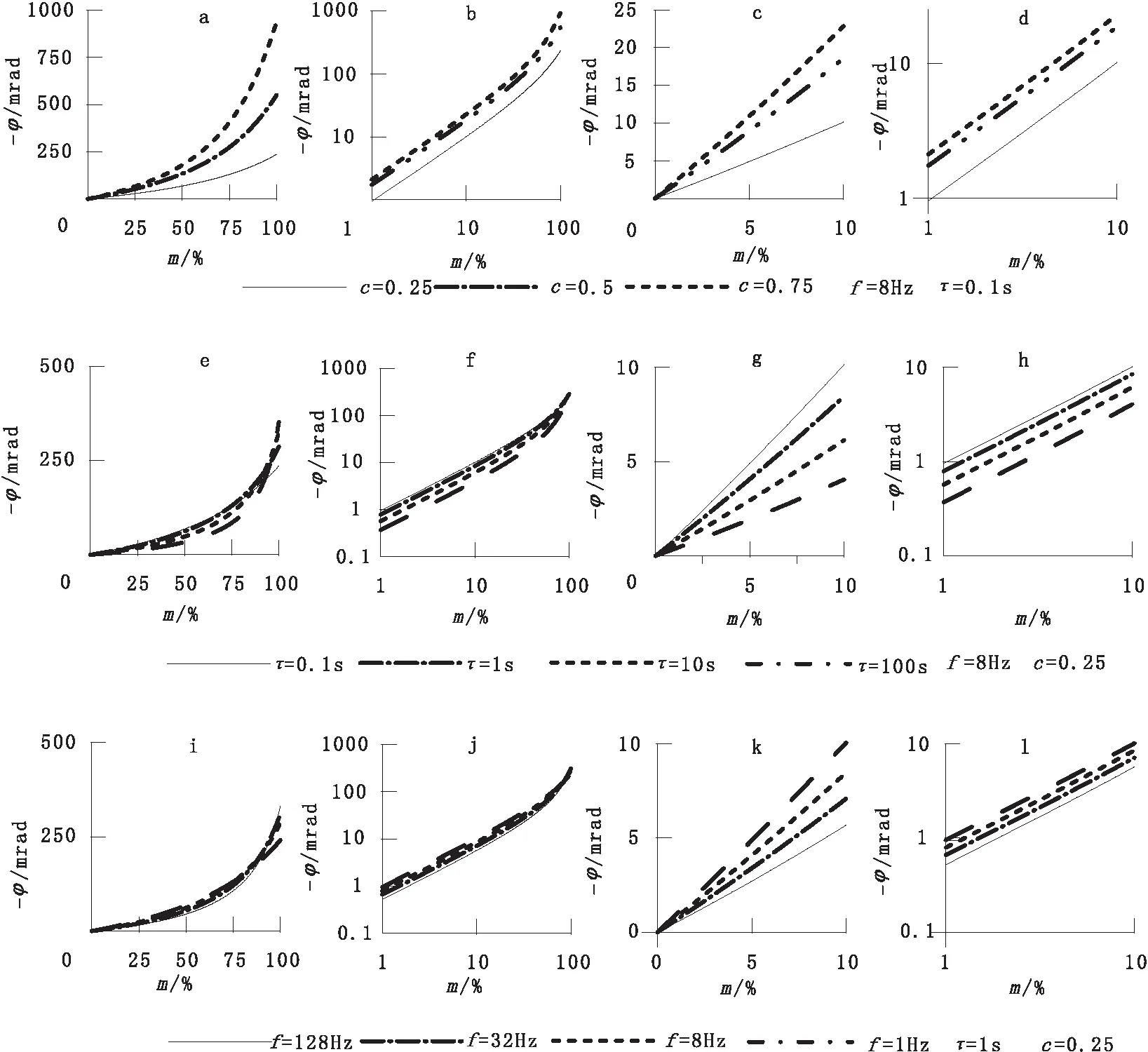
图1 相位随极化率变化图Fig．1 Phase change with polarization

从图1中可以看到，在算术坐标下，极化率从0 %～100 %范围内(图1中(a)、(e)、(i))，在不同的c值、τ值和f值时，相位都随极化率的增大而增大，呈现非线性变化；而在极化率较小时(≤10%)，相位和极化率在算术坐标下呈现出近似线性变化的关系(图1中(c)、(g)、(k))，只是由于c值、τ值和f值的差异，该曲线的斜率存在不同。由此我们给出在极化率较小时，相位与极化率近似满足关系式

φ≈k·m+b

(3)

其中：k为曲线的斜率，其大小与频率、时间常数和频率相关系数有关；b为线段在y轴上的截距。

在双对数坐标下，相位随极化率的增大而单调增加，极化率从0 %～100 %范围内呈现非线性变化(图1中(b)、(f)、(j))；在极化率较小时(≤10%)相位与极化率呈现出近似线性变化的规律(图1中(d)、(h)、(l))。曲线斜率在不同频率、时间常数和频率相关系数下基本保持不变。

从上述相位随极化率的变化规律给出在双对数坐标下，极化率较小时(≤10 %)相位随极化率变化的近似关系式

logφ≈k1·logm+b1

(4)

其中：k1为线段的斜率，为一常数；b1为线段在y轴上的截距，其大小与频率、时间常数和频率相关系数有关。

由图1结合上面关系式(3)与关系式(4)分析可得，在极化率≤10%的情况下(这种情况包括了绝大多数时间域激电实测视极化率数值)，在算术坐标和双对数坐标下，相位与极化率都呈现出近似线性关系。不同点是，在算术坐标下，频率、时间常数和频率相关系数的变化，影响曲线斜率k的变化；在双对数坐标下频率、时间常数和频率相关系数的变化，则是影响到线段在y轴上的截距b1的变化。

2 实测激电相位随视极化率变化规律

在得到算术坐标和双对数坐标系下相位与极化率的关系式(3)与关系式(4)后，究竟哪一个关系式更贴近实际情况，为此在内蒙某矿区进行了野外同装置、同测点的相位激电和时间域激电数据采集工作，将野外采集数据进行了算术坐标系和双对数坐标系下的对比。

工作中分别采集了中梯装置和偶极-偶极装置下的时间域视极化率和频率域激电相位数据。时间域激电选用的供电周期为16 S，供电电流为7 A，数据采集断电延时的时间为100 ms，数据的采样宽度为160 ms。相位激电观测频率为4 S,供电的电流为5 A。中梯装置的供电极距为1 500 m，接收极距为40 m；偶极-偶极装置AB=MN=80 m，点距为40 m，隔离系数n= 3～8。

图2是中梯装置下，将采集的65个测点的相位激电和时间域激电数据绘制成图。从图2中可见,算术坐标系下数据点的分布较双对数坐标系下的离散度要小。算术坐标系下的数据更接近于线性关系。

图3是偶极-偶极装置下采集的513个测点的实测相位和视极化率数据绘制成图。从图3中可见,算术坐标系下，极化率数据点分布，较双对数坐标系下的离散度要小的多。从数据点总体分布来看，算术坐标系下的数据点分布更接近于线性关系。

从野外实测数据分析发现，激电相位和视极化率在算术坐标系下更接近于线性关系，因此式(3)更接近于实测相位和极化率的分布规律。

根据关系式(3)，使用直线来拟合这些数据点，确定k值和b值如图4所示。计算得中梯装置下k值为6.86，b值为 -3.18,激电相位与视极化率相互转换关系式为：

φ=6.86·η-3.18；η=(φ+3.18)/6.86

(5)

偶极-偶极装置下k值为6.84，b值为-0.75，激电相位与视极化率相互转换关系式为：

φ=6.84·η-0.75;η=(φ+0.75)/6.84

(6)

3 验证关系式

在各个参数确定后，进行了视极化率和激电相位的相互转换对比，验证转换公式的适用性。图5和图6是该矿区，中梯装置观测的激电相位和视极化率相互转换对比图。从图中可见，由视极化率转换的激电相位与实测激电相位数值大小非常相近，曲线形态完全一致；由激电相位转换的视极化率，与实测视极化率的数值和曲线形态，同样具有良好的一致性。

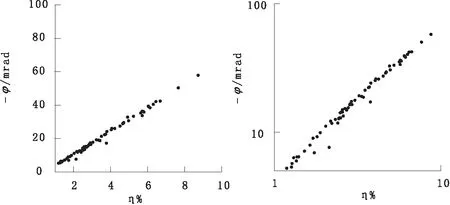
图2 中梯装置不同坐标系下视相位与视极化率关系图

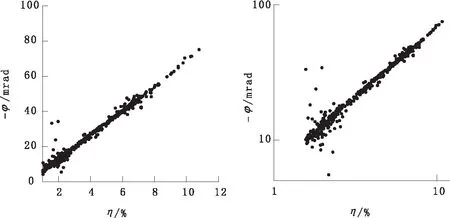
图3 偶极-偶极装置不同坐标系下相位与视极化率关系图Fig．3 Relation of apparent phase and apparent polarization under dipole-dipole device in different coordinate system

图7和图8是该矿区122线偶极-偶极装置下，绘制的视极化率和激电相位相互转换断面对比图。如图中所示，视极化率和激电相位相互转换绘制的断面图，与实测视极化率和激电相位断面图异常形态、异常位置相同，实测数值与转换数值大小接近，具有很好的一致性。

4结论

通过数值模拟和实测数据分析表明，激电相位和时间域激电极化率对激电效应的反映是相同的，在一定条件下，激电相位和视极化率可进行相互转换。

图4 直线拟合数据点图Fig．4 Fitting a straight line

图5 内蒙某矿区122线激电相位与视极化率相互转换对比图

图6 内蒙某矿区126线激电相位与视极化率相互转换对比图

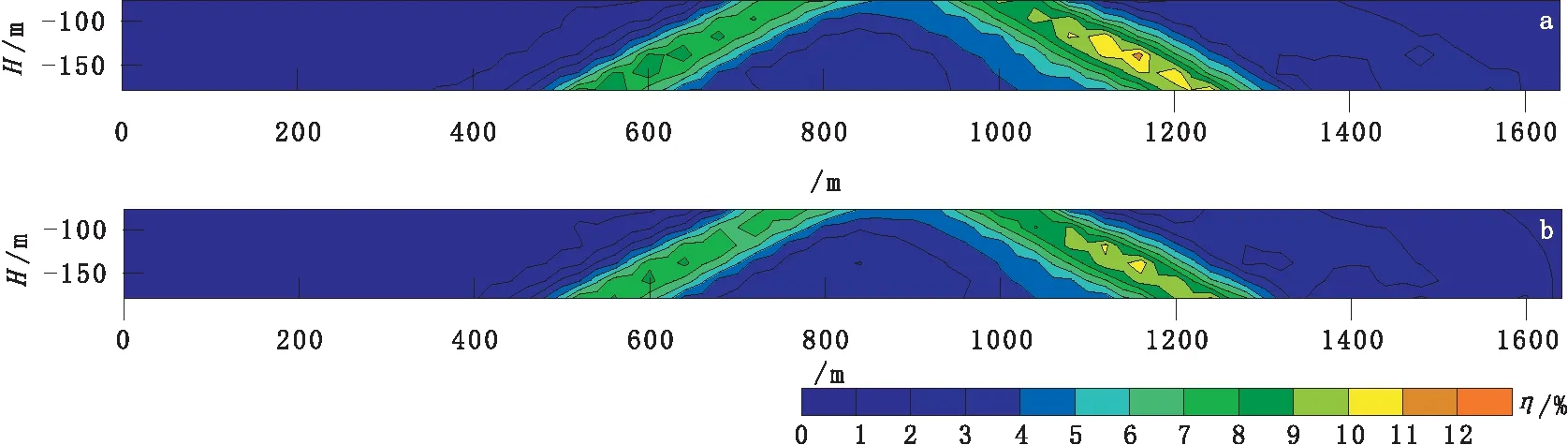
图7 内蒙古某矿区122线激电相位转换视极化率测深断面对比图

图8 内蒙古某矿区122线视极化率转换激电相位测深断面对比图

参考文献：

[1] 林品荣．电磁法综合探测系统研究[J]．地质学报，2006，80(10)：1539-1548.

[2] 郭鹏，肖都，石福升．阵列相位激电法在弱极化异常区的试验效果[J] 物探与化探，2012，36(5)：772-774.

[3] 刘瑞德，陆桂福，张强，等．相位激发极化在宁波油气勘探中的应用[J]．地质与勘探，2004，40(增刊)：14-16.

[4] 李建华，林品荣，徐宝利，等．阵列相位激电法与时域激电法的对比分析[J]．物探化探计算技术，2007，29(增刊)：98-100.

[5] 刘崧．谱激电法[M]．北京：中国地质大学出版社，1998．

[6] 王书民，雷达．相位激电法(偶极一偶极)单频电磁耦合校正方法[J]物探与化探，2002，26(1)：57-59.

[7] 徐宝利，林品荣．岩矿石标本激电相位和极化率测定及其关系探讨[J]．物探化探计算技术，2006，28(增刊):81-83.