基于双缩尺比的桅杆振动研究
,,, ,
(1. 华中科技大学 船舶与海洋工程学院,武汉 430074;2. 中国舰船研究设计中心,武汉 430064)
根据要求,需要设计桅杆缩尺模型并进行振动、强度试验。桅杆为筒状薄壁结构,与传统的桁架结构差别很大[1]。板材厚度(包括加强筋)的范围为3~8 mm,根据合同要求确定几何缩尺比为1∶6。如果为单一缩尺比,那么缩尺模型的板厚范围为0.5~1.3 mm,这样薄的钢板在市场难以购买;而且,在与其上的加强筋焊接过程中薄板容易熔穿,且很难控制薄板的变形,这会降低试验结果的可靠性,甚至会中断模型制作使试验无法进行。基于上述因素,拟采用双缩尺比,即桅杆的主尺度(长、宽、高)采用a=1∶6,板厚采用b=1∶2(加强筋与其相似)。缩尺模型的板材厚度范围为1.5~4.0 mm,这样的板材市场上容易购买且在焊接中易于控制变形。
1 桅杆的相似理论
用大写字母表示原型的各量,小写字母表示缩尺模型的各量[2]。
1.1 剖面惯性矩
将桅杆横截面上各构件分割成一些小段,则原型与模型的剖面惯性矩为

(1)
式中:Bi,Ti,Zi——桅杆原型中小段板的宽度、厚度和形心到中性轴距离;
bi,ti,zi——桅杆模型中小段板的宽度、厚度和形心到中性轴距离。
桅杆模型中的各个字母分别与原型相对应。
1.2 总体弯曲振动
桅杆原型与模型的模态频率分别为

(2)
式中:K——由边界条件、截面惯性矩及质量沿桅杆高度分布规律决定的系数,原型与模型的K相同;
L——桅杆高度;
E——弹性模量;
M——桅杆单位长度的质量,M正比于BT。
其中:B——桅杆宽度。

1.3 总体扭转振动
截面扭转刚度为GJp(G为剪切模量;Jp为扭转惯性矩),与弯曲惯性矩的量纲相同。桅杆模型与原型的惯性矩之比为
(3)
截面转动惯量为
Ip=irJp
(4)
加强筋对Jp没有贡献,但对Ip有贡献,用i计及此种差异,原型和模型有相同的i。桅杆原型与模型的模态频率分别为
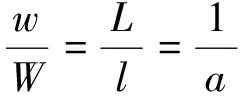
(5)
在双缩尺比下,弯曲振动和扭转振动有着相同的相似规律。
1.4 加筋板振动
板架振动对于桅杆系统是一个局部振动,它对桅杆的整体振动会产生影响(即当两者的频率接近时会产生耦合)。以下论证中桅杆模型采用双缩尺,加筋板的振动与桅杆整体振动内在关系与桅杆原型保持一致,从而不会因为关系异常而对桅杆缩尺模型的整体振动数据造成误差。
桅杆的板架在两个方向有加强材,记主要加强材方向为x,另一个方向为y;把板架近似为正交异性板,加强材的质量平摊在板上。两个方向的加强材连同板的组合弯曲刚度平摊在板上作为x和y方向的刚度。板架的自由振动方程为
D1[Wxxxx+(1+S)Wxxyy+SWyyyy]+MWtt=0
(6)
式中:D1——组合板x方向单位宽度的弯曲刚度;

下标x,y,t——对坐标x、y以及时间t的微分;
M——组合板单位面积质量。
四边简支的板,方程(1)的解为
(7)
式中:A,B——加筋板x方向,y方向的边长。
将式(7)代入式(6),得

(8)
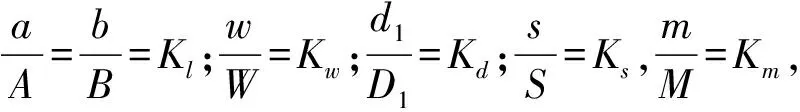
代入式(8),得
模型与原型的方程应有相同形式,必有
(9)
Ks=1
(10)
S是板架x,y方向刚度之比,模型和原型的S相等,因此式(10)成立。
为使板架振动与桅杆整体振动有相同的频率换算关系,前面已经得到

(11)
将式(11)代入式(9)式,得
(12)
Km=b
(13)
式中:b——板厚缩尺比。
将式(13)代入式(12),得
(14)
当按a,b缩尺
可以看出,Kd满足式(14),板架的频率满足式(11)。
2 桅杆有限元模型的建立
2.1 桅杆原型
根据单位提供的图纸,建立实船桅杆有限元模型。由于实船桅杆焊接在01甲板,因此初始模型考虑01甲板在内的以上结构,其它的作为边界条件。为了使缩尺模型的制作尽可能简化以减少制作工时,在保持桅杆振动和强度性能一致的前提下,将实船桅杆一步步简化,包括简化了实船桅杆模型部分甲板、大桅主体舱室门;考虑到模型的焊接局限,进一步简化了外围甲板的舱室隔板。最终的桅杆原型结构包括大桅主体、橫桁、小桅以及外围简化的01~05甲板。
桅杆原型的边界条件[3]为01甲板四周取为简支,在Fr121肋位设有一道横舱壁,此处也取为简支。桅杆原型和缩尺模型的有限元模型都基于patran软件[4]建立(见图1),应用的单元类型为板单元、梁单元和质量单元。其中板单元模拟模型的甲板板、舷侧板、舱室隔板、桅杆围板、桅杆平台、小桅板、横桁板,以及起加强作用的肘板等结构;梁单元模拟甲板纵骨、甲板纵桁、甲板横骨、甲板强横梁、舷侧肋骨、强肋骨、大桅围板和舱室隔板的加强筋等结构;质量单元用于模拟安装在小桅、横桁、大桅外部甲板和内部甲板以及桅杆围板上的设备。

图1 桅杆原型有限元模型
2.2 桅杆缩尺原型
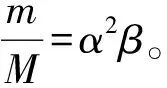
以下以桅杆原型中间距为500 mm的2根T型材作说明。
如图2所示,上部分为桅杆原型结构经过双缩尺比后某局部板的T型材,而下部分为其等效简化后对应缩尺模型的角钢,而角钢的3个要素即面板高、腹板高和厚度可以通过上下图加强材与带板的截面积、组合惯性矩以及截面质量中心高度分别相等列方程解出。

图2 缩尺模型中等效简化前后型材对比
桅杆缩尺模型的有限元模型见图3。

图3 桅杆缩尺模型有限元模型
3 桅杆原型与缩尺模型的振动
考虑到桅杆结构的整体振动和局部振动[5-6],分别提取了桅杆原型和缩尺模型的整体一阶横向振动、整体一阶纵向振动、整体一阶扭转振动、小桅横向振动、小桅纵向振动、平台振动、横桁横向振动、横桁纵向振动的频率来进行对比,桅杆原型和缩尺模型的整体一阶横向振动模态见图4,5。(其它状态振动模态图省略)。

f=12.622 Hz图4 桅杆原型一阶横向振动

f=78.35 Hz
桅杆原型和缩尺模型的各个振动频率以及相对误差见表1(相对误差是指桅杆缩尺模型频率按相似理论换算后与桅杆原型比较的误差,其中换算值为1/6)。

表1 桅杆原型和缩尺模型的各个振动频率和相对误差
4 结论
从表1数据分析来看,除小桅纵向振动这个局部振动误差相对较大外其它振动误差都较小,基本符合桅杆相似理论的推论,证明了基于双缩尺比桅杆模型设计的科学性与可行性;而对于小桅纵向振动来说,误差相对较大是因为频率基数较小,并且局部振动相对于整体振动来说是次要的。
实际上,为了以后缩尺模型制作方便、缩短工时且控制焊接变形才将加强筋等效简化,而在桅杆原型中少数部位或者骨材为奇数,或者骨材布置不均衡,而对于此种情况缩尺模型中只能作近似等效,因此造成了部分误差。总体来说,基于双缩尺比的桅杆模型振动为以后研究原型与模型相互间的振动规律提供了较高的参考价值。
[1] Murty K S M,Yohanna M F W,Gerard R M.Dynamic response of guyed masts [J].Engineering Structure,1998, 20(12):1097-1101.
[2] 金咸定,赵德有.船体振动学[M].上海:上海交通大学出版社,2000.
[3] 杨振财, 赵德有.船舶筒形桅杆振动分析中边界条件的研究[J].中国海洋平台,2006,21(2):17-23.
[4] 龙 凯,贾长治,李宝峰.Patran 2010与Nastran 2010有限元分析从入门到精通[M].北京:机械工业出版社,2011.
[5] 姚熊亮,曾令玉,杨文山,等.综合集成桅杆振动特性研究[J].船舶工程,2009,31(增刊):12-16.
[6] 郎济才, 姚熊亮,邵长青.船舶筒状桅杆的模态分析[J].舰船科学技术,2006,28(4):26-28.

