运动副间隙对多杆锁机构动力学特性的影响

智常建，王三民，孙远涛

运动副间隙对多杆锁机构动力学特性的影响

智常建，王三民，孙远涛

（西北工业大学机电学院，710072西安）

为降低因受力异常而出现飞机货舱门意外打开的概率，详细研究运动副间隙对多杆锁机构动力学特性的影响.采用无质量的等效间隙杆描述运动副的间隙，以拉格朗日动力学方程和螺旋理论为基础建立了多杆锁机构的动力学分析模型，并用MATLAB软件编程对模型进行了求解分析.结果表明：杆的角速度、角加速度、驱动力矩和铰链约束力对运动副间隙的大小比较敏感，在奇异位型附近受到的影响最大.间隙为10μm时，其对多杆锁机构的动力学影响较小；间隙为100μm时，其对多杆锁机构的动力学影响明显增强.

运动副间隙；多杆锁机构；螺旋理论；等效间隙杆；动力学特性

多杆锁机构广泛应用于飞行器的舱门中.多杆锁机构出现锁不紧或打不开的现象，大多是因为其受力出现了异常，而运动副间隙是造成多杆锁机构受力异常的主要原因.运动副间隙对机构动力学性能的影响是机械学研究的热点.考虑运动副间隙的机构动力学模型主要有三类［1］：“接触-分离”的二状态模型；“接触-分离-碰撞”的三状态模型；“连续接触”的连续接触模型（即等效间隙杆）.二状态模型是由Dubowsky等［2-5］提出的，Funabashi等［6］以含间隙的四连杆为对象，对该模型进行了实验验证.周益君等［7］在两状态模型的基础上，建立了三维运动副间隙，综合考虑了杆件弹性对对杆机构的影响.三状态模型最早由Miedema等［8］提出，Soong等［9］对其进行了实验验证，并进一步扩展了该模型.Earles等［10］最早建立了连续接触模型，Furuhashi等［11］对考虑间隙的四连杆机构做了深入研究.白争锋等［12-13］建立了非线性的连续接触碰撞力的混合模型，在嵌入ADAMS软件中分析了运动副间隙对机构动态特性的影响.Tai等［14］采用无质量的等效间隙杆描述间隙，以螺旋理论为基础分析了运动副间隙对多杆机构运动灵敏度与定位误差的影响.

虽然研究运动副间隙对杆机构动力学影响的文献很多，但是直接以多杆锁机构为研究对象的不多，只有刘霞［15］、Tai等［14，16］研究了杆长误差对其运动精度及开锁力影响的影响.本文采用无质量的等效间隙杆描述运动副间隙，基于拉格朗日动力学方程和螺旋理论建立了理想多杆锁机构和考虑间隙的多杆锁机构的动力学特性分析模型，研究了不同间隙值下多杆锁机构的运动规律、驱动力矩和运动副的约束反力，为多杆锁机构的可靠性设计、性能评价和维护等提供参考依据.

1 多杆锁机构及其运动简图

多杆锁机构是典型的瓦特I型机构，运动简图如图1.该机构由两个平面四杆机构组成，工作过程中主动杆6处于浮动状态.杆长的参数如下：l1＝410 mm，l2＝230 mm，l3＝430 mm，l3a＝700 mm，l3b＝315 mm，l4＝210 mm，l4a＝505 mm，l4b＝330 mm，l5＝380 mm，l6＝300 mm.各杆的质量：m2＝1.670 9 kg，m3＝8.669 9 kg，m4＝5.949 0 kg，m5＝1.563 0 kg，m6＝1.327 3 kg.各杆的转动惯量：J2＝677.563 6 kg·mm2，J3＝14 326 kg·mm2，J4＝7 631.552 6 kg·mm2，J5＝292.408 8 kg·mm2，J6＝260.440 kg·mm2.假定主动杆6的运动规律是已知的，即从静止开始，以加速度α＝2 rad·s-2加速上锁.θ6是主动件杆6的角位移，其满足：-50°≤θ6≤125°.为了满足机构的运动条件，主动杆上作用有一驱动力矩Md.为了简化计算模型，暂时先不考虑运动副间的摩擦力，并以铰链12为原点O建立笛卡尔坐标系X O Y.

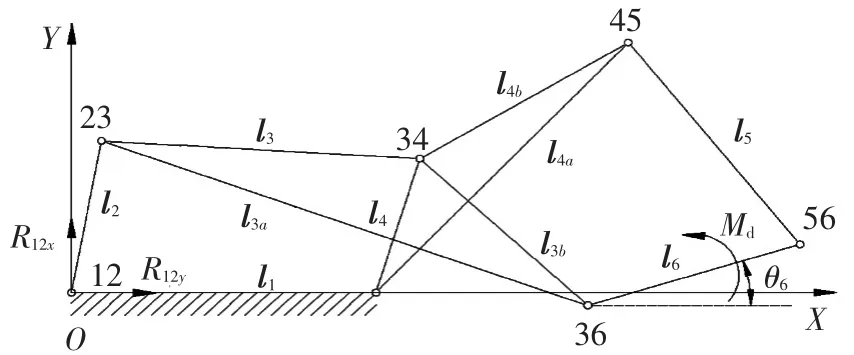
图1 多杆锁机构的运动简图

2 理想多杆锁机构的动力学分析模型

理想的多杆锁机构是单自由度系统，其拉格朗日动力学方程为［17-18］

式中：E为系统的总动能，U为系统的总重力势能，p为广义坐标，M为广义力，.p为广义坐标对时间的导数.

对多杆锁机构，其总动能和重力势能分别为

式中：mi为第i个杆的质量，Ji为第i个杆的转动惯量，xsi为第i个杆质心的横坐标，ysi为第i个杆质心的纵坐标，g为重力加速度，θi为第i个杆的角位移.

将式（2）和（3）代入式（1），可得理想多杆锁机构的拉格朗日动力学方程：

由图1可知，理想多杆锁机构是由两个封闭的四边形组成的，可以得到下列封闭矢量方程：

经过分析，理想多杆锁机构有θ2、θ3、θ4、θ5和θ6总计5个位置变量.选取θ6为广义坐标，则θi（i＝2、3、4、5）4个位变量都是θ6的函数.将式（5）和式（6）展开，可得到与θ6对应的θi（i＝2、3、4、5）的值.分别对式（5）和式（6）的展开式求时间t的一阶导数和二阶导数，可得到与.θ6和¨θ6对应的.θi和¨θi（i＝2、3、4、5）.各杆的质心坐标xsi和ysi、.xsi和.ysi以及¨xsi和¨ysi可以由θi、.θi和¨θi（i＝2、3、4、5、6）表示.由于理想多杆锁机构上只有一个驱动力矩，而且作用在杆6上，所以广义力M即是驱动力矩Md.

为了获得各铰链的动态作用力，需要基于螺旋理论建立多杆锁机构的动态平衡方程［16，19］.作用在理想多杆锁机构第i个杆上的力螺旋为作用在连杆上的外部力螺旋Si（包括惯性力和重力）和铰链约束力螺旋S（i-k）i.理想多杆锁机构中的第i杆的受力如图2，并且当杆i处于动平衡状态时，满足下列关系式［14，16］：

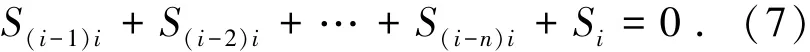
式中：S（i-k）i为杆i-k作用在杆i上的力螺旋，Si为作用在杆i上的外力螺旋.

其中：

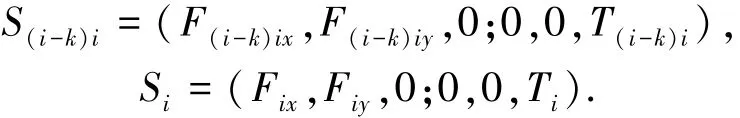
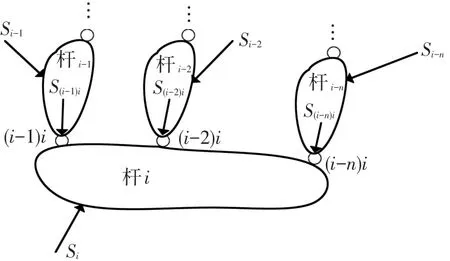
图2 第i杆的受力分析图

多杆锁机构处于动平衡状态时，铰链的约束力螺旋S（i-k）i与运动螺旋＄（i-k）i互易，满足［2-5］

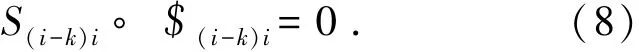
式中：＄（i-k）i＝（0，0，1；y（i-k）i，-x（i-k）i，0）.

式（4）、式（7）和式（8）构成了理想多杆锁机构的动力学分析模型.将式（7）和式（8）展开，可以得到各铰链的约束力F（i-k）i.

3 考虑间隙的多杆锁机构动力学分析模型

在7个铰链处分别引入等效间隙杆，每个间隙杆角位移为独立广义坐标，故考虑间隙的多杆锁机构是8自由度系统，它的拉格朗日动力学方程为［17-18］

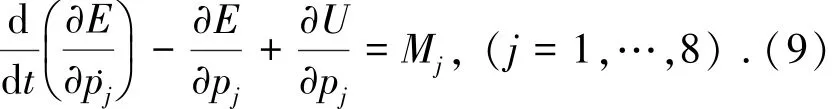
式中各变量的含义与式（1）相同.

将式（2）和式（3）代入式（9），可以得到考虑间隙的多杆锁机构的拉格朗日动力学方程：

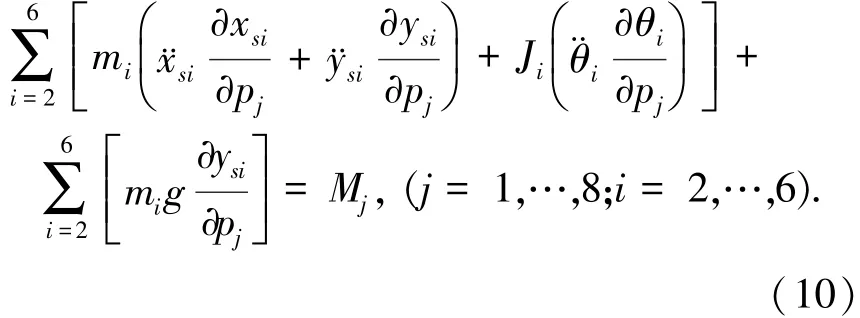
考虑间隙时，要在各运动副的间隙处添加等效间隙杆，其受力见图3.为了便于研究不同间隙对多杆锁机构的影响，本文直接给定各等效间隙杆的杆长，用e表示.

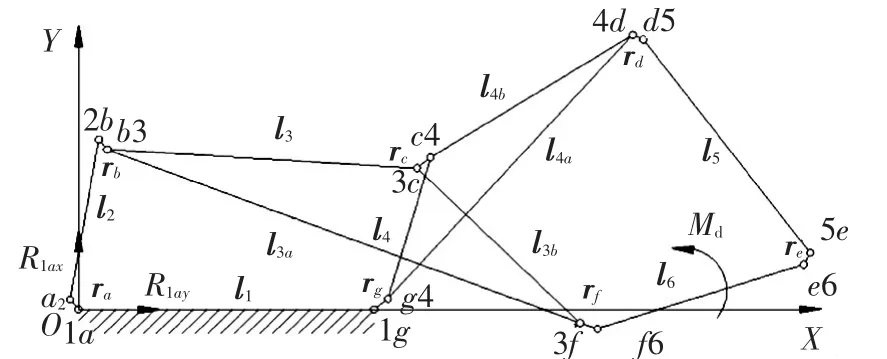
图3 考虑间隙时多杆锁机构的力学分析图

与理想多杆锁机构一样，考虑间隙的多杆锁机构依然是由两个封闭的多杆机构组成的，所以可以得封闭矢量方程：

对考虑间隙的多杆锁机构来说，不但包括θ2、θ3、θ4、θ5和θ6这5个的位置变量，而且还包括各等效间隙杆的位置变量θa、θb、θc、θd、θe、θf和θg.选择θ6、θa、θb、θc、θd、θe、θf和θg作为广义坐标.展开上面的两个矢量方程可以得到4个代数方程.

由于新增的等效间隙杆不受外力的作用，理想多杆锁机构的铰链受力与X轴正方向的夹角可以看做是与该处的等效间隙杆的角位移的初值，即θa、θb、θc、θd、θe、θf和θg是已知的.因此可以由矢量方程求出θ2、θ3、θ4和θ5的值.在很短的时间内（一个步长），假定各间隙杆是匀速运动的，即.θa、.θb、.θc、.θd、.θe、.θf、.θg、¨θa、¨θb、¨θc、¨θd、¨θe、¨θf和¨θg是已知的，且¨θa＝¨θb＝¨θc＝¨θd＝¨θe＝¨θf＝¨θg＝0.

分别对式（11）和式（12）的展开式求时间t的一阶导数和二阶导数，可以得到与.θ6和¨θ6对应的.θi、¨θi（i＝2、3、4、5）.各杆的质心坐标xsi和ysi以及.xsi和.ysi、¨xsi和¨ysi可以由θi、.θi、¨θi（i＝2、3、4、5、6）表示.将它们代入式（10），可得到作用广义力Mj（j＝1，…，8），其中驱动力矩Md＝M1.

式（7）、式（8）和式（10）构成了考虑间隙时多杆锁机构的动力学分析模型.将式（7）和式（8）展开，可得到各铰链的约束力F（i-k）i.

考虑间隙的多杆锁机构动力学模型求解过程如下：1）给定杆位移的求解精度ε.

2）由理想多杆锁机构的铰链约束力求各等效间隙杆的初始角位移.

3）求考虑间隙时各杆的角位移，杆2的角位移为θ2（0）（i的初始值为0）.

任何事情，都有前因后果，都有来龙去脉，在语句中表现为前项和后项。但是第一，如果我们没有找到真正的原因，那么所找的原因就是一个任意因果的原因，而不是必然因果的原因。第二，前项和后项在语句中的完备，不能代替事实中的正确的因果关系。

4）求各铰链约束力和驱动力.

5）由铰链约束力求各等效间隙杆的角位移.

6）求解各杆的角位移，杆2的角位移为θ2（i）.

7）求各铰链约束力和驱动力.

8）判断｜θ2（i）-θ2（0）｜＜ε是否成立，如果不成立，θ2（0）＝θ2（i），i＝i＋1转向6）；如果成立，转向9）.

9）输出各杆的角位移、角速度、角加速度、驱动力矩和铰链约束力.

依据上述求解过程，采用MATLAB语言编写了考虑间隙的多杆锁机构动力学分析程序，对不同间隙下多杆锁机构的动力学特性进行了求解.

4 结果与分析

图4 θ2随驱动杆角位移θ6变化情况

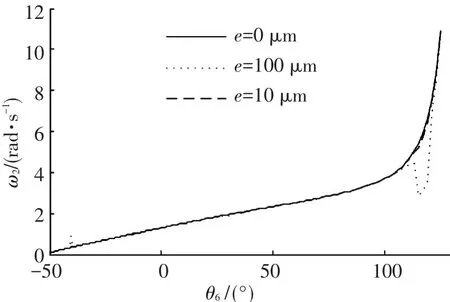
图5 ω2随驱动杆角位移θ6变化情况

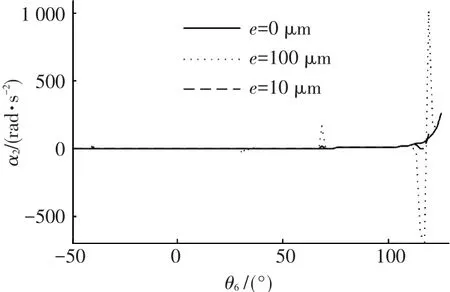
图6 α2随驱动杆角位移θ6变化情况

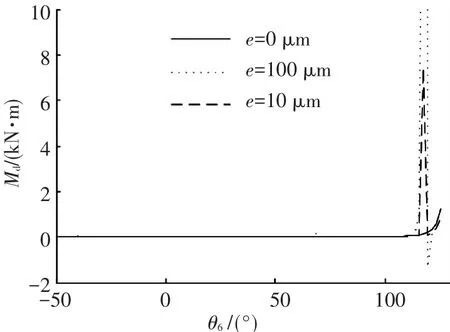
图7 Md随驱动杆角位移θ6变化情况

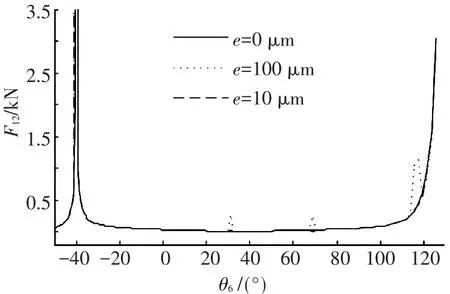
图8 F12随驱动杆角位移θ6变化情况

由图4～8可以看出：

（1）e＝0μm时（不考虑间隙），在工作范围内，θ2、ω2、α2和Md曲线都比较平滑，状态比较稳定.F12在θ6＝-40°处附近出现了突变，原因是多杆锁机构在此时出现了奇异位型.

（2）e≠0μm时（考虑间隙），与理想多杆锁机构相比，θ2的曲线基本重合；ω2、α2、Md和F12的曲线出现了一定的偏差.为了更具体的描述偏差，引入了绝对偏离值的概念，即考虑间隙的值与理想值的差的绝对值.绝对偏离值的最大值反映了偏离的最大幅度，平均值反映了工作范围内的整体偏离情况.具体情况如下：

e＝10μm时，在多杆锁机构的工作范围内，θ2的绝对偏离值的最大值为0.018 4 rad，平均值为0.001 1 rad；ω2的绝对偏离值的最大值为0.212 1 rad·s-1，平均值为0.005 4 rad·s-1；α2的绝对偏离值的最大值为55.051 7 rad·s-2，平均值为1.008 8 rad·s-2；Md的绝对偏离值的最大值为7 275.3 N·m，平均值为47.767 1 N·m；F12的绝对偏离值的最大值为17 044 N，平均值为191.629 3 N.

e＝100μm时，在多杆锁机构的工作范围内，θ2的绝对偏离值的最大值为0.020 3 rad，平均值为0.001 2 rad；ω2的绝对偏离值的最大值为3.098 5 rad·s-1，平均值为0.069 3 rad·s-1；α2的绝对偏离值的最大值为948.615 8 rad·s-2，平均值为15.985 3 rad·s-2；Md的绝对偏离值的最大值为61 080 N·m，平均值为369.001 N·m；F12的绝对偏离值的最大值为166 110 N，平均值为957.481 1 N.

可以看出，运动副间隙对θ2的影响比较小，对ω2、α2、Md和F12的影响明显大于对角位移的影响.间隙越大，θ2、ω2、α2、Md和F12的绝对偏离值的平均值也越大，即影响也越大.对比发现，θ2、ω2、α2和Md的绝对偏离值的最大值都出现在θ6＝117.5°附近，F12的绝对偏离值的最大值出现在-40°附近.原因是多杆锁机构在θ6＝117.5°和θ6＝-40°附近出现了奇异位型.间隙值越大，在奇异位型附近波动的范围和幅度也越大，说明多杆锁机构在奇异位型附近的运动是不稳定的.

5 结 论

1）理想的多杆锁机构在工作范围内的运动是比较稳定的，铰链受力在局部发生突变；

2）多杆锁机构在θ6＝117.5°和θ6＝-40°附近出现了奇异位型.在这两点附近，多杆锁机构对运动副间隙比较敏感，θ2、ω2、α2、Md和F23波动比较大，因此多杆锁机构的上锁和解锁位置设计，尽量避开这两个位置；

3）运动副间隙对多杆锁机构的影响是显而易见的，间隙越大影响也就越大.运动副间隙对多杆锁机构的杆的角位移影响比较小，对杆的角速度、角加速度、驱动力矩和铰链约束力影响比较大；

4）运动副间隙的产生不可避免，只要控制在一定范围内，就可以获得相对稳定的多杆锁机构.运动副间隙足够大时，在奇异位型附近发生振荡的范围比较大，上锁或者解锁过程都会受到较大程度的影响，严重时会影响飞机的安全.在实际的工作中，应根据间隙大小及时地维护或更换货仓门的多杆锁机构.

［1］白争锋.考虑铰间间隙的机构动力学特性研究［D］.哈尔滨：哈尔滨工业大学，2011：5-11.

［2］DUBOWSKY S，FREUDENSTEIN F.Dynamic analysis of mechanical systems with clearance，part 1：formation of dynamic model［J］.Journal of Engineering for Industry，1972，93（1）：305-309.

［3］DUBOWSKY S，FREUDENSTEIN F.Dynamic analysis of mechanical systems with clearances，part 2：dynamic response［J］.Journal of Engineering for Industry，1971，93（1）：305-309.

［4］DUBOWSKY S，GARDNER T N.Dynamic interactions of link elasticity and clearnce connections in planar mechanical systems［J］.Journal of Engineering for Industry，1975，97（2）：652-661.

［5］DUBOWSKY S，DECK J F，COSTELLO H.The dynamic modeling of flexible spatial machine systems with clearance connections［J］.Journal of Mechanisms，Transmissions and Automation in Design，1987，109（1）：87-94.

［6］FUNABASHI H，OGAWA K，HORIE M，et al.A dynamic analysis of the plane crank and rocker mechanisms with clearances［J］.Bulletin of the JSME，1980，23（3）：446-452.

［7］周益君，关富玲.考虑杆件弹性和三维间隙铰机构动力学研究［J］.哈尔滨工业大学学报，2012，44（10）：122-127.

［8］MIEDEMA B，MANSOUR W M.Mechanical joints with clearance：a three⁃mode model［J］.Journal of Engineering for Industry，1976，98（4）：1319-1323.

［9］SOONG K，THOMPSON B.S.A theoretical and experimental investigation of the dynamic response of a slider⁃crank mechanism with radialclearance in the gudgeon⁃pin joint［J］.Journal of Mechanical Design，1990，112（2）：183-189.

［10］EARLES S W E，WU C L S.Motion analysis of a rigid⁃link mechanism with clearance at a bearing，using lagrangian mechanism and digital computation［C］／／Conference on Mechanisms.London：IME，1972：83-89.

［11］FURUHASHI T，MORITA N，MATSUURA M.Research on dynamics of four⁃bar linkage with clearances at turning pairs（including four reports）［J］.Bulletin of the FSME，1978，21（3）：518-523.

［12］白争锋，赵阳，赵志刚.考虑运动副间隙的机构动态特性研究［J］.振动与冲击，2011，31（11）：17-41.

［13］白争锋，赵阳，田浩.含铰间间隙太阳帆板展开动力学仿真［J］.哈尔滨工业大学学报，2009，41（3）：17-41.

［14］TSAI M J，LAI T H.Accuracy analysis of a multi⁃loop linkage with joint clearances［J］.Mechanism and Machine Theory，2008，43（9）：1141-1157.

［15］刘霞，王三民，单宁.基于杆长误差的飞行器货舱门锁机构运动精度分析研究［J］.机械科学与技术，2012，31（11）：1820-1830.

［16］TSAI M J，LAI T S.Door closing force analysis of Watt⁃I Type hinge with joint clearance［C］／／Proceedings of 12th IFToMM World Congress.Besançon：Elsevier，2007：18-21.

［17］孟祥志，蔡光起，胡明，等.三杆混联数控机床的动力学［J］.机械工程学报，2006，42（6）：113-119.

［18］DUPAC M，BEALE D G.Dynamic analysis ofa flexible linkage mechanism with cracks and clearance［J］.Mechanism and Machine Theory，2010，45（12）：1909-1923.

［19］MURRAY R M，LI Zexiang，SASTRY S S.A mathematical introduction to robotic manipulation［M］.Boca Raton：CRC Press，1994：61-73.

（编辑杨 波）

Effect of kinematic pairs clearance on dynamic characteristics of multi⁃linkage lock mechanisms

ZHI Changjian，WANG Sanmin，SUN Yuantao
（School of Mechanical Engineering，Northwestern Polytechnical University，710072 Xi′an，China）

To reduce the probability of aircraft cargo door opened accidently caused by abnormal stress，the dynamic characteristics of multi⁃linkage lock mechanisms with kinematic pairs clearance are studied in detail.The equivalent joint clearance link（the length is e）is used to describe the influence of kinematic pairs clearance.Meanwhile，the dynamic analysis model of multi⁃linkage lock mechanisms is built based on the Lagrange kinetic equation and the screw theory，and the procedures programmed by MATLAB are used to solve and analysis the model.Results indicate that the kinematic pairs clearance has a bigger influence on angular velocity of the rod，angular acceleration of the rod，driving moment and hinge binding kinematic，and the greatest influence appears near the singular configuration.While e is 10μm，its impact on dynamics of the multi⁃linkage lock mechanisms is small，however while e is 100μm，the impact is enhanced obviously.

kinematic pairs clearance；multi⁃linkage lock mechanisms；screw theory；equivalent joint clearance link；dynamic characteristics

TH122

A

0367-6234（2014）08-0102-05

2013-07-09.

国家自然科学基金资助项目（51175422）.

智常建（1984—），男，博士研究生；

王三民（1961—），男，教授，博士生导师.

王三民，wangsami＠nwpu.edu.cn.