牛顿法在新的仿射逆变条件下的半局部收敛性分析

王海波， 秦 梅

（上海理工大学理学院，上海 200093）

牛顿法在新的仿射逆变条件下的半局部收敛性分析

王海波， 秦 梅

（上海理工大学理学院，上海 200093）

非线性方程及非线性方程组的数值求解一直是计算数学所关注的问题，公认的经典算法是牛顿法，对于它的局部收敛性已有很多研究.在经典牛顿法的半局部收敛Kantorovich定理的基础上引入仿射逆变性，研究了牛顿法在仿射逆变Lipschitz条件和仿射逆变Holder条件下的半局部收敛性.简化了牛顿法的收敛行为，得到了相应的半局部收敛性定理及误差估计.推广并改进了相关文献的结果，表明了该方法的有效性.

牛顿法；仿射逆变Lipschitz条件；仿射逆变Holder条件；半局部收敛性

考虑非线性方程组其中F：Rn→Rn是连续可微函数.求解该非线性方程组的近似解是一个很重要的问题，因为大量的不同类型的实际问题都可以归结为非线性方程的求解，如常微分或偏微分方程边值问题、积分方程、极小化问题等［1-7］.为此，研究非线性方程组的求解算法具有重要的实际意义.

目前，牛顿法是求解非线性方程组（1）的最有效方法之一.其迭代格式为迭代法的收敛性已经成为研究的一个核心问题.一般情况下，收敛性分析有以下三种类型［2］：局部收敛性、半局部收敛性和全局收敛性.本文主要研究牛顿法在仿射逆变条件下的半局部收敛性.半局部收敛性是在不知方程解x*存在的情况下，根据F在某一初始点x0的局部条件来研究有关的收敛性质.

关于半局部收敛性的最著名的结果是Newton-Kantorovich定理［5］，该定理在理论和应用上相当重要，也是解方程算法现代研究的起点.很多研究学者对Kantorovich定理条件进行改进，得到了不少好的半局部收敛性结果.Deuflhard［8-9］首先将仿射不变性引入到牛顿法中，提出牛顿法的仿射不变性理论，而后由Hohmann得到进一步拓展.Nashed等［10］研究了阻尼牛顿法在仿射逆变条件下的局部收敛性.白中治［11］给出了不精确牛顿法在仿射协变条件下的不精确牛顿法的半局部收敛性.徐秀斌［12］研究了在弱Lipschitz条件下Halley方法的半局部收敛性.

大多数文献是在假设满足仿射协变条件下研究牛顿法的收敛性，而对仿射逆变条件下的研究较少.本文将结合文献［9］的思想，主要研究加入新的仿射逆变性后的牛顿法的半局部收敛性，并在更弱的仿射逆变条件下牛顿法的半局部收敛性得到了更一般的结果.

1 预备知识

考虑非线性方程组F（x）=0.其中F：D⊂X→Y的连续可微映射，X和Y为Banach空间.普通牛顿法对F（x）=0进行求解时，实际是求解线性方程组

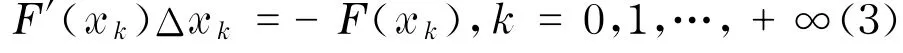
求得上述方程组的精确解Δxk后，由xk+1=xk+ Δxk进行校正.显然，普通牛顿法使非线性方程组F（x）=0的求解问题变成线性方程组（3）来解决.

上面的线性方程组（3）的可解性的必要条件是：对所有的x∈D，雅克比矩阵F′（x）是可逆的.在经典的收敛定理中通常要求F′（x）-1存在且有界，即

从实际计算的角度看，除了一些简单的例子外，理论上的量β是不容易得到的.然而，

是可取的.

研究上面的牛顿迭代的收敛性质，F（x）的二次导数信息是必要的.有大量的文献对式（4）进行弱化，Kelley［3］将其弱化为F＇的Lipschitz连续：存在一个常数L＞0，使得

经典的收敛性定理的假设条件都是式（4）、（5）、（6）的组合.现给出2个重要的收敛定理.

普通牛顿法缺乏仿射不变性.Hohmann在牛顿法中加入仿射逆变性，收到了很好的效果.相对于经典的牛顿法，利用仿射逆变性令收敛定理的证明更加简洁.为此，给出仿射映射的定义.

定义1 设F∈D⊂X→Y的映射，A是X到Y上的任意线性算子，对于任意的x，b∈D，称F（x）=A x+b为X上的仿射映射.

设A，B∈Rn×n是任意非奇异的n阶矩阵，考虑非线性系统的仿射变换

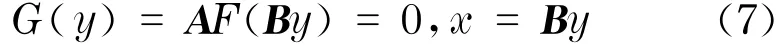
则将牛顿法应用到G（y）上可得

由于G′（yk）=A F′（xk）B和初始点y0=B-1x0，故对任意的k∈N，有xk=B yk.

很显然，他们仅仅是通过B的一个变换得到的.因此，有牛顿法产生的序列｛xk｝在仿射变换条件下具有不变性.

定义2 若固定F的像空间，即令A=I，则称G（y）=F（B y）=0，x=B y，B∈GL（n）为仿射逆变性.

对于这个问题，普通牛顿法推不出关于｛yk｝的迭代序列，但是可以导出关于残差｛F（xk）｝的序列，这与B的选择无关.另外，在经典的收敛定理中，F′（x）的Lipschitz连续是必要的.加入仿射逆变性后，将Lipschitz条件和‖F′（x）-1‖≤M结合得到仿射逆变Lipschitz条件

考虑到Lipschitz条件是Holder条件的特例，将Holder条件与‖F′（x）-1‖≤M结合得到仿射逆变Holder条件

显然，这两个条件满足仿射逆变性，因为对任意可逆线性算子B，若对非线性方程（1）作仿射逆变变换G（y）=F（By）=0，则

下面给出仿射逆变Lipschitz条件和仿射逆变Holder条件的定义.

定义3 （仿射逆变Lipschitz条件）设F：D⊂X→Y连续可微，对于任意的x，y∈D，如果对任意的v∈D有

则称为F′在D上满足仿射逆变Lipschitz条件.

定义4 （仿射逆变Holder条件）设F：D⊂X→Y连续可微，如果对于任意的v∈D有

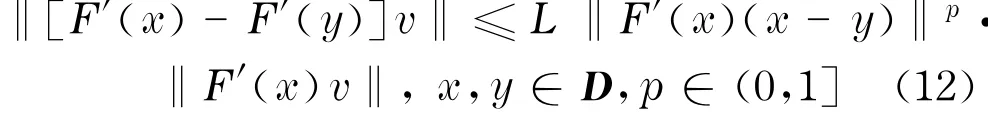
则称为F′在D上满足仿射逆变Holder条件.

在Kantorovich定理的基础上给出仿射Lipschitz条件半局部收敛性分析，并由此推出更弱的仿射逆变Holder条件下的半局部收敛性分析，后者是前者的推广.得到了牛顿法在仿射逆变条件下的更一般的结果.

2 牛顿法在新的仿射逆变条件下的半局部收敛性分析

讨论牛顿法的半局部收敛性，最著名的定理是康托洛维奇定理.

引理3 （康托洛维奇定理［5］）设F：D⊂Rn→Rn及初始近似x0满足下列条件：

引理4 （中值定理［5］）若映射F：D⊂Rn→Rn在开凸集D上可导，F′（x）在D上连续，则对任何x，y∈D，有

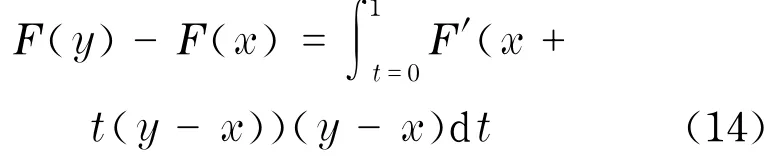
康托洛维奇定理有很大的理论价值，一方面是定理的收敛条件，另一方面就是定理的证明方法，为研究仿射逆变条件下牛顿法的半局部收敛性做了指导.在此基础上，在牛顿法中引入仿射逆变性，先研究牛顿法在仿射逆变Lipschitz条件下半局部收敛性.

定理1 （仿射逆变Lipschitz条件下半局部收敛性定理）设F：D→Rn是在D上的连续可微映射，D⊂Rn是一个开的凸集.F′（x）对任意x∈D均可逆，并设F′满足仿射逆变Lipschitz条件成立，即

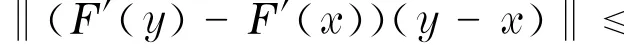
接下来在定理1的基础上研究比仿射逆变Lipschitz条件更弱条件下（仿射逆变Holder条件）的牛顿法的半局部收敛性.

定理2 （仿射逆变Holder条件下半局部收敛性定理） 设F：D→Rn是在D上的连续可微映射，D⊂Rn是一个开的凸集.F′（x）对任意x∈D均可逆，并设F′满足仿射逆变Holder条件成立，即p+1

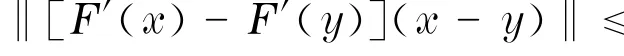
因此定理2是定理1的推广.需要注意的是，当水平集确定时，只要取其中任意一点作为初始迭代点便可以保证所产生的序列仍在水平集内且是收敛的.从而此结果推广并改进了经典的半局部收敛性定理.

3 结 论

主要研究了仿射逆变Lipschitz条件下牛顿法的半局部收敛性，并在此基础上给出了仿射逆变HolderF条件下牛顿法的半局部收敛性定理，得到了更一般的结果.由此可以得出结论：定理2是定理1的推广.此结果推广并改进了经典的半局部收敛性定理.

而对于牛顿法的高阶推广迭代算法，如Halley法和Chebyshev法是否能够建立仿射逆变条件下的收敛性，这一点目前还没有人做深入的探讨.一个关键的切入点是需要论证这些高阶算法是否具有仿射逆变性，如果满足该不变性，那么便可能可以建立相应的仿射逆变收敛结果.

［1］ Deuflhard P.Newton methods for nonlinear problems ［M］.北京：科学出版社，2006.

［2］ 袁亚湘.最优化理论与算法［M］.北京：科学出版社，1997.

［3］ Kelley C T.Solving nonlinear equations with Newton method［M］.Philadelphia：Society for Industrial& Applied Mathematics，2003.

［4］ Deuflhard P.Affine invariant adaptive Newton codes for discretized PDEs［J］.2002（10）：1-27.

［5］ 黄象鼎，等.非线性数值分析［M］.武汉：武汉大学出版社，2010.

［6］ 于淼，高岩.拟可微方程组牛顿法的二次收敛性［J］.上海理工大学学报，2009，31（4）：354-358.

［7］ 刘晶，高岩.求解一类无限维非光滑算子方程的光滑化牛顿法［J］.上海理工大学学报，2008，30（2）：167-170.

［8］ Deuflhard P，Heindl G.Affine invariant convergence theorems for Newton’s method and extensions to related methods［J］.SIAM Numer Anal，1979，16（1）：1-10.

［9］ Deuflhard P.Newton methods for nonlinear problems：affine invariance and adaptive algorithms［M］.Berlin：Springer-Verlag，2004.

［10］ Nashed M Z，Chen X.On the semilocal convergence of damped Newton method［J］.Applied Mathematics and Computation，2012（219）：2808-2824.

［11］ 白中治.不精确Newton法与Broyden法的仿射不变性［J］.电子科技大学学报，1994，23（5）：535-537.

［12］ Xu X B，Ling Y H.Semi-local convergence for Halley’s method under weak Lipschitz condition［J］. Applied Mathematics and Computation，2009，215（8）：3057-3067.

（编辑：董 伟）

Semi-local Convergence for Newton Method under New Affine Contravariant Conditions

WANGHai-bo， QINMei
（College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

Numerical solutions for nonlinear equations and systems of nonlinear equations are always appealing greatly to people.There are many papers discussing the local convergence of Newton method，a universally acknowledged classical algorithm.In the paper，on the basis of the Kantorovich theorem about the classic semi-local convergence of Newton method，affine contravariant conditions were introduced and the semi-local convergence of Newton method under affine contravariant Lipschitz conditions and affine contravariant Holder conditions was analysed. The convergence behavior of Newton method was simplified.The semi-local convergence theorems were presented and the estimations of the iterative residual were obtained.The results extend and improve the results in the related paper，which show that the method is efficient.

Newton method；affine contravariant Lipschitz conditions；affine contravariant Holder conditions；semi-local convergence

O 241文献标示码：A

1007-6735（2014）05-0429-05

10.13255／j.cnki.jusst.2014.05.004

2013-09-04

王海波（1987-），男，硕士研究生.研究方向：计算数学.E-mail：nunywanghaibo＠126.com

秦 梅（1975-），女，副教授.研究方向：计算数学.E-mail：qinmay2012＠sina.com