灾害应急状态终止的随机决策与仿真
黄 星,王绍玉,2
灾害应急状态终止的随机决策与仿真
黄 星1,王绍玉1,2
(1.哈尔滨工业大学管理学院,150001哈尔滨;2.哈尔滨工业大学建筑学院,150001哈尔滨)
为确定灾害应急状态终止时间,通过对应急状态终止状态影响因素的分析,将应急状态分为应急紧张状态和应急稳定状态2种,针对各状态指标先期的统计数据,结合马尔科夫过程,寻找出应急状态进入稳态概率分布的最大时间N,然后运用最优停止理论在N中寻找出应急状态终止的最优时间,并建立应急状态终止的马氏链决策-最优停止理论模型.基于马氏链的灾害应急状态终止模型能较准确地对应急状态终止时间进行量化决策,且计算简便,易于计算机实现,具有较强的可操作性,所提出的模型为掌握应急所处状态和对应急状态终止时间进行决策提供了理论支持.
应急状态终止;马氏链模型;稳态分布;最优停止;状态概率
应急状态的终止属于应急响应机制的最后一环,也是应急管理从应急的紧张状态转为应急稳定状态并进入常态的关键,过早或过晚结束都可能导致严重的次生灾害和巨大的财物浪费.
目前,应急管理机制的研究成果主要集中于以下几个方面:一是对应急管理机制基本框架的研究,闪淳昌等[1]以应急管理全过程为主线,提出应急管理机制建设的20个具体内容;钟开斌[2]根据机制所体现的不同功能将应急机制划分为社会动员、恢复重建和灾害应急评估等9种机制;二是从不同方法上对单个机制进行大量研究,如CORRIVEAU[3]从信息流的角度对应急联动决策进行研究,FIEDRICH等[4]从应急物资动员机制的角度提出震后应急物资优化配置及响应模型,陈安等[5]基于有限情形的秘书问题.从以上文献来看,鲜有涉及应急状态终止问题,已有文献也是基于随机效益值为已知情况下寻找最优停止时间的,这对事中紧急救援决策的指导意义不大.本文从影响应急状态终止的多因素角度,运用马尔科夫决策和最优停止理论构建有限情形的应急状态终止模型,为应急管理决策提供方法支撑.
1 基于Markov的应急状态终止的最大停止时间决策
在马尔科夫过程中,给定系统的初始状态,如果把时间n看成“现在”,把时刻0,1,…,n-1看成过去,把时刻n+1看成“将来”,那么马尔科夫性说明,在已知系统“现在”所处状态条件下,系统“将来”到达某种状态的条件概率与“过去”所经历的状态无关,系统根据一定的概率分布在各个状态之间转移,“将来”的状态具有随机性,这跟应急系统因应急能力和不确定因素制约造成应急效率高低的随机性类似[6-8].
1.1 应急状态衡量指标
一般来讲,应急状态衡量指标主要从灾害本身控制、需求提供和人员临时安置(包括陆续救出的埋压伤亡人员的安置)、应急成本和社会影响因素等方面提取.其中,社会影响因素(如公众恐慌度)一般持续时间较长,很难定量,而且在有限的应急期间恐慌度变动除受灾害等级、救援效率等因素影响之外,主要是通过长期的自我调节和心理援助等方式予以消除,故本文不将社会因素作为应急状态衡量指标;根据灾害应急的弱经济性特点,应急成本也不宜作为影响应急状态衡量指标.综上,本文将灾害控制、应急物资需求满足和灾区人员临时安置作为灾害应急状态的衡量指标.
在应急状态发生概率计算方法上,灾害控制指标是指灾害发生后导致灾害影响范围或损失的继续蔓延或扩大,可根据前期统计数据或参照案例将单位时间发生的情况按一定规则划分为2个等级(应急紧张状态和应急稳定状态),并分别统计每个状态等级上发生的频率,如洪灾,可先将单位时间内扩大的受灾面积划分为2个等级,然后把每个等级上出现的频率作为转移概率,没发生计为零;同理,疫情灾害可按感染人数变动来计量,地震灾害按灾后发生的余震次数来计量;应急物资需求满足是指每次应急物资供给量与需求量的比率,其状态发生概率的计算方法与灾害控制指标类似;灾区人员临时安置指标主要是对比单位时间实际安置人数和计划安置人数,将比率按不同状态划分为2个等级,并将每个等级上统计出的频率作为状态转移概率.
1.2 基本假设
假设2 设应急紧张状态的概率为P(X= 1),应急稳定状态的概率为P(X=2).每个状态衡量指标的初始状态有2种:应急紧张状态和应急稳定状态,而3个指标的应急初始状态应是应急紧张状态和应急稳定状态的排列组合.
假设3 设灾害控制在2种状态之间的一步转移概率元素分别为ε11、1-ε11和ε21、1-ε21,应急物资需求满足在2种状态之间的一步转移概率元素分别为η11、1-η11和η21、1-η21,灾区人员临时安置在2种状态之间的一步转移概率元素分别为μ11、1-μ11和μ21、1-μ21.
1.3 应急状态终止的最大停止时间
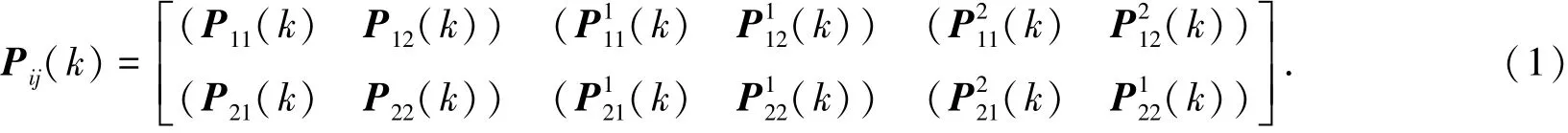
其中,
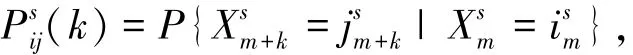
假设应急系统的初始状态经过n单位时间段的转移后的状态向量为
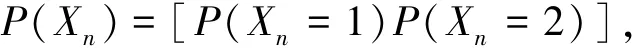
由C-K方程有:

故经n阶段后,应急状态的概率分布可由初始状态和一步转移概率算出.由以上所给条件可推出P(Xn)的分布函数表达式:
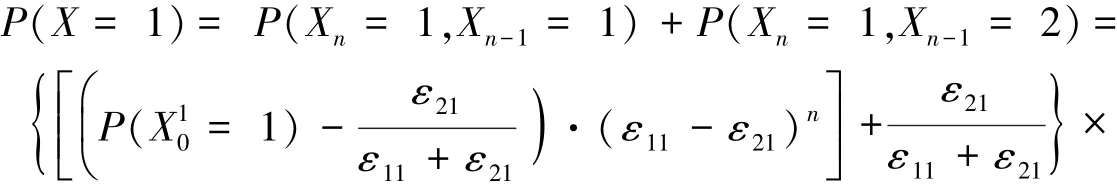
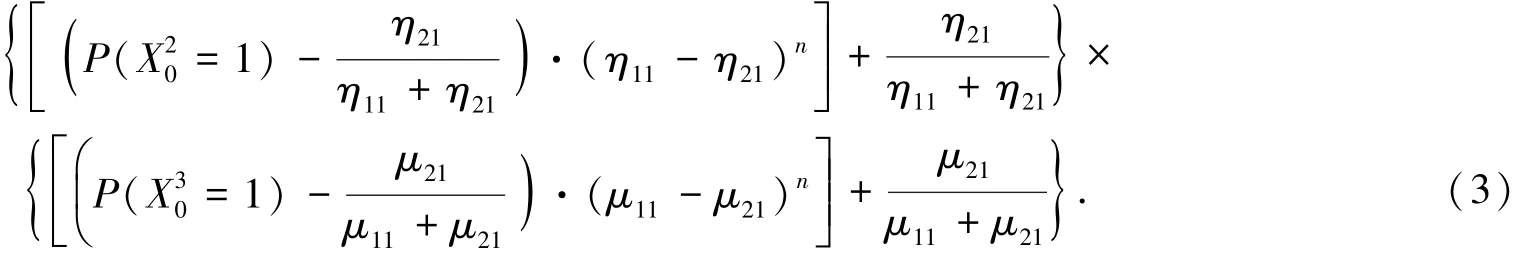
同理

重大灾害发生后,应急指挥中心采取紧急救援的概率为百分之百,故可设定应急初始状态的概率分布为P(X0)=[(111)(000)],则有

式(5)为随机过程X经n单位时间后应急状态的概率向量,经过若干个有限单位时间的概率转移后,应急状态处于1或2的概率将趋于稳态,且稳态概率与初始状态无关.设稳定状态下的概率为π,则当应急系统达到稳定状态时,有条件立,则每个衡量指标达到稳定状态后的稳定概率为:

整个应急系统达到稳态时的状态向量为:
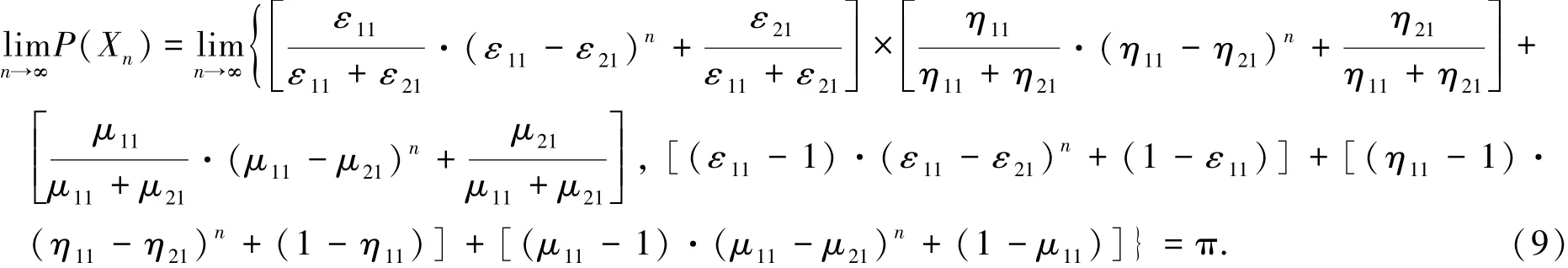
根据灾害应急特点,当应急状态达到稳定状态,说明灾区应急工作达到了常规计划状态,而常规计划状态也表明应急状态结束,否则灾害应急仍会处于相对紧张状态,故应急系统达到稳态时的时间可看作灾害最大计划停止时间N,而灾害应急的最优停止时间应包括在N内.
2 最优停止时间的确定
2.1 基本假设
假设2[9-10]设一列随机变量,称之为报酬函数序列.对每一个n,Xn是Fn可测的,记Xn∈Fn,称{Xn,Fn}为随机序列.称取值为{1,2,…,+∞}的随机变量t为停时,若有∀n,{ω:t=n}∈Fn成立,还有P(t<∞)=1,则称t为停止规则,全体停时记为¯H,全体停止规则记为H.
假设3 如果序贯地观察到随机变量y1,y2,…,yn,报酬函数序列Xn与y1,y2,…,yn对应,且
2.2 应急效益衡量指标及最优标准的提出
通常来看,时间和成本是影响灾害应急效益的关键指标,设在灾害应急中,每天都有应急物资提供,每天都有应急成本发生.应急时间效益指标主要突出于应急物资的及时提供上,当应急物资需求提出后,应急系统快速高效地提供所需应急物资,这是保证灾害应急任务顺利完成的决定性指标之一,故应急物资平均满足时间(Mt)是其衡量指标之一,平均应急物资满足时间越短,时间效益值越大;应急成本效益指标主要由应急物资运输成本和应急物资成本组成,数据统计时,按每天发生成本求和即可,故应急成本(C)也应是关键衡量指标(见表1),应急成本越小,应急成本效益值越大.由于Mt、C指标在整个灾害应急中具有相对独立性,很难用一个综合指标来统一计量,只能根据最优停止规则分别决策,为了简便这里重点介绍Mt指标的最优停止方法,在最后决策时只需比较两指标分别决策时的最优停止时间的大小,选取最大的停止时间作为应急状态终止的最优停止时间,因为只有这两个指标全部达到最优后才可以结束应急状态,否则,灾害应急效益不能达到最优.

表1 应急状态终止最优停止决策的衡量指标
记M(1),M(2),…,M(N)为M在N天内取值的一个降序排列,属于绝对排名,其中M(1)最大,M(N)最小;这个绝对排名只有N结束后才可以得到,在进行随机决策时并不能事先知道这个绝对排名,做决策时只能对已过去的n天进行排名,这样一来每次决策时会得到一列相对排名,也就是说,每次随机决策会得到一个1,2,…,N的任意排列,随机决策的目的就是既要找到效益值最大且排名靠前的概率最大.这样一来,应急状态终止的最优停止问题就转化为求解以下两个标准的问题:一是使应急状态终止时间选在M值最大的概率最大;二是使应急状态终止时间选在M值绝对排名的平均值最小.
2.3 两个标准停止规则的构造
令Ω={(a1,a2,…,aN)},其中(a1,a2,…,aN)是(1,2,…,N)的一个排列;yn=(a1,a2,…,an),an的相对名次为yn中小于an的个数,设Fn= σ(y1,y2,…,yn).对标准1,取报酬序列:
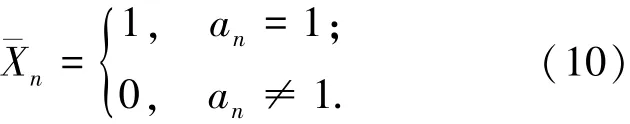
但它不满足Fn可测的要求,令
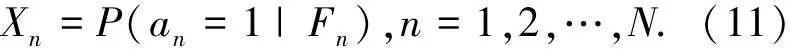
对任意停止规则t有:

其中,P(at=1)表示选择停止规则t时,M恰好排名第一的概率,也就是M最大的概率,于是{Xn,Fn}的最优停止问题的最优规则应为
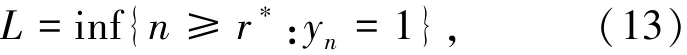
其中

满足此条件的最小r也就是r∗的取值,符合式(13)的r∗后第一个最大的M值所对应的时间t即为应急最优终止时间[11-12].为了计算简便,也可以通过对式(13)求极限求得r∗,由式(14)有下式成立:
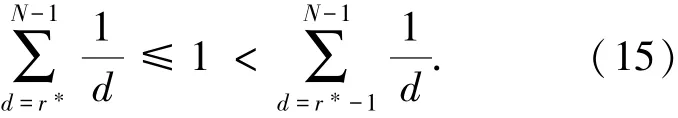
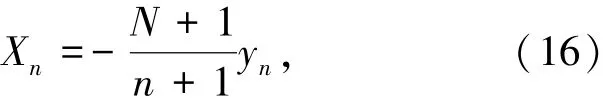
最优规则为
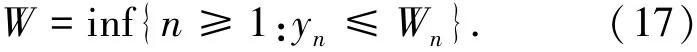
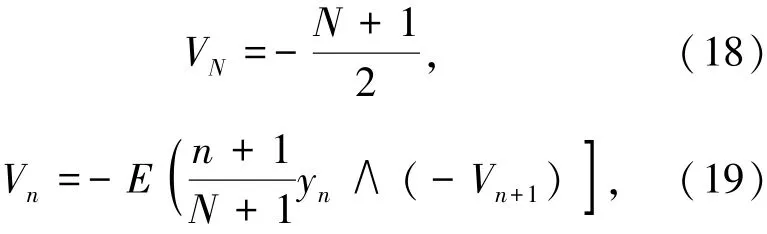
其中1≤n≤N-1.
对标准2的算法可设计为:
Input:N

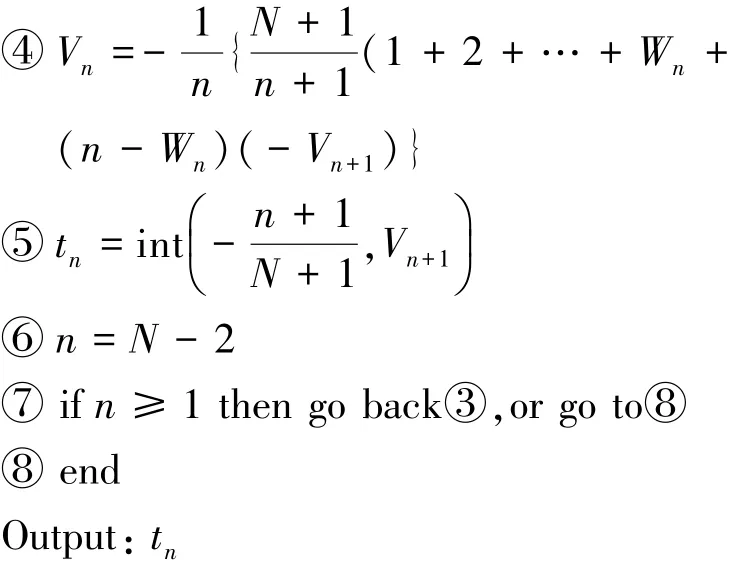
2.4 应急状态终止的最优时间决策
在应急状态终止决策中,上述2个标准的最优规则既可以单独使用,也可以相互补充,单独用标准1时,在确定r∗值后,立即知道int[r∗]天前不宜终止,只有在int[r∗]后第1次出现最大时间效益值M所对应的时间t时,才有理由终止应急状态,这个t的确切值只有在事后才能明确,这对事后灾害应急评估有较大作用,但对应急物资需求预测和对灾害中后期进行统筹安排的指导作用不大;因此,实践中,在知道了N和r∗值后,应急状态终止时间的决策范围已经大大缩小了,这时可采取案例验证的方法估计出int[r∗]后第1次出现最大M值出现的时间,也可以取(int[r∗],N)∩(a,b)交集的时间区间,记为(c,d),然后取c,d的均值作为最优终止时间.同理,按照以上决策方法,可决策出成本效益的最优停止时间.
3 仿真算例
现以2008年“5·12”汶川大地震部分重灾区为例.实例仿真分为2个阶段:一阶段用马氏链模型寻找应急状态达到稳定状态时的最大应急状态终止时间点N,规定初始阶段以每5 d为1单位.在指标状态划分上,“灾害控制指标”主要统计从5月13日到5月17日的余震次数,其仿真数据见表2,并根据1980年编制的《中国地震烈度表》中所列举的不同地震烈度的强弱影响,规定每日发生2次5度以上地震和1次6度以上地震为应急紧张状态,其余为应急稳定状态;“应急物资需求满足指标”主要统计初始阶段每次应急物资及时提供量与需求量的比率,为了简化数据收集难度,这里选用最能影响应急状态的医用物资作为仿真数据,并规定满足率平均为75%以下为应急紧张状态,满足率平均为76%以上为应急稳定状态,在实际地震救援中,这个规定是比较合理的,仿真数据见表3;“灾区人员临时安置指标”主要统计初始阶段计划安置人数与实际安置人数的比率(包括当天救出的伤亡人员的安置),规定84%以下为应急紧张状态,85%以上为应急稳定状态,仿真数据见表4;二阶段是求解最优终止时间,这阶段只需根据N值按两个标准的最优规则求解即可.
3.1 应急状态的稳态随机分布
根据表2~4数据,计算各状态指标在初始阶段的频率,得到应急状态的一步转移概率矩阵向量:


表2 汶川地震5月13日-17日余震统计
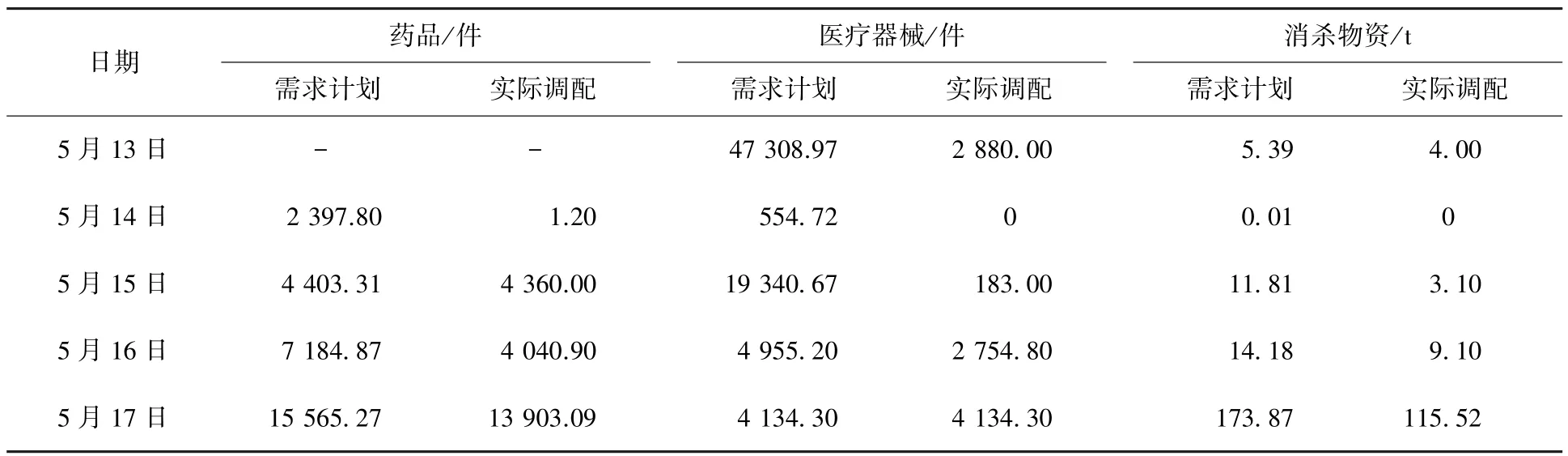
表3 汶川地震初始阶段医用物资供需统计
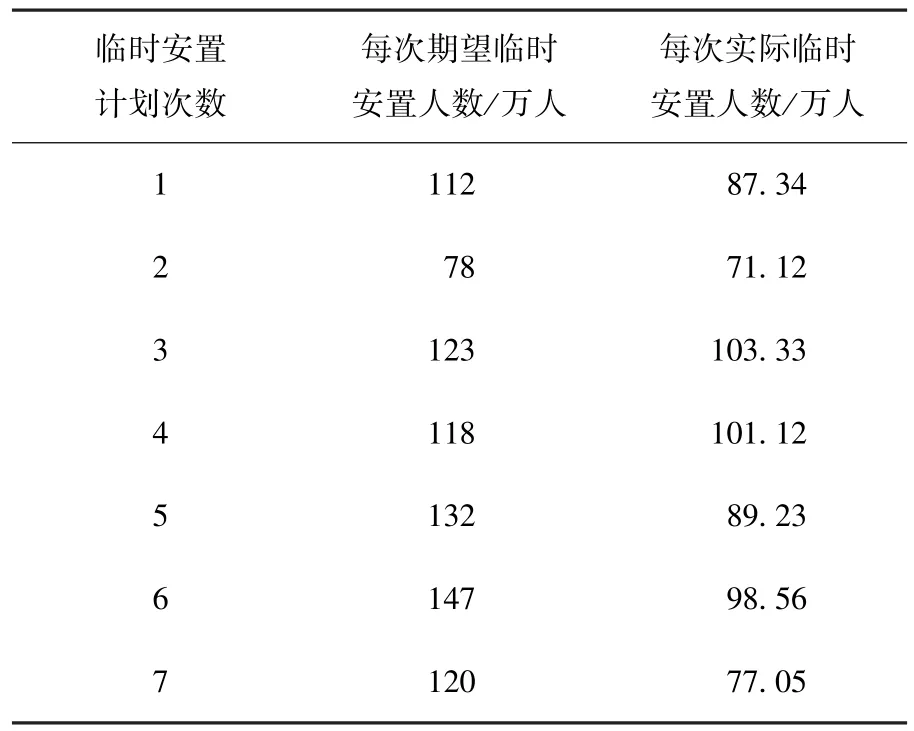
表4 汶川地震初始阶段灾区临时人员安置情况
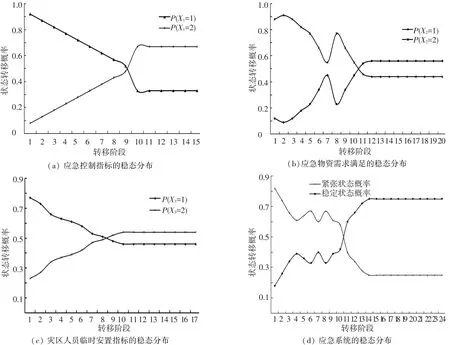
图1 应急状态指标和应急系统的概率转移分布
由前面式(6)~(8)可以分别得出各衡量指标状态转移分布,见图1(a)~(c).图1(a)为灾害控制指标的概率转移分布,状态达到稳定分布后P(X1=1)=0.33,P(X1=2)=0.67,历经11个单位时间段的转移,共55 d;图1(b)为应急物资需求满足指标的概率转移分布,应急物资需求满足指标状态达到稳定分布后P(X2=1)=0.44,P(X2=2)=0.56,历经13个单位时间段的转移,共65 d;图1(c)为灾区人员临时安置指标的概率转移分布,灾区人员临时安置指标状态达到稳定分布后P(X3=1)=0.46,P(X3=1)=0.54,历经11个单位时间段的转移,共55 d.3个状态指标中,应急物资需求满足达到稳定分布的时间较长,为加快应急状态终止速度,需重点从提高应急物资筹集与配送能力入手,但单个指标达到稳态后不能作为应急系统的最大计划停止时间,只有应急系统的状态达到一个相对静止的稳态后才可以确定应急状态终止的最大计划时间N,故根据式(9)得到图1(d)所示的应急系统的状态转移概率分布曲线,从图1(d)可知,应急系统历经15个单位时间段的转移后,应急紧张状态和应急稳定状态的概率分布呈现稳态分布,此时P(Xn=1)= 0.25,P(Xn=2)=0.75,最大应急计划停止时间N=75.
3.2 最优停时决策
1)根据标准1,在前27 d不能做出应急状态终止决策,只有在27 d后出现最大的时间效益值M(应急物资平均满足时间Mt最小)的第1 d(l)应急状态才可以终止,此时的M值相对于已经发生天数是最大值,并非绝对排名,故选取27 d后第1 d出现最大M值时终止的概率最大为0.276.
2)根据标准2算法设置程序语言,输出表5的结果.由表5,tn取值为1所对应的时间序列为{22,23,…,37},说明应急状态终止的最优停止时间应选择在(a,b)=(22,37)之间,此区间中排名最大的M所对应的时间点即为最优终止时间;前21 d中所有tn取值为0,说明前21 d不应终止应急状态.
3)应急状态终止决策.由标准1求出最优停止时间的关键变量为r∗=27.59,表明前27 d不应做出应急状态终止决策,由标准2求出的最优停止时间范围为(a,b)=(22,37),表明应急状态终止时间应在此范围内选择.决策时,标准2可作为标准1的验证,两种标准可单独使用,但无论采用哪种标准进行决策,都需要寻找出第1次出现的最大时间效益值,因为事前并不知道每天的效益值,故只能通过不断缩小时间范围来提高决策的准确度,在方法上可综合标准1和标准2的结论,取(int[r∗],N)∩(a,b)交集,记为(c,d),则有(c,d)=(27,37),这样,可进一步缩小决策范围;理论上,只要在此区间找出第1次出现的最大效益值,则所对应的时间就可大致确定为应急状态终止时间,在实践中,可把区间的中间点确定为应急状态终止时间.同理,可决策出成本效益的最优停止时间.如果采用两个衡量指标分别决策的最优停止时间不同,一般应以时间效益指标决策结果为准,这符合灾害应急特点.

表5 Vn和tn输出情况
4 结 语
运用马氏链决策过程对应急状态终止的最大计划停止时间N进行了研究.将最优停止理论引入到应急状态终止决策中,提出两类求解最优停止时间的标准和方法,为在(0,N)寻找最优停止时间提供保证,并从灾害应急的时间效益和成本效益的角度构建应急状态终止的最优停止模型,有效地将应急状态终止时间的决策范围大大缩小.影响应急状态终止的指标很多,本文只从易于统计的几个指标入手,这样会降低灾害应急状态终止决策的准确性,而且在最优停止理论的引入中只从单因素的角度构建理论模型,模型运行结果只能决策出最优停止时间的关键变量,不能决策出关键变量后第1次出现最大效益值的时间,下一步研究需配合精度较高的预测手段实现应急状态终止更为有效的决策.
[1]闪淳昌,周玲,钟开斌.对我国应急管理机制的总体思考[J].国家行政学院学报,2011,46(1):8-12.
[2]钟开斌.应急管理机制辨析[J].中国减灾,2008,35(4):30-31.
[3]CORRIVEAU G M.A cross-jurisdiction and multi-agency information modelforemergencymanagement[D]. Manitoba:University of Manitoba,2000,35(6):223-231.
[4]FIEDRICH F,GEHBANER F,RICKERS U.Optimized resourceallocationforemergencyresponseafter earthquake disasters[J].SafetyScience,2000,35(1/2/3):41-57.
[5]陈安,武艳南.基于最优停止理论的应急状态终止机制设计[J].中国管理科学,2010,18(4):173-182.
[6]CHEN W H,GUAN Z H.Delay-dependent output feedback stabilization of Markov jump systems with time delay[J].IEEProceedings-ControlTheoryand Applications,2004,151(5):561-566.
[7]LI Hongyi,CHEN Bing,ZHOU Q,et al.Robust stability for uncertain delayed fuzzy Hopfield neural networks with Markov jumping parameters[J].IEEE Transactions on Systems,2009,39(1):94-102.
[8]MAO Z,JIANG B,SHI P.H∞fault detection filter design for network control system model by discrete Markov jump system[J].IET Control Theory and Applications,2007,1(5):1336-1343.
[9]金治明.最优停止理论及其应用[M].长沙:国防科技大学出版社,1995:4-29.
[10]THOMAS J L.Optimal stopping with sampling cost:the secretary problem[J].Ann Probability,1981,9(1): 167-172.
[11]YI D Y.From optimal stopping problems over tree sets to optimal stopping problems over partially ordered sets[J].Journal of Mathematical Research&Exposition,1998,18(1):30-32.
[12]CHE Zhuming,JIN Zhiming.TI-Kth choice problem[J].SO-National University of Defense Technology Journal,1995,17(4):143-147.
[13]徐健康,邓兴光,李华,等.汶川地震四川省医用物资保障工作情况[J].中国循证医学杂志,2008,8(11): 905-912.
(编辑 赵丽莹)
Random decision and simulation for the state termination of disaster emergency
HUANG Xing1,WANG Shaoyu1,2
(1.School of Management,Harbin Institute of Technology,150001 Harbin,China;2.School of Architecture,Harbin Institute of Technology,150001 Harbin,China)
To determine the stop time of disaster emergency,the states of emergency were divided into two kinds of states,including emergency tension state and emergency stationary state after analyzing the influence factors of emergency termination states.Firstly,the maximum time N was found out by Markov decision model after the emergency state going into the stable phase,and then the optimal stop theory was used to solve the question of the emergency termination to find the most optimal termination time during the N,finally,the Markov chain's decision model of emergency state termination was established,which could accurately solve the question of the quantification decision of the end time of emergency state,and the calculation was simple. Markov model provided the theory support for emergency termination decision.
emergency state termination;Markov chain model;steady state distribution;the optimal stop;state probability
O232
A
0367-6234(2014)04-0013-07
2012-11-07.
国家自然科学基金资助项目(71372091).
黄 星(1979—),男,博士研究生;王绍玉(1956—),男,教授,博士生导师.
黄 星,huangxing6213@126.com.

