识别含水层参数的单纯形-混沌优化算法

袁 华，张玉海

（长安大学 理学院，陕西 西安 710064）

导水系数和储水系数等含水层参数在进行地下水资源评价时是非常重要的参数.获得含水层参数的主要方法之一是分析非稳定流抽水试验数据.泰斯公式[1]形式简单，又能反映在抽水过程中含水层水位的变化规律，故是分析非稳定流抽水试验数据、识别含水层参数的基本公式.目前，采用泰斯公式确定含水层参数的方法主要有：标准曲线配线法[1]、改进直线图解法[2]、Jacob直线图解法、非线性最小二乘法[3]等.在实际应用中，这些方法都有一些局限性.为了克服上述方法存在的局限性，学者已将模拟退火法[4]和混沌序列优化算法[5]等智能优化算法应用于求解含水层参数函数优化问题，且取得了较为满意的结果.

单独采用混沌优化算法求解含水层参数问题时搜索速度较慢.鉴于此，文中以泰斯公式为基础，采用在局部区域搜索性能较好的单纯形算法和在全局搜索性能良好的混沌优化算法结合的单纯形-混沌优化算法识别含水层参数.通过数值实验验证文中算法计算结果的可靠性，分析待求含水层参数初始取值范围和算法控制条件对算法收敛性的影响.

1 单纯形-混沌优化算法（CSM）

混沌序列搜索[5（]CM）因为混沌序列的遍历性而能够避免陷入局部最优，但在最优点附近搜索较慢；单纯形算法在局部搜索速度较快，但易陷入局部最优解，且对参数初值依赖性较强.鉴于此，文中采用这两种算法的结合，即单纯形-混沌优化算法.算法的具体步骤如下：

Step1利用Logistic映射产生混沌序列；

Step3进行混沌粗搜索，当 f∗＜ε1或k大于粗搜索次数，停止粗搜索；

Step4利用式（1）缩小解空间，其中，λ=0.618；

Step5利用单纯形法进行搜索[6]；

Step6如果abs(y)＜ε2或k1大于外循环次数，计算停止，否则转到Step1.

2 含水层参数识别问题

式中：sj表示第 j时刻的水位降深，L、计算公式参考文献[1]，其中一些参数的取值参考文献[7]；s0j表示抽水开始后第 j时刻观测到的实际水位降深值，L、θ为待估参数向量；j=1, 2, …, N为抽水试验过程中观测时间的序列号.对于问题（2），设含水层的导水系数T为θ1，储水系数 μ为θ2.

应用文中算法时，要求待估参数值使水位降深计算值与观测值间的离差平方和的均值达到极小，即

3 数值实验数据与结果分析

3.1 实验数据

采用文献[8]中实际抽水试验数据进行数值实验.在无限边界含水层条件下，抽水开始后距抽水主井30.48 m处观测孔中水头降深的观测数据见文献[8]，试验中抽水流量为0.0769 m3/s，抽水持续时间800 min.

3.2 结果分析

在无限含水层条件下，计算结果为T=2.8769 m2/min，μ=0.0666，目标函数值为ϕ=3.4620，从目标函数和与文献[2]中的结果对比，可知文中计算结果是可靠的.

表1和表2给出了取储水系数的上限为0.5，下限为0[5]，导水系数的下限为0时，算法各个控制条件下的单纯形搜索次数.从表中可以看出，随着导水系数倍数的增加，单纯形搜索次数虽有波动，但整体呈增加趋势，这个现象说明，待估参数的初始取值范围、粗搜索的次数和混沌序列长度对算法的收敛速度有一定的影响.但在整个实验过程中没有出现算法不收敛和解不唯一的情况，所以它们不影响算法最终的收敛性.可见，文中算法弥补了非线性最小二乘法在计算含水层参数过程中，计算结果和算法的收敛性依赖于参数初始输入值的不足之处.

文中算法的收敛性由单纯形算法的收敛性决定.一般混沌序列越长，粗搜索次数越多，越可能直接找到问题最优解.从表1、2可看出，当待估参数范围确定时，单纯形搜索次数随序列长度和粗搜索次数的增加呈减少趋势，最后趋于稳定.即在序列长度和粗搜索次数大于一定值时，它们对单纯形搜索次数影响较小，太长的序列长度和过多的粗搜索次数不会加速算法收敛，故它们的取值使算法不陷入局部最优即可.就文中算例而言，结合本文实验和参考文献[5]，混沌序列长度在200～600之间，粗搜索次数在2～10次之间为宜.

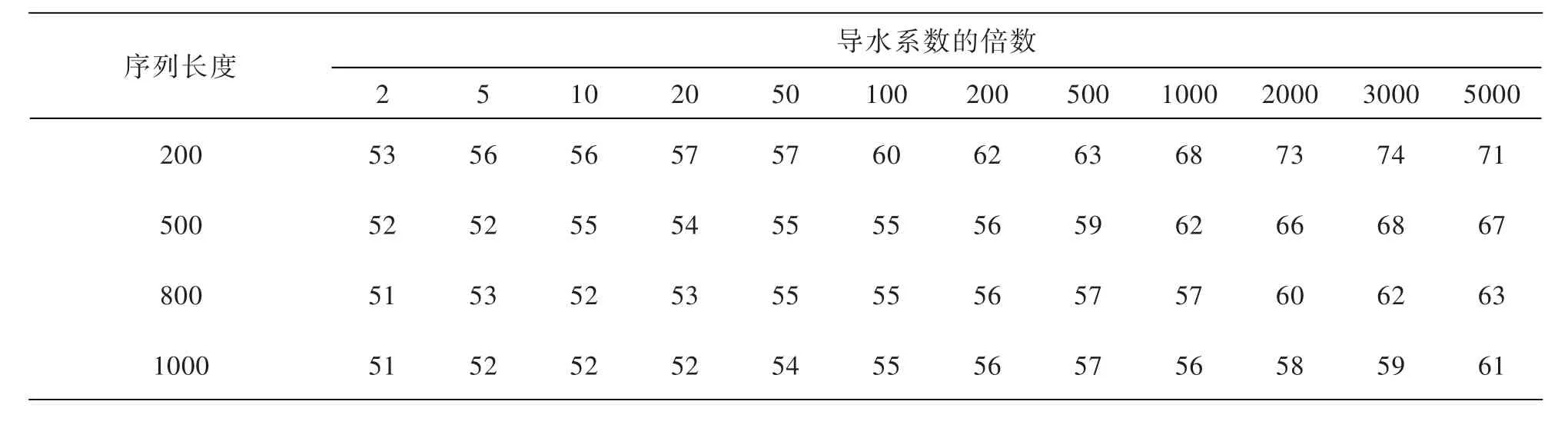
表1 粗搜索次数为2时细搜索次数与算法控制条件的关系

表2 粗搜索为5时细搜索次数与算法控制条件的关系

4 结语

通过以上分析讨论可知，单纯形-混沌优化算法能够有效地运用于分析抽水试验数据，识别含水层参数.数值实验结果表明：文中算法可以有效地应用于识别含水层参数，且计算结果是可靠的；待估参数初始取值范围对算法的收敛速度有一定的影响，但不影响算法最终的收敛性；就文中算例而言，混沌序列长度在200～600之间，粗搜索次数在2～10次为宜.简而言之，在分析抽水试验资料和识别含水层参数时单纯形-混沌优化算法是一种有效的方法.

[1]陈崇希，林敏.地下水动力学[M].武汉：中国地质大学出版社，1999：70-120.

[2]郭建青，周宏飞，李彦，等.分析非稳定流抽水试验数据的改进直线解析法[J].中国农村水利水电，2009（4）：18-21.

[3]齐学斌.非稳定流抽水试验参数的迭代算法及计算机模拟[J].水利学报，1995（5）：67-71，66.

[4]张娟娟，郭建青，韩淑敏，等.基于改进模拟退火算法反演水文地质参数[J].中国农村水利水电，2005（9）：8-11.

[5]郭建青，李彦，王洪胜，等.确定含水层参数的混沌序列优化算法[J].中国农村水利水电，2006（12）：26-29.

[6]张智星，孙春在.神经-模糊和软计算[M].西安：西安交通大学出版社，2000：131-135.

[7]Srivastava R.Implications of using approximation expressions for well function[J].Journal of Irrigation and Drainage Engineering,1995,121(6):459-462.

[8]U.S.Department of the Interior(USDI).Groundwater Manual[M].Washington D C:Bureau of Reclamation.Supt.of Documents,U.S.Govt.Printing Office,1977:119.