一种配电网对地电容精确测量新方法

程玉凯

（福建漳州电力公司，福建 漳州 363000）

随着配电网规模的扩大和电缆线路的大量应用，使得系统对地电容电流不断增大.过大的电容电流给配电网的安全稳定运行带来了很大的隐患，因此必须加以限制.目前对于电容电流的限制措施采用最多的是加装消弧线圈，利用消弧线圈提供感性电流来补偿系统对地电容电流，使得电容电流被限制在一个较低水平.而加装消弧线圈必然会额外增大电力系统运行和维护成本，因而对于本身对地电容电流较小的电力系统来说，没有必要装设消弧线圈；对于对地电容电流较大的电力系统来说，装设消弧线圈十分必要.以6 kV电网来说，《电力系统接地规程》规定，当电容电流大于20 A时，需要加装消弧线圈对电容电流抑制；反之，则不必装设消弧线圈[1-3].电容电流的大小与系统对地电容和系统频率有直接关系.电力系统频率一般来说波动不大（波动不超过±2%），因而要想得到某个系统电容电流的大小，需要知道系统对地电容的大小.测得的对地电容越精确，消弧线圈调节越有效，系统对地电容电流抑制效果越明显.因而，如何得到精确的对地电容值是抑制电容电流的关键所在.

本文基于单相接地故障消失后零序电压的衰减震荡频率与系统等效对地电容之间的关系提出了一种对地电容测量方法.文献[3]也提出过类似方法，其主要应用于中性点不接地系统，人为构造高阻接地相，通过测量经高阻接地电流预测金属性接地电流，但利用这种方法测得的单相接地电流与实际值之间存在一定误差，精确度不高.本文提出的对地电容测量方法只要准确测量零序电压周期就可以实现系统对地电容的精确测量.

1 电力系统故障等值结构图和等值电路图

一个简单的电力系统发生单相接地故障时的等值接线图如图1所示.

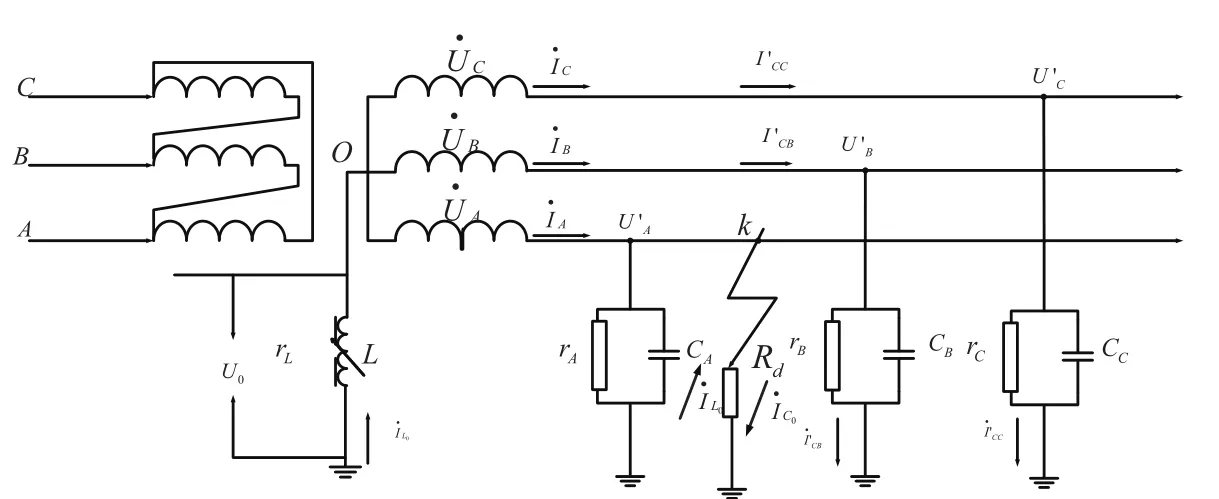
图1 谐振接地系统单相经过渡电阻接地接线图

为便于分析作如下假设：系统经过线路换位使得三相保持对称，即：CA=CB=CC=CO,rA=rB=rC=rO,利用戴维南定理将图1所示的等值接线图简化为如图2所示的等值电路图.

图2中，C表示三相对地等值电容，由式（1）可知，其值可表示为：表示三相对地泄露电阻，由式（2）可知，其值可表示为分别表示系统对地电容电流、消弧线圈输出电感电流和系统对地阻性电流，表示单相接地残流，表示零序电压，即消弧线圈两端的电压.若消弧线圈L和对地电容C在电源频率达到谐振状态，那么单相接地残流达到最小值，即

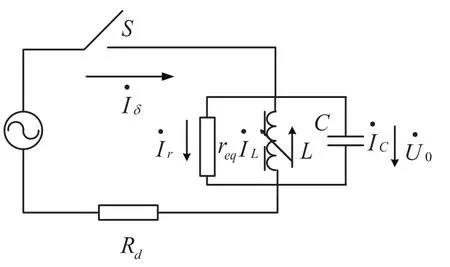
图2 单相接地等值电路图

当单相接地故障发生时，S由原来的开断状态变为闭合状态，对地电容和消弧线圈是一个充电过程，零序电压是一个递增的电压.经过一定时间后，零序电压达到稳定值，单相接地残流达到稳定值，其大小与消弧线圈与对地电容的合谐度有关[4-5].

2 单相接地故障消失后零序电压的表达式

单相接地故障消失时，图2中开关S由闭合状态变为断开状态，对地电容和消弧线圈放电，因而零序电压是一个衰减电压.下面分析单相接地故障消失后零序电压的表达式[6-8].单相接地故障消失后的等效电路如图3所示.

设零序电压初始值为

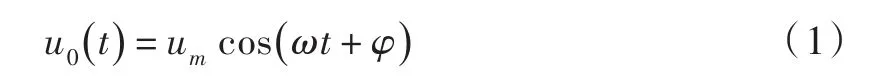
根据节点电流定律可得到

而

因此

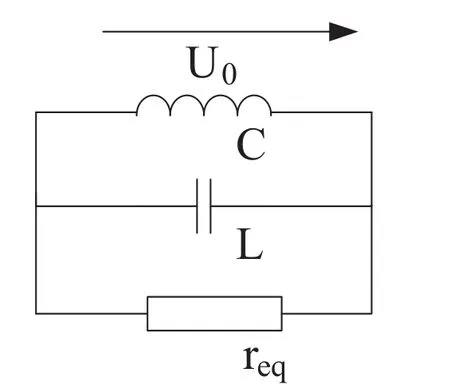
图3 单相接地故障消失后的等值电路图

两边求导整理得到

再将上式化为

令

得到式（4）的齐次方程为：

设消弧线圈与对地电容在频率为ω1时达到谐振状态，即

所以

因而方程有两个复数根.设方程的两个复数根

此时其初始条件为：

将式（14）代入通解得到：

整理得到

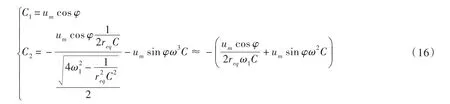
方程通解可化为：为两常数.

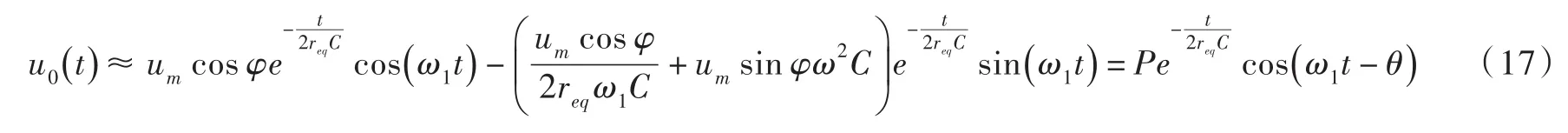
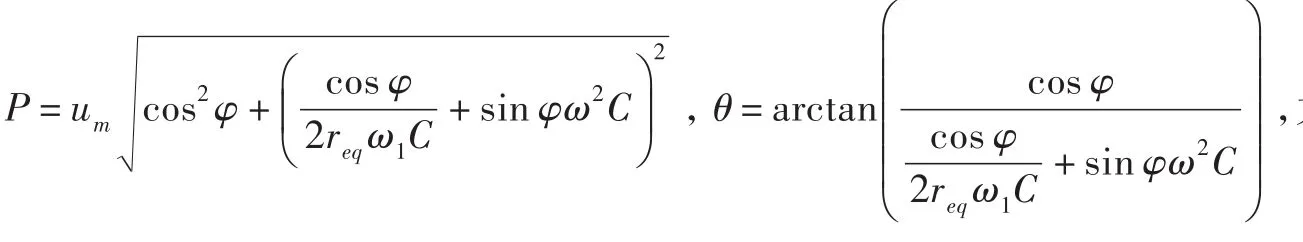
由式（17）可知，零序电压是一个以 ω1为振荡频率，以为衰减系数的衰减电压.

单相接地消失后，假设测得的零序电压周期为T，那么

因而，根据式（10）得到

因而可得对地电容C的表达式为

由此可测得系统对地电容的大小.

3 系统对地电容测量方案的实施

本文提出的电网对地电容和对地泄漏电阻的测量步骤可表述为：

（1）调节消弧线圈到任意档位（或匝数），此时的消弧线圈等效电感为L.

（2）选取电网任意一相，经该相到大地之间接一个较大的接地电阻（大到使得单相接地发生后继电保护装置不动作）.

（3）经过一定时间后，退出接地电阻，测量零序电压衰减过程中的周期T.

（4）将测得的周期T代入式（20）计算就可得到对地电容C的大小.

在采用本方法测量电力系统对地电容时，接地电阻的选取不宜过大或过小，接地电阻过大会造成测量精度较低，接地电阻过小会造成的单相接地事故，使得继电保护装置动作，影响供电可靠性.另外值得注意的是，该方法由于需要人为设置故障相，因而仅能用于线下测量.

4 仿真验证

在Matlab/Simulink中搭建如图4所示的仿真模型，参数设置为：6 kV系统，消弧线圈等效电感0.4 H，系统对地泄露电阻为4000 Ω ，接地电阻为5000 Ω ，预设对地电容为20、50、80和120 μF，泄露电阻4000 Ω ，仿真时间为1 s，在0 s时刻，单相接地消失（即图4中开关断开）.

零序电压的（对地电容依次为20 μF、50 μF、80 μF和120 μF）波形如图5所示.

为便于测量零序电压周期，选取0.2～0.3 s为观察时间段，零序电压波形如图6所示.

其中，

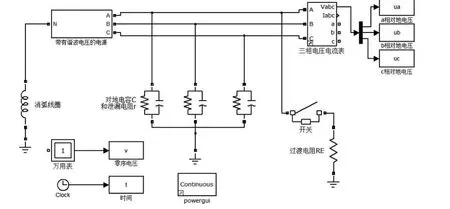
图4 Matlab/Simulink仿真模型

根据图6测得不同对地电容系统周期（单位s），以及根据式（20）计算所得到的电容值与实际电容值比较如表1所示.

由表1可知，该简化方法可以较为精确地测量系统对地电容.另外根据该方法的原理可知，该方法可以消除系统谐波电压分量的干扰，操作简便.

图5 不同对地电容系统零序电压的波形

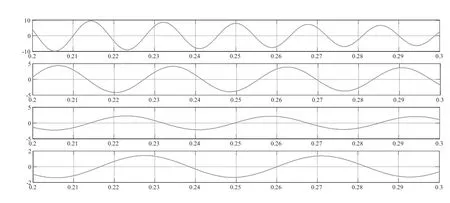
图6 0.2～0.3 s内零序电压波形

5 结论

本文提出了一种可实现配电网对地电容精确测量的方法，该方法利用了单相接地故障消失后零序电压振荡频率与系统对地电容的关系，实现了系统对地电容的精确测量.该方法可消除系统电源电压中谐波分量的干扰，操作简单，测量精度高.

[1]李毅敏，蔡旭.基于信号注入法的对地电容检测系统[J].电工技术，2007（3）：31-34.

[2]王崇林.中性点接地方式与消弧线圈[M].徐州：中国矿业大学出版社，1999：1-111.

[3]李晓波，王崇林，宗剑.单相经电阻接地测量6～10 kV电网电容电流可行性分析[J].电测与仪表，2008（3）：23-27.

[4]要焕年，曹梅月.电力系统谐振接地[M].北京：中国电力出版社，2001：81-82.

[5]李毅敏.基于信号注入法的对地电容检测系统[J].电工技术，2007（3）：31-34.

[6]易文韬，李甦康. 配电网电容电流测量方法探讨[J].江西电力，2010，34（1）：13-17.

[7]Hanninen S,Lehtonen M,Hakola T.Earth faults and related distribution networks[J].IEEE Proc-Gener Transm&Distrib,2002,149(3):283-288.

[8]Stefan WILL,Klaus SCHILLING.Reliability analysis of MV networks with different neutral earthing schemes[C].17th International Conference on Electricity Distribution,2003,12(15):12-15.