视频点播系统中视频分片协同存储方案研究

赵晓明，周颢，何军，赵保华

（1. 中国科学技术大学计算机科学与技术学院，230027，合肥；2. 安徽省计算与通讯软件重点实验室，230027，合肥）

随着无线网络的迅猛发展，无线网络提供的高速率传输使得视频点播系统(Video on Demand，VoD)业务呈现爆炸性增长。如何利用有限的资源将海量的视频数据存储起来成为研究热点[1-4]。

目前VoD视频存储研究的主流是利用服务器网络内部的高速链路来整合各个节点的存储能力从而能够胜任大规模的视频库存储，即协同存储。这需要考虑多方面的因素，例如服务器容量限制、链路带宽限制、视频内容流行程度分布等。本文将视频协同存储与网络编码[5]相结合，提出了一种视频分块协同存储最大本地命中算法，能够得到最优化的解决方案，并且当视频的总容量与服务器的总容量之比较大时，依然有较好的表现。

1 背景以及相关工作

1.1 研究背景

无线互联网正在蓬勃发展中，视频流量出现爆炸性增长。VoD系统由于摆脱了时间、空间的限制，具有方便、快捷的优点，因而具有广泛的应用。如图1所示是一种应用场景，利用长期演进（Long Term Evolution，LTE）网络中服务网关上的存储能力为用户提供视频缓存服务。

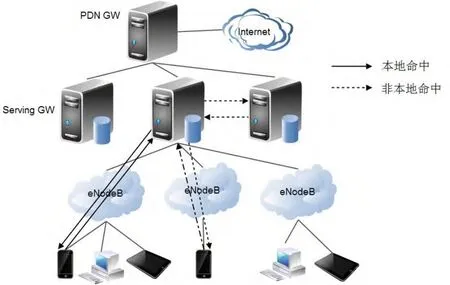
图1 VoD系统在长期演进LTE网络的应用场景

在LTE网络及其他VoD系统应用场景下，为有效存入海量视频库，引入了协同存储方案。每个服务器存储视频库的一个子集，并将其存储内容通过直接响应的方式为用户提供服务或者通过协作请求为其他的服务器提供服务。对于用户发出的视频请求，如果对应的服务器上有这个视频的备份，则称之为本地命中；否则，需要从其他的服务器上获取该视频，称之为非本地命中。因此，如何将这些视频分布式协同存储到服务器网络中有重要意义。

1.2 相关工作

在视频协同存储中，对不同的目标进行了研究。Applegate等基于硬盘空间、链路带宽、视频内容流行程度等约束条件以最小化总的数据量为目标进行研究[1];Borst 等将协作存储和路由联系起来，以最大化服务节点能够提供的流量并最小化总带宽的花费为目标进行了探讨[3]。然而，他们所提算法复杂度太高，应用场景也有局限。Xie等基于底层、非结构化的简单网络利用交通工程和协作存储从ISP的角度以最小化最大的拥塞程度为目标进行研究[2]。该算法需要判断请求的模式，这显然不实际。He等提出以最大化系统本地命中率为目标的快速近似最优的存储方法，以提高系统本地命中率为目标提出了一个快速贪婪算法[6]。

1.3 基于网络编码的视频协同存储算法

传统的通信网络传送数据的方式是存储转发，即中间节点不对数据内容做任何处理，只进行转发。网络编码[5](Network Coding, NC)通过中继节点对接收到的信息进行编码来达到提高多播网络容量。在网络中的各个节点上对各条信道上收到的信息进行线性或非线性的处理，然后转发给下游节点。

在VoD系统中，可以利用网络编码预先将视频进行分片编码。在接收到视频请求时，将编码后的视频片发给用户。客户端接收到足够的视频片后可进行解码，从而得到完整的视频。

采用NC编码能有效提高存储效率，提高系统可靠性。本文研究的目标是将前期的问题[7]与NC编码的分块存储相结合，提出基于NC编码的视频分块协同存储方案，使得本地命中率最大。

2 系统建模

建立一个VoD系统，视频集合为N，视频ni∈N原始的大小是si。采用NC编码，每个切片的大小为。由NC编码的原理可知，对于视频ni，系统中可以产生任意数目的切片。而在这些切片中，用户至少需要获得才能恢复出视频。

服务器集合M用来存储视频，服务器mt∈M的可用容量为Wt。在实际中，si＜＜Wt。假定视频ni在服务器mt上的访问频率为，视频ni在服务器mt上存放的视频切片块数为。定义变量如表1所示。

表1 各种变量的定义列表

在VoD协同存储中，本地命中越多，网络中流量就会变得越少，从而节省大量的带宽。因此，提出基于分片的最大命中问题(Maximum Hit Problem based on Segment，MHPS)的表达式为

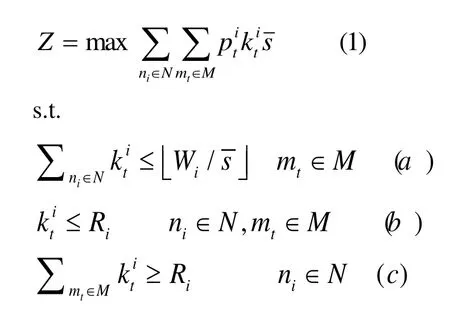
约束条件(a)表示对于服务器mt，所存储的视频的总容量不得大于mt的容量；约束条件(b)表示对于视频ni，在服务器mt上放置的片段数目不得大于Ri；约束条件(c)表示对于视频ni，系统中所存储切片总数必须能够保证恢复出该视频。

3 基于最小费用流问题的MHPS

最小费用流问题是指在给定网络中求从一个源节点到目的节点流值为某一常数的流，使其费用最小[7]。该问题有着广泛的应用，例如物流管理、供应链研究等领域。

本节构造出一个资源分配有向图GMHPS，证明了图GMHPS上最小费用流问题的解就是问题(1)的解，然后给出相应的算法。

3.1 资源分配有向图MHPSG

定义图GMHPS=(V,E)，其顶点集合为V=M∪N∪ {s,t} ∪ {sremain,vremain}，其中，sremain、vremain为虚拟节点，|V| =O(N+M)。

图GMHPS的边主要由7类组成，如表2所示。

表2 GMHPS 边的类型

假设边e的起始顶点为estart，终止顶点为eend，边e的容量函数为

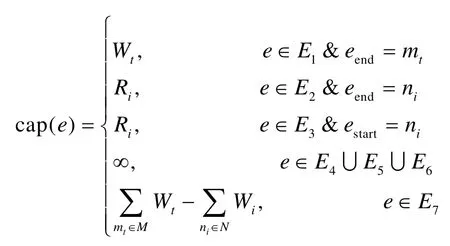
边e花费函数为

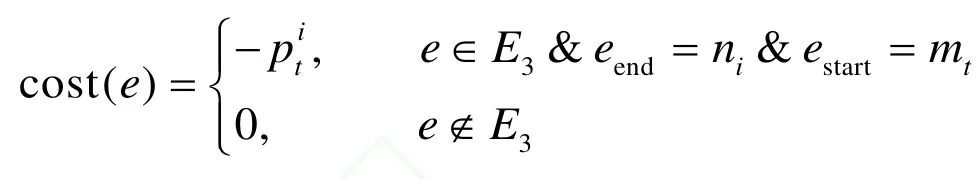
当 |M|=2，|N|=3时，GMHPS系统如图 2所示。

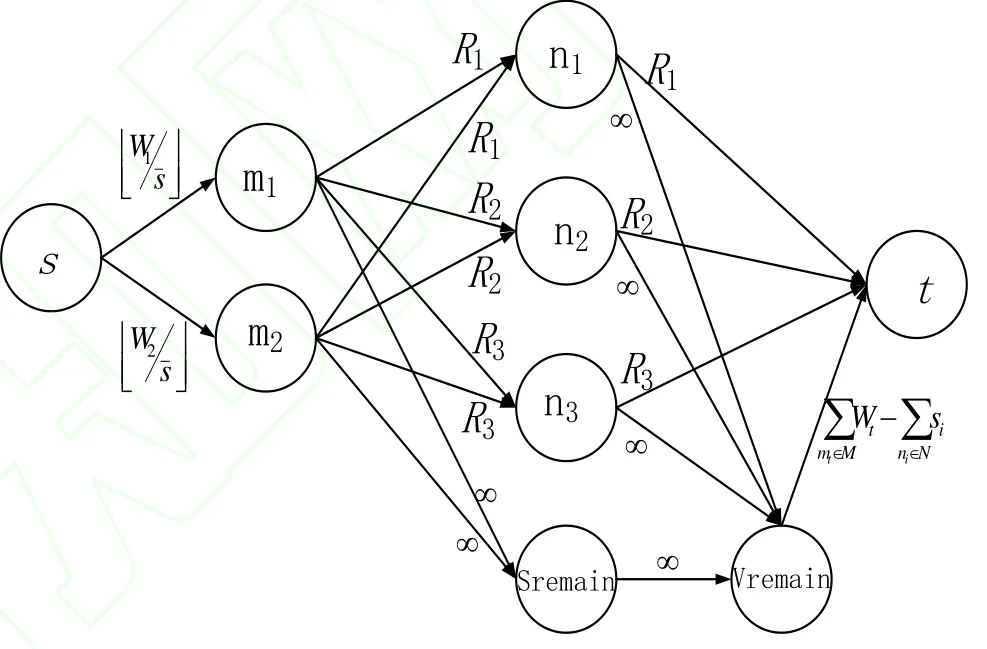
图2 | M |=2,| N |=3时 GMHPS 图

GMHPS中，从s节点流入的流量即为系统中服务器的总容量。s到mt边的容量为服务器mt所能存放的切片数，即。由于从s流入的流量为所有s到mt的边容量的和，所以每个s到mt边的流量也一定是mt能够存放的切片数目。

边mt到ni的容量是恢复ni所需要的最小切片数，而其上的流量则表示ni在mt上放置的片数。边ni到t的容量是恢复ni所需要的最小切片数，由于网络流的流量守恒特性以及vremain到t的容量可知，边ni到t的流量等于边的容量。

此时，视频ni在服务器mt上的存放片数kti即为从服务器mt到该视频ni的流量（GMHPS图中网络流的单位为切片的大小），从而求解出MHPS问题。例如，图 3表示GMHPS的一个实例，边上的数字表示分配的流量，其中，视频n1从服务器m1和服务器m2上分别得到流量为 4和 3，则对应的分配方案就是=4，=3，其他同理。

因此，若图GMHPS上可行解为ψ，边 ＜mt,ni＞的流量为MHPS中kti的值。由kti组成的解决方案为MHPS的解。

3.2 GMHPS最小费用流的解为MHPS问题的解

设ψ是GMHPS的一个解，ξ是MHPS的一个解。下面从两个方面来证明ψ与ξ一一对应。

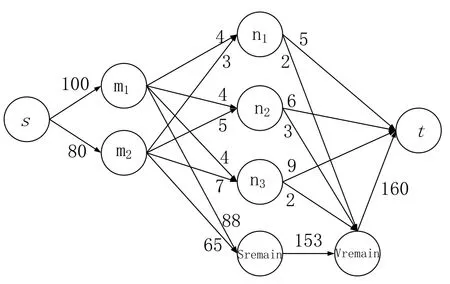
图3 图 GMHPS 与分配方案的关系

引理1GMHPS的解ψ是MHPS的解ξ。

假定ψ是GMHPS的一个解，根据GMHPS中E1集合的容量函数定义可知，服务器mt的流量最大为，满足约束条件（a）；同时，根据GMHPS中E2集合容量函数定义可知，视频ni放在服务器mt上的数目不超过Ri，满足约束条件（b）；由vremain到t的容量限制可知，每一个视频ni到t的流量至少为Ri，满足约束条件（c）。因此，ψ中服务器到视频集合的分配方案是MHPS的一个解ξ。

引理2MHPS的解ξ是GMHPS的解ψ。

假定ξ是MHPS的一个解，根据ξ中视频到服务器的分配方案，依照GMHPS的定义，可以构建出一个对应的图G的一个解ψ。因此，由ξ构造的解ψ是GMHPS的一个解。

综上，GMHPS的解与MHPS的解一一对应。因此，定理1显然得证。

定理1由GMHPS上最小费用流问题的解是MHPS问题的最优解。

3.3 算法及其时间复杂度

最小费用流问题已经有较多的实现[8-9]，Orlin等提出了多项式时间的原始网络单纯形算法[8]。在仿真实验中，利用LEMON[10]函数库进行求解。

GMHPS中 ，|V|=O(N+M)，|E|=O(NM)，GMHPS时间复杂度为O(NM)。LEMON库基于网络单纯形算法，其复杂度[8]是O(t2s2logt))，其中t和s分别是网路中节点数和边数。因此本算法时间复杂度是O((NM)2(N+M)2log(N+M))。在实际系统中，|N|＞＞|M|，所以本算法的时间复杂度为O(N4M2logN)。

4 实验仿真

4.1 仿真环境

在仿真试验中，建立一个VoD缓存系统，其中，单个服务器的容量大小从120 G到240 G随机分布。单个视频大小从20 M到400 M随机分布。

4.2 性能比较

这里将MHPS算法和两种算法进行了比较。第一种是文献[6]中提出的MHP算法，不考虑视频切片问题，直接将完整的视频存储于某个服务器。第二种算法是贪心算法MHPSG，即以访问频率的大小顺序来遍历视频库，将其存放到各个最优的服务器上，从而保证系统中存入了完整的视频库，运用多重背包问题将服务器剩余的空间尽可能多存储。

图4绘制了在服务器数目分别为10和20的情况下，当视频数目从100变到1 600时3种算法的性能。由图 4可见，①当服务器的数目和容量保持不变的时候，系统所获的收益呈现下降趋势，这是由于大量的低价值的视频分片占据了系统的容量，当视频片段数目达到一定的数目时，由于视频片段的总空间大于服务器的总空间，因而出现无解的情况；②对比不同的算法可以看出，MHPS算法优于MHP和 MHPSG算法。随着视频总容量的增加，MHPS算法的优势更加明显。例如当视频总容量达到服务器总容量的 90 %左右时，MHPS算法的性能超过MHP算法 10 %以上。

对于MHPS，显然，切片大小对系统的性能有影响。图5中绘制了在不同系统规模下，切片大小对系统性能的影响。

当切片数目过小时，由于大量收益低的视频切片会降低整个视频库视频切片的平均收益，从而导致系统性能下降。当切片数目过大时，容易造成系统空间浪费，导致系统性能下降。由图5可见，当切片大小为1 M，系统具有最佳的性能。因此，本文中选择了1 M作为默认的切片大小。

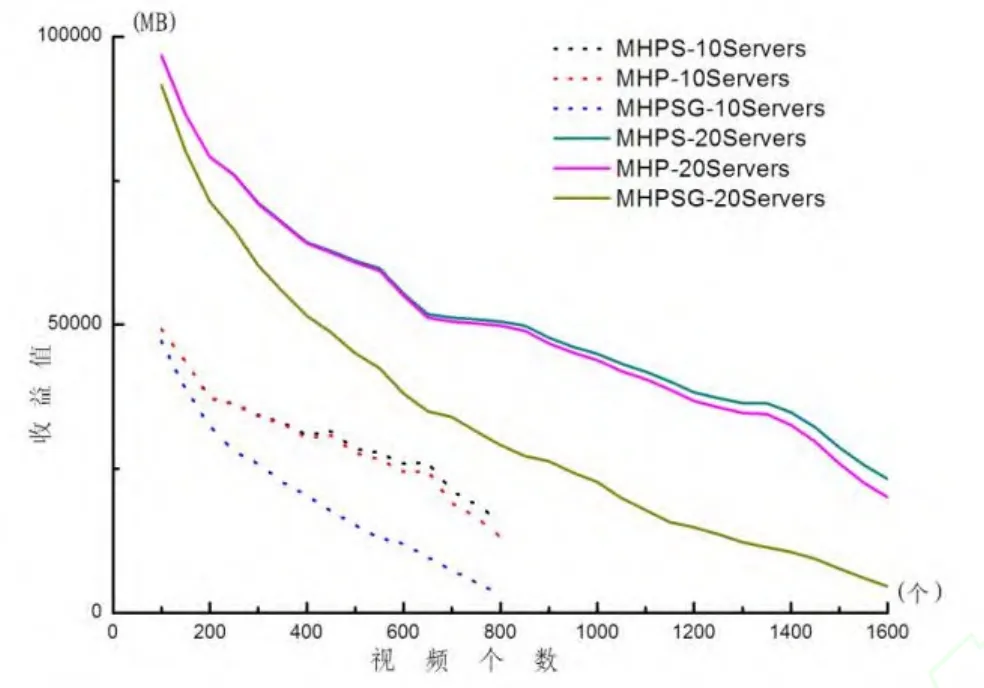
图4 不同算法获得收益的比较

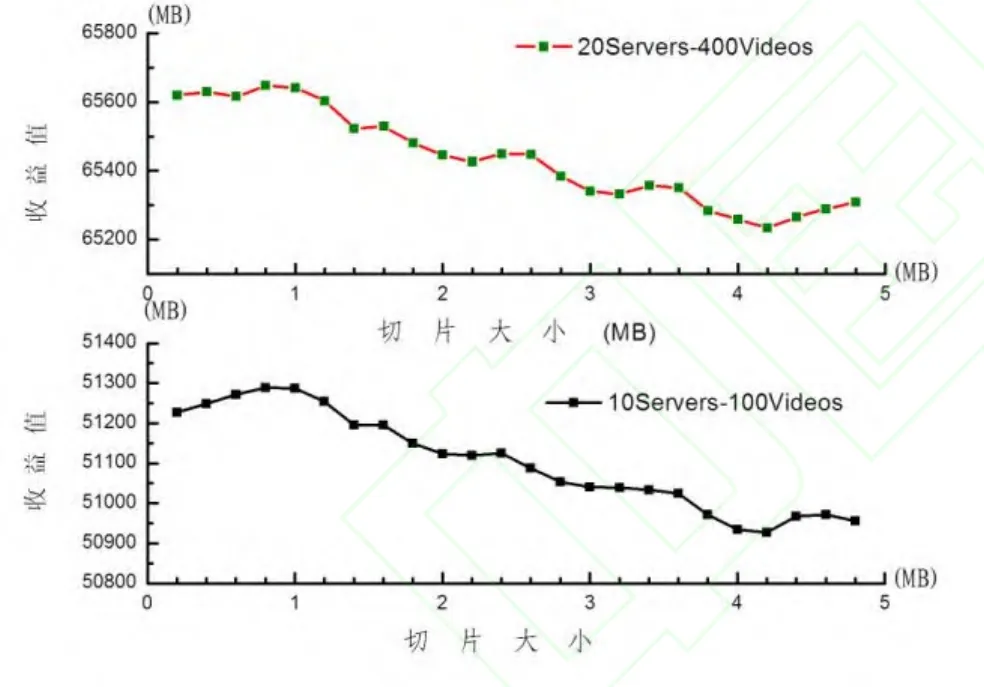
图5 不同系统规模下切片大小对系统性能的影响

5 结 论

VoD视频协同存储对于提高服务质量、提升用户体验、减小等待延迟等具有重要的意义，本文通过基于NC编码，对VoD视频协同存储问题进行了探究，提出了一个VoD系统中基于分片的视频协同存储解决方案 MHPS，该算法具有多项式时间复杂度。通过仿真，可以看出MHPS能够实现最优化的收益，该算法优于MHP算法，特别是在视频库的容量接近服务器的总容量的情况下，MHPS算法能够提供较大的收益提升。

[1]APPLEGATE D, ARCHER A, GOPALAKRISHNAN V, et al. Optimal content placement for a large-scale VoD system[C]// Proceedings of the 6th International Conference on Emerging Networking Experiments and Technologies.New York, USA:ACM, 2010：4.

[2]XIE Haiyong, SHI Guangyu, WANG Pengwei. TECC:towards collaborative in-network caching guided by traffic engineering[C]//Proceedings of the International Conference on Computer Communications. Piscataway, NJ,USA:IEEE, 2012:2546-2550.

[3]BORST S, GUPTA V, WALID A. Distributed caching algorithms for content distribution networks[C]//Proceedings of the International Conference on Computer Communications. Piscataway, NJ, USA:IEEE, 2010:1-9.

[4] ADAMIC L A. Zipf, power-laws, and pareto-a ranking tutorial [EB/OL]. (2000-04-10) [2013-11-16].http://impact.asu.edu/cse591sp11/ZipfParetoPowerranking.pdf.

[5]AHLSWEDE R, CAI Ning, LI S Y R, et al. Network information flow [J]. IEEE Transactions on Information Theory, 2000, 46(4):1204-1216.

[6]HE Jun, ZHAO Xiaoming, ZHAO Baohua. A fast, simple and near-optimal content placement scheme for a large-scale VoD system[C]// Proceedings of the 2012 IEEE International Conference on Communication Systems.Piscataway, NJ, USA:IEEE, 2012:378-382.

[7]AHUJA R K, MAGNANTI T L, ORLIN J B. Network flows:theory, algorithms, and applications [J]. Journal of the Operational Research Society, 1994, 45(11):1340-1340.

[8]ORLIN J B. A polynomial time primal network simplex algorithm for minimum cost flows [J]. Mathematical Programming, 1997, 78(2):109-129.

[9]DANTZIG G B. Linear programming and extensions[M].Berlin，Germany：Springer-Verlag, 1998:404-412.

[10]Egerváry research group on combinatorial optimization.Library for efficient modeling and optimization in networks [EB/OL]. (2011-06-07) [2013-11-16].http://lemon.cs.elte.hu.