基于CFD保亿中心风荷载三维稳态数值分析①
陈志强, 徐 伟
(同济大学土木工程学院,上海 200092)
0 引言
城市建设的高速发展,大量超高、复杂体型的建筑不断涌现,在杭州的钱江世纪城,超高层建筑更是密集,而作为控制高层建筑的重要荷载之一的风荷载,由于超高层建筑其表面风压分布极其复杂,体型系数超出现有规范[1]的适用范围.传统的风洞试验不能完全满足生产实际需要[2],而采用计算流体动力学(CFD)技术,当数学模型能比较准确反映问题本质时具有很大的优越性[3]:它不仅能够克服风洞试验的缺点,且提供信息全面.将CFD技术用于预测风荷载的作用以及风在建筑物周围的流场分布,找出结构的薄弱点,进行加强,具重要的现实意义.
保亿中心位于钱塘江畔的钱江世纪城,由主楼和底部裙房组成,主楼分A、B两座,A座总高度为106.3m,B 座总高度为178.05m,裙房 4 层,高 13.8m,采用钢框架-核心筒结构体系.因德国GMP将保亿中心设计成俯视图为“旋转风车”,建筑表面凹凸变化较多,A、B两座大楼间隔仅21米(如图1),具明显“狭缝效应”,因此为了保证结构设计的安全、经济、合理,对该大楼进行风荷载的CFD数值模拟计算,计算主要针对B座大楼,A座大楼作为干扰建筑.
1 CFD数值计算的原理
计算机技术和数值模拟方法的快速发展,采用CFD对钝体绕流进行数值分析,提取建筑物表面风压和周围流场的技术已经比较成熟[4~5].
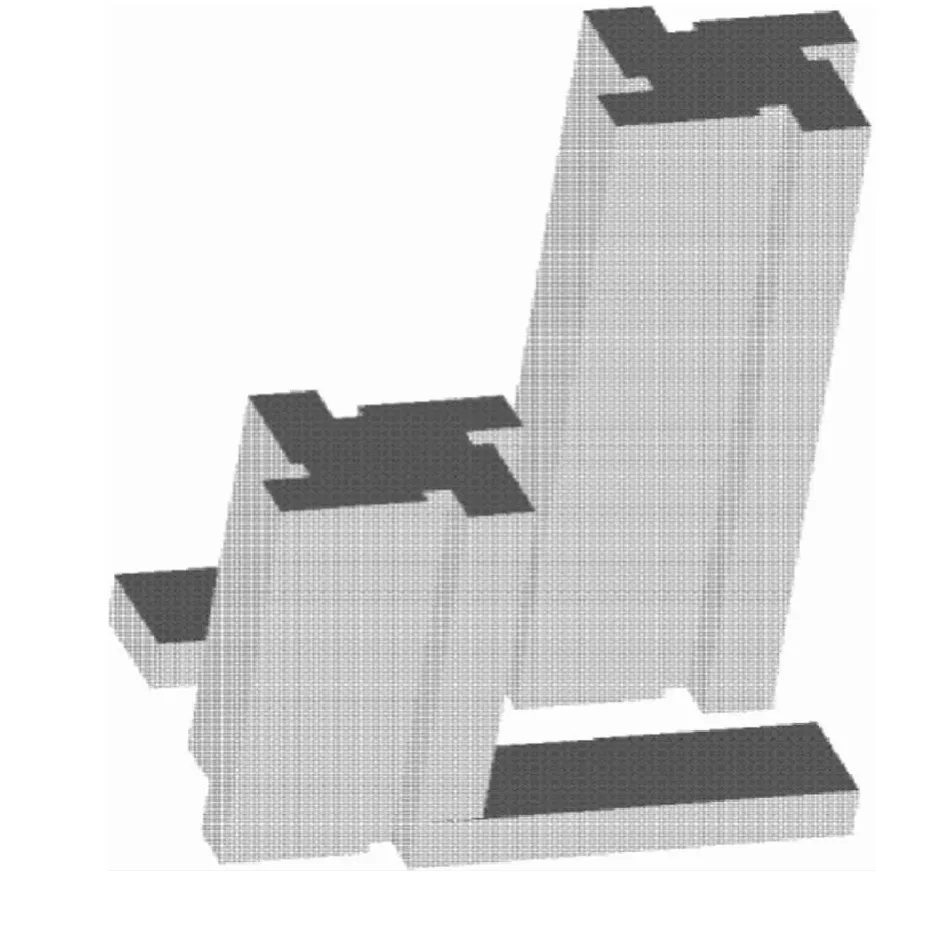
图1 保亿中心设计方案及CFD模型
本文采用可实现 k–ε湍流模型[6],可实现的k–ε湍流模型能更好的反映湍流的各项异性性质.在对建筑物进行数值模拟中,它比标准k–ε模型具更高的精度[7],可实现的 k–ε湍流模型其控制方程[8]如下:
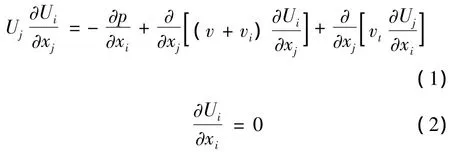

图2 三维整体网格划分
湍流动能k和湍流动能耗散率ε的控制方程如下:
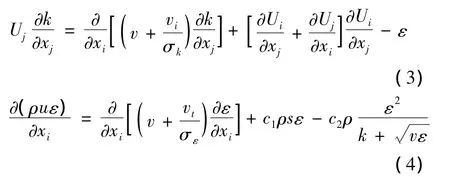
式中:Ui(i=1,2,3)为 x,y,z方向平均速度;P 是压力;v表示气流运动粘性系数表示涡团粘滞系数;ρ是空气密度.
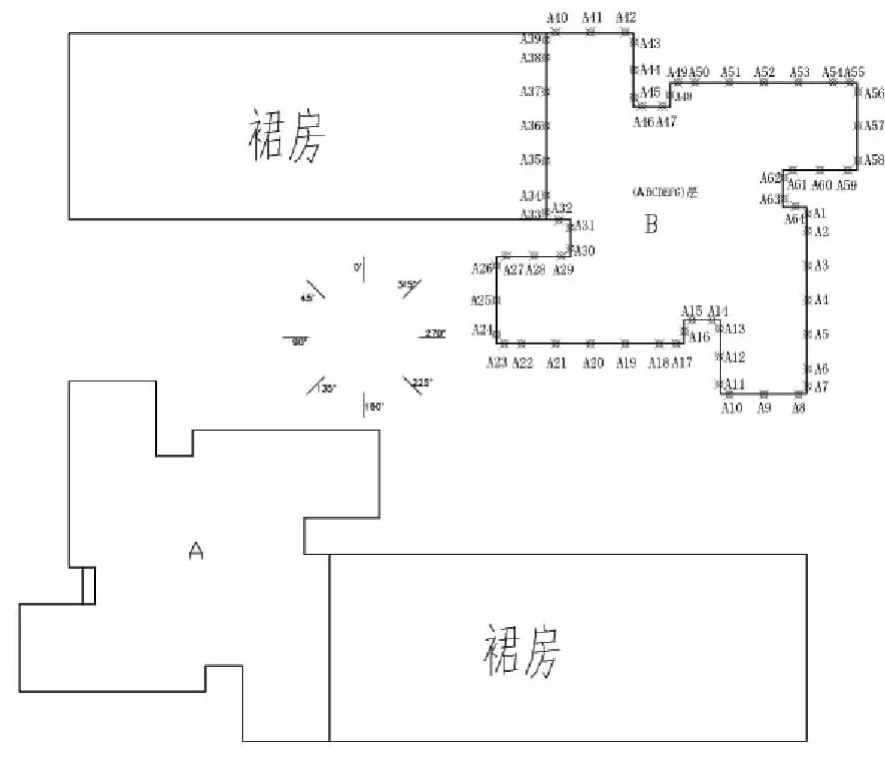
图3 B座主楼各层测点平面布置图
2 CFD数值建模和基本设置
2.1 网格划分
根据保亿中心建筑方案进行建模(如图1所示),整个计算流域范围确定为长度2600m(顺风向),宽度1200m(侧风向),高为720m的三维空间,该建模的空间区域足以涵盖保亿中心的影响范围.由于保亿中心结构体型很不规则,故对上述计算区域采用不同网格划分方式:建筑单体附近区域按非结构的四面体网格设置;建筑单体表面附近则选择加密网格;远离建筑单体的区域则设置成六面体结构网格形式,网格划分大小从内向外逐渐增大,共约生成1850000个网格.整体图2所示.
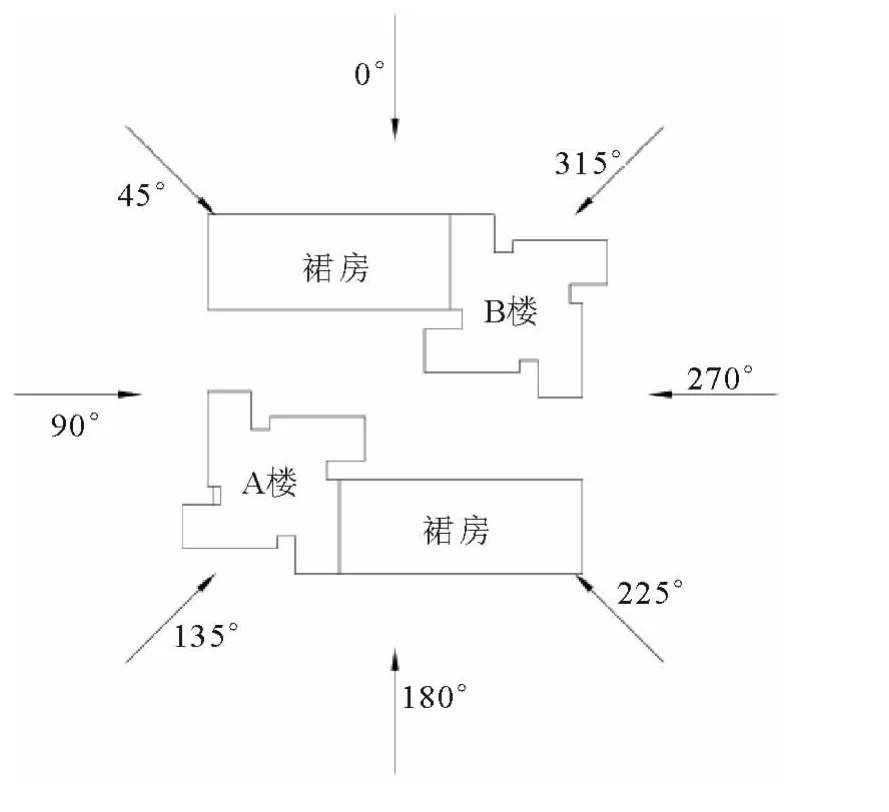
图4 CFD计算的风向角示意图

图5 135°风向角下的风压等值线图
2.2 速度入口
大气边界层模拟计算流域的进流面选择速度入口,入口处的湍流强度按照日本规范[9]建议的公式:式中:A是常数;H是参考高度;Z为离地面高度,指数α取0.16,离地高度30米(Z)处的湍流强度IU=16%.
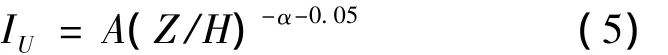
2.3 近壁面的处理
本文采用比标准的壁面函数法更具对压力梯度和偏移平衡点进行部分说明能力的非平衡的壁面函数法(Non-equilibrium Wall Functions)来处理近壁面的湍流状态.
2.4 计算工况及风向角
在建筑物表面布置测点,利用fluent软件提取各测点的风压系数,来计算风荷载.本次计算主要针对B楼主楼部分,为了计算B座大楼的风载合力和层体型系数,在B楼主楼上分7层布置测点,每层提取64个风压点,共提取了448个风压点的数据,风压数据点的各层测点平面布置见图3.
保亿中心建筑方案为非对称结构,在0°~360°风向范围内每隔45°选取一个风向角作为计算工况,各工况的风向角按逆时针设置如图4所示.
3 计算方法选择
采用FLUENT6.3软件,对流项的离散采用了一阶迎风格式,速度压力耦合采用SIMPLEC(SIMPLE- Consistent)算法,残差精度控制为0.001.
4 CFD数值计算结果与分析
(6)式中:μsi表示i点的风载体型系数,Cpi是建筑物表面某测点i的风压系数;μzr计算参考点的风压高度变化系数;μzi表示i点的风压高度变化系数.
根据各测点的坐标位置提取出不同测层处各测点的风压值.根据式(6)等,由各测点的风压值可计算出相应的风压系数及体型系数.
4.2 用于设计计算的主要承重结构风荷载参数
结合《建筑结构荷载规范》(GB50009-2012),通过计算风荷载合力,进而求出主楼沿x轴和y轴方向的层体型系数μs,供设计人员进行主体结构抗风设计参考.
4.2.1 风载合力计算
B楼主楼上的448个风压点的数据分布很不均匀,不能采用单一体型系数来描述楼层上复杂的三维风载,故将各个截面上受到的风压折算成作用于每米高度截面上的合力.扭转中心定义在B楼主楼的截面中心,扭矩以顺时针转为正.
通过计算,保亿中心B楼沿高度七个截面在各个风向角下风载合力 Fx,Fy和扭矩T,其中扭矩计算结果如表1所示.
通过计算可以获得8个风向角的风场,其中图5为135°风向角下的风压等值线图.
4.1 风载体型系数与风压系数
在不考虑阵风脉动和风振效应时,根据《建筑结构荷载规范》(GB50009-2012)规定,垂直作用于建筑物表面上某点的风压计算公式及CFD数值计算可获得各测点的风压系数,可得风载体型系数:

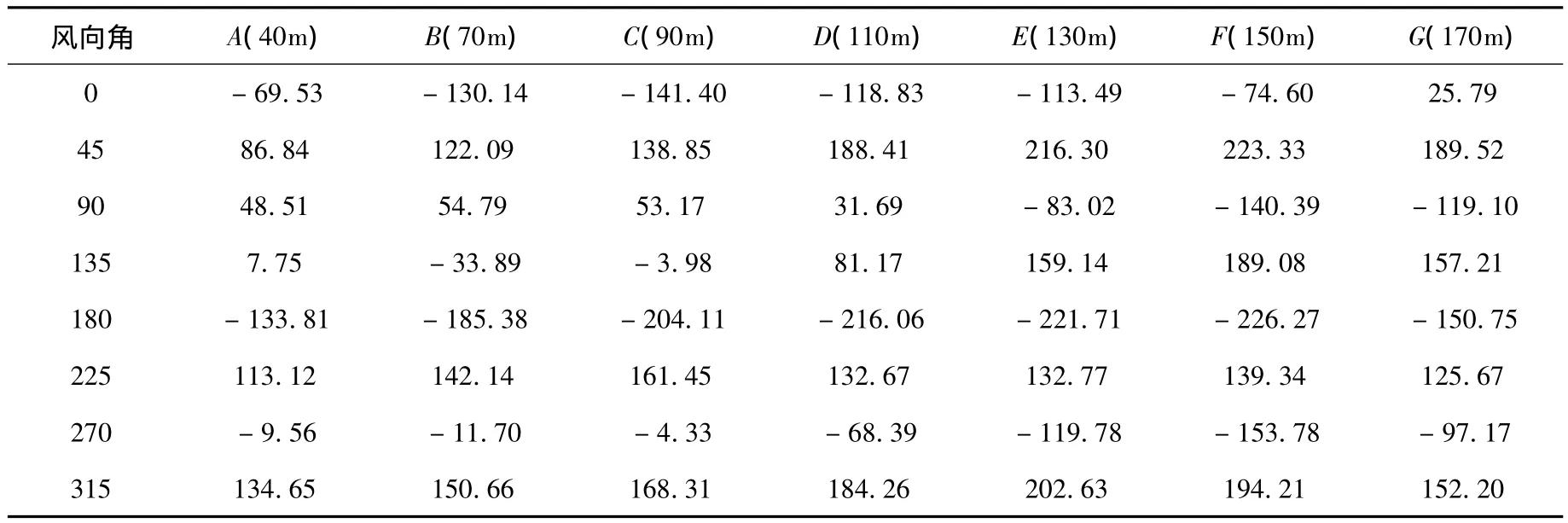
表1 所有风向角下各截面的扭转方向风载合力(T,单位:kN.m/m)
从表1中的扭转方向合力的相关数据可以看 出,大部分风向角下,B楼相对于中心的扭矩并不大.由于A楼的干扰作用,各层的扭矩大小有所不同.特别是90°和135°风向角下,A楼对B楼110m以下楼层的干扰作用十分明显.135°风向角下110m以下扭矩为负,这可能与该风向角下A楼对B楼产生明显的遮挡效应有关;而90°风向角下上下层的正负号变化可能与“狭缝效应”有关,靠近A楼一侧由于“狭缝效应”,风速会增大很多.总体而言,各层扭转效应从下到上逐步变大,顶层由于三维流效应略有减小.
4.2.2 层体型系数求解
定义平均层体型系数如下:
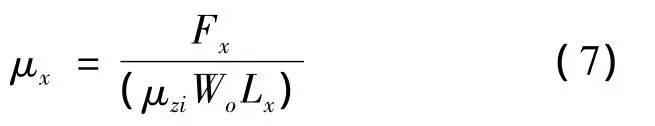
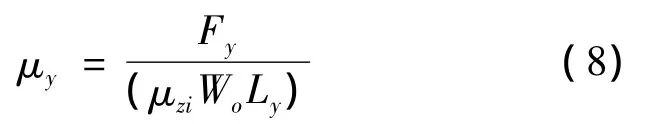
式中:μzi为该层对应的风压高度变化系数,Fz,Fy,Lx,Ly分别为风载合力和各层在 x轴和 y轴的特征长度.保亿中心B楼的Lx和Ly均取为52.3m.采用公式(7)、(8)以及各截面的风载合力可以计算出楼层的平均体型系数,用于承重结构的设计.楼层各截面在各个风向角下层体型系数,y方向如表2所示,同时在图6中图示给出了各截面y方向的层体型系数沿高度的分布.
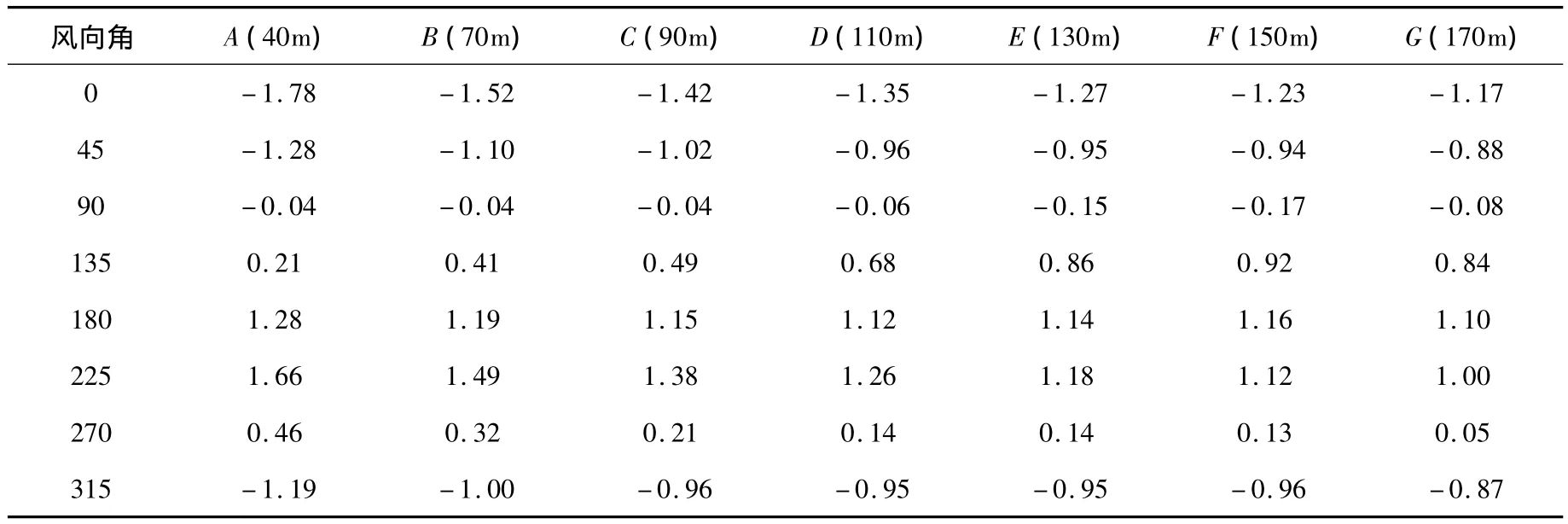
表2 所有风向角下各截面的层体型系数(y方向)
从上述图表及计算,对于保亿中心大楼,较大的层体型系数数据出现在以下风向角:45°和90°(x方向正值),270°(x方向负值);225°和180°(y方向正值),0°(y方向负值).
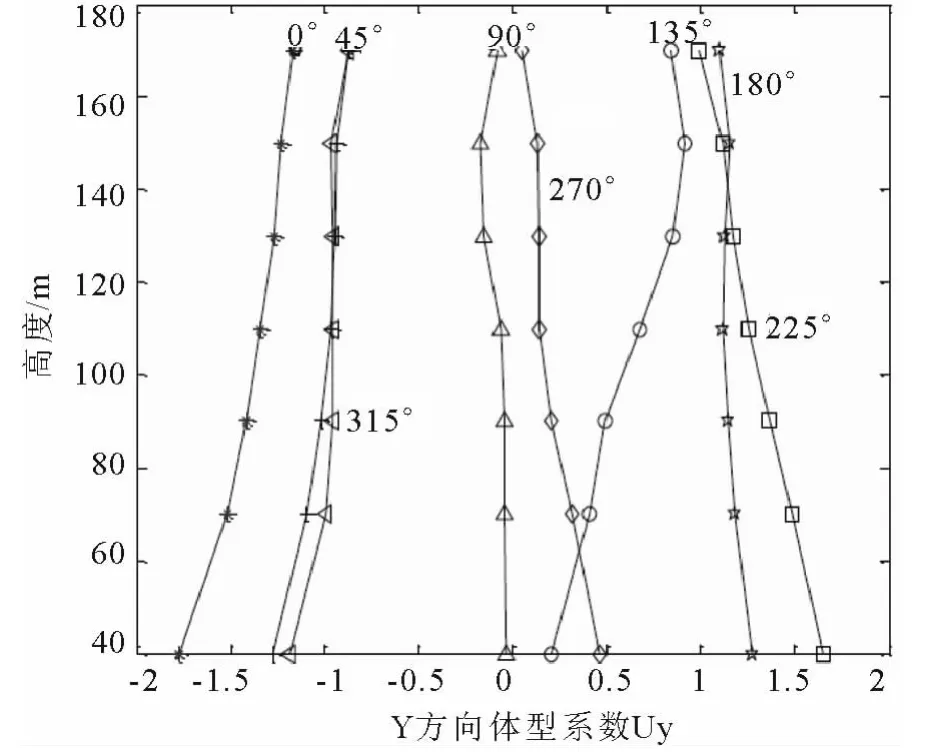
图6 各风向角下方向的层体型系数
5 结论
(1)本数值分析采用100年一遇的基本风压0.5kN/m2,如在设计中采用50年一遇的基本风压,则在使用本文的风压数据时须乘以0.9(=0.45/0.5)的转换系数,但在使用层体型系数的数据时不需要乘以该转换系数.
(2)地貌指数采用B类地貌,指数α =0.16,平均风速沿高度按指数规律变化,风场湍流度沿高度按指定公式变化,在离地面高度30m处要求湍流强度为I=16%,在CFD中风速剖面和流度分布通过UDF编程在边界条件得到了实现.
(3)通过提取B座大楼表面448个点的风压,计算在B座大楼截面上的风荷载合力,给出B座大楼沿x轴和y轴方向的层体型系数,该层体型系数可供主体承重结构设计参考.层体型系数计算中,采用了迎风宽度Lx=Ly=52.3m.
(4)在承重结构设计时,结构的风荷载标准值可通过计算及根据表1等给出单位高度上的风载合力或表2(图6)等给出的层体型系数确定.较大数据出现在以下风向角:45°和90°(x方向正值),270°(x方向负值);225°和 180°(y 方向正值),0°(y方向负值).数值模拟结果表明保亿中心在各种工况下,最大正负压区出现在转角处,尤其是大楼高度为40米左右楼层转角区域,其次是70米附近拐角处.对于建筑物外墙面的玻璃幕墙等外装饰外墙设计应特别注意负压较大区域,同时注意各风向角下的扭矩,但对于该主楼扭矩不大.
[1]中华人民共和国国家标准:建筑结构荷载规范(GB50009-2012)[S].北京:中国计划出版社,2012,33.
[2]CHEN Qing- yan,SREBRIC J L.Application of CFD Tools for Indoor and Outdoor Environment Design[J].International Journal on Architectural Science,2000,1(l):14-29.
[3]SPALDING D B.Mathematics and Computers in Simulation[M].Holland:North Holland,1981,23:267-276.
[4]黄本才,汪丛军.结构抗风分析原理及应用[M].第2版.上海:同济大学出版社,2008,134.
[5]卢旦.风致内压特性及其对建筑物作用的研究[D].杭州:浙江大学,2006,103.
[6]Shih T H,Liou W W,Shabbir A,Yang Z,Zhu J.A new k-ε Eddy-Viscosity Model for High Reynolds Number Turbulent Flows- Model Development And Validation[J].Computers Fluids,1995,24(3):227-238.
[7]杨伟,顾明.高层建筑三维定常风数场数值模拟[J].同济大学学报,2003,31(6):649―651.
[8]陶文铨.数值传热学[M].第2版.西安:西安交通大学出版社,2001,350-351.
[9]Architectural Institute of Japan.Recommendations for Loads on Buildings(2004)[S].Tokyo:Architectural Institute of Japan,2004,6-14.

