二级倒立摆最优控制实验①
栾 迪
(南京理工大学紫金学院,江苏南京 210046)
0 引言
二级倒立摆是对准确性和快速性要求很高的非线性不稳定系统.它能有效地反映诸如可镇定性、鲁棒性、随动性以及跟踪等许多控制中的关键问题,是检验各种控制理论的理想模型[1~2].最优控制是控制理论中非常热门的控制方法,用它来设计二级倒立摆的控制方法,无疑成为研究的热点.
二级倒立摆系统的结构如图1所示,机械部分主要有小车、下摆、上摆、导轨、皮带轮、传动皮带等,控制对象由小车、下摆、上摆组成,电气部分由电机、晶体管直流功率放大器、传感器以及保护电路组成[3].
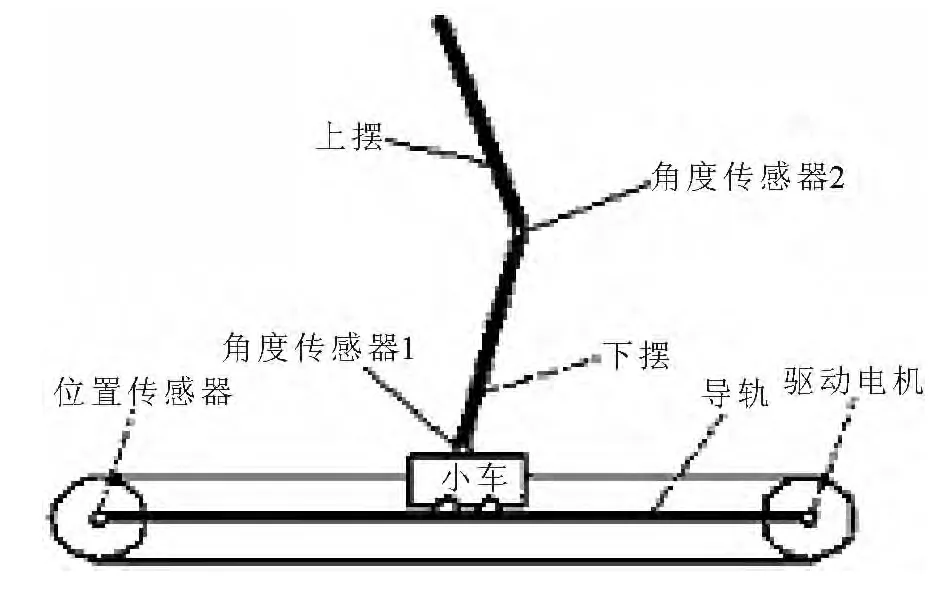
图1 二级倒立摆物理模型示意图
假设条件:
(1)上摆、下摆及小车都是刚体;
(2)皮带轮与皮带之间无相对滑动,传动皮带无伸长现象;
(3)小车的驱动力与直流放大器的输入成正比,忽略电机绕组中的电感;
(4)小车运动时所受的摩擦力正比于小车的速度;
(5)下摆转动时所受的摩擦力矩正比于下摆的转动速度;
(6)上摆运动时所受的摩擦力矩正比于上摆对下摆的相对角速度.
1 线性二次状态控制器(LQR)设计
1.1 线性控制器(反馈阵K)
设状态反馈调节率的形式为 u*(t)=-Kx(t),通过使性能指标函数即式(1)为最小,可求得状态反馈增益阵K.最优性能指标满足如式(2)的黎卡提方程[4~5].最优性能指标如式(3)所示.
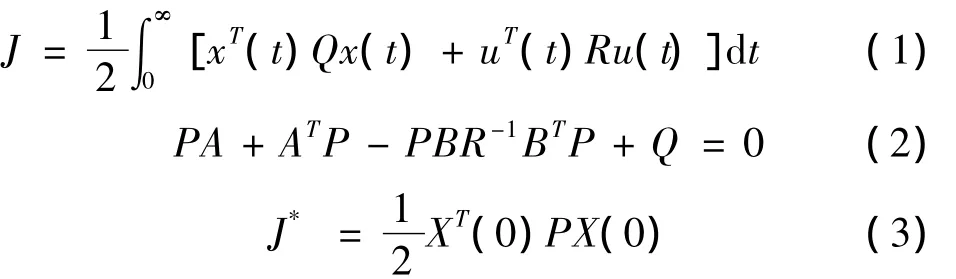
在matlab中用以下语句可得状态反馈增益阵K和满足式(2)黎卡提方程的唯一对称正定解P.
Q=2*eye(6),R=1.6,
P=are(A,BB,Q),K=inv(R)*B'*P
可以得到结果:
k=[0.8839-91.2426 86.1288 1.0498-6.2024 11.3657 ]
综上所述,PVT1在肝癌中明显高表达,其表达水平与肝癌患者TACE术后缓解程度、复发和生存率密切相关,可作为预测肝癌患者TACE预后的潜在分子标志物。
计算最小性能指标:
x0=[0,15*pi/180,10*pi/180,0,0,0]';%初始条件,J=0.5* x0*P* x0'
得到 J=4.4146.
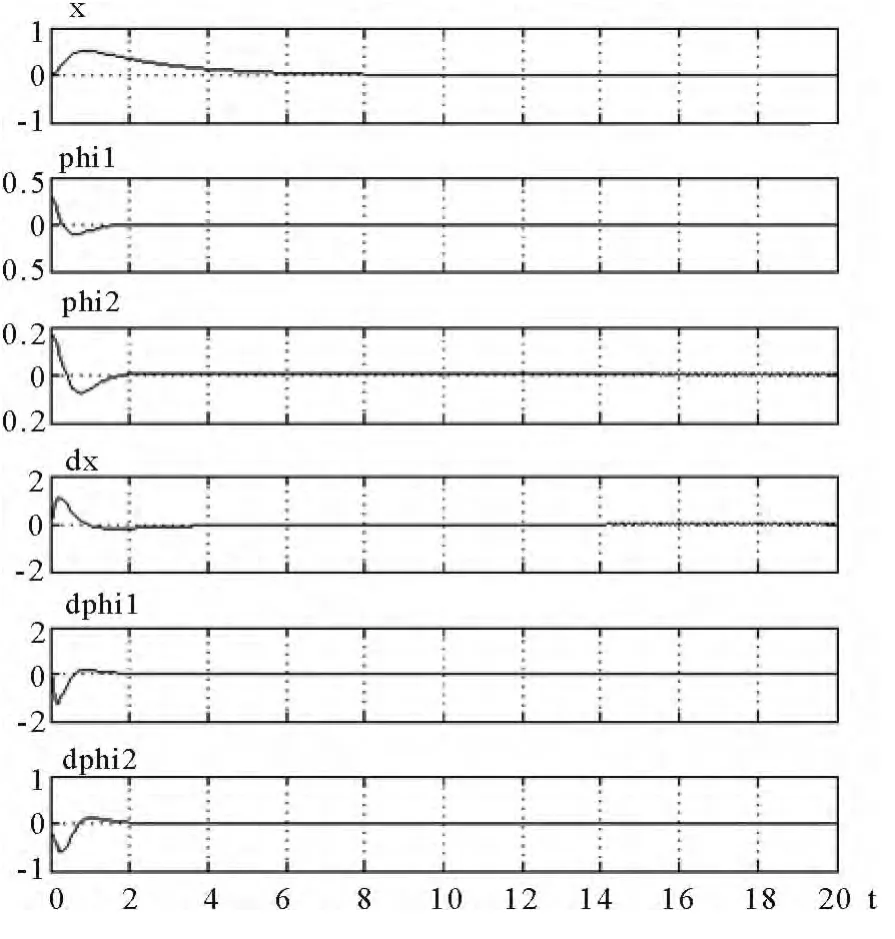
图2 LQR法各状态变量响应曲线
1.2 仿真结果
从仿真曲线图2可见,系统稳定,达到要求.
2 线性二次输出控制器(LQY)设计
2.1 线性控制器(反馈阵K)
设状态反馈调节率的形式为 u*(t)=-Kx(t),通过使性能指标函数(式(4))为最小,可求得状态反馈增益阵K.最优性能指标满足如式(5)的黎卡提方程.最优性能指标如式(6)所示.
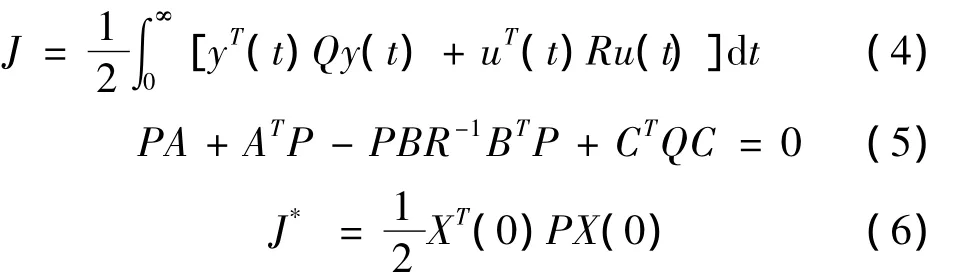
在matlab中用以下语句可得状态反馈增益阵K和满足式5黎卡提方程的唯一对称正定解P.

计算最小性能指标:
x0=[0,15*pi/180,10*pi/180,0,0,0]';%初始条件,J=0.5* x0*P* x0'
得到 J=3.8694.
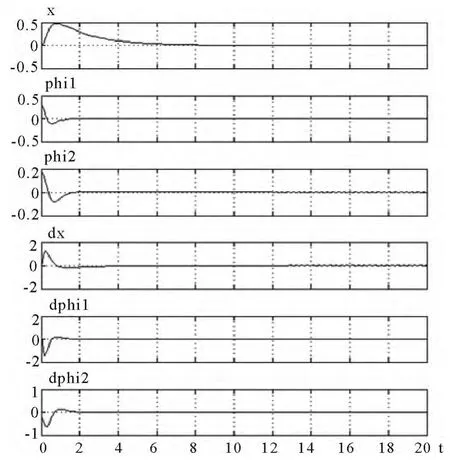
图3 LQY法各状态变量响应曲线
2.2 仿真结果
从仿真曲线图3可见,系统稳定,满足要求.
3 LQR与LQY法比较
为比较LQR法与LQY法的控制性能,对两种方法进行对比,仿真曲线如图4所示.
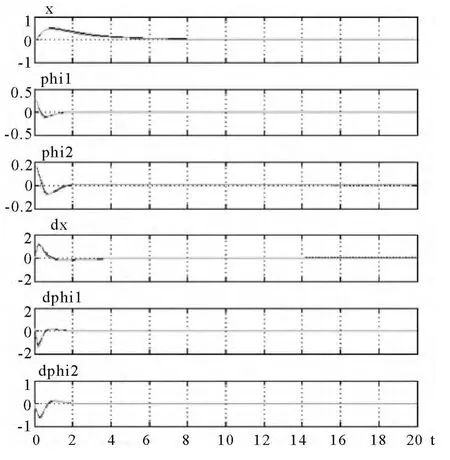
图4 LQR与LQY法各状态变量响应曲线对比
从仿真曲线图4中LQR算法和LQY算法的对比来看,LQR算法比LQY算法响应曲线好一点,但不是很明显.
可是从前面的计算结果看,有:
J*(LQR)>J*(LQY)
理论上应当J*(LQR)<J*(LQY),之所以出现这种情况,可能是LQR法在选择Q阵与R阵时没有使之达到性能最优.
4 结语
本文给出了二级倒立摆的最优控制方法,线性二次状态控制器(LQR)和线性二次输出控制器(LQY),并且给出了仿真结果.通过仿真可知,两种控制器都能够使得二级倒立摆系统稳定,达到预期的效果.且两种控制方法效果相当.
[1]张葛祥,李众立,毕效辉.倒立摆与自动控制技术研究[J].西南工学院学报,2001,16(3):12-16.
[2]宋君烈,肖军,徐心和.倒立摆系统的 Lagrange方程建模与模糊控制[J].东北大学学报(自然科学版),2002,23(4):333-337.
[3]郑科,徐建明,俞立.基于TS模型的倒立摆最优性能模糊控制[J].控制理论与应用,2004,21(5):703-708.
[4]Farwig M,Zu H,Unbehauen H.Discrete Computer Control of a Triple‐ Inverted Pendulum[J].Optimal Control Applications and Methods,1990,11(2):157-171.
[5]徐雄.倒立摆系统的研发及基于 MATLAB的实时模糊控制[J].电子测试,2007,5:2-5.

