位移谱阻尼调整系数的影响分析

王国弢胡克旭

（同济大学结构工程与防灾研究所，上海200092）

位移谱阻尼调整系数的影响分析

王国弢*胡克旭

（同济大学结构工程与防灾研究所，上海200092）

将848条地面加速度记录分别按矩震级（M）、观测点到断层面最近距离（Rrup）和场地条件进行分类，研究了M、Rrup、场地条件和重要持时（D5-95）对位移谱阻尼调整系数（DSFd）的影响。结果表明：M对DSFd的影响显著，Rrup对DSFd的影响较弱，场地条件对DSFd的影响微弱。D5-95是影响DSFd的一个重要因素。M、Rrup、场地条件和D5-95对DSFd的影响与阻尼比（ξ）和周期（T）有关：当ξ＞5%时，在T≥1 s的范围内，随着M、Rrup和D5-95的增大，DSFd减小，且ξ和T越大，DSFd减小的程度越大。当ξ＜5%时，在T≥0.2 s范围内，随着M、Rrup和D5-95的增大，DSFd增大且ξ越小，DSFd增大的程度越大。在短周期范围内（如ξ＞5%时，T＜1 s；ξ＜5%时，T＜0.2 s），M、Rrup和D5-95对DSFd的影响并不显著甚至有相反的趋势。在回归模型中，综合考虑M和Rrup两个参数可较全面地反映D5-95对DSFd的影响。

矩震级，观测点到断层面最近距离，场地条件，重要持时，位移谱阻尼调整

1 引 言

在结构的抗震设计中需要不同阻尼比下的弹性反应谱。目前，抗震规范普遍采用的方法是通过阻尼调整系数（DSF）从5%阻尼比的弹性反应谱去估计不同于5%阻尼比的弹性反应谱。现行抗震规范［1，2］中阻尼调整系数通常取决于结构的等效粘滞阻尼，在某些情况下，也与结构的等效周期有关。许多学者对阻尼调整系数进行了的研究，其中的一些成果已被EC8［1］、ATC-40［3］、FEMA273／356［4，5］和NEHRP［2，6］等采用。近年来，考虑震级、场地和距离影响，国内外学者对阻尼修正系数进行了更为深入的研究，Bommer and Mendis［7］认识到了持时对位移谱阻尼调整系数（DSFd）的影响，对阻尼比ξ＞5%的情况，提出了DSFd随矩震级（M）和断层距（R）的增大而减小的结论。Cameron and Green［8］认为DSFd与地震动的频谱特性和持时有关。Stafford等［9］在DSFd的回归模型中直接考虑了持时这个变量。Lin［10］研究了场地条件对DSFd和绝对加速度谱阻尼调整系数（DSFa）的影响。

本文基于所选的848条地震波对线弹性单自由度体系进行时程分析得出每条地震波的弹性反应谱数据，然后对这些数据进行统计分析进一步研究了矩震级（M）、观测点到断层破裂面的最短距离（Rrup）、场地条件和重要持时（D5-95）对位移谱阻尼调整系数（DSFd）的影响。

2 阻尼调整系数

阻尼调整系数可分为相对位移谱阻尼调整系数（DSFd）、相对速度谱阻尼调整系数（DSFv）和绝对加速度谱阻尼调整系数（DSFa）。它们分别被定义为

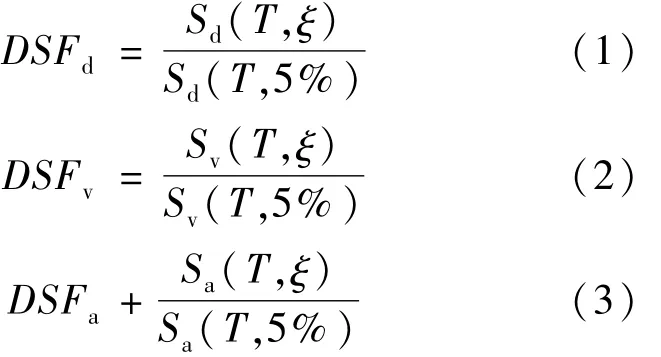
式中，Sd（T，ξ），Sd（T，ξ）和Sd（T，ξ）分别是相应于周期（T）和阻尼比（ξ）的弹性相对位移、相对速度和绝对加速度反应谱；Sd（T，5%），Sd（T，5%）和Sd（T，5%）分别是相应于周期T和阻尼比5%的弹性相对位移、相对速度和绝对加速度反应谱。

本文采用软件SeismoSignal对每条输入地震波进行计算，线弹性单自由度体系的自振周期取0.02～10 s，周期增量为0.02 s，阻尼比分别取0.5%、1%、2%、3%、5%、10%、15%、20%、25%和30%，计算方法采用Newmark逐步积分法，β＝0.251，γ＝0.5，从而可得出该输入地震波各个阻尼比的位移反应谱。将上述计算得到的不同阻尼比的位移反应谱除以5%阻尼比的位移反应谱就得到该条地震波不同阻尼比的位移谱阻尼调整系数。

3 地面运动加速度时程记录

在本文的研究中使用了848条地震加速度时程，这些地震加速度时程下载于太平洋地震工程研究中心的强震数据库（http：／／peer.berkeley.edu／peer＿ground＿motion＿database）。其中有802条地震加速度时程是在1975－2002年之间在美国西部所发生的地震过程中所记录到的；46条地震加速度时程来自于1999年台湾的集集地震。地震的最小矩震级为5，最大矩震级为7.62，观测点到断层破裂面的最短距离为0～100 km。本文将848条地震记录分别按矩震级M、观测点到断层破裂面的最短距离Rrup和地表厚度30 m内平均剪切波速Vs，30进行分组，分组情况见表1。其中，Vs，30≥360 m／s代表NERHP［2］中的A（Vs，30＞1 500 m／s）、B（760 m／s＜Vs，30≤1 500 m／s）和C（360 m／s＜Vs，30≤760 m／s）三类场地，可归类为岩石类场地；Vs，30＜360 m／s代表NERHP中的D（180 m／s＜Vs，30≤360 m／s）和E（Vs，30≤180 m／s）类场地，可归类为土质类场地。

表1 地面运动记录分组Table 1 Ground motion records

4 统计分析的结果

通过统计分析，可获得每组加速度时程记录（表1）位移谱阻尼调整系数的中值，然后按照各自的分组对其进行对比。在以下的四个小节中，分别研究了M、Rrup、场地条件和D5－95对DSFd的影响。

4.1 M对DSFd的影响

图1表明了在不同M的分组下，DSFd中值随周期T的变化。

如图1（a）和图1（b）所示，当ξ＜5%时，DSFd随M的增加而增加，这种趋势在T＞1 s范围内随周期的增长越加明显；当ξ＞5%时，在T＞1 s范围内，DSFd随M的增加而减少且这种趋势随周期的增长越加明显，在T＜1 s的范围内，M对DSFd无明显影响。M对DSFd的影响程度还与ξ有关，当ξ＜5%时，ξ越小，M对DSFd的影响越显著；当ξ＞5%时，ξ越大，在T＞1 s范围内，M对DSFd的影响越显著；DSFd受M影响的周期范围也与ξ有关，ξ＜5%受影响的范围比ξ＞5%时的要大。

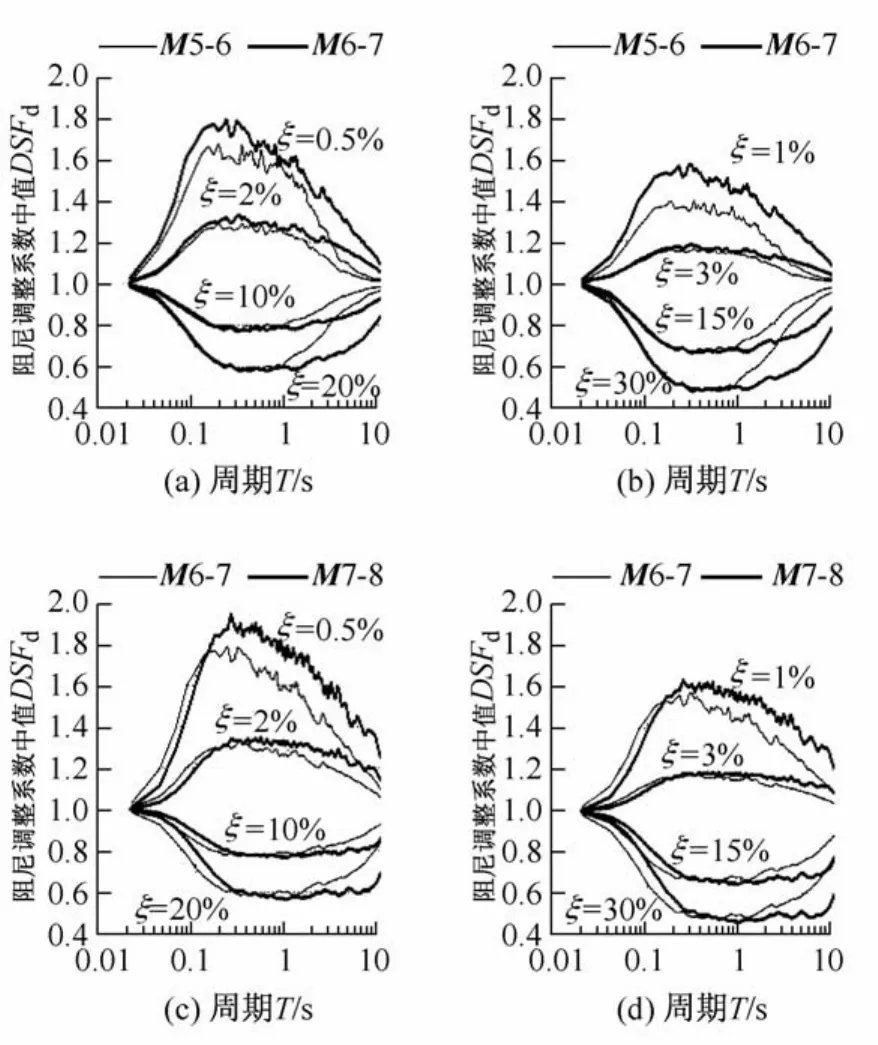
图1 M对DSFd的影响Fig.1 Influence of M on DSFd

从图1（c）和图1（d）中可以观察到与图1（a）和图1（b）类似的现象，但在ξ＜5%，大约在T＞0.2 s范围内DSFd随M的增加而增加。在T＜0.2 s，M对DSFd无明显影响或DSFd表现出与上述现象相反的趋势。从图1中均可见，在长周期处，随着M的增加DSFd偏离于单位1。

4.2 Rrup对DSFd的影响

图2表明了在不同的Rrup范围内，DSFd中值随周期T的变化。

如图2（a）和图2（b）所示，当ξ＞5%和ξ＝2%，3%时，Rrup对DSFd基本无影响；当ξ＝0.5%时，在短周期范围内，Rrup对DSFd有一定的影响，随着周期的增长影响消失。由此可知，近场地震动对DSFd基本上无影响。

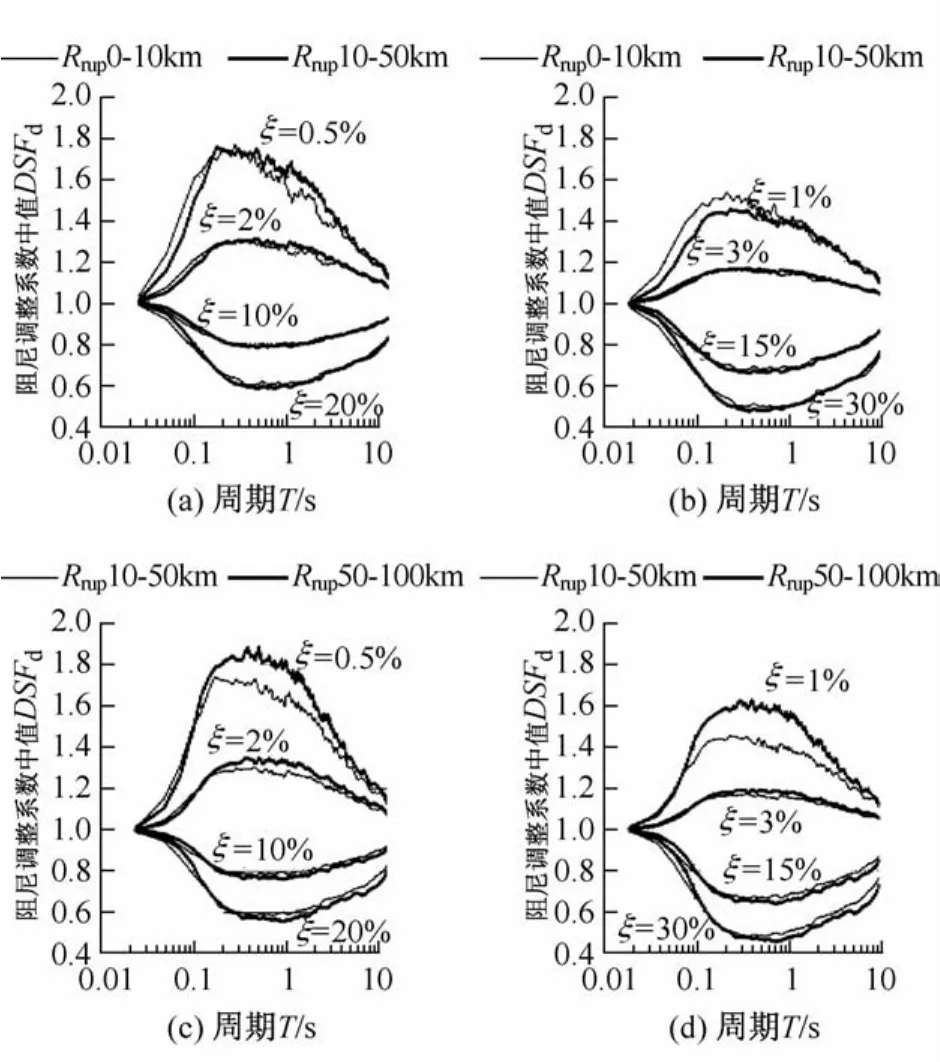
图2 Rrup对DSFd的影响Fig.2 Influence of Rrupon DSFd

如图2（c）和图2（d）所示：当ξ＜5%时，在T＞0.1 s的范围内，随Rrup的增大DSFd增大，ξ越小，DSFd增大的程度越大；当ξ＞5%时，在T＞0.1 s的范围内，随Rrup的增大DSFd减小，ξ越大，DSFd减小的程度有相应增加。在T＜0.1 s，Rrup对DSFd无明显影响或DSFd表现出与上述现象相反的趋势。与M对DSFd的影响相比，Rrup对DSFd的影响较弱。

4.3 场地条件对DSFd的影响

图3表明了在不同的场地条件分组下（Vs，30＞360 m／s和Vs，30≤360m／s），DSFd中值随周期T的变化。

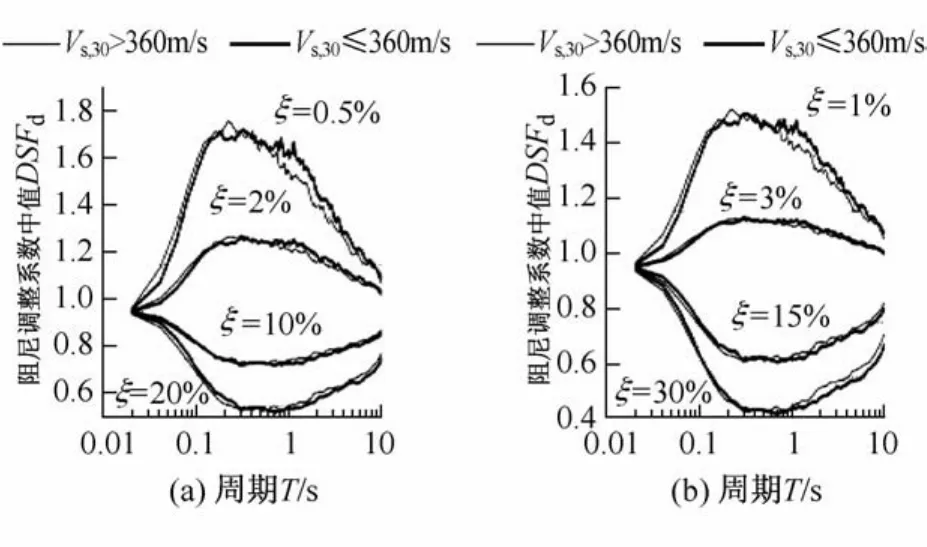
图3 场地条件对DSFd的影响Fig.3 Influence of site conditions on DSFd

如图3（a）和图3（b）所示，场地条件对DSFd的影响很微弱，仅在ξ较小和ξ较大时有一定的影响。其趋势为：当ξ＝0.5%，1%时，在T＞0.3 s范围内，随着Vs，30的增加（如Vs，30≤360 m／s增加到Vs，30＞360 m／s），DSFd有少量的减少；在T＜0.3 s范围内，随着Vs，30的增加，DSFd有微量的增加。当ξ＝30%在T＞0.3 s范围内，随着Vs，30的增加，DSFd有少量的增加；在T＜0.3 s范围内，随着Vs，30的增加，DSFd基本无变化。

4.4 D5-95对DSFd的影响

图4表明了T＝0.2 s，1 s和5 s时，DSFd与 D5-95之间的统计关系；为了直观，还在图中作出了DSFd和D5-95的线性拟合线。

如图4（b）所示，当ξ＜5%时，DSFd随D5-95的增加而增加且ξ越小这种趋势越明显；当ξ＞5%时，DSFd随D5-95的增加而减小且ξ越大这种趋势越明显。对比图4（c）和图4（b）可知，上述现象在更长的周期处更明显。在短周期处（如T＝0.2 s），如图4（a）所示，当ξ＜5%时，DSFd随D5-95的增加而增加且ξ越小这种趋势越明显；当ξ＞5%时，D5-95对DSFd基本无影响。对比图4（a）和图4（b）可知，D5-95对DSFd的影响在更长的周期处更明显。

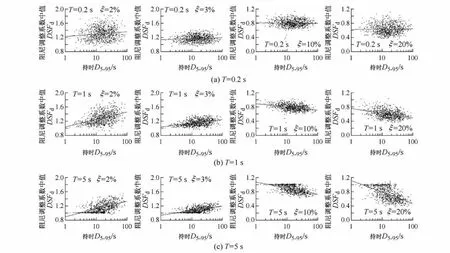
图4 D5-95对DSFd的影响Fig.4 Influence of D5-95on DSFd

综上，D5-95对DSFd的影响可描述为：

（1）当ξ＜5%时，DSFd随D5-95的增加而增加；当ξ＞5%时，DSFd随D5-95的增加而减小。

（2）在（1）中所述的DSFd随D5-95的变化趋势，当ξ＜5%时，ξ越小，越明显；当ξ＞5%时，ξ越大，越明显.

（3）在（1）中所述的DSFd随D5-95的变化趋势随周期T的增长越明显，随周期T的减小而变弱甚至有相反的趋势。D5-95对DSFd有影响的周期范围与ξ有关，ξ＜5%时，影响范围较ξ＞5%时的大，如图4（a）所示。

5 M和Rrup对DSFd的综合影响

由于各国抗震规范中并没有包含持时这个参数，所以在回归模型中直接包含这个参数，从实际运用的角度来说是不理想的。根据Kempton和Stewart［11］，重要持时与M有正的强相关性，重要持时随着M的增加而明显增加；重要持时与R有正的中度相关性，重要持时随着R的增加而增加。从3.1节、3.2节和3.4节分析来看，M和Rrup对DSFd的影响趋势基本与D5-95的相同。图5表明了M和Rrup对DSFd的综合影响。

如图5所示，当ξ＞5%时，在T＞1 s范围内，DSFd随着M的增加而减小；当ξ＜5%时，在更大的周期范围内，DSFd随着M的增加而增加。在长周期处，随着Rrup的增加DSFd偏离于单位1。此外，当ξ＜5%时，DSFd随Rrup的增加而增加；当ξ＞5%时，DSFd随Rrup的增加而减小；Rrup对DSFd的这种影响在较低的震级范围内更加明显。综合考虑M和Rrup可以较好地反映D5-95对DSFd的影响，所以在回归模型中可以采用M和Rrup两个参数来代替D5-95。

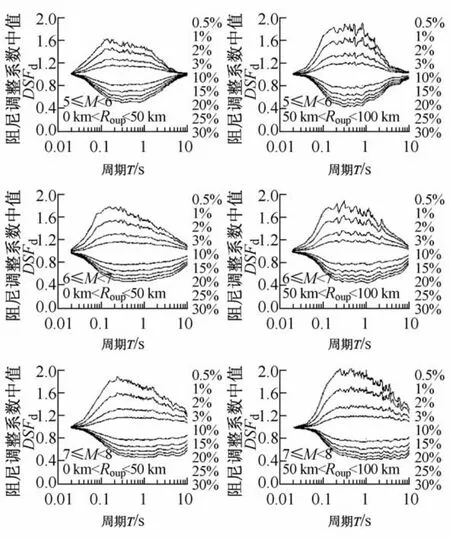
图5 M和Rrup对DSFd的影响Fig.5 Influence of M and Rrupon DSFd

6 结 论

（1）M对DSFd的影响与ξ，T有关，当ξ＜5%时，DSFd随M的增加而增加，ξ越小，T越大这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势；当ξ＞5%时，在T＞1 s的范围内，DSFd随M的增加而减小，ξ越大，T越大这种趋势越显著，在T＜1 s的范围内，这种趋势不显著，甚至有相反的趋势。

（2）近场地震动对DSFd无影响。在中远场Rrup对DSFd的影响与ξ，T有关，当ξ＜5%时，DSFd随Rrup的增加而增加，ξ越小，这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势；当ξ＞5%时，DSFd随Rrup的增加而减小，ξ越大，这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势。

（3）场地条件对DSFd的影响与ξ，T有关，ξ＜5%时，DSFd随Vs，30的增加而减小，ξ越小，这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势；当ξ＞5%时，DSFd随Vs，30的增加而增加，ξ越大，这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势。

（4）M对DSFd的影响显著；在本文研究范围内，Rrup对DSFd的影响较弱；场地条件对DSFd的影响微弱。

（5）D5-95对DSFd的影响与ξ，T有关，当ξ＜5%时，DSFd随D5-95的增加而增加，ξ越小，T越大这种趋势越显著，在短周期范围内，这种趋势不显著；当ξ＞5%时，DSFd随D5-95的增加而减小，ξ越大，T越大这种趋势越显著，在短周期范围内，这种趋势不显著，甚至有相反的趋势；D5-95是影响DSFd的一个重要因素。

（6）在回归模型中采用M和Rrup两个参数来代替D5-95可以较全面地反映D5-95对DSFd的影响。

［1］ Eurocode 8.Design of structures for earthquake resistance，part 1：general rules，seismic actions and rules for buildings［S］.Brussels，2004.

［2］ NEHRP-2003.Recommended provisions for seismic regulations for new buidings and other structures［R］.Washington D C：Federal Emergency Management A-gency，2003.

［3］ ATC-40.Seismic evaluation and retrofit of concrete building［S］.Redwood City：Applied Technology Council，1996.

［4］ FEMA-273.NEHRP guidelines for the seismic rehabilitation of buildings［R］.Washington D C：Federal Emergency Management Agency，1997.

［5］ FEMA-356.NEHRP pre-standard and commentary for the seismic rehabilitation of buildings［R］.Washington D C：Federal Emergency Management Agency，2000.

［6］ NEHRP-2000.Recommended provisions for seismic regulations for new buildings and other structures［R］.Washington D C：Federal Emergency Management Agency，2000.

［7］ Bommer J J，Mendis R.Scaling of spectral displacement ordinates with damping ratios［J］.Earthquake Engineering and structural Dynamics 2005，34（2）：145-165.

［8］ CameronW I，Green R A.Damping correction factors for horizontal ground motion response spectra［J］.Bulletin of the Seismological Society of America，2007，97（3）：934-960.

［9］ Stafford P J，Mendis R，Bommer J J.Dependence of damping correction factors for response spectra on duration and numbers of cycles［J］.Journal of Structural Engineering，2008，134（8）：1364-1373.

［10］ Lin Y Y，Chang K C.Effects of site classes on damping reduction factors［J］.Journal of Structural Engineering，2004，130（11）：1667-1675.

［11］ Kemptoma J J，Stewart JP.Prediction equations for significant duration of earthquake ground motions considering site and near-source effects［J］.Earthquake Spectra，2006，22（4）：985-1013.

Influence of the Damping Scaling Factor for Displacement Spectra

WANG Guotao*HU Kexu
（Reseach Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China）

848 ground acceleration records are orderly grouped according to momentmagnitude（M），distance to rupture plane（Rrup）and site conditions，respectively.Based on the classification，the influences of M，Rrup，site conditions and significant duration（D5-95）on the damping scaling factor（DSFd）are investigated.Consequently，there is a significant dependence between DSFdand M and a weak dependence between DSFdand Rrup.Site conditions influence the DSFdbut to amuch less degree than those of M and Rrup.D5-95is an important factor controlling the DSFd.The effects of the M，Rrup，site conditions and D5-95on DSFddepend on the damping ratio（ξ）and period of vibration（T）.The DSFddecreases as M，Rrupand D5-95increases at long periods ifξ＞5%.The pattern with M，Rrupand D5-95ismuch more significant if T is longer orξis larger.The DSFdincreases as M，Rrupand D5-95increases atmore range of periods ifξ＜5%.The pattern with M，Rrupand D5-95ismuch more significant ifξis smaller.Almost no pattern with M，Rrupand D5-95is seen at shorter periods.The effects of D5-95on DSF can be captured by including Rrupas one of the predictor variables in the regression model in addition to M.

moment magnitude，distance to rupture plane，site condition，significant duration，damping scaling factor for displacement spectra

2013－04－03

*联系作者，Email：802212wgt＠tongji.edu.cn