拥挤效应、经济增长与城市规模

王 俊

（1．华中科技大学 经济学院，湖北 武汉 430074；2．湖南科技大学 商学院，湖南 湘潭 411201）

拥挤效应、经济增长与城市规模

王 俊1，2

（1．华中科技大学 经济学院，湖北 武汉 430074；2．湖南科技大学 商学院，湖南 湘潭 411201）

本文运用新古典经济的框架建立了一个经济增长模型，系统分析了拥挤效应、经济增长与城市规模的关系。假设城市规模扩大产生集聚效应并反映为拥挤效应的降低，将拥挤效应作为影响经济增长的因素纳入生产函数，分析经济稳态的演化路径，得出最优的城市规模、合理的城市拥挤程度和稳定的经济增长速度，并分析扰动稳态的变量对演化路径的影响，据此给出了一个估算最优城市规模的简单模型的结论。研究表明在不同条件下城市的最优规模是可变的，不存在统一的最优城市规模，城市化进程应该适度有序的进行。

城市规模；拥挤效应；经济增长

一、引言

改革开放以来，我国经历了三十多年的快速城市化历程。2010年城市化率达到49．52%，其中北京、上海、广州和深圳的人口均超过千万，如北京全市人口达1961．24万，城区内居住人口1556．32万，上海全市人口2301．91万，城区内居住人口1764．08万。①如此庞大的城市规模远超过城市规划者和设计者的预期，因此我国的城市问题显得特别突出。目前城市普遍面临着交通拥堵、房价偏高、环境问题严重、城市治理成本增加、投资效率下降等一系列的“城市病”。这些城市问题产生的原因一方面是城区内市政规划有问题，如市内各功能区规划不合理，交通网络设施设计不合理等，这主要体现在中小城市；另一方面是人口规模从根本上超出了城市的最佳承载能力，这主要体现在大城市。

有学者分析，我国城市化率如要达到高收入国家78%的规模还需提高30个百分点，这意味我国城市人口还需增加近4亿的数量，加上我国同时面临特大城市人口过度集中和大部分中小城市规模发展不足的问题，[1][2]因此优化城市的合理规模，避免大城市的盲目扩张，挖掘中小城市扩容的潜力等问题对于我国显得尤为重要。

二、文献综述

国外对传统城市规模的研究主要从成本收益的角度出发，认为最优城市规模应是实现总社会福利或人均社会福利最大化的人口规模，或是使公共服务的平均成本最小的人口规模，或是使生产成本最小的城市规模。[3][4]国内学者王小鲁和夏小林用规模收益递增生产函数表示城市经济集聚的收益，用政府和居民负担的外部成本函数之和来表示城市的总外部成本，认为最优城市规模应以居民意义上的平均净收益最大化为准则；[5]李秀敏等在此基础上，在测算城市外部成本时增加了企业成本，认为当城市总收益等于总成本时，城市处于发展的临界阶段，当净收益最大时，城市处于最优规模；[6]还有些学者从环境约束的角度来研究城市规模。周海春等认为城市适度人口规模取决于经济发展对人口的需求和资源、环境、社会发展对人口规模的制约；[7]许抄军等从城市资源制约和环境质量的角度来研究中国城市的最优规模;[8]包正君等认为我国现阶段出现城市问题的原因是快速城市化引起的人口集聚和人口的盲目集中使城市人口规模超过了城市生态环境的人口承载量。[9]

国外对新地理经济学的研究主要集中在以下两个方面。一是集聚经济与经济增长的互动机制，主要将集聚导致的垂直关联和移民、人力资本与实物资本的流动和知识溢出、熟练工人迁移与知识创新、贸易与创新成本、差异化产品贸易等因素纳入内生增长的框架，研究城市集聚对经济增长的作用，以及集聚与增长的循环累积效应。[10][11][12][13]二是拥挤效应与规模经济的权衡机制，认为最优城市规模是城市集聚过程中外部经济和外部不经济权衡的结果。[14]外部不经济即为拥挤效应，体现为交通上的拥挤程度、通勤成本、边际地租等;[15][16]外部经济即为规模经济，城市集聚的规模经济的微观基础主要体现在共享、匹配和学习机制。[17]另外，还有学者提出了“有效城市规模”的概念，把单个城市视为整个城市分工网络上的节点，强调了城市间的网络外部效应。国内学者对此也有研究，如安虎森等通过最大化实际收入研究最优城市规模，得出只有当黑洞条件满足时才存在最优城市规模的结论，而且最优城市规模还取决于农产品的贸易成本。[18]肖文等在新地理经济学的框架下研究了外部规模经济、拥挤效应与城市规模的关系。[19]

综上所述，从成本收益的角度研究城市问题是一种微观且局限的方法，不能反映城市作为一个系统性的组织结构的整体机理。新地理经济学则主要强调地理空间在城市演化中的影响，重点分析城市最优规模的微观基础。将拥挤效应、城市规模和经济增长三者结合起来的研究相对较少，如Esteban和Mark构建了一个内生增长模型进行了分析尝试；[20]张应武从城市经济增长的角度估计了中国城市的最优规模，认为城市规模与经济增长之间是非线性关系，存在一个促进经济增长的最优城市规模；[21]王家庭从生态约束的角度构建内生增长模型来分析最优城市规模。[22]本文正是在此基础上拓展了拥挤效应的概念，认为拥挤效应不仅体现在生态环境约束和交通拥挤上，也体现在导致资源配置下降的各种因素上，如投资的边际效率的降低、城市治理成本的上升、房价等生活成本的上升等等。通过构造拥挤效应函数，将其纳入生产函数，建立一个经济增长模型，分析最优规模的演化路径及其影响因素，为不同条件下的城市最优规模估算提供一个理论参考。

三、最优城市规模模型的构建

（一）城市规模与拥挤效应

城市规模是衡量城市大小的数量概念，包括城市人口规模、用地规模、经济规模、基础设施规模，这四方面是互相联系又互相区别的。通常将人口作为衡量城市规模的决定性指标，但由于人口数量与实物资本存量可以视为按一定的比例匹配，因此为了便于分析，本文将城市规模（G）的大小用城市的实物资本存量（K）来代表，一般而言，城市规模越大资本存量越大，当城市规模发展到一定程度后，城市的集聚效应降低，而城市的拥挤效应增强，所以假设城市拥挤效应的产生函数为：

其中Bk〉0、Bkk〉0，这表示拥挤效应对实物资本的一阶二阶导数均大于零，意味着拥挤效应随着城市规模的扩大而加速增加。假设拥挤效应会因为城市的集聚效应而减弱，以a的速度下降，则城市拥挤效应的运动方程为：

其中当城市达到最优规模时，拥挤效应和集聚效应相互抵消，即经济系统达到长期稳定的状态，则Z˙=0，此时，根据式（2）可以得到：

在式（3）中dZ/dK=Bk/a〉0、d2Z /d2K=Bkk/a〉0，可以得到当长期均衡时，曲线Z˙=0的形式如图1所示，当B（K）〈aZ时，Z˙〈0，Z位于曲线的上面，此时Z必定下降；反之，当B（K）〉aZ时，Z˙〉0，Z位于曲线的下面，此时Z必定上升。

（二）生产函数与经济增长

为了简化分析，不考虑城市规模产生的拥挤效应对于生产函数的影响，假设产出是关于资本存量的函数，也不考虑人口和技术的影响，这里假设人口的影响隐含在实物资本存量中，技术进步不仅影响产出，也降低拥挤效应，这里暂不作考虑，则生产函数可以设为：

根据边际报酬递减规律，有Fk〉0，Fkk〈0。为了简化分析，假设人口的增长率和技术进步率均为零，则净资本存量的积累等于储蓄减去折旧，即

其中s为储蓄率，δ为折旧率。当经济系统达到长期均衡时，K˙=0，此时sF（K）=δK，对应着经济稳态时最优的资本存量，曲线K˙=0的形式如图1所示。当sF（K）〉δK时，K˙〉0，K位于曲线左侧，此时K必定向右移动至；反之，当sF（K）〈δK时，K˙〈0，K位于曲线的右侧，此时K必定向左移动至。

如果考虑拥挤效应对生产函数的负作用，则生产函数改写为：

其中dQ /dZ〈0，d2Q /d2Z〈0，因为城市的拥挤效应对生产有负的作用，并且产量随着拥挤效应的增加而加速下降，生产函数中实物资本的边际产出与拥挤效应无关。

（三）演化路径与均衡

分析模型的动态均衡须考虑上述两种情况。第一种情况是当拥挤效应不影响经济增长时，联立方程式（2）和（5），且两方程同时满足=0和=0，从图1上可以看出均衡点位两条曲线的交点。方程B（K）=aZ和方程sF（K）=δK同时满足，可以求解得到稳态时的和Z*。当≠0和≠0时，根据前面的分析，非均衡的位置叠加运动方向，会沿着箭头的方向沿虚线收敛于均衡时的状态，因为拥挤效应和资本存量相互影响。

第二种情况是考虑拥挤效应对经济增长的负作用时，联立方程式（2）和（7），且两方程同时满足=0和=0，从图2可以看出均衡点位两条曲线的交点。方程B（K）=aZ和sF（K，Z）=δK同时满足，可以求解得到稳态时的K*和Z*。根据两个方程的路径叠加后可以将图2分为8个区域，即用水平线和垂直线将=0和=0两条线分的4个区域再分别分成2个区域，区域①③⑤⑦可以直接根据虚线的路径收敛于稳态，但是区域②④⑥⑧的位置不能直接收敛于稳态，而是分别移动到对应的③⑤⑦①区域内，然后再沿虚线收敛。以区域②为例，在此区域内〉0，因为城市规模较大，导致拥挤效应增加，即向上移动，但是此时拥挤效应已经高于稳态的拥挤效应，所以不可能直接收敛于稳态，另外，又因为〈0，此时因为挤出效应使得储蓄低于折旧，导致实物资本减少，城市规模减小，即向左移动，综合起来在②区域内的点会向左上方移动至③区域，在③区域内，根据前面分析的原理会向左下方移动，沿虚线收敛于稳态。

图1 稳态的演化路径（无拥挤效应的生产函数）

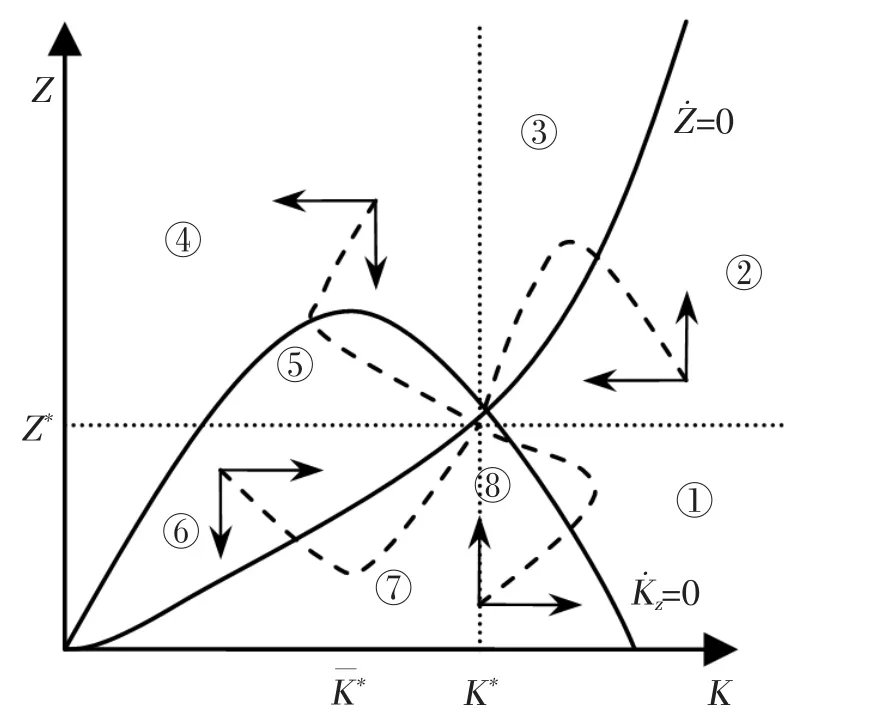
图2 稳态的演化路径（有拥挤效应的生产函数）

比较两种情况的稳态水平可以发现，当考虑拥挤效应对生产函数的影响时，均衡时的实物资本存量和拥挤效应均低于不考虑拥挤效应的情况，因此最优的城市规模也相对小一些，居民的生活也更舒适，并且两种情况都收敛于稳态，说明经济增长的速度相同，所以将拥挤效应纳入生产函数更为合理和有效。综上所述可得到：

命题1：长期来看，无论城市的拥挤效应是否影响生产函数，实物资本存量和经济增长速度均收敛于稳态，城市规模均收敛于最优城市规模。稳态时，城市聚集产生的正效应等于拥挤产生的负效应。

四、最优城市规模影响因素的分析

（一）影响因素与均衡

命题2：短期的外生冲击（基础设施的改善、绿化面积的增加、交通条件的改善和一些其他的引导政策）会影响长期经济均衡的位置，改变城市的最优规模，减少拥挤效应的措施会扩大城市最优规模。

根据公式（7），影响经济增长的外生变量主要是储蓄率s和折旧率δ，s的下降或δ的增加都会使资本存量减少、经济规模缩小，在图3中可以理解为=0向左下方移动至=0，初始均衡点Q1移至Q3，参数变化后在Q1的位置出现图2中区域③的情况，即沿虚线收敛于新的均衡位置Q3，反之，s的增加或δ的下降都会使得资本存量增加、经济规模扩大。

不同大小或不同区域的城市由于生活习惯、文化差异、收入水平、地理位置等差异，储蓄率s和折旧率δ是不一致的，因此这些条件的改变都会影响到最优城市规模的改变，并且稳态的城市拥挤程度和经济增长速度都会发生改变。

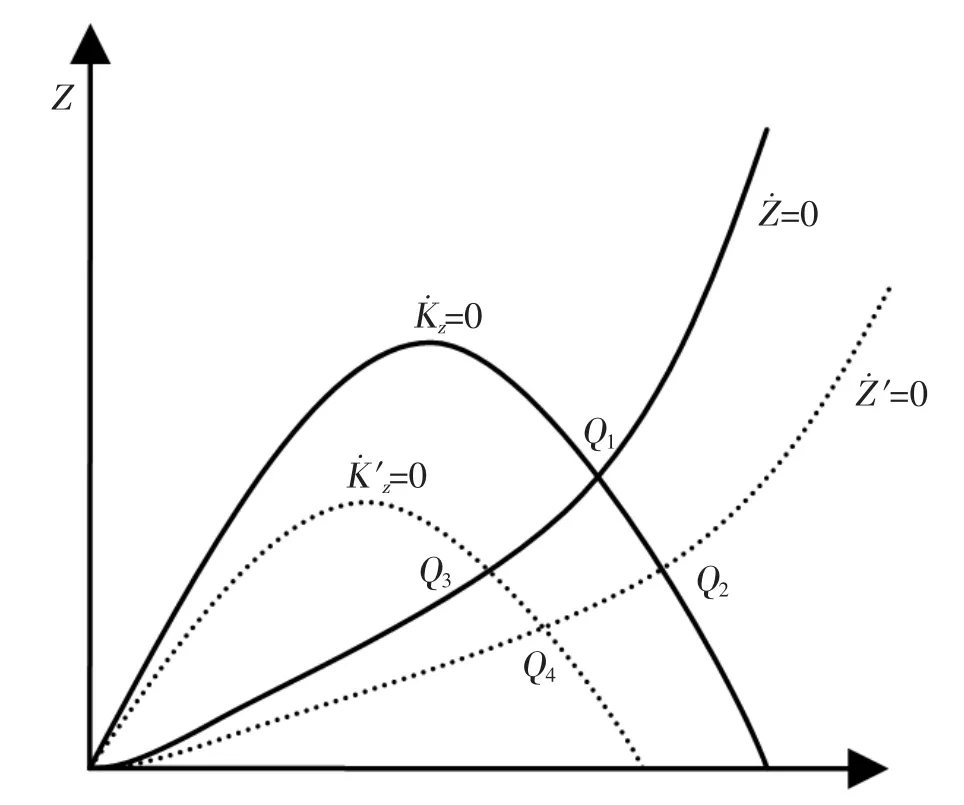
图3 稳态的比较静态分析

经济系统中，影响上述两个均衡方程的参数可能同时发生变化，当城市集聚产生正效应时，a增加，拥挤效应下降，曲线=0往右下方转动，同时，s的下降或δ的增加都会使得资本存量减少，经济规模缩小，在图3中可以理解为=0向左下方移动至=0，均衡位置从Q1移至Q4，表现为最优城市规模的缩小。Q1相对于Q4而言，相当于图2中③或④的位置，收敛路径分别为图2中的虚线所示。其他的参数变化可以按同样的原理进行分析。

根据上述分析，命题2中的短期外生冲击对拥挤效应的影响以及内生或外生的影响因素会使得储蓄率s和折旧率δ产生改变进而影响经济增长，这些参数会因为不同城市规模和不同时期而改变，具有一定的不稳定性，所以最优城市规模也会随之改变。因此可以总结得到:

命题3：横向而言，不存在统一的最优城市规模，不同等级的城市都有其不同的最优城市规模；纵向而言，城市的最优规模是一个动态的过程，随着时间变化和不同的外部条件而改变。

（二）均衡模型的简单设定

为了能够量化分析，可以对前面分析框架的经济函数和参数进行设定，考虑函数的便捷性，这里设定的每个函数仅满足最基本要求的简单形式。

假设城市规模和大部分的分析保持一致，用人口数量N来替代城市规模G，根据经验，人口数量和资本存量并不是线形关系，因为资本存量可以无限增加而人口数量却不能，所以设定两者之间为线形对数关系，具体为：

其中h为人口数量对资本存量的弹性系数，且1〉h〉0，它也可以理解为资本增量和人口数量的变动率之间的匹配关系。拥挤效应因为人口的聚集而产生，也可以设定为：

其中i为拥挤效应对于人口数量的弹性系数，且1〉i〉0，将公式（9）和（10）代入公式（2）可以得到城市拥挤效应增加函数为：

另外，根据公式（6）的假设条件，拥挤效应对产出表现出负的效应，可以设定生产函数为：

其中1〉α〉0，β〉0。将公式代入（7）式可以得到：

联立式（12）和（15）可以求得均衡的最优城市规模的资本存量和拥挤程度分别为：

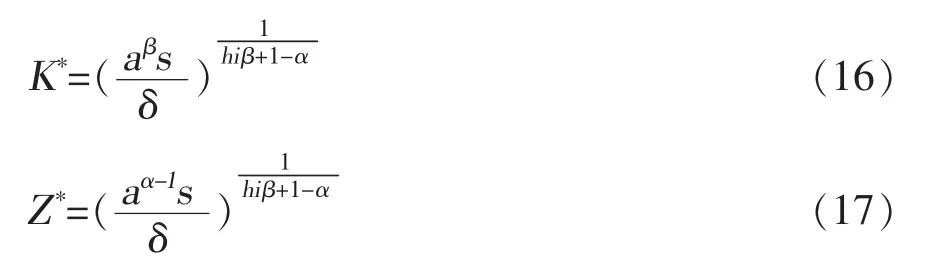
此时，根据式（9），均衡时最优城市规模为：

为了方便分析，可以对（18）式取对数得到：

对（19）式变换可以得到：

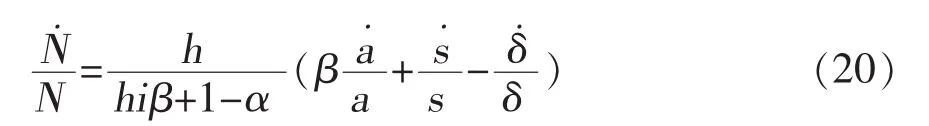
从（20）式可知，最优城市规模与集聚效应的增长率和储蓄率的增长率正相关，和折旧率的增长率负相关，但是后两者在现实经济中短期内可以假设是不变的，因此当城市达到最优规模后，其增长关键仍取决于集聚效应增长。从模型分析中我们知道集聚效应可以降低拥挤效应，拥挤效应的降低促进产出的增长，产出增长会增加资本存量，资本存量增加导致人口的集聚，城市最优规模增长，所以最优城市规模的增长率与其集聚效应增长率正相关的结论完全符合模型的设定。

从均衡的结论可以看到，参数对城市规模的影响满足模型框架的分析结论，因此也可以用此结论对我国城市规模进行简单的估算。如果要分析更多的城市问题，对上述函数和参数进行重新设定依然可以进行。因为数据获取的困难，这里暂不进行估算，仅提供一个估算的理论方法，不同等级的城市规模其模型中参数是不一致的，所以最终估算出的大城市和中小城市的最优规模也将不一致，这是符合实际的。城市化进程应该与工业化进程匹配，城市化超前将出现所谓的“鬼城”，城市化滞后将出现城市过度拥挤，都不是资源的最优配置，所以城市化进程要适度且有序地展开。

五、结论

城市规模的扩大会产生较强的集聚效应，如规模经济、关联效应、技术创新、知识溢出等外部经济，但是随着城市规模扩大到一定程度则会出现边际收益的递减，而拥挤效应则出现边际负收益的递增，最终当拥挤带来的损失超过规模扩大带来的收益时，经济就缺乏效率，如果没有政府的干预，城市规模的扩张是不可能持续的。本文在新古典经济的框架下构建了一个经济增长模型，系统分析了拥挤效应、经济增长和城市规模的关系，为分析最优城市规模的估算提供了一个理论依据。

首先，模型的建立在于构建一个城市拥挤效应函数，城市拥挤效应随着城市规模的扩大而增加，城市规模扩大产生的集聚效应的正效应反映为拥挤效应的减少，形成一个拥挤效应增量与城市规模的函数。其次，对于经济增长而言，构造一个生产函数，将城市规模用实物资本存量表示，可以认为产出是相对于城市规模的增函数；并分析了经济增长收敛的稳态过程，而且将拥挤效应也纳入生产函数，分析其稳态的收敛过程，通过比较研究的方法可以得到一个结论，即无论拥挤效应是否被纳入生产函数，经济增长都会收敛于稳态，因此城市的最优规模是存在的。再次，通过对模型参数的变化分析了其对于经济稳态的影响，得到城市最优规模是可变的结论，不仅反映在不同经济规模的最优城市规模不同，也反映在不同时期的最优城市规模的变动。最后，本文还给出了一个简单的最优城市规模的估算模型，得出最优城市规模的增长率取决于其集聚效应的增长率。所以，政府在促进城镇化过程中应根据城市的实际情况控制城市规模，主要通过增加集聚效应或降低拥挤效应来扩大城市规模。

本文的模型存在一些不足之处，例如没有对储蓄率内生化、没有研究家庭的消费和政府的政策对均衡产生的影响。另外，我国下一阶段城市化的方向主要是中小城市扩容、增加大城市的数量、改善城市规模结构、优化城市空间布局等。为解决这些问题，对我国不同规模、不同区位、不同功能的城市最优规模测度的研究非常迫切和重要，这些研究都可以在本文的模型基础上进一步进行。

注 释：

① 数据来源于《中国2010年人口普查资料》。

② 数据来源于《2011年中国区域经济统计年鉴》。

[1]王小鲁．中国城市化路径与城市规模的经济学分析[J]．经济研究，2010，（10）:20-32．

[2]简新华,黄锟．中国城镇化水平和速度的实证分析与前景预测[J]．经济研究，2010，（3）:28-39．

[3]Amott R．J．,J．E．Stiglitz．Aggregate Land Rents,Expenditure on Public Goods,and Optimal City Size[J]．The Quarterly Journal of Economics,1979，（4）:471-500．

[4]Evans A．W．A Pure Theory of City Size in an Industrial Economy[J]．Urban Studies,1972，（9）:49-77．

[5]王小鲁,夏小林．优化城市规模 推动经济增长[J]．经济研究,1999，（9）:22-29．

[6]李秀敏，刘冰，黄雄．中国城市集聚与扩散的转换规模及最优规模研究[J]．城市发展研究，2007，（2）:76-87．

[7]周海春,许江萍．城市适度人口规模研究[J]．数量经济技术经济研究，2001，（11）:9-12．

[8]许抄军,基于环境质量的中国城市规模探讨[J]．地理研究，2009，（3）:792-800．

[9]包正君,赵和生．基于生态足迹模型的城市适度人口规模研究——以南京为例 [J]．华中科技大学学报 （城市科学版），2009，（2）:84-89．

[10]Black D．,Henderson V．A Theory of Urban Growth[J]．Journal of Political Economy,1999，（2）:252-284．

[11]Fujita,M．and J．Thisse．Economics of Agglomeration: Cities,IndustrialLocation,and RegionalGrowth[M]．Cambridge University Press,2002．

[12]Martin,P．and G．Ottaviano．Growth and Agglomeration [J]．International Economic Review，2001，（42）:947-968．

[13]Yamamoto K．Agglomeration and Growth with Innovation in theIntermediate [J]．RegionalScienceand Urban Economics，2003，（3）:335-360．

[14]Henderson J．V．Economic Theory and the Cities[M]．New York Academic Press,1977．

[15]Dixit A．The Optimum Factory Town[J]．Bell Journal to Economics，1973，（4）:637-654．

[16]Mills E．S．,Beeker C．M．Studies in Indian Urban Development[M]．Oxford University Press,1986．

[17]Duranton G．,D．Puga．Micro-Foundations of Urban Agglomeration Economies[C]．J．V．Henderson,J-F．Thisse (eds．)Handbook of Urban and Regional Economics．Amsterdam,North Holland,2004，（4）．

[18]安虎森,邹漩．最优城市规模选择与农产品贸易成本[J]．财经研究,2008，（7）:74-97．

[19]肖文,王平．外部规模经济、拥挤效应与城市发展:一个新经济地理学城市模型[J]．浙江大学学报(人文社科版)，2011，（3）：94-105．

[20]Esteban and Mark．Urban Structure and Growth [J]．Review of Economic Studies,2007，（74）:597-624．

[21]张应武．基于经济增长视角的中国最优城市规模实证研究[J]．上海经济研究，2009，（5）:31-38．

[22]王家庭．生态环境约束对城市化的影响:基于最佳城市规模模型的理论研究[J]．学习与实践，2011，（1）:5-17．

（责任编辑：彭晶晶）

Congestion Effects，Economic Growth and City Size

WANG Jun1,2
（1．School of Economics,Huazhong University of Science and Technology,Wuhan Hubei 430074,China;2．School of Business, Hunan University of Science and Technology,Xiangtan Hunan 411201,China）

In the framework of neoclassical economics,this paper established an economic growth model,and made a systematic analysis of the relationship between congestion effects,economic growth and city size．Through constructing a congestion effects function caused by expansion of city size,we showed that expansion of city size can generate agglomeration effect, which are reflected as a decrease of congestion effects,Meanwhile,congestion effects can affect economic growth by entering the production function,In addition,by analysis of the evolution path of steady-state economic,we solved for the optimal city size,a reasonable congestion degree and the stable economic growth rate,and then explored the evolution path affect imposed by the factors which may disturbance steady state．Finally,we gave a simple model to estimate the optimal city size．According to the analysis of this model,our paper showed that the optimal city size is variable under different conditions,and there is no unified optimal city size．Therefore,the process of urbanization should be moderate and orderly．

city size;congestion effects;economic growth

F124

A

1672-626X（2014）01-0046-07

10．3969/j．issn．1672-626x．2014．01．008

2013-11-07

教育部人文社科基金青年项目(12YJC790186);教育部人文社科重大课题攻关项目(11JZD018)

王俊（1978-），男，湖北应城人，湖南科技大学讲师，华中科技大学经济学院博士研究生，主要从事人口资源与环境经济研究。