基于FEM/BEM的浸水结构振动及声辐射特性国内研究综述
王峥,洪明,b,刘城(大连理工大学.船舶工程学院;b.工业装备结构分析国家重点实验室,辽宁大连116024)
基于FEM/BEM的浸水结构振动及声辐射特性国内研究综述
王峥a,洪明a,b,刘城a
(大连理工大学a.船舶工程学院;b.工业装备结构分析国家重点实验室,辽宁大连116024)
文章基于有限元(FEM)或有限元结合边界元(FEM/BEM)分析方法,对浸水结构振动及声辐射特性国内公开发表的文献进行梳理,从低频流固耦合的振动特性、弱耦合与强耦合的声辐射特性、直/间接边界元的非唯一性与奇异性等着重流体数值模拟方面,对国内相关研究进行了综述分析,就浸水结构振动及声辐射特性的研究发展动态做出了总结,为相关科研人员研究浸水结构振动特性及声辐射提供了有益参考。
有限元;直接边界元;间接边界元;流固耦合;声辐射;非唯一性;奇异性
1 引言
若结构在流体中振动,则流体与结构之间存在相互作用,相应称为流固耦合问题。根据耦合的强弱可以采用不同的分析模型。结构与低密度流体介质是弱耦合,对于介质中结构的振动特性及声辐射问题可分别求解,先计算出结构的振动响应,辐射声场可以通过结构的振动响应来确定。对于研究浸水结构的振动特性及声辐射问题,一般在物理上视为结构与重流体介质耦合,对此强耦合系统振动响应和水中声场必须耦合求解。以振动板壳声振耦合研究为例,耦合的强弱可用特征量λ来判别[1]:

其中:c是声在介质中传播速度;ρ是结构质量密度;h是板厚度;ω是结构与流体耦合系统振动频率。当λ<1时,认为系统是弱耦合;当λ>1时,认为系统是强耦合。
当浸水结构在低频振动时,流体对结构的作用可看成是附加质量效应;而高频时流体的阻抗相当复杂,包括质量与阻尼两方面的影响。一般低频时可用有限元(FEM)或有限元和边界元(FEM/BEM)相结合来研究结构在流固耦合作用下的振动及声辐射特性,而在高频时则用统计能量分析方法(SEA)来研究。
考虑到篇幅综述文献限于结构满足线弹性基本假定;对流体假定为理想流体且无旋,在线性小扰动的情况下的声辐射,而且流体区域讨论的范围限定于无限或半无限三维空间。若流体假设为可压缩的,则声压或速度势满足Helmholtz方程,若将流体假设为不可压缩的,则声压或速度势满足Laplace方程。当研究结构声辐射问题时,考虑到声音在介质中传播的速度不能为无限大,所以假设流体是可压缩的;仅对于流固耦合作用下结构低频振动的计算,则可假设流体是不可压缩的,分析模型简单且精度可以接受。
无论是求解流固耦合振动特性问题还是声辐射问题,由于结构和流体的相互作用,所以要考虑到结构运动方程与流体运动方程的耦合方式。如果将结构利用有限元理论进行处理,流体利用边界元理论进行处理,则其耦合方式有两种:第一种是将流体的边界积分方程耦合到结构的运动方程中,进而求解有限元方法离散得到的运动方程;第二种是将结构的运动方程耦合到流体的Helmholtz微分方程或Laplace微分方程中后,将Helmholtz微分方程或Laplace微分方程转化为积分方程来进行求解未知变量。显然,第一种方法是利用边界元的基本原理对流体进行降一维处理,而第二种方法由于方程耦合过程中导致了Helmholtz微分方程或Laplace微分方程中的主要变量发生变化,其后续处理的积分形式也发生变化,致使处理十分困难,所以一般利用结构有限元结合流体边界元理论对流固耦合问题进行处理时选用第一种方式。如果结构和流体都利用有限元理论来处理,考虑到结构和流体的相互作用,其结构运动方程与流体运动方程同样存在类似的耦合方式,只是无论哪种耦合方式对于结构还是流体涉及到的积分并不能进行降维处理。
2 结构有限元与流体边界元理论梗概
2.1 有限元理论
对于弹性体结构采用有限元法计算其振动特性是非常方便的,相应的振动运动方程如下:

其中:M为系统的质量阵;C为系统的阻尼矩阵;K为系统的刚度阵;Fs为作用在结构上激励力矢量。
若计算结构的固有振动特性,忽略阻尼,则方程变为:

2.2 直/间接边界元(D-BEM/I-BEM)理论
假设流场为无旋、可压缩且做小扰动运动,线性齐次声学波动方程满足Helmholtz微分方程:

其中:p为流体动压力;k=ω/c为波数;ω为圆频率;c为流体介质中的声速。
假设流场为无旋、不可压缩且做小扰动运动,则c→∞,Helmholtz微分方程简化为Laplace微分方程:

对振动结构在无限流体域中声辐射的数值模拟,通常是将流体域中控制微分方程(Helmholtz微分方程)转化成边界上的积分方程,然后采用直接或间接边界元法进行数值计算。直接边界元方法理论的Helmholtz积分方程是基于封闭结构建立,且内场外场问题分别是不同的分析模型,如图1所示。
其Helmholtz积分方程如下:内场问题:
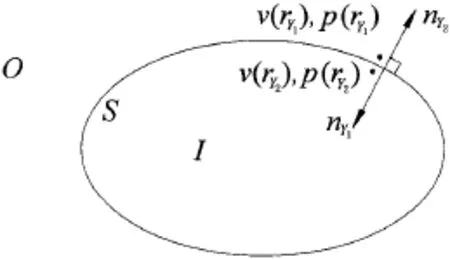
图1 直接边界元法主要变量示意图Fig.1 Primary variables of D-BEM

其中:p为场点声压;rX为场点的位置矢量;G为Helmholtz方程的Green函数;GL为Laplace方程的Green函数;C1(rX)和C2(rX)分别为内外场问题的边界积分系数;S为结构表面,无论是内场问题还是外场问题,当P∈S时C1(rX)或C2(rX)的表达式适用于任意形状的结构表面;当S为光滑表面时,C1(rX)或C2(rX)的值均为1/2。
直接边界元理论的Helmholtz积分方程的求解是将边界离散后,利用配点法来计算结构表面未知变量,然后利用内外场问题的公式(6)和(7)等来计算场点声压、辐射声功率及声辐射效率等物理量。
对于结构向三维半空间内进行声辐射,并且结构可以简化为镶嵌在无限大刚性障板中的问题,直接边界元法理论的Helmholtz积分方程可简化为Rayleigh积分形式:

其中:p为半空间介质中或结构表面上的任意点声压;S为结构表面。Rayleigh积分可看成是直接边界元法理论的Helmholtz积分方程的特殊形式。

图2 场点在结构封闭域外Fig.2 Field point P in the exterior acoustic domain
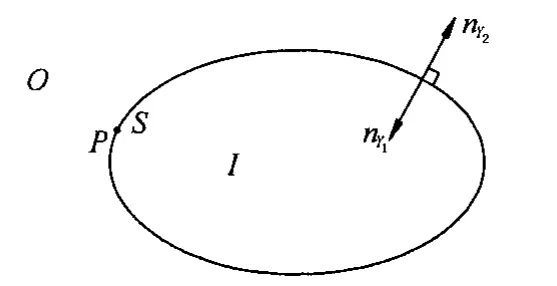
图3 场点在结构边界上Fig.3 Field point P on the boundary
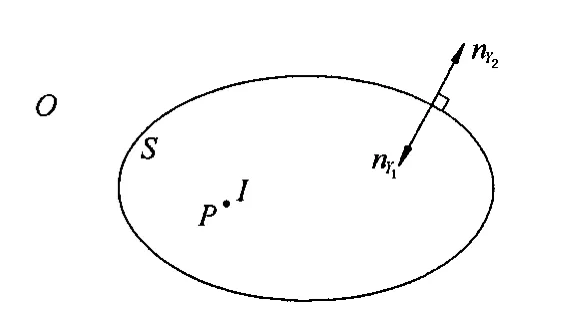
图4 场点在结构封闭域内Fig.4 Field point P in the interior acoustic domain
间接边界元法理论是利用直接边界元理论内场和外场的边界积分公式推导得到的。如图2-4所示,结合直接边界元法的理论计算公式可得出结论,无论场点P是在声场域中任意位置都有:

由公式(6)和(7)相加结合公式(9)可得声场域中任意点的边界积分公式:
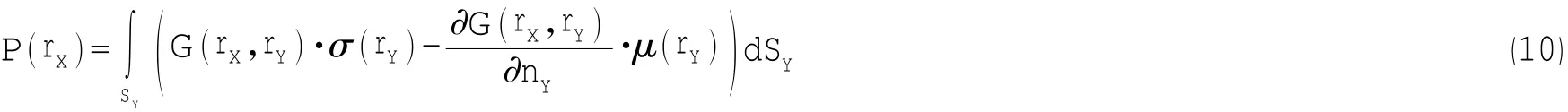
由于间接边界元理论推导所涉及的主要变量为振动结构边界表面的声压差和声压梯度差,由公式(10)可看出,求出结构边界表面的声压差和声压梯度差便能得到辐射场,所以必须将场点分别移动到边界的两个表面上,进而推导出结合了边界条件的边界积分公式,才能进一步求得结构边界表面的声压差和声压梯度差。比如,假设声场满足Neumann边界条件,则推导出的结合了边界条件的间接边界元理论的Helmholtz积分方程为:

其中:ρ为介质密度;nX为声场边界场点的法线方向与nY方向规定相同;)为声场边界的速度边界条件。
间接边界元理论的Helmholtz积分方程离散后,边界单元上未知的主要变量可以用形函数插值单元节点上的值来表示,但是其不能像直接边界元那样利用配点法来计算边界表面的未知变量,而普遍的求解方法是利用变分原理来进行边界表面未知变量的求解。比如对于Neumann边界条件,最终得到的泛函方程为:

其中:Q为系统矩阵,其为对称阵;μ为结构表面节点上未知变量的列向量;b为边界上速度推导的列向量。
利用变分原理,公式(12)可得:

对于Neumann边界条件,可通过求解方程(13)得到结构边界表面的声压差,从而求得场点声压、辐射声功率以及声辐射效率等物理量。
2.3 有限元方法或有限元与边界元结合方法计算浸水结构振动及声辐射特性运动方程
对于浸水结构振动及声辐射特性的求解,无论是利用FEM或FEM/BEM结合理论,终归于对耦合的运动方程进行求解,耦合流体后的结构运动方程为:

其中:Fa为流固交界面作用在结构上流体动压力矢量,流体动压力Fa是一个复数,从物理上解释体现为流体对结构的作用力,其可以等效为对结构的惯性力以及阻尼力的影响,其中的惯性力也就是对结构的附加质量效应(对应Fa的实部),阻尼力也就是对结构的阻尼效应(对应Fa的虚部)。在激励力频率较低的低频区域,流体对结构的作用主要表现为附加质量效应,对结构的阻尼的影响很小。也就是说作用于结构湿表面的流体动压力可以近似转换为结构动力学方程的加速度项。这样如果只考虑激励力的频率是在中低频的范围内,那么最终水下结构的动力学方程可转换为如下的形式:

其中:Ma为浸水结构的附加质量阵。当研究进水结构固有振动特性时Fs为零,忽略阻尼,上式对应的广义特征值问题为:

3 国内浸水结构振动及声辐射特性研究现状
3.1 浸水结构振动特性研究现状
对于浸水结构振动特性的研究,包括浸水结构低频振动时的附加质量阵、浸水结构在流固耦合作用下的振动特性计算以及相关实验的研究。
3.1.1 浸水结构低频振动时的附加质量的研究
对浸水结构的附加质量阵Ma的研究是求解浸水结构振动及声辐射特性的基础,其能体现出流固耦合的相互作用效应,Ma的求解过程也是求解浸水结构振动及声辐射特性的难点所在。对于研究附加质量阵的计算方法,可以用有限元的理论直接将流体域进行离散,也可以用边界元的理论将三维流体域降一维再对边界进行离散计算。无论是哪种对于流体的处理方法,Ma的推导思路基本相同,首先是对Helmholtz微分方程公式(4)或Laplace微分方程公式(5)进行三维或二维域内积分并变换得到三维有限域积分方程或边界积分方程,将流体动压力Fa用其积分后的式子来表示,此时流体动压力Fa是ω2的函数,这样Fa就可以与(14)式中的质量阵M合并,此时称Fa中可以与质量阵M合并的矩阵即为附加质量矩阵Ma,它的意义是接触面上结构振动加速度引起流体压力的附加值。也就是说对于附加质量阵的研究,就是对于流体动压力Fa的研究。
将无限流体域截断为有限流体域,将有限域流体和结构都利用有限元进行数值模拟,即结构有限元耦合流体有限元(FEM/FEM),这种方法基本思想是将公式(4)或公式(5)在有限体积域内积分,将积分后的表达式进而转化成流体动压力Fa的形式,进而求得附加质量矩阵Ma,这是比较常用的处理流固耦合问题附加质量的方法,其难点在于流体截断域的选择、流体有限元的划分以及流体单元类型的选择等。汪庠宝和韩继文等[2-3]对悬臂板和连续板的流固耦合振动,给出了浸水结构的附加质量有限元法的计算格式,其对于板格在不同的边界条件约束下的附加质量系数进行了研究。裴智勇和吴卫国等[4]对高速船舱壁加筋板流固耦合振动问题,将结构有限元法和流体有限元法结合,根据Garlerkin法和Hamilton变分原理分别推导出离散的流体和结构的运动方程,推导出流体附加质量矩阵。文献[5-6]同样利用有限元方法离散流体的思想,早期研究人员多基于有限元方程编制相应数值计算程序进行计算。对于这类方法,可用于几何形状相对较简单结构附加质量阵的求解,其优点是方程的理论推导及数值实现相对简洁,对一些有可能存在规律性结果的问题进行研究比较有益;其缺点是一旦结构比较复杂,其流体划分有限元就比较复杂,单元和节点增多,导致计算量比较大。
对流体动压力Fa来说,针对理想流体流场可用速度势来表示,域中速度势满足Laplace方程,对于这类流场可使用源汇分布法(Green函数法)讨论结构物与周围流体的稳态相互作用问题。可求出流场中任一点的速度势,进而求出流体的动压力,从而求解附加质量阵。王国强和杨建民[7]利用结构有限元模型,结构湿表面上布置源汇来模拟流体,采用线性三角形源汇法与结构有限元模型相结合的办法计算出了振动结构的附加质量阵。郑治国和赵德有等[8]对利用结构有限元结合Green函数的边界积分法计算结构-流体的耦合作用,计算出非对称的附加质量矩阵,其利用的边界积分方程是基于源汇法而得出的。钱勤等[9]借助Green第二恒等式,将浸水结构的附加质量阵计算通过将速度势化为边界上的积分方程来计算,即边界积分公式。然后其用边界元数值方法将边界离散,从而计算出节点速度势,然后将速度势回带计算出附加质量阵。文献[10-13]同样利用源汇的思想,将流体运用布置在结构湿表面的源汇进行模拟,其优点是可以将流体从三维降至二维进行处理;但是由于其在源汇的布置方面以及物体表面源汇强度方面不连续等缺点,其在数值方法求解的时候比较繁琐,近年来使用这种方法解决附加质量阵问题相对较少。
将三维无限流体域降维转化为结构边界面上二维形式来处理,可以利用结构有限元耦合流体直接边界元的方法来求解附加质量阵,这种方法基本思想是将公式(4)或公式(5)在结构边界内做积分变换,将流体动压力Fa用(6)、(7)式或(8)式变换后的形式表示,进而求得附加质量矩阵Ma,其难点在于边界积分方程的推导和变换以及边界元所涉及的奇异积分处理问题。邹元杰和赵德有[14]针对水下结构声固耦合振动的特征值计算问题进行了研究,其水下结构附加质量阵的计算是基于直接边界元法推导的,而且指出假设镶嵌在无限大刚性障板上的结构,直接边界元理论的积分公式可进一步简化为Rayleigh积分来计算。付喜华和洪明等[15-17]对于可压缩流体和不可压缩流体的附加质量阵进行了研究,并利用无限大刚性障板的Rayleigh积分公式推导出了可压缩流体的动压力,进而推导出了其附加质量矩阵,同时给出了不可压缩流体的附加质量矩阵。施卫华[18]介绍了半无限流体域内声场的边界元解法,从半无限流体域边界积分方程出发,推导得到了板结构镶嵌在无限大刚性障板中时的Rayleigh积分方程,并求取了板式结构在水中的附加水质量。
魏建辉和陈美霞等[19]采用基于直接边界元基本理论的Helmholtz积分方程,利用单层圆柱壳在空气中的固有频率和固有振型,在模态坐标下推导出了结构附加质量的计算公式。安小同和洪明等[20]利用结构有限元原理和流体直接边界元原理对于浸水结构的附加质量阵进行了研究,给出了适用于低频作用下的基于直接边界元的附加质量阵的计算形式。文献[21-23]同样利用边界元理论对流体附加质量进行处理。综上可以看出Rayleigh积分公式可以用来处理假设镶嵌在无限大刚性障板上的结构(如局部加筋板),其优点是较直接边界元方法编程简单,其缺点是处理问题存在局限性;直接边界元方法其优点在于在理论上可以处理任意形状的与介质单面接触的封闭结构,但是其缺点在于对封闭结构的特征频率处解不唯一。无论是利用Rayleigh积分公式还是直接边界元方法处理浸水结构的附加质量阵Ma,其优点都在于将流体进行了降维处理,可以有效减少计算量。
对于可压缩流体和不可压缩流体的附加质量阵Ma,张升明[23]利用结构有限元和流体直接边界元方法,分别对流体为可压缩和不可压缩时,其对于结构振动特性的影响进行了研究。其指出:将流体视为可压缩时流体内各质点的运动相位是有差异的,运动相位差的存在说明了阻尼的存在,从而耗散能量;将流体视为不可压缩,流场内各质点运动是同相位的,因而它不产生阻尼。因此流体是否可压,就相当于是否考虑流体的阻尼。在低频时,流体压缩性对流体结构的振动固有频率影响很小,可以忽略。因此在低频时分析流体的附加质量,可以把流体作为不可压缩的介质;而无论低频或者高频,在研究分析结构在流体中的振动响应时,必须把流体作为可压缩的介质来处理。毛程亮和洪明等[24]针对浸水结构动力特性问题进行了计算,表明在低频范围内选取附加质量,流体的可压缩性对浸水结构的固有频率的影响非常小,在高频范围内随着计算频率的逐渐增加,流体的可压缩性对浸水结构的固有频率的影响将逐渐增大。
关于利用商业软件计算浸水结构的附加质量阵Ma,吴绍亮和金咸定[25]利用流体直接边界元理论得到流体的附加质量阵,对大型通用软件(MSC/NASTRAN)的流固耦合计算方法进行了应用开发。用MSC/PATRAN建立有限元模型,在MSC/NASTRAN平台上主要对流体直接边界元法、经验公式法进行结构的流体附加质量计算的对比研究和计算。这种方法的优点在于可以对大型复杂结构的附加质量进行求取,缺点在于有限元方法处理流体导致的单元以及节点增多,计算量增大。
3.1.2 浸水结构在流固耦合作用下的振动特性的研究
对于浸水结构在流固耦合作用下的振动特性的研究,普遍的研究是在解决附加质量阵Ma的基础上来进行的,研究人员普遍关心的问题是结构在流体中的振动模态。
无论是利用何种方法处理流体动压力Fa,对于浸水结构振动特性的研究其最终都需要对广义特征值方程(16)进行求解,模态叠加法是求解广义特征值方程的一种有效的方法。一般流固耦合系统的模态分析,根据计算过程的不同,可分为湿模态法和干模态法。
所谓干模态法是先求出结构在真空中较低的若干阶固有频率和固有模态(称为干模态),即先对运动方程(3)进行求解,得到干模态;然后将干模态进行模态坐标变换考虑流体的影响,利用求得的干模态结合耦合运动方程(16)进行求解,得到结构在流体中的固有频率和固有模态,其难点在于用何种方法如何求解方程(16)。汪庠宝等[2-3]给出了悬臂板和连续板的流固耦合振动的有限元计算格式的结构—流体系统耦合的无阻尼自由振动方程式,利用干模态法计算了悬臂版和连续板的流固耦合自由振动,给出了悬臂版在不同浸水深度下的固有频率。杨建民和汪庠宝[27]提出了一种计及流体与结构相互作用时船体结构模态计算的方法,船体结构用有限元法模拟,流体运动则用布置在船体表面的线性分布的三角形元源汇模拟。文中同时介绍了“湿模态法”以及“干模态法”计算流固耦合系统模态,并对两种方法进行了分析。徐张明和华宏星[42]利用FEM/I-BEM结合建立了结构—声耦合方程计算结构表面的振动特性,将结构的物理坐标用模态坐标来表示,对耦合的结构动力学方程及声场方程进行解耦。并分别对浸没于空气中和水中的椭圆球壳进行计算,其计算得出的结构表面振动速度表明,流体介质改变了结构的共振特性。文献[28-30]也利用了干模态的方法求解了浸水结构的固有振动特性,可见,干模态法较之湿模态法有一个明显的优点,即可分别利用现成的结构力学及流体力学领域中的最新研究成果来求解。同时,通过分析可知,较之湿模态法,干模态法中求解湿模态方程的自由度数目可大大缩小,即计算量大大减少;其缺点在于必须先求出结构的干模态,才能进一步求解结构的湿模态,过程较为繁复,且干模态阶数的选取在一定程度上影响求解精度。
所谓湿模态法是求解系统固有频率和固有模态时直接计及周围流体的动力影响对耦合运动方程(16)进行求解的方法。裴智勇和吴卫国等[4]将结构有限元法和流体有限元法结合起来,求得了高速船舱壁加筋板流固耦合系统的流体附加质量矩阵,利用湿模态法对高速船舱壁加筋板流固耦合系统进行了模态分析。郑治国和赵德有等[8]采用20节点三维等参元离散结构,在结构表现上布置源汇,应用Green函数的边界积分法计算流体—结构的相互影响,推导出系统的运动方程,用湿模态法对螺旋桨在水中的动力特性进行了计算。刘连海和洪明等[10,26]对流固耦合问题中结构采用有限元和流体采用边界元耦合的广义特征方程求解方法进行了研究,其指出由于流体附加质量矩阵的存在,由此耦合而成系统的总质量矩阵具有不对称性(这里针对的是直接边界元模型,对于间接边界元模型来说其是对称的)且是满阵,给特征值问题的求解带来了困难,其利用的双正交Lanczos法在一定程度上克服了上述困难。付喜华和洪明等[15-17]在求解流固耦合方程的特征值问题时,采用了迭代的Lanczos算法,即Lanczos算法与迭代算法结合的方法求解不对称频率相关特征值问题,安小同等[20]也利用这种方法对流固耦合方程的特征值问题进行了求解。文献[37-41,43-47]也利用了湿模态的方法求解了浸水结构的固有振动特性,湿模态方法较干模态方法优点在于其可以直接对浸水结构的固有模态进行求解,可以直观体现流体和结构的相互作用;其缺点在于计算量往往较干模态大。但近年来,由于数值计算水平的发展研究者一般偏重直接求取浸水结构的模态,即湿模态。
无论是利用干模态的方法还是湿模态的方法求解浸水结构的固有振动特性,终归是要对方程(16)进行求解,由有限元理论可知,方程(16)中质量阵M是对称矩阵,对称矩阵在计算机数值计算时是比较节省存储空间的,而附加质量矩阵Ma的对称性取决于所选用的对于流体的处理方法,文献[2-6]所利用的有限元处理流体的方法,其得到的附加质量矩阵Ma是非对称的;文献[19-23]所利用的直接边界元处理流体的方法,其得到的附加质量矩阵Ma同样是非对称的;文献[42,46]所利用的间接边界元处理流体的方法,其得到的附加质量矩阵Ma是对称的。可见利用间接边界元方法处理流体较直接边界元方法和有限元方法更能节省储存空间。所以,求解浸水结构的固有振动特性,其难点之一便是如何解决附加质量矩阵Ma的非对称性问题。
朱晓芳和金咸定等[31]利用有限元软件PATRAN/NASTRAN建立浸入水中圆柱体模型,并对其固有频率进行计算,分析比较了三种常用的浸水柱状结构固有频率的计算方法:干模态的经验修正系计算方法、流体力学两维理论计算方法和流固耦合数值计算方法。文献[32-36]同样论述了利用有限元软件PATRAN/NASTRAN或ANSYS来建立浸水结构模型,并对其固有频率进行数值计算,该方法已用于单
层和双层环肋增强圆柱壳的动力特性计算。此方法优点是可用于任意复杂浸水结构动力特性分析;缺点是计算节点多,计算量大。
3.1.3 相关实验研究
相对于数值模拟来说,国内对于实验验证数值模拟准确性的研究以及试验的研究相对较少。
裴智勇和吴卫国等[4]用湿模态法求得流体附加质量矩阵,依据结构有限元和流体有限元理论建立的加筋板结构流固耦合动力控制方程,编制了加筋板流固耦合振动计算程序。其为了认识高速船舱壁加筋板流固耦合动力性能,建立了船舶的局部模拟舱段结构,并进行模态试验,研究了舱内不同水深时舱壁加筋板结构流固耦合振动模态,同时与有限元计算结果进行了比较。
王杰德和杨永谦等[29]利用其对于船体薄壁梁弯扭动力分析的流固耦合数值计算结果与铝制船模在空气中和水中的实验得到的固有频率进行了对比,验证了其数值结果的可行性。谢志勇和周其斗等[41]采用钢质双层柱壳结构模拟潜艇结构,利用有限元软件建立数值分析模型并进行了相应的模态数值计算,之后分别对悬挂于空气中的柱壳:壳间充满空气的模态和壳间充水的模态两类情况进行了模态试验测量,并将试验结果与有限元法所得的计算结果进行了对比。
杨吉新和张可等[36]将用有限元软件ANSYS建模计算的悬臂柱在不同水位下的模态计算结果和实验进行了对比,实验结果与数值计算结果的差值小于10%,说明了这种数值方法是可行的。
童宗鹏和王国治[48]采用模态试验,利用单点激励多点响应的方式,对整个舰艇壳模型进行了测量,通过对舰艇结构传递函数的测量及试验数据的处理,得到了固有频率和振型,并与有限元的计算结果进行了对比。
胡选利等[49]对于声振耦合目前求解的三种常用方法:声弹性法、有限元法和边界元法进行了分析,对采用各种简化假设时三种方法的差异及统一进行了讨论。通过对矩形截面弹性薄壁箱体振动进行的实验测量,对各种理论模型所用简化假设的合理性进行了验证。
姚熊亮等[50]从实验和数值计算两个方面,对敷有隔声去耦材料的水下加筋圆柱壳体振动进行讨论分析。其实验地点选择在大型消音水池进行,在实验中测量了模型在水中的固有频率(湿模态),采用的方法是寻找响应曲线峰值点所对应的频率值,即共振频率。
对于浸水结构动力特性的实验研究相对较少,主要是由于其操作起来很复杂,如水下的实验器械选取以及布置安装等困难;而且其受到实验条件的影响极大,如用有限的水池模拟无限水域空间以及边界条件的选取等难题。但是,基于数值算法的验证、修正以及问题的发现和方法的改进,这类实验的开展还是十分有必要的。
3.2 浸水结构声辐射特性研究现状
3.2.1 弱耦合作用下的声辐射问题
对于结构在空气中(轻流体)的声辐射问题,一般视之为弱耦合,可忽略耦合作用。但是空气中结构声辐射问题的研究方法是研究浸水结构声辐射问题的基础,其对于流固耦合声辐射问题的研究,尤其是对于耦合方程中的质量阵,是非常具有借鉴意义的。
利用直接边界元方法来求解结构在轻流体中的声辐射问题是比较常用的方法,由于其不用考虑流固耦合的相互作用,可直接利用有限元方法对结构运动方程(2)求解得出结构在空气中的响应,将其作为求解声辐射问题的已知条件,利用边界积分公式(6)或(7)变换得到未知变量的方程组后,进而利用配点法等对结构声辐射特性进行求解。利用间接边界元方法来求解结构在轻流体中的声辐射问题是近年来研究的热点,若不用考虑流固耦合的相互作用,同样可直接利用有限元方法对结构运动方程(2)求解得出结构在空气中的响应,将其作为求解声辐射问题的已知条件,进而利用边界积分公式(10)进行变换计算,若声场满足Neumann边界条件则得到边界积分公式(11),利用公式(11)得到泛函方程(12),应用变分原理得到方程(13),进而求解结构声辐射特性。无论是直接或间接边界元方法其难点之一是对于各类奇异积分的处理。赵翔等[51]首先建立求解自由场中结构体声辐射的数学物理模型,从Helmholtz方程出发,用加权余量法推导Helmholtz方程的边界积分方程,即直接边界元的Helmholtz边界积分方程,然后用线性三角形单元离散边界,得到了边界积分的数值计算公式。编制了用于计算任意形状结构体声源的三维辐射声场的程序。对旋转式冰箱压缩机的辐射噪声场进行计算,并与实测结果进行了比较。黎胜等[52]采用结构有限元方法和流体边界元方法建立了轻流体介质中复杂结构振动声辐射的模态分析模型,文中以板和加筋板结构的振动声辐射为例进行了模态分析,并与用远场Rayleigh积分计算所得结果进行了比较。研究了激励力作用位置对板结构声辐射的影响和加筋板与板的模态辐射效率特点,并指出板加筋后会改变板的模态辐射效率规律。刘洪林[53]详细地推导出了对应于无限域和半无限域的振动声辐射问题的边界积分计算公式,并且比较了声辐射问题的直接边界元法和间接边界元法。利用直接边界元理论的积分公式处理结构在空气中的声辐射问题,其可以对任意形状的封闭结构进行场点声学特性的计算,其优点也在于此;缺点是其只能解决封闭结构问题,对于开口结构问题不能处理,而且其还存在特征频率解不唯一问题。文献[53]涉及到了间接边界元方法处理结构在空气中的声辐射问题,间接边界元方法优点在于可以处理任意形状封闭结构以及开口结构的声辐射问题;其缺点是推导较直接边界元法繁琐且数值处理复杂。
对于可以假定镶嵌在无限大障板上的结构,直接边界元的积分公式可以简化为Rayleigh积分公式(8),利用Rayleigh积分公式处理声辐射问题的难点同样是对奇异积分的处理。郭新毅和洪明[54-56]采用结构有限元和流体边界元(Rayleigh积分)相结合的方法对损伤结构振动及声辐射特性建立计算分析数值模型,得到结构的辐射声功率和辐射指向性,考虑到不同损伤存在形式,计算分析了损伤对振动频率、模态以及辐射声功率和指向性的影响。文献[57-61]同样利用Rayleigh积分公式来处理结构在空气中的声辐射问题,这种方法优点是其由直接边界元积分方程简化而来,积分公式相对简单,数值处理也相对简洁;其缺点在于其只能对于少部分可以假定镶嵌在无限大障板上的结构进行计算。
3.2.2 浸水结构的声辐射问题
对于结构在流固耦合下的声辐射,一般研究的是结构在重流体中的强耦合问题,是与浸水结构在流固耦合作用下的振动问题相辅相成的。无论是用那种方法处理结构和流体之间的相互关系,其最终都归结到对于结构表面的声压或声压差的求解,进而计算浸水结构声功率和声辐射效率等声辐射相关物理量。
对于浸水结构流固耦合作用下的声辐射问题,如果浸水结构的附加质量阵Ma是按照结构有限元耦合流体有限元的理论进行研究,其声辐射的求解可以直接利用有限元原理进行研究。不计阻尼影响,结构有限元耦合流体有限元模型(FEM/FEM)的系统运动方程如下:

其中:KS为结构模型的刚度矩阵;MS为结构模型的质量矩阵;KC为耦合刚度矩阵;KF为流体模型的刚度矩阵;MS为流体模型的质量矩阵;FSi为作用在结构上的激励力矢量;ui为节点位移;pi为节点动压力,即结构表面声压。由于这种方法在单元离散的过程中,随着计算频率的升高单元的密度将大大增加,因此科研人员往往利用另一种方式求解,即先求出浸水结构在流体中的振动响应,然后再利用所求出的振动响应结合边界元理论计算出浸水结构的声辐射特性。
如果浸水结构的附加质量阵Ma是按照结构有限元耦合流体边界元理论(直接或间接)进行研究,其声辐射特性一般是将流体动压力Fa表示成结构表面声压或声压差的函数,即将流体的动压力Fa用边界积分方程(6)、(7)、(8)或(10)的形式来表示,进而利用结构表面声压或声压差与结构表面法向振动速度的关系,以及法向振动速度与结构表面振速及位移的关系,对耦合方程(15)进行处理后联立Fa,求解联立方程组(18)或(19)得到浸水结构的声辐射特性。
不计阻尼影响,结构有限元耦合流体直接边界元模型(FEM/D-BEM)的系统运动方程如下:

其中:LC为耦合矩阵;T为法向速度和位移之间的转换矩阵;Aω()和Bω()为直接边界元影响矩阵。
不计阻尼影响,且满足单层势σ=0,则结构有限元耦合流体间接边界元模型(FEM/I-BEM)的系统运动方程如下:

其中:Qω()为间接边界元影响矩阵;ui为节点双层势(压力跳动量),即结构表面声压差。
对于可以假定镶嵌在无限大障板上的浸水结构,直接边界元的积分公式(6)或(7)可以简化为Rayleigh积分公式(8),将简化后的Rayleigh积分公式变换得到流体动压力Fa,将Fa代入耦合流体后的结构有限元运动方程(14)进而求出方程(15)联立Fa,并求解联立方程组(18)便可得到浸水结构的声辐射特性,其难点是有限元和Rayleigh积分方程的耦合以及奇异积分的处理。王其峰[12]利用Hess-Smith源汇方法对浸水结构的附加质量阵进行了推导,得出考虑流体加载效应的结构有限元方程并求解得出解决声辐射问题的边界条件。对于流固耦合作用下的声辐射问题,给出了一般问题的直接边界元法的Helmholtz积分方程以及镶嵌在无限大刚性障板上结构的Rayleigh积分方程,并概述了辐射声功率的多种计算方法。毛程亮[13]对流固耦合声辐射问题的研究方法及思路与王其峰类似,对半无限空间中的“软”“硬”边界进行了介绍。施卫华[19]利用Rayleigh积分方法对浸水结构的附加质量阵进行了推导,得出了考虑流体加载效应的结构有限元方程,并求解得出四边简支板的振动响应。对于流固耦合作用下的声辐射问题,其将四边简支板假设为镶嵌在无限大刚性障板上的结构,利用Rayleigh积分方程结合之前求解的振动响应得到了板在空气中和可压缩流体中的声辐射特性。文献[71-72,74,83-85]同样利用Rayleigh积分公式来处理浸水结构的声辐射问题,这种方法优点在于积分公式相对简单,数值处理也较直接边界元方法简洁,缺点在于其只能对于少部分可以假定镶嵌在无限大障板上的单面浸水结构进行计算。
对于单面浸水的封闭式结构,将直接边界元的积分公式(6)或(7)变换得到流体动压力Fa,将Fa代入耦合流体后的结构有限元运动方程(14)得到方程(15)并联立Fa求解联立方程组(18)便可得到浸水结构的声辐射特性,其难点在于非对称耦合矩阵以及奇异积分的处理。邹元杰和赵德有[43]利用结构有限元和流体直接边界元理论,建立耦合振动方程,并结合浅水域的声学边界条件,研究了水深对声辐射的影响。其对方箱结构声辐射进行数值计算后,得出的方箱结构在浅水中的声辐射功率等计算结果表明:浅水中的结构声辐射特性对水深有较强的依赖性。韩峰和闫桂荣等[45]利用LMS virtual lab中的Acoustic BEM模块实现了圆锥壳结构FEM/BEM声振耦合模型的仿真计算,基于结构声振耦合响应的计算求解结果,得到了所关心位置处的声压级,并将其与混响噪声实验测量结果进行比较,验证了结构声振耦合计算的正确性和合理性。沈顺根等[63]利用结构有限元耦合流体边界元,将结构有限元和修正的Helmholtz边界积分方程结合,建立了一种求解结构声辐射及物面动响应的矩阵分析方法。其对于流体的处理主要是利用直接边界元的基本原理来进行的。俞孟萨等[64]根据弹性结构振动和声辐射理论,采用结构有限元和流体边界元,系统地分析了水下运动体典型结构—有限长弹性加肋圆柱壳振动、耦合振动和声辐射的相似性,在公式推导的过程中强调了结构阻尼和流体负载的作用。崔宏武和赵德有等[73]对水下三维弹性结构振动的声辐射问题进行了流体—结构声耦合振动的数值计算。对结构部分采用有限元法(FEM),流体部分采用直接边界元法(D-BEM),推导并给出了基于流体直接边界元法和结构有限元方法协调的流体结构声耦合振动联立方程式,并讨论了其求解思路。文中着重研究了边界元法中矩阵元素的数值计算,编制了相应的计算机程序,利用脉动球算例验证了本文方法的正确性。文献[75-76,79-81]同样利用直接边界元理论的积分公式处理浸水结构的声辐射问题,其优点在于其可以解决任意形状单面浸水封闭结构的声辐射问题;其缺点在于求解运动方程(15)和Fa联立方程组的时候无论是对于非对称矩阵的存储还是对非对称矩阵方程的求解都存在较大的困难,而且其不能处理开口结构问题。
对于双面浸水的封闭式结构或开口结构,将间接边界元的积分公式(10)变换得到流体动压力Fa,将Fa代入耦合流体后的结构有限元运动方程(14)得到方程(15)联立Fa,并求解联立方程组(19)便可得到双面浸水浸水结构的声辐射特性。其难点在于有限元和间接边界积分方程的耦合以及超奇异积分或超奇异积分转化后的双层弱奇异积分的处理。徐张明和华宏星等[42]将有限元和间接边界元结合得到声振耦合方程,进而计算相应的辐射声场。其对一水下受均布谐载荷的球壳进行数值计算来验证其方法的正确性,分别得到了球壳在空气中和水中的辐射声压、辐射声功率和辐射效率。这种方法的最大优点是可以同时计算结构表面振动和辐射声场,而且适用于任意复杂结构。魏建辉和陈美霞等[46]基于结构有限元和流体间接边界元方法(FEM/I-BEM)研究了双层圆柱壳的振动及声辐射,并与解析法及目前常用的数值算法:结构有限元耦合结构有限元,结构有限元耦合直接边界元方法进行了对比,验证了本方法的正确性。指出了结构有限元和流体间接边界元计算方法可以很好地用于解决水下双层圆柱壳的振动及声辐射问题。利用间接边界元方法处理浸水结构的声辐射问题,其优点在于可以处理任意形状双面浸水的封闭结构以及开口结构的声辐射问题,而且其得到的耦合矩阵是对称阵,对于矩阵的存储可以节省内存空间,并且对称矩阵方程的求解较非对称矩阵方程容易求解;其缺点是推导过程繁琐复杂,较直接边界元在奇异积分等数值处理上更为困难。综上可见,无论是Rayleigh积分公式、直接边界元法还是间接边界元法,其都可以有效地结合有限元方法,将结构模拟为有限元处理,将流体降维利用边界元来处理,进而直接求解流固耦合运动方程。
姚熊亮等[32,50]对双壳体结构的声辐射特性进行了研究,其主要是将有限元软件ANSYS建模并计算的浸水双壳体的振动响应带入到了声学软件SYSNOISE利用其直接边界元计算模块来计算浸水双壳体的振动特性。文献[33-35,38,40,62,65-70,77-78,82]同样论述了利用有限元软件ANSYS结合SYSNOISE来建立浸水结构模型,对其声辐射特性进行数值计算,该方法已用于单层、双层环肋增强圆柱壳等浸水结构的声辐射特性计算,此方法优点是可用于任意复杂浸水结构的声辐射特性分析;缺点是其有限元和边界元的计算是分开进行的,其存在将有限元的计算结果导入边界元程序的复杂过程,而且其将流体截断为有限元进行处理,若要得到较精确结果其计算单元和节点会较多进而计算量会较大。
3.2.3 关于直/间接边界元方法解的非唯一性问题
声辐射问题一般采用Helmholtz微分方程在边界条件下形成的定解方程来描述,其解具有唯一性,但是一旦采用Helmholtz边界积分方程对上述定解方程进行求解,在某些波数(以结构封闭表面为界的内部Dirichlet问题的特征频率)处就会出现非唯一性的现象,产生非唯一性的原因是由于在这些波数处,解的边界积分表述与原问题之间不存在对等性。
对于特征频率处解的非唯一性问题,有两种最具有代表性的方法,一种1968年Schenck年提出的CHIEF方法(Combined Helmholtz Integral Equation Formulation),另一种是1971年Burton与Miller提出的Burton-Miller法。众多其它的方法都是在这两种方法的基础上对其进行改进而进行的。施卫华[19]对于无限域自由场中的三维封闭弹性体结构,采用直接边界元法计算结构的声辐射。利用CHIEF法解决特征频率处解不唯一的问题。文献[67,69]同样采用了CHIEF法解决Helmholtz积分方程解的非唯一性问题。文献[89-92]同样利用CHIEF方法处理特征频率处解不唯一的问题,其优点在于,不在非常高的激励频率下,CHIEF点的选取并不困难,只要有一个CHIEF点有效,CHIEF方法就有效;其缺点在于,在高频情形下,由于此时振型十分密集,节点的密度大大增加,CHIEF点的选取在振型节点上的概率也大大增加,选取合适的CHIEF点也更加困难。文献[86-88]所使用的内部Helmholtz方程关于内点坐标取导后构成补充方程式方法与CHIEF方法相比较,能更有效地处理特征频率处解不唯一的问题。
蒋伟和何正耀等[93]应用了一种无界声媒质空间中任意形状辐射体辐射声场的新方法—综合H-elmholtz积分公式法(Synthetic Helmholtz Integral Equation Formulation,SHIEF)。其推导是基于直接边界元理论的,主要解决了当辐射体的振动频率等于或接近其特征频率时,声辐射出现奇异解的问题。该方法将关于辐射体的内部、表面和外部Helmholtz积分方程有机地组合在一起,在已知辐射体表面法向振速的条件下,求出辐射体表面的声压分布,进而求得其辐射声场分布。该方法将外部、表面以及内部Helmholtz积分方程有机地结合起来,减少了对辐射体内部点的依赖,并且充分利用内外辐射声场的信息,克服了CHIEF法内部点选取的困难和超定外部Helmholtz积分公式法在特征频率处和高频段收敛速度慢以及所需外点数多的缺点。
3.2.4 关于直/间接边界元奇异积分的处理
不论是直接边界元理论的Helmholtz积分方程还是间接边界元理论的Helmholtz积分方程,亦或是直接边界元理论的Helmholtz积分方程的特殊形式Rayleigh积分方程,都存在奇异积分的问题,对于奇异积分的处理是解决Helmholtz积分方程或Rayleigh积分方程的重中之重也是难点所在。奇异积分根据边界归化的途径不同,可能有三种类型:弱奇异O);Cauchy型奇异O);超奇异。超奇异积分又称为Hadamard型奇异积分,其具有比Cauchy型奇异积分更高阶的奇异性,根据经典微积分学的概念,Hadamard型奇异积分是发散且没有意义的,无法用经典的数值积分公式计算出其具有一定精度的近似值,它们只有在Cauchy主值意义下才存在,边界元法中的Hadamard型奇异积分实际上是其有限部分。
对于弱奇异积分的研究,刘连海[10]对于Rayleigh积分中弱奇异积分的处理利用的是退化单元的方法。对于四边形单元,其将四边形单元分解为若干三角形单元,对含奇异点的三角形单元进行适当的坐标变换以消除奇异性。柯兵和谭林森等[61]对于直接边界元法存在的奇异性问题,借助于引进退化单元,将三角形单元再分成三个三角形单元进行处理,解决了基本解的弱奇异性问题。杨勇[69]在处理基于表面的Rayleigh积分方程的弱奇异积分时,对于4节点线性单元,其引入了退化元消除了单元上的积分奇异性。黎胜等[90]对于直接边界元Helmholtz积分方程的积分奇异性处理,采用三角形斜坐标系、退化单元方法。对于线性三角形单元采用三角形斜坐标系来消除积分奇异性;对于四边形线性元和四边形二次元采用退化元来消除积分奇异性。李宏伟和文立华等[100]提出了采用三角形或四边形改进的二次插值函数,并结合局部极坐标变换或引入退化单元的方法,解决了任意三维非光滑结构表面声学计算边界元法中的奇异积分问题。其采用的三角形单元为六节点三角形单元,四边形单元为八节点四边形单元,但是其插值函数并非一般常见的二次插值函数,而是改进的二次差值函数。其所说的退化单元,是将三角形或四边形单元分为两个子单元来进行奇异积分的计算。利用退化单元的方法来解决奇异积分问题,其优点是对于处理弱奇异积分是非常有效的;缺点是其不能对高阶奇异积分进行处理,且对于单元的形状也有一定要求。
刘洪林[53]指出对于弱奇异积分的数值计算,目前最有效的处理方法是极坐标变换法;对于强奇异积分,可以首先将其变换为主值积分和奇点自由项的组合,然后通过适当的数学变换(如配项处理、坐标变换等)将其降奇后再进行求解,而且由于这种强奇性积分显然都位于系数矩阵的对角线上,因而利用物理学中的均匀场的概念,可以间接地对强奇性积分进行求解。李小明[67]是基于直接边界元理论的Helmholtz积分方程来求解声辐射问题,其采用极坐标法消除四边形线性元中的弱奇异积分。赵键和汪鸿振等[86]在解决直接边界元的Helmholtz积分方程的奇异积分方面,提出了在奇异点附近的积分区域,利用极坐标变换消除积分的奇异性,将奇异积分变为被积函数无奇异点的普通积分来处理,并给出了表面Helmholtz方程、CHIEF及该文方法处理与不处理奇异积分的比较结果,得出经该文介绍的办法处理奇异积分后,各方法的计算误差减小了一个数量级。利用极坐标变化的方法来解决奇异积分问题,这种方法较退化单元法在处理弱奇异积分在积分变换方面更有效,但是其缺点同样是不能处理高阶奇异积分问题。
程昊等[58]对于直接边界元法所涉及的奇异积分处理,采用替换点法,其基本思路是在奇异点周围,不连续常单元内选择适当的几个点,分别将这些点看作新的源点,通过采用高斯积分方法计算这些新源点与原奇异点,即场点之间的系数值,用这些选定的奇异点周围的点代替奇异点计算积分值,然后将所有替换点所求得的值取平均值用以代替原奇异点处的值。这种方法在处理弱奇异积分时,可以在一定程度上减少计算量。
对于Cauchy奇异积分的处理,朱春浩和谭林森[95]对于直接边界元法应用于计算流固耦合问题时的弱奇异积分以及Cauchy奇异积分问题进行讨论,尤其是对于二次奇异积分问题的处理进行了详细的推导和证明,并以八节点曲边单元为例讨论了二次奇异积分的处理方式。孙亮和滕斌等[97]对于弱奇异积分进行了研究,对源点附近的单元即存在弱奇异积分的单元进行细分,从而改变计算区域上高斯积分点的分布。就是说在弱奇异积分点附近进行积分点加密,对于远离弱奇异积分点的积分使积分点分布稀疏一些。张秀珍[98]对于弹性问题的三维边界积分方程中的弱奇异积分和Cauchy奇异积分进行了讨论,提出利用线性位移函数消除弱奇异因子;用刚体位移原理消除Cauchy奇异因子,避免了强奇异因子向弱奇异因子转化计算效率低的问题。赵志高和黄其柏[99]提出了一种非等参单元的四边形坐标变换,其将积分的曲面单元映射为另一四边形单元,通过两次坐标变换引入的雅可比行列式可以消除Helmholtz声学边界积分方程中的弱奇异型积分,利用∂R/∂n以及坐标变换可以同时消除坐标变换无法消除的Cauchy型奇异积分。李小瑜和傅志方[101]对边界积分方程和边界元技术计算结构的稳态外辐射声场的方法进行了研究,对边界元方法所固有的奇异数值积分给出了处理方法,对于弱奇异积分其通过线性变换来进行处理,对于Cauchy奇异积分的处理则是给出了利用离散后得到的线性方程组的特点来进行处理。
对于超奇异积分的处理,闫再友等[89,96]在利用复合Helmholtz积分方程时,由于引入了表面Helmholtz积分方程的法向导数方程,所以导致了其积分算子中存在超奇异积分,其利用正则化关系式将超奇异积分算子降为弱奇异积分,然后对弱奇异积分进行处理,从而解决超奇异积分计算的困难。其优点在于可以直接快速地求出超奇异积分算子所对应的系数矩阵。董春迎和姚振汉等[94]对边界积分方程中存在的超奇异积分的数值解法作了介绍,其分别介绍了分部积分法、Stokes理论、散度理论、Guiggiani法和Kutt法等9种处理超奇异积分方法,文中虽然只针对于弹性问题的奇异积分方程的奇异积分进行具体描述,但是对间接边界元的Helmholtz积分方程的超强奇异积分处理是可以借鉴的。
在一般情况下,利用间接边界元方法解Helmholtz积分方程,其超奇异积分的处理都是转化成为双层弱奇异积分来进行的,只是这种双层弱奇异积分的处理较直接边界元涉及到的弱奇异积分的处理更为困难,而且这种奇异积分问题处理是否得当是决定间接边界元方法计算是否准确的核心因素之一,国内对于这类问题的研究非常少。
3.3 浸水结构振动及声辐射特性工程问题的一些处理方法
对于浸水结构在流固耦合作用下振动及声辐射特性的实际工程问题来说,其研究的结构往往是复杂的而且相对尺寸是非常庞大的,现阶段研究人员一般较为常用的处理方法是直接利用有限元商业软件进行结构和流体的建模,基于圣维南原理将无限域流体简化为有限域流体,利用其内部的求解器进行浸水结构振动特性的求解。
童宗鹏和王国治[48]以舰艇结构振动与噪声预报为研究背景,采用有限元方法利用有限元软件ANSYS对舰艇的干模型进行研究,通过有限元模态计算和模态试验对理论计算模型进行修正,确定舰艇干模型的参数;在该工作的基础上,建立舰艇的流固耦合模型,模拟激振力施加在发动机上,进行流固耦合计算,得到舰艇外层壳体表面节点的位移。徐张明和华宏星等[102]利用有限元软件ANSYS计算船舶结构与水下声场的耦合振动,其在研究的过程中利用ANSYS软件建立了水下船舶振动的有限元模型,并计算了模型的湿模态以及在动力系统中模拟的激励源作用下的船舶壳板振动响应,其船体结构和流体都是利用有限元单元来进行模拟的。基于对浸水结构振动特性的计算,将计算得到的外壳面上的振动速度作为声场计算的边界条件,利用边界元软件SYSNOISE计算声学物理量。该文的方法为解决大型复杂结构的耦合声振预报提供了一个典型的实例。文献[103-105]同样利用有限元软件ANSYS等结合边界元软件SYSNOISE等计算实际工程浸水结构流固耦合振动及声辐射特性问题,这种方法需要分别对流体和结构进行有限元的单元划分,该方法已用水下工程结构物以及水面舰艇的动力特性计算,此方法优点是可用于任意复杂实际工程浸水结构振动及声辐射特性分析;缺点是由于其流体区域的有限元划分存在截断误差,若需要得到较为精确的计算结果,往往单元划分得会比较多且比较精细,进而计算量会非常大。而且在计算声辐射特性时需要将有限元的计算结果导入边界元软件中,操作较繁琐。
4 结语
对国内相关文献进行分类总结后,关于浸水结构振动及声辐射特性研究现状有如下观点:
(1)基于FEM/FEM的浸水结构流固耦合振动特性的研究,相对于其他研究方法在一些领域较为成熟,但是其缺点也比较明显,即对于无限流体域的截断误差和对于三维流体域的计算量较大等;
(2)基于FEM/D-BEM的浸水结构流固耦合振动特性的研究发展相对较FEM/I-BEM在某些领域的研究发展要成熟一些,但其本身仍存在一些局限。如基于直接边界元理论推导得出的附加质量矩阵是非对称的满阵,在求解广义特征方程的过程中存在一定的困难;不适用于开口结构的研究等;
(3)基于FEM/I-BEM的浸水结构流固耦合振动特性的研究,优点是基于间接边界元推导得出的附加质量阵是对称的满阵,在解决广义特征方程的过程中比D-BEM更有优势,适用于开口结构的研究等。但是由于其存在超奇异积分等特点,同样给问题的解决带来很大困难;
(4)对于实际工程中重流体中低频振动结构附加质量的计算,尤其是船舶的附加质量的公式估算,本文虽没过多涉及,但其无疑是科研和工程设计人员感兴趣的。Korotkin[106]对船舶及相关构件附加质量系统地给出了适合工程实际的简便算法,包括各种船舶结构在多种条件下(如固壁附近和自由表面附近等)的附加质量计算公式,为设计提供了简单实用方法;
(5)对于浸水结构的声辐射问题,利用FEM/D-BEM方法,无论是在解决其特征频率处解的非唯一性问题还是非超奇异积分的问题已经有一些相对有效的处理办法;但对I-BEM在解决某些问题时其积分方程涉及到超奇异积分问题,解决的方法相对于直接边界元解决非超奇异积分的方法还是少一些;
(6)无论是实验验证还是试验研究,对于结构流固耦合振动特性问题都相对较少;对于结构在流固耦合作用下的声辐射方面的实验验证及试验研究,由于其操作起来更加困难,所以这方面的工作要更少一些。故对于这两方面的研究还有待深入发展;
(7)虽然对结构声辐射灵敏度问题目前有些研究[58-60],但是对于浸水结构声辐射灵敏度问题还是鲜有研究;
(8)对于本文所涉及的相关流固耦合振动及声辐射特性问题的文章,按照处理结构和流体耦合时的三种不同的方法:FEM/FEM、FEM/D-BEM和FEM/I-BEM进行分类。从图5可以看出对于FEM/IBEM的研究相对较少;
(9)对于本文所涉及的相关流固耦合振动及声辐射特性问题的文章,按照处理声辐射问题的两种不同的方法:D-BEM和I-BEM进行分类。从图6可以看出对于I-BEM的研究相对较少;
(10)对于本文所涉及的相关流固耦合振动及声辐射特性问题的文章,按照数值模拟方法的两种不同途径分类,图7表明文章基于计算机编程研究要多于基于商业软件计算;
(11)对于本文所涉及的相关流固耦合振动及声辐射特性问题的文章,覆盖的年代范围是1985年到2011年,其年份分布如图8所示。
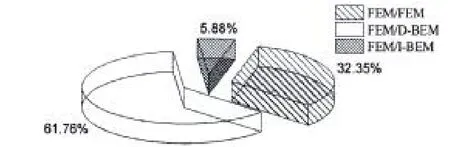
图5 文章分类:按照处理结构和流体耦合问题时的三种方法Fig.5 Paper categories:According to the threemethods of processing fluid and structure coupling problem

图6 文章分类:按照处理声辐射问题的两种方法Fig.6 Paper categories:According to the twomethods of processing acoustic radiation problem
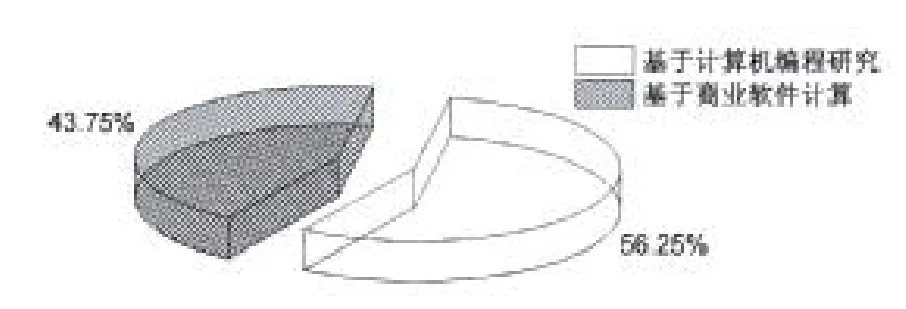
图7 文章分类:按照数值模拟方法的两种不同途径Fig.7 Paper categories:According to the two ways of numerical simulationmethod
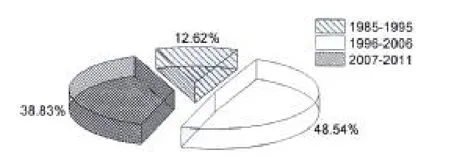
图8 文章分类:按年份分布Fig.8 Paper categories:According to the chronology
[1]Atalla N.Review of numerical solutions for low-frequency structural-acoustic problems[J].Applied Acoustics,1994,43 (3):271-294.
[2]汪庠宝,韩继文,陆鑫森.悬臂板和连续板的流固耦合振动解[J].中国造船,1988(2):53-63.
[3]汪庠宝,韩继文,陆鑫森.船底板流固耦合振动的有限元解[J].振动与冲击,1985(4):8-15.
[4]裴智勇,吴卫国,翁长俭.高速船舱壁加筋板流固耦合振动分析[J].工程力学,2003(2):159-162.
[5]童予靖,刘正兴.流固耦合问题中的附连水质量研究[J].上海力学,1997(4):311-320.
[6]金占礼,王宗利等.结构在无限流体域中振动时附连水质量的数值计算方法[J].上海交通大学学报,2000(8):1078-10820.
[7]王国强,杨建民.用线性三角形元源汇法计算振动船体的附连水质量[J].上海交通大学学报,1988(3):99-103.
[8]郑治国,王镐章,赵德有.螺旋桨的流固耦合动力分析[J].大连理工大学学报,1996(2):219-223.
[9]钱勤,黄玉盈,刘忠族.求附连水质量的一种直接方法[J].力学与实践,1996(5):20-22.
[10]刘连海.含损伤加筋结构水中振动与声辐射特性研究[D].大连:大连理工大学,2006.
[11]刘连海,洪明,郭新毅.含损伤加筋结构流固耦合动力特性与声辐射特性研究[J].中国舰船研究,2007(2):9-14.
[12]王其峰.流体加载下含损伤板式结构声振特性研究[D].大连:大连理工大学,2009.
13]毛程亮.船舶板式结构振动及声辐射特性研究[D].大连:大连理工大学,2009.
[14]邹元杰,赵德有.水下结构声固耦合振动的特征值计算[J].船舶力学,2004,8(2):109-120.
[15]付喜华,洪明,刘连海.舰船加筋结构声辐射数值模拟方法研究[Z].中国陕西西安:2007:28-34.
[16]付喜华.舰船加筋结构声辐射阻尼研究[D].大连:大连理工大学,2008.
[17]付喜华,洪明,郭新毅.流体中弹性板声辐射阻尼研究[J].中国舰船研究,2008(1):42-47.
[18]施卫华.浸水结构动力特性与声辐射特性研究[D].大连:大连理工大学,2010.
[19]魏建辉,陈美霞,和卫平等.基于空气中模态参数的水中结构固有频率估算方法研究[C]//第十二届船舶水下噪声学术讨论会论文集.中国长沙,2009:115-121.
[20]安小同,洪明,李艮田.基于BEM/FEM计算浸水结构振动特性[J].船海工程,2011(6):55-58.
[21]苏海东,黄玉盈.求半无限域流场中物体附连水质量的一种简便解法[J].华中科技大学学报(城市科学版),2003(4): 14-16.
[22]李华东,朱锡,罗忠等.附连水质量的边界元法求解[J].海军工程大学学报,2009(2):45-49.
[23]张升明.流体的可压缩性对弹性结构振动的影响[J].水动力学研究与进展(A辑),1994(4):429-436.
[24]毛程亮,洪明.流体可压缩性对板及加筋板声振特性数值模拟的影响[C]//第四届全国船舶与海洋工程学术会议论文集.中国镇江,2009:23-28.
[25]吴绍亮,金咸定.流固耦合计算方法在船舶局部结构中的应用[J].振动与冲击,2003(4):28-30.
[26]刘连海,洪明等.结构流固耦合动力分析中非对称广义特征值问题Lanczos算法[C]//2006中国大连国际海事论坛论文集.中国大连,2006.
[27]杨建民,汪庠宝,王国强.船体结构流固耦合模态分析[J].上海交通大学学报,1993(1):19-26.
[28]吴芳.板和加筋板附加水质量算法研究[D].大连:大连理工大学,2006.
[29]王杰德,杨永谦,毛政良.船体薄壁梁弯扭动力分析的流固耦合边界元法[J].武汉交通科技大学学报,1995(4):345-352.
[30]沈惠明,赵德有,罗志雍.流固耦合振动问题的特征值解法[J].大连理工大学学报,1990(3):369-371.
[31]朱晓芳,杜志鹏,金咸定.浸入水中的船舶尾轴架固有频率的计算方法探讨[J].振动与冲击,2005(2):111-115.
[32]姚熊亮,杨娜娜,陶景桥.双层壳体水下振动和声辐射的仿真分析[J].哈尔滨工程大学学报,2004(2):136-140.
[33]陈乐佳,骆东平,关珊珊等.潜艇双层壳体振动特性与声辐射性能FEM/BEM分析[C]//第十届船舶水下噪声学术讨论会论文集.中国烟台,2005:104-110.
[34]高菊,陈美霞,段晔鑫.基于FEM/BEM的环肋圆柱壳振动及声辐射相似性数值分析[C]//第十二届船舶水下噪声学术讨论会论文集.中国长沙,2009:44-51.
[35]尹绪超,姚熊亮,金叶青.轴向激励下加肋圆柱壳体振动及声辐射特性研究[C]//第十三届船舶水下噪声学术讨论会论文集.中国鹰潭,2011:166-171.
[36]杨吉新,张可,党慧慧.基于ANSYS的流固耦合动力分析方法[J].船海工程,2008(6):86-89.
[37]朱克强,李道根,姚震球等.海洋浮式结构流固耦合动力建模分析[J].华东船舶工业学院学报(自然科学版),2002(1): 1-6.
[38]孙玉东,俞孟萨,李东升等.带液舱水面船舶振动和声辐射的计算与分析[C]//第十届船舶水下噪声学术讨论会论文集.中国烟台,2005:111-116.
[39]孙士丽,王诗平,姚熊亮等.板和加筋板流固耦合振动特性研究[C]//黑龙江省造船工程学会2008年学术年会论文集.中国哈尔滨,2008:142-146.
[40]陈美霞,杜磊,陈乐佳等.基于边界元法的平板结构声振性能数值计算[J].武汉理工大学学报,2009(6):1048-1051.
[41]谢志勇,周其斗,纪刚.双层柱壳的流固耦合模态计算与试验研究[J].海军工程大学学报,2009(2):97-101.
[42]徐张明,沈荣瀛,华宏星.利用FEM/IBEM计算流体介质中的壳体的结构声耦合问题[J].振动工程学报,2002(3): 119-123.
[43]邹元杰,赵德有.结构在浅水中的振动和声辐射特性研究[J].振动工程学报,2004(3):21-26.
[44]岳鹏,黎胜,赵德有.船体薄壁梁弯扭耦合振动的流固耦合分析[J].船舶力学,2009(2):290-297.
[45]韩峰,胡迪科,闫桂荣.圆锥壳结构声振耦合特性分析[J].噪声与振动控制,2009(5):30-33.
[46]魏建辉,陈美霞,牟彬杰等.基于IBEM的水下双层圆柱壳声振性能研究[J].舰船科学技术,2011(7):9-13.
[47]白长青,周进雄,闫桂荣.声振耦合对薄壁圆柱结构动力特性的影响[J].机械工程学报,2011(5):78-84.
[48]童宗鹏,王国治.舰艇结构水下振动和声辐射特性研究[J].华东船舶工业学院学报(自然科学版),2003(2):18-22.
[49]胡选利,陈花玲,赵建平.声振耦合数值模型合理性分析和实验验证[J].西安交通大学学报,1997(7):3-8.
[50]姚熊亮,刘庆杰,翁强等.水下加筋圆柱壳体的振动与近场声辐射研究[J].中国舰船研究,2006(2):13-19.
[51]赵翔,黄幼玲,谢壮宁.自由场结构体声辐射研究[J].声学学报,1994(1):22-31.
[52]黎胜,赵德有.用有限元/边界元方法进行结构声辐射的模态分析[J].声学学报,2001(2):174-179.
[53]刘洪林.船舶结构振动与声辐射分析[D].上海:上海交通大学,2003.
[54]郭新毅,洪明,李艮田.含损伤加筋板结构辐射声功率及指向性变异研究[J].船舶力学,2005,9(4):119-129.
[55]郭新毅,洪明,李艮田.含损伤加筋板结构声辐射模态变异研究[J].船舶力学,2005,9(2):115-123.
[56]郭新毅.含损伤加筋板结构振动与声特性变异研究[D].大连:大连理工大学,2005.
[57]赵志高,黄其柏,何锃.基于有限元边界元方法的薄板声辐射分析[J].噪声与振动控制,2008(1):39-43.
[58]程昊,高煜,张永斌等.振动体声学灵敏度分析的边界元法[J].机械工程学报,2008(7):45-51.
[59]陈剑,程昊,高煜等.基于有限元-边界元的声学构形灵敏度分析[J].振动工程学报,2009(2):213-217.
[60]张波,沈火明,支伟.有限元/边界元法求解变厚度板的声辐射[J].科学技术与工程,2010(36):8963-8967.
[61]柯兵,谭林森.用有限元/边界元方法计算结构体振动辐射声场[J].船海工程,2001(S2):97-99.
[62]陈美霞,邱昌林,骆东平.基于FEM/BEM法的内部声激励水下圆柱壳声辐射计算[J].中国舰船研究,2007(6):50-54.
[63]沈顺根,李琪华,王大云等.加肋旋转壳结构噪声声辐射水弹性研究[J].中国造船,1992(2):55-64.
[64]俞孟萨,史小军,陈克勤.采用有限元和边界元方法分析弹性加肋圆柱壳的声学相似性[J].中国造船,1999(3):65-71.
[65]张阿漫,钱德进,姚熊亮.结构型式对双层壳声辐射特性影响研究[J].中国舰船研究,2007(3):1-6.
[66]石焕文,盛美萍,孙进才等.加纵肋平底圆柱壳振动和声辐射的FEM/BEM研究[J].振动与冲击,2006(2):88-92.
[67]李小明.加肋圆柱壳振动声辐射特性的数值计算研究[D].大连:大连理工大学,2008.
[68]袁自强.圆柱壳的振动声辐射的数值分析[D].武汉:华中科技大学,2008.
[69]杨勇.周期加强薄板声辐射数值方法研究[D].大连:大连理工大学,2009.
[70]金叶青,姚熊亮,尹绪超等.复杂锥柱结构声辐射数值计算研究[C]//第十三届船舶水下噪声学术讨论会论文集.中国鹰潭,2011:127-133.
[71]洪明,郭新毅,刘连海.含损伤加筋结构的振动与声辐射特性研究[J].中国舰船研究,2007(6):35-41.
[72]张升明,潘旭初.板架结构的振动噪声研究[J].噪声与振动控制,1995(5):9-13.
[73]崔宏武,赵德有,罗志雍等.结构振动的水中声辐射计算[J].中国造船,1990(4):51-56.
[74]黎胜,赵德有.流体加载下加肋板结构的声辐射特性研究[J].应用声学,2000(6):28-32.
[75]黎胜,赵德有.用耦合有限元/边界元方法研究加筋板的声传输[J].振动工程学报,2001(3):120-123.
[76]黎胜,赵德有.水下结构振动和声辐射的模态分析及控制研究[C]//水下噪声学术论文选集(1985-2005).中国烟台,2005:45-56.
[77]杨德庆,郑靖明,王德禹等.基于SYSNOISE软件的船舶振动声学数值计算[J].中国造船,2002(4):32-37.
[78]杨德庆,王德禹,刘洪林.舰艇振动声学特性数值分析[J].上海交通大学学报,2002(11):1537-1539.
[79]郝承智.水下加肋壳体振动与声辐射特性研究[D].西北工业大学,2006.
[80]洪明,王其峰,刘连海等.轻/重流体介质中振动板声辐射模态下的声辐射阻尼研究[J].船舶力学,2009,13(5): 813-821.
[81]郭新毅,洪明.结构振动声辐射阻尼研究[C]//2004年船舶与海洋工程学术研讨会论文集.2004:189-196.
[82]程武山.ANSYS软件与SYSNOISE软件结合的声辐射分析[C]//全国先进制造技术高层论坛暨第九届制造业自动化与信息化技术研讨会论文集.中国武夷山,2010:299-302.
[83]杨婧媛.水下结构声辐射的响应变异性分析及代理模型研究[D].大连:大连理工大学,2010.
[84]施卫华,邓海华,陈明.浸水板式结构的动力特性与声辐射特性数值分析[J].舰船科学技术,2011(8):29-37.
[85]安小同.基于有限元/边界元的水下结构振动声辐射研究[D].大连:大连理工大学,2011.
[86]赵键,汪鸿振,朱物华.边界元法计算已知振速封闭面的声辐射[J].声学学报,1989(4):250-257.
[87]赵键,汪鸿振,朱物华.改进计算对称壳体声辐射的边界积分方程法[J].上海交通大学学报,1989(4):61-69.
[88]赵键,汪鸿振.用边界积分方程法计算封闭体的声辐射[C]//水下噪声学术论文选集(1985-2005).中国烟台,2005: 4-17.
[89]闫再友,姜楫,严明.利用边界元法计算无界声场中结构体声辐射[J].上海交通大学学报,2000(4):520-523.
[90]黎胜,赵德有.用边界元法计算结构振动辐射声场[J].大连理工大学学报,2000(4):391-394.
[91]白杨,汪鸿振.声学-结构设计灵敏度分析[J].振动与冲击,2003(3):45-47.
[92]赵志高,黄其柏.复杂结构的声辐射解耦及其声辐射效率分析[J].振动工程学报,2004(3):78-83.
[93]蒋伟,何正耀,王冬海.辐射体声场计算的综合Helmholtz积分公式法[J].电声技术,2006(10):9-12.
[94]董春迎,杜庆华,谢志成,姚振汉.边界积分方程中超奇异积分的解法[J].力学进展,1995(3):424-429.
[95]朱春浩等.用边界元法计算流固耦合问题时高次奇异积分的处理方法[J].武汉船舶职业技术学院学报,2002(4):49-52.
[96]闫再友,姜楫,何友声等.声学边界元方法中超奇异数值积分处理的新方法[J].声学学报,2001(3):282-286.
[97]孙亮,滕斌,宁德志.处理准奇异积分的自适应高斯积分法[J].大连理工大学学报,2007(1):106-112.
[98]张秀珍.三维边界积分方程中的奇异积分的处理[J].装甲兵工程学院学报,2003(3):17-19.
[99]赵志高,黄其柏.Helmholtz声学边界积分方程中奇异积分的计算[J].工程数学学报,2004(5):779-784.
[100]李宏伟,文立华,陈克安.非光滑结构表面声学边界元法中奇异积分计算方法[J].西北工业大学学报,2006(4): 497-500.
[101]李小瑜,傅志方.结构振动辐射声场的预估-边界积分方程中奇异积分的间接处理[J].振动工程学报,1989(1):59-65.
[102]徐张明,汪玉,华宏星等.船舶结构的建模及水下振动和辐射噪声的FEM/BEM计算[J].船舶力学,2002,6(4): 89-95.
[103]徐张明,汪玉,华宏星等.双层壳体的船舶动力舱振动与声辐射的有限元结合边界元数值计算[J].中国造船, 2002(4):39-44.
[104]彭旭,骆东平.船舶结构建模及水下振动和辐射噪声预报[J].噪声与振动控制,2003(6):9-12.
[105]邹春平,陈端石,华宏星.船舶水下辐射噪声特性研究[J].船舶力学,2004,8(1):113-124.
[106]Korotkin A I.Added Masses of Ship Structures[M].Springer,2007.
Domestic review of the submerged structure vibration and acoustic radiation characteristics based on FEM/BEM
WANG Zhenga,HONGMinga,b,LIU Chenga
(a.School of Naval Architecture Engineering;b.State Key Laboratory of Structure Analysis for Industrial Equipment, Dalian University of Technology,Dalian 116024,China)
This paper summarizes the papers about the submerged structure vibration and acoustic radiation characteristics based on FEM or FEM/BEM published in China,emphasizes the numerical simulation on fluid,reviews and analyses the domestic research about the vibration characteristics of fluid-structure coupling,the acoustic radiation ofweak and strong coupling and the non-uniqueness and singularity problems of D-BEM and I-BEM,summarizes the research and the least development about the submerged structure vibration and acoustic radiation characteristics,and provides some reference to other researcherswho study the submerged structure vibration and acoustic radiation characteristics.
FEM;DBEM;IBEM;fluid-structure coupling;acoustic radiation;non-uniqueness;singularity
O326
A
10.3969/j.issn.1007-7294.2014.11.015
1007-7294(2014)11-1397-18
2014-06-05
国家自然科学基金资助项目(51079027)
王峥(1987-),男,硕士研究生,E-mail:zhwang@yahoo.cn;洪明(1959-),男,大连理工大学船舶工程学院教授,E-mail:mhong@dlut.edu.cn。

