潜艇浮筏隔振系统的半主动变结构控制
赵成(苏州市职业大学自动化系,江苏苏州215104)
潜艇浮筏隔振系统的半主动变结构控制
赵成
(苏州市职业大学自动化系,江苏苏州215104)
对带有电流变液智能阻尼器的双层浮筏隔振系统设计了一种半主动输出反馈变结构控制器。根据滑模运动方程稳定的Hurwitz判据选择滑模面矩阵。半主动控制条件限制电流变阻尼器可控阻尼力对隔振系统做负功,耗散振动能量。仿真分析了浮筏隔振系统在扫频激励信号下的力传递率及在双频激励信号下的输入力与输出力曲线。同时还仿真分析了双频激励信号作用下半主动静态输出反馈变结构控制下的双层浮筏隔振系统在系统参数出现摄动时的鲁棒性。仿真结果表明:半主动输出反馈变结构控制下的浮筏隔振系统的减振效果要远好于最优被动阻尼系统,对系统参数摄动也具有很强的鲁棒性。
半主动;变结构控制;浮筏;隔振系统
1 引言
浮筏是应用于船舰上的一种新型隔振降噪装置,它是把船舰中的马达、风机等多台动力设备弹性地安装在一个公共的筏架上,再将筏架弹性地安装在船身基础上。实际上,浮筏就是一种特殊的隔振系统,其机理是利用浮筏装置中弹性元件的阻尼和中间质量的设计来控制并衰减振动能量,使船舰表壳的振动减小。
从六十年代起,国内外许多学者在船舰的减振降噪方面进行了大量研究,提出了许多种方法并发表了相关论文[1-2]。近三十多年来,越来越多从事船舰设计的专家认为,船舰的减振降噪是一个急需解决的重要问题。降低舱室的振动和噪声不仅可以改善船舰上人员的居住和工作环境,重要的是能够保障船舰上精密仪器设备的正常运行,保证船舰的正常行使,特别是对于军用舰艇来说,能够增加其航行的稳定性和隐蔽性,提高战斗力。因此,改善船舰上浮筏隔振系统的减振性能是一个十分重要的问题。
半主动隔振系统在控制品质上接近于全主动隔振系统[3],且控制较为简单,能耗小。电流变阻尼器能够根据所加控制电压的不同而改变其阻尼力,转变过程迅速且可靠。本文将电流变阻尼器应用于浮筏隔振系统,同时考虑到电流变阻尼器存在的非线性特性及浮筏隔振系统模型参数的变化,有必要采取鲁棒控制策略[4-5]。常用的鲁棒控制策略有自适应控制法[6],变结构方法和H∞方法等。本文将变结构方法用于带有电流变智能阻尼器的浮筏隔振系统的控制,设计了一种半主动输出反馈变结构控制器,仿真了系统在扫频激励信号下的力传递率及在双频激励信号下的输入力与输出力曲线,同时还仿真分析了双频激励信号作用下半主动静态输出反馈变结构控制下的双层浮筏隔振系统在系统参数出现摄动时的鲁棒性,对控制效果进行了仿真评价。仿真结果表明半主动输出反馈变结构控制下的浮筏隔振系统的减振效果要好于最优被动阻尼系统,对系统参数摄动也具有很强的鲁棒性。
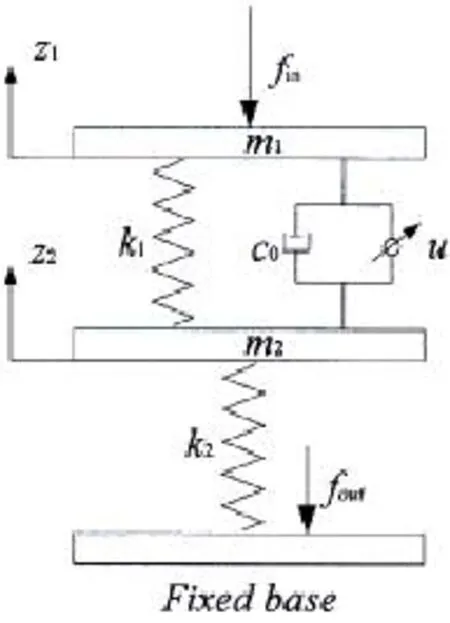
图1 浮筏隔振系统模型Fig.1 Themodel of floating raft isolation system
2 电流变智能阻尼器浮筏隔振系统
2.1 浮筏隔振系统模型
图1所示为带有电流变智能阻尼器的双层浮筏隔振系统模型。其中:m1、m2分别为上层质量、中间质量;k1、k2分别为初级隔振弹簧刚度、次级隔振弹簧刚度;z1、z2分别为上层质量受振后产生的位移、中间质量受振后产生的位移;fin为施加在上层质量上的竖直方向的激振力;fout为基座受到的振动力。
浮筏系统动力学方程为:
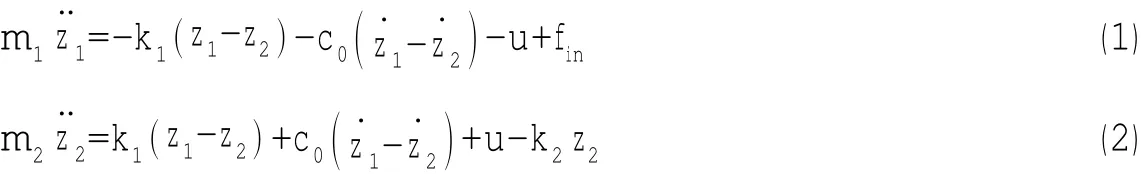
利用加速度传感器分别测量上层质量的加速度z¨1与中间质量的加速度z¨2,通过高通滤波器对低频噪声信号过滤,然后分别积分得到相应的绝对速度z˙1和z˙2;采用位移传感器测量相对位移z1-z2。
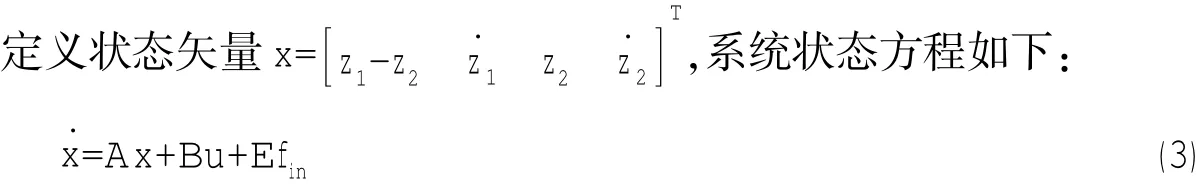

其中:
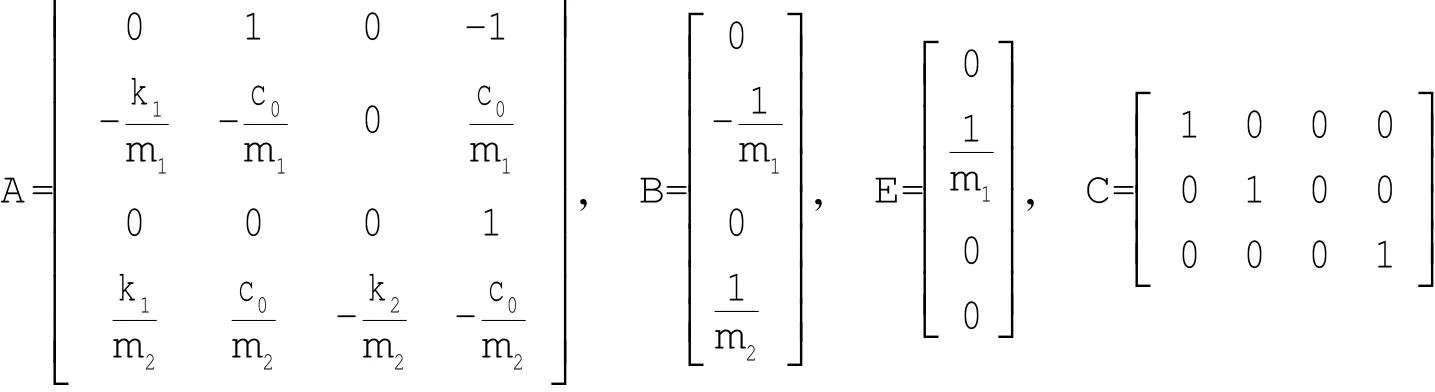
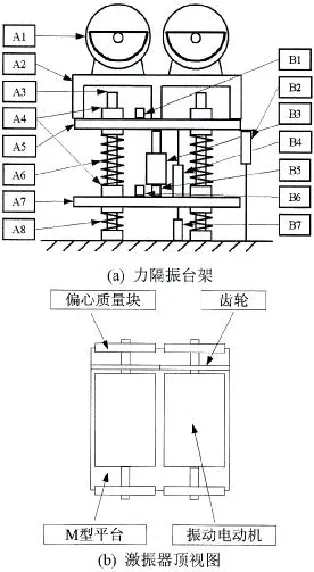
图2 力隔振台架Fig.2 Diagram of force isolation
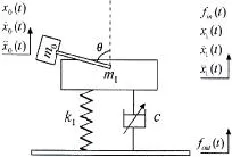
图3 力隔振台架激振力模型Fig.3 Mechanicalmodel of exciting force
2.2 浮筏隔振台架
本文针对动力设备振动力传递控制研究的要求,设计了相应的力隔振台架,如图2所示。
力隔振台架由激振器A1、上层板A5、初级隔振弹簧A6、中层板A7和次级隔振弹簧A8构成,并通过4个限位杆A3竖直地安装在基础之上,如图2所示。电流变阻尼器B3的活塞杆和外壳分别安装在上层、中层板的中间位置。激振器通过M形A2平台安装在上层板上,二者共同构成上层质量。中层板加上一定质量的配重,构成中间质量(图中略)。上层板和中层板上均装有线性轴承A4,以减小摩擦力。由于限位杆的作用,力隔振台架只能在竖直方向运动,因此构成一个典型的二自由度系统。如果将中间质量与基础紧固,系统就成为一个典型的单自由度系统。
力隔振台架上安装了多种传感器,可以测量各种物理量。其中,加速度传感器B1测量上层质量的竖直加速度,加速度传感器B6测量中间质量的竖直加速度。力传感器B5测量电流变阻尼器的输出力。位移传感器B2测量上层质量的绝对位移,位移传感器B7测量中间质量的绝对位移,位移传感器B4测量上层质量和中间质量的相对位移。
2.3 激振力分析
为克服现有力隔振台架单振动电机引起的非竖直方向的振动力和位移[7],本文设计的激振器由两台振动电动机组成。振动电动机的轴两端分别安装相同的偏心质量块。两台振动电机通过一对沿轴安装的齿轮同步运转。根据同步振动原理,在一台变频器的驱动下,两台振动电动机始终保持方向相反、相位对称的同步转动。4块偏心质量块产生的偏心力,在水平方向相互抵消,在竖直方向叠加。因此,激振器只提供竖直方向上的激振力,从而理论分析也大大简化。
图3中,m0为单个偏心质量块的质量。假设变频器控制电动机做匀速转动,角速度为ω。根据图3,在t时刻m0和m1在竖直方向的相对速度关系如下:

而

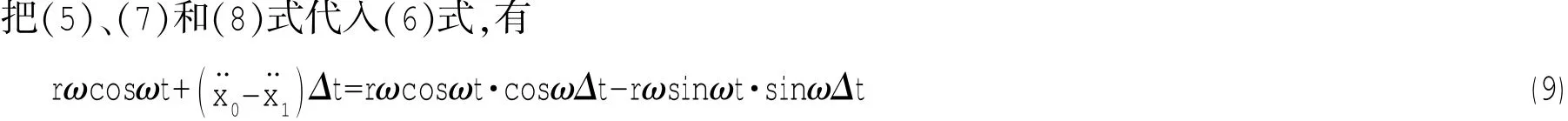

忽略偏振质量块的重量影响,则可以认为偏振质量块m0的竖直方向的加速度源自于上层质量体m1对它的作用力的竖直方向上的分量。根据牛顿第三定律,上层质量m1受到的竖直方向的激振力为:

(11)式表明,fint()实际上等于偏心力的竖直分量减去偏心质量块随上层质量一同运动的惯性力。
2.4 电流变阻尼器模型
根据Bingham模型,电流变阻尼器的阻尼力可表达为:F=c0x˙+u sgn);式中c0为零电场粘性阻尼系数;u为可控屈服阻尼力;x˙为活塞与缸体的相对速度。sgn()为符号函数。根据实验数据,拟合出可控阻尼力u与外加电压的关系式:

式中:U为电压,a0,a1,a2均为试验确定的常数。试验数据确定的常数:c0=1 013.4 Ns/m,a0=10.23 N,a1= 6.38 N·kV,a2=2.59 N·kV2。
图4给出了不同电压作用下阻尼力—活塞速度关系曲线。试验中活塞运动速度为15~100mm/s、激励幅值为60mm。增加电压,阻尼力增加。由图4可见,仿真结果与试验结果非常接近,表明上述阻尼器力学模型是合理的。
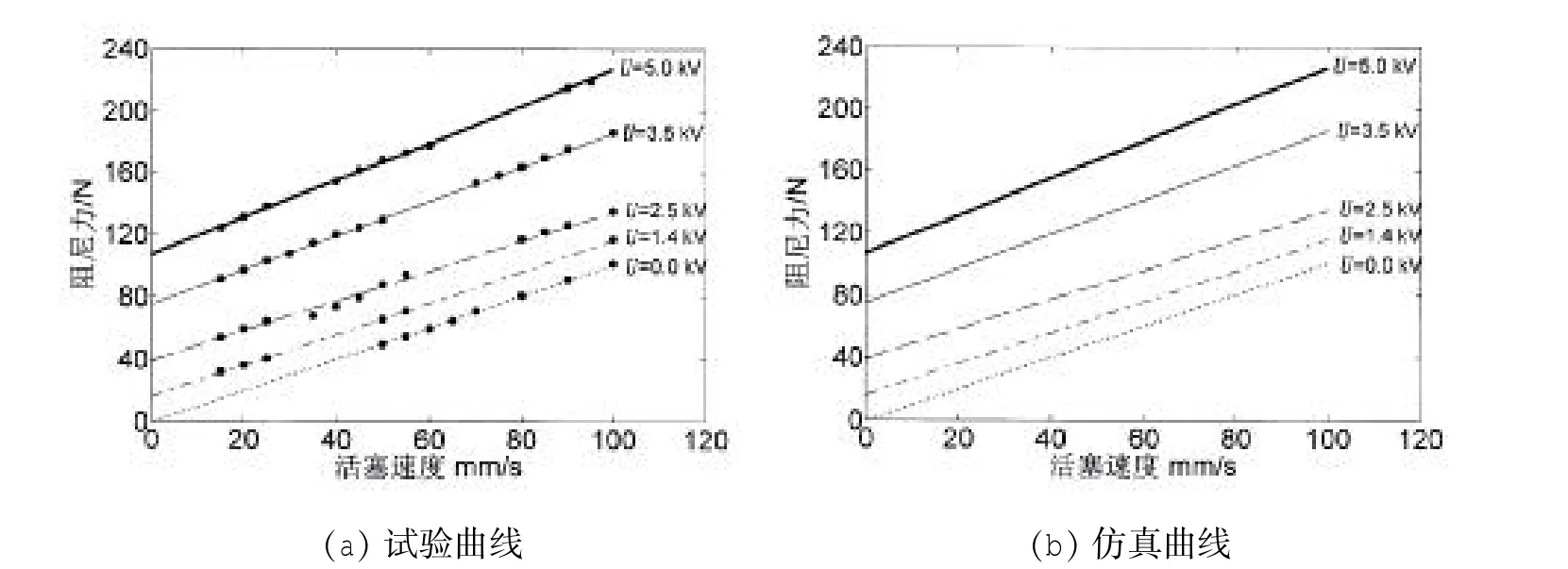
图4 不同电压作用下阻尼力—活塞速度关系曲线Fig.4 Damping force versus piston velocity at various voltages
3 浮筏隔振系统半主动输出反馈变结构控制器设计
3.1 输出反馈变结构控制设计条件
给定以下线性时不变系统:

其中:状态x∈Rn,控制u∈Rm,输出y∈Rl。假设A,B()可控,A,C()可观,且rank CB()=m。选择滑模面:

根据等效控制设计方法[8],在滑模面上有:

由(13)、(14)和(15)式及(16)式可得:

由(17)式得到等效控制:

将(18)式代入(13)式,得到滑动模态运动方程:

从(18)、(19)式可以看出,要使等效控制和滑动模态存在,就必须要求GCB()-1存在,即:

由(20)式可得:

上式要求传感器的数量至少要等于执行器的数量。
3.2 滑模面的设计
由线性系统理论知,由于A,B()可控,则可通过线性变换将(13)、(14)式变为以下简约型:
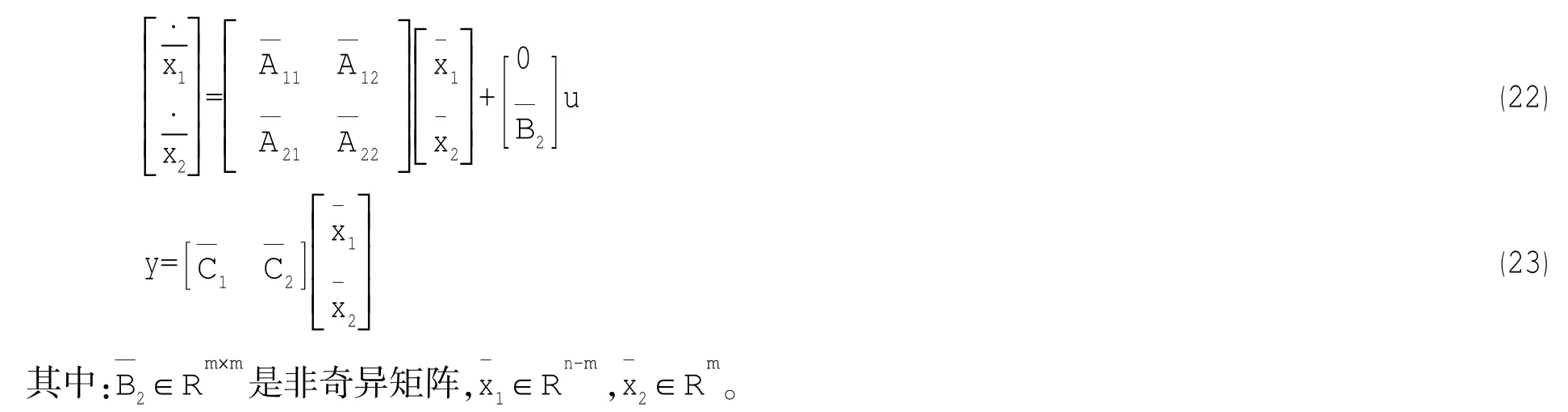
在滑模面上有:

由于要求(GCB)-1存在,所以也存在。
由(24)式得:

必须选择适当的矩阵G使得滑动模态运动方程(26)稳定。令:

可以用一般的线性系统输出反馈特征结构来设计H[9],然后再从(27)式解出G。G存在的充分必要条件是[10]:

3.3 输出反馈变结构控制器的设计
对本文所研究的电流变智能半主动浮筏隔振系统状态方程式(3)和(4),定义滑模面:

式中:G=g1g2g3[、是滑模面矩阵。
在进行滑模面的设计时,忽略(3)式中的外界激励fin,而在控制器的设计中加以考虑[11]。由于A,B()可控,则可通过线性变换:

将(3)、(4)式变为如(22)、(23)式所示的简约型,各分块阵为:
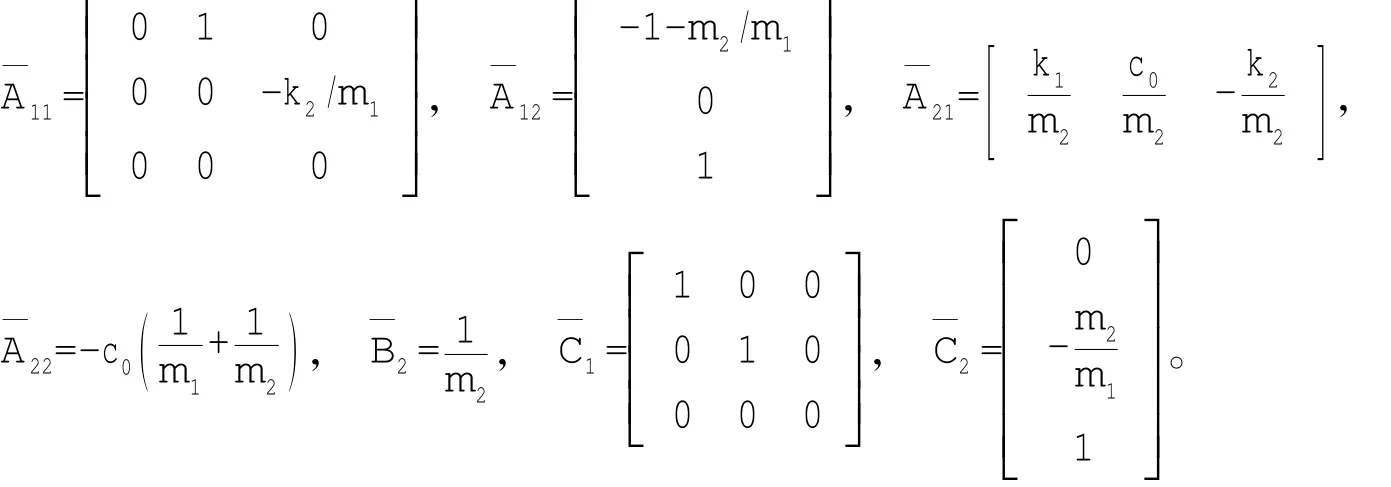
将降维滑动模态运动方程表示为(28)式的形式,式中:H=[h1h2h3、。

滑动模态运动方程(28)式的特征多项式为:

由滑动模态运动方程式(28)的Hurwitz稳定判据可以得到:

在(39)、(40)式的约束条件下,简单选取

本文所研究的浮筏隔振系统中,上层质量为中间质量的二倍。即:

由(42)、(43)式和(44)式得滑模面矩阵为:

由(43)、(45)式知,条件式(33)是成立的。
选取如下形式的控制律:

式中:k>0。
由滑模可达性条件STS˙<0有

从(47)式可以看出,如果CTGTGCA≤0,则选择N=0就可以使滑模可达性条件得到满足。
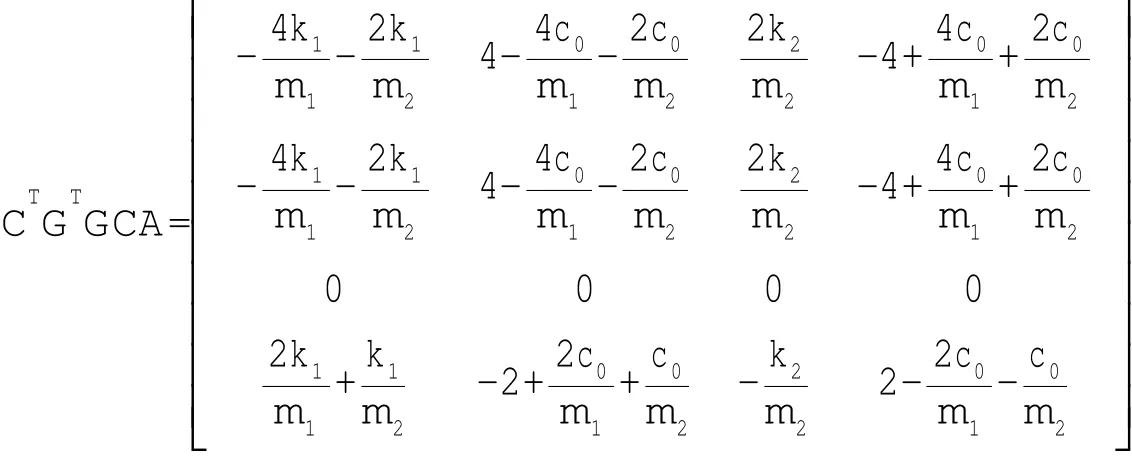
对于本文研究的电流变智能半主动浮筏隔振系统,由仿真实验中给出的系统参数可知是半负定的,所以我们选择

在控制律的表达式(46)中包含了前馈补偿,即:-GCB()-1GCEfin。对于我们研究的实际的减振系统,上层质量的加速度、上层质量与中间质量的相对位移以及电流变阻尼器的阻尼力是可以检测得到的,根据浮筏系统动力学方程(1),激励力fin是容易通过下式确定的。

(49)式中的F为力传感器测量得到的电流变阻尼器的阻尼力。
由(48)式,控制律(46)式变为:

3.4 饱和约束条件
由于最大可控阻尼力受到电流变阻尼器具体的结构形式限制,只能是一个有限值。所以在输出反馈变结构控制电流变阻尼器隔振系统中引入饱和非线性控制环节,表示为:

3.5 半主动控制条件
根据图1,fout=k2z2为基座受到的振动力,即浮筏隔振系统的输出力。对于我们所研究的双层浮筏隔振系统,要求电流变阻尼器可控屈服阻尼力只能对隔振系统做负功,耗散中间质量体m2的振动能量,相应的半主动控制策略为:

在确定了可控屈服阻尼力后,结合(12)式所确定的电流变阻尼器的外加电压为:

综合上面的分析,电流变阻尼器浮筏隔振系统控制框图如图5所示。
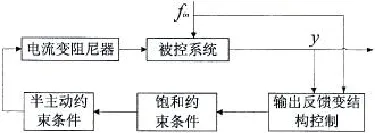
图5 控制系统框图Fig.5 Controlblock diagram of semi-active floating raft isolation system
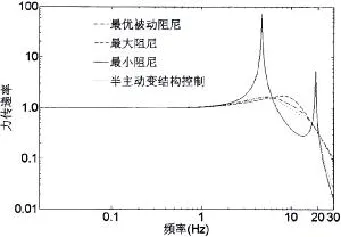
图6 扫频信号激励下隔振系统力传递率Fig.6 Force transmissibility of semi-active floating raft isolation system to sweep-frequency signal
4 仿真实验
在上述控制律基础上,运用Matlab7.0对系统进行仿真,仿真实验中的参数如下:
m0=3.2 kg,m1=32 kg,m2=16 kg,
c0=1 013.4 N S/M,r=0.002m,
k1=33 000 N/m,k2=185 000 N/m,
copt=1 453 N s/m,Umax=5 kV,
a0=10.23 N,a1=6.38 N·kV,
a2=2.59 N·kV2。
备注:copt为最优被动阻尼。
4.1 扫频信号输入
输入信号为频率0-30 Hz的扫频信号,扫频时间为30 s。
图6为单个扫频信号激励下隔振系统力传递率曲线。为了更好地说明隔振系统在半主动输出反馈变结构控制下的减振效果,图中同时给出了隔振系统在无控制作用的最小阻尼、最优被动阻尼及最大阻尼情况下的力传递率。从图6中可以看出,半主动输出反馈变结构控制下的双层力隔振系统的控制效果要好于最优被动系统,它减低了基座受力,提高了船舰行使的安全性。
4.2 双频激励
激励信号由两个单频信号合成得到,信号的形式为:2
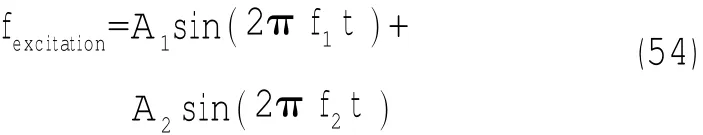
隔振系统的一阶共振频率与二阶共振频率约为5 Hz,16 Hz。从(11)式可以看出,在同一个输入激励信号作用下,对无控制作用的最优被动阻尼系统与半主动输出反馈变结构控制下的隔振系统来说,由于所产生的上层质量的加速度是不同的,所以对两个系统所产生的输入激励力是不同的,因而不能单独以两个不同系统在同一个输入激励信号作用下的输出力响应曲线来判断各个系统的隔振效果。为此,本文仿真给出了无控制作用的最优被动阻尼系统与半主动输出反馈变结构控制下的隔振系统在以下双频激励信号下的输入力及输出力曲线,持续时间都为2 s。
图7为双频信号激励下最优被动阻尼系统与半主动输出反馈变结构控制下的隔振系统的输入力及输出力响应曲线。图8为系统参数发生摄动时(Δm1=-0.1m1,Δk1=-0.1k1及Δk2=-0.1k2)双频信号激励下最优被动阻尼系统与半主动输出反馈变结构控制下的隔振系统的输入力及输出力响应曲线。从图7及图8中可以看出,无论系统参数是否发生摄动,相对于最优被动阻尼系统的输出力比输入力幅度的降低,半主动输出反馈变结构控制下的隔振系统的输出力比输入力有更大幅度的减小,为此说明半主动输出反馈变结构控制下的隔振系统减振效果要明显好于最优被动隔振系统。
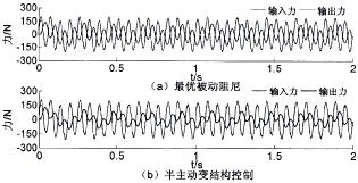
图7 双频信号激励下的输入力及输出力响应曲线Fig.7 Input force and output force response to dual-frequency signal excitation
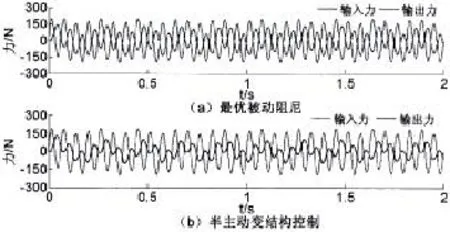
图8 系统参数摄动时(Δm1=-0.1m1,Δk1=-0.1k1及Δk2=-0.1k2)双频信号激励下的输入力及输出力响应曲线Fig.8 Input force and output force response to dual-frequency signal excitation with parameter uncertainties(Δm1=-0.1m1, Δk1=-0.1k1andΔk2=-0.1k2)
5 结语
运用变结构控制方法设计了带有电流变阻尼器的双层浮筏隔振系统的半主动输出反馈变结构控制器。仿真分析了浮筏隔振系统在扫频激励信号下的力传递率及在双频激励信号下的输入力与输出力曲线。同时还仿真分析了双频激励信号作用下半主动静态输出反馈变结构控制下的双层浮筏隔振系统在系统参数出现摄动时的鲁棒性。从仿真结果看,无论系统参数是否发生摄动,半主动输出反馈变结构控制下的浮筏隔振系统的隔振效果要好于最优被动系统,使基座受力得到明显降低,提高了船舰行使的安全性。
参考文献:
[1]许树浩,桂洪斌.浮筏系统隔振性能的功率流评价指标[J].船舶力学,2012,16(5):567-572. Xu Shuhao,Cui Hongbin.Power flow estimation of float raft isolation system[J].Journal of Ship Mechanics,2012,16(5): 567-572.
[2]张树桢,陈前.柔性浮筏隔振系统的理论建模与仿真研究[J].船舶力学,2012,16(10):1187-1198. Zhang Shuzhen,Chen Qian.Modeling and simulation research on flexible floating raft isolation system[J].Journal of Ship Mechanics,2012,16(10):1187-1198.
[3]Choi SB,Kim W K.Vibration control of a semi-active suspension featuring electrorheological fluid dampers[J].Journal of Sound and Vibration,2000,234(3):537-546.
[4]张孝祖,武鹏,黄少华.基于模糊鲁棒控制的车辆半主动悬架性能分析[J].农业机械学报,2006,37(5):1-4.
[5]方敏,史明光,陈无畏.汽车主动悬架多目标H2/H∞混合控制[J].农业机械学报,2005,36(3):4-7.
[6]Youn I,Hac A.Semi-active suspension with adaptive capability[J].Journal of Sound and Vibration,1995,180(3):475-492.
[7]汪建晓,孟光.磁流变液阻尼器用于振动控制的理论及实验研究[J].振动与冲击,2001,20(2):39-45.
[8]Andry A N Jr,Shaprio E Y,Chung JC.Eigenstructure assignment for linear system[J].IEEE Transaction on Aerospace Electronic Systems,1983,19(5):711-729.
[9]Heck B S,Ferri A A.Application of output feedback to variable structure systems[J].Journal of Guidance Control and Dynamics,1989,12(6):932-935.
[10]Elbeheiry EM.Effects of small travel speed variations on active vibration control inmodern vehicles[J].Journal of Sound and Vibration,2002,232(5):857-875.
[11]Yang JN,Wu JC,Li Z.Control of seismic-excited buildings using active variable stiffness systems[J].Engineering Structures,1996,18(8):589-596.
Sem i-active variable structure control for floating raft isolation system
ZHAO Cheng
(Dept of Automation,Suzhou Vocational University,Suzhou 215104,China)
A semi-active output feedback variable structure controller is designed for floating raft isolation system with electro-rheological(ER)damper.Sliding surfacematrix is selected in accordancewith Hurwitz stable judgementof slidingmodemotion equation.The optimal vibration attenuation is guaranteed due to the control rule that damping force only dissipates the vibration energy of isolation system.The force transmissibility under conditions of sweep-frequency signal,input force and output force for the floating raft vibration isolation system under conditions of dual-frequency exciting signal are simulated,respectively.The robustness of the controlmethod with respect to parameter variations is simulated.The simulation results indicate that the performance of floating raft vibration isolation system designed by semi-active output feedback variable structure controlmethod is remarkably better than those of optimally passive damping even if system parameter uncertainties exist.
semi-active;variable structure control;floating raft;isolation system
O328 TB535
A
10.3969/j.issn.1007-7294.2014.11.012
1007-7294(2014)11-1367-10
2014-05-12
国家自然科学基金资助项目(69974024)
赵成(1974),男,博士,E-mail:zhaoch@wxit.edu.cn。

