岛礁波浪环境下浮式结构物的动响应预报
田超,丁军,杨鹏(中国船舶科学研究中心,江苏无锡214082)
岛礁波浪环境下浮式结构物的动响应预报
田超,丁军,杨鹏
(中国船舶科学研究中心,江苏无锡214082)
中国南海海洋岛礁往往都环绕着宽度数百到数千米、水深很浅的珊瑚礁盘,这些礁盘不仅具有丰富的渔业和旅游资源,而且发挥着消波、护岛的重要作用。为开发海洋资源,可以在岛礁附近布设各种浮体结构物,作为海洋开发、渔业生产、环境旅游等综合保障基地。对于岛礁附近的浮式结构物,其动响应特征必将受到周围复杂的近岛礁海洋环境的影响。文章采用缓坡方程考虑近岛礁波浪环境影响,以半潜式平台为研究对象,开创性地提出了一种工程简化计算方法,用于预报岛礁附近浮式结构物在波浪中的运动与载荷响应,为后续岛礁中型浮体的设计和安全性评估提供了分析手段。
岛礁影响系数;浮式结构物;运动响应;波浪载荷
1 引言
我国南海海洋岛礁周边往往都环绕着宽度数百到数千米、水深很浅的珊瑚礁盘,这些礁盘不仅具有丰富的渔业和旅游资源,而且发挥着消波、护岛的重要作用。为开发海洋资源,可以在岛礁附近布设各种浮体结构物(如图1),作为海洋开发、渔业生产、环境旅游等综合保障基地。对于岛礁附近的浮式结构物,一方面岛礁附近复杂的海底条件将对波浪的传播和变形产生较大的影响,另一方面浮式结构物的动响应特征也将受到周围复杂海洋环境的影响,因此在近岛礁浮式结构物的设计建造与安全性评估中,考虑岛礁波浪环境对浮式结构物动响应特性的影响将显得特别重要。

图1 近岛礁海上浮式结构物Fig.1 Ocean floating structures near islands and reefs
当波浪从深远海传播到岛礁附近,由于其复杂的地形地貌,波浪将发生折射、绕射和反射等,当波浪变陡到一定限度后,便产生破碎。精确模拟波浪这一系列变化是十分复杂和困难的,目前国内外学者[1-3]在波浪数值模型的研究和应用方面取得了很大的进展,通过建立波浪的数学模型,可以求解波浪在不同地形上传播、折射、绕射、越浪、增减水和破碎等问题。这些模型主要可以划分为三种:缓坡方程模型、Boussinesq方程模型和动谱平衡方程模型。目前对于浮式结构物的动响应,许多学者[4-9]已进行了多年的研究,但是考虑我国南海岛礁海洋和地质环境,分析近岛礁浮式结构物动响应的研究成果却很少。本文基于缓坡方程和三维水动力学理论模型,开创性地提出了一种工程简化计算方法,在完成典型岛礁附近波浪场数值模拟基础上,以半潜式平台为对象,预报了岛礁附近浮式结构物在波浪中的运动与载荷响应,为后续岛礁中型浮体的设计和安全性评估铺平了道路。
2 近岛礁波浪场数值模拟
2.1 方案地形
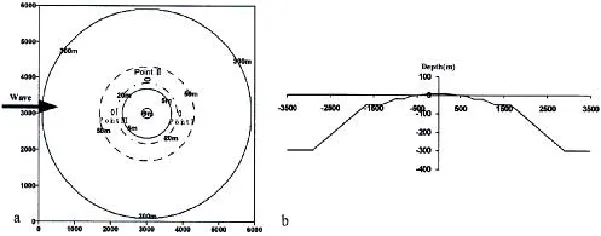
图2 典型岛礁地形图(a)海底等深线图;(b)水深中剖面图Fig.2 A typical landform of island and reef(a)Bathymetrical contours;(b)Water depth of cross section
本文选定一典型简化的岛礁地形,岛半径为150m;5m水深区域距离岛中心的范围为150~650m,宽度为500 m;20 m水深区域距离岛中心范围为830~1 000m,宽度为170m,其中5 m水深到20 m水深之间用1:10的坡度进行过渡;50m水深区域距离岛中心范围为1 300~1 650m,宽度为350m,其中20m水深到50m水深之间用1:10的坡度进行过渡;深水区取300m,距离岛中心范围为2 900m,其中50m水深到300m水深用1:5的坡度进行过渡。计算方案总面积为6 000m×6 000m,图2(a)给出了主要的海底等深线示意图及相应的计算点位置,波浪方向如图中所示,即从图中左侧向右侧传播。为了对浮式结构物在岛礁不同布设位置处的水动力性能比较,选取三个位置(Points I,II,III)进行讨论,相对于来波方向,Point I位于岛礁的后侧,Point II位于岛礁的上侧,Point III位于岛礁的前侧。图2(b)为海底地形中横剖面水深示意图。
2.2 近岛礁波浪场数值模拟
(1)缓坡方程模型
外海波浪传入近岸浅水时,受多种因素的影响,将产生一系列复杂的变化,考虑波能损耗和风能输入的推广的缓坡方程形式如下[10]:定常:
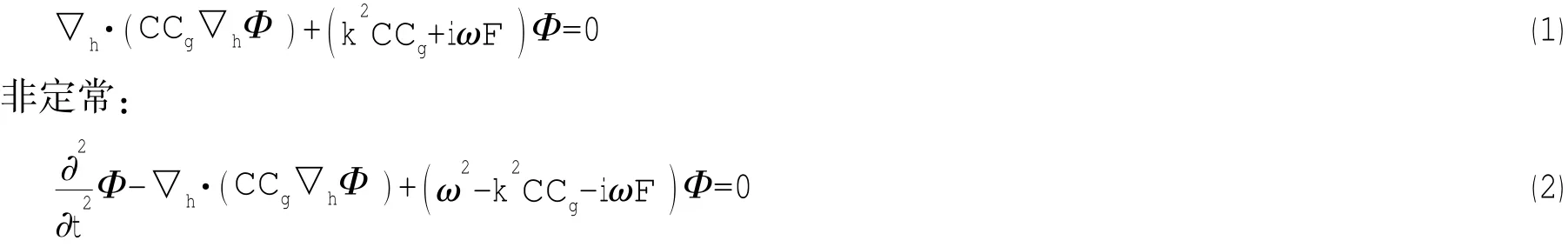
式中:C、Cg分别表示波速和波群速,Φ表示波势,k表示波数,ω为角频率,F为波能变化因子,i=。
(1)式为变系数椭圆型方程,(2)式为双曲型方程,直接求解比较困难,本文采用含松弛因子的ADI法求解(1)式和(2)式,可大大提高计算的收敛速度和稳定性,并能够快速得到稳定、精确的岛礁附近水域的波高分布结果。
(2)规则波计算结果
给定深水区域的入射正弦波H=1m,计算波周期区间取5~20 s,假定波从深水向浅水传播过程中频率不变,由于受到岛礁的影响,波浪在传播过程中将发生浅水变形、折射和绕射等一系列变化,图3给出了H=1m,T=12 s时的波浪传播变形图。
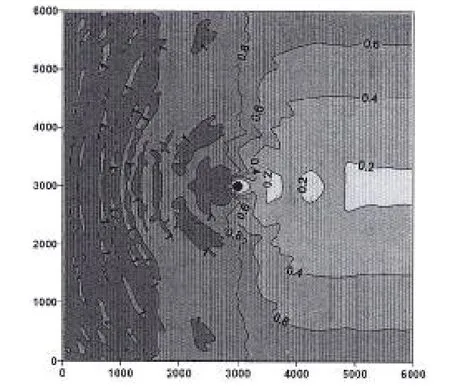
图3 规则波波浪场计算结果Fig.3 Results of regularwave field
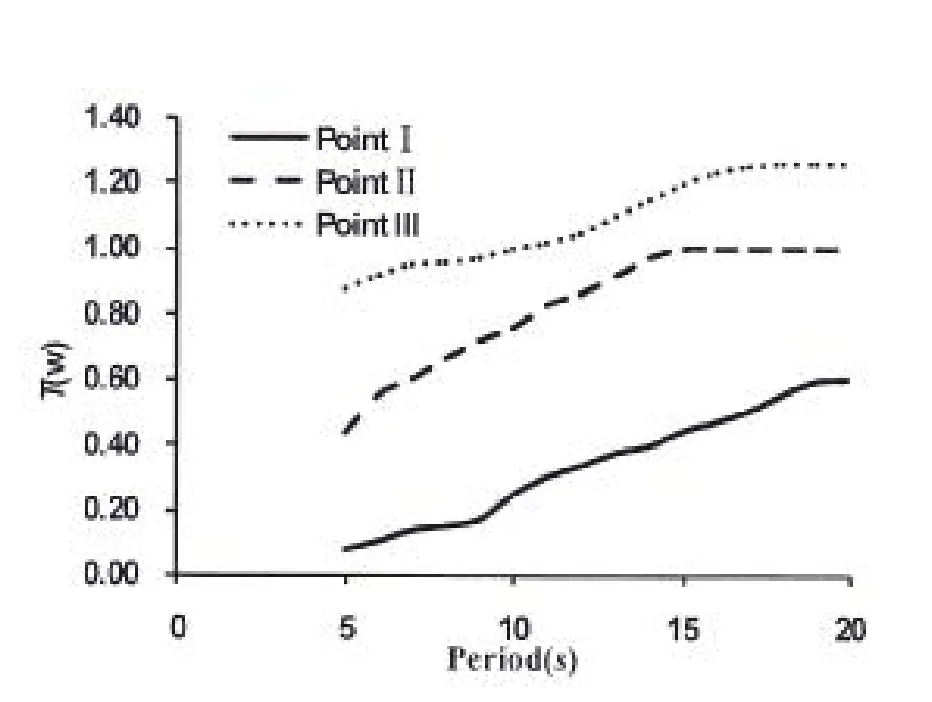
图4 三个计算点处的岛礁影响系数Fig.4 Influence coefficient of islands and reefs in three points
本文定义岛礁影响系数Tω()=H’/H,其中H为远场规则波的波高,H=1 m,H’为考虑岛礁影响后,频率为ω,波高为1.0的远场规则波传播到计算点时的波高。图4给出了不同周期下,三个计算点处的岛礁影响系数Tω()。由计算结果可以看出:1)对于同一个计算点,如PointⅠ,随着波浪周期的变大,波浪传播的绕射作用变得更加明显,从而使得该点处的波高也逐渐增大;2)对于不同计算点,岛礁对PointⅠ的遮蔽效应更加明显,从而使得PointⅠ处的波高明显小于另外两点,PointⅡ处在入射波周期大于14 s后的波高都为1.0m即等于入射波高,而PointⅢ位于岛礁的前侧,由于反射波的影响,使得该点处的波高在10 s之前略小于入射波,而10 s之后却明显大于入射波。
(3)不规则波计算结果
不规则波计算时采用适用于有限风区情况的JONSWAPS谱,如(3)式所示:

深水区根据文献[11]中选取入射波高Hs=5.0m,ωp=0.705 rad/s(Tp=8.91 s),则得到近岛礁波浪场的计算结果见图5,图6给出了入射波、PointⅠ、PointⅡ和PointⅢ处的频谱图。从图中可以看出,岛礁对波浪的传播变形影响十分显著,在岛礁的前方,发生了波浪反射现象,从而导致岛礁正前方PointⅢ处的波高大于入射波高,同规则波类似,由于岛礁的遮蔽效应,导致PointⅠ处波高要明显小于PointⅡ和PointⅢ处。
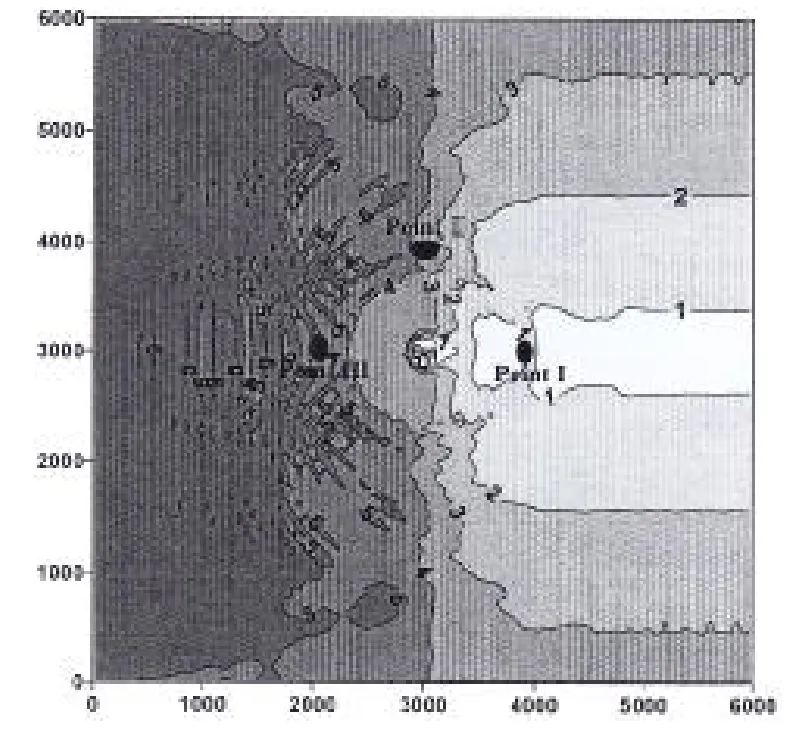
图5 不规则波波浪场计算结果Fig.5 Results of irregular wave field
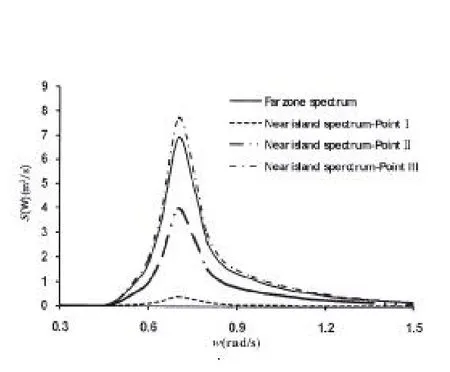
图6 入射波及三个计算点处的频谱图Fig.6 Spectrum of incidentwave and three points
3 平台运动及载荷传递函数
3.1 无岛礁及岛礁影响下平台运动及载荷传递函数
文中以一半潜式平台为研究对象,该半潜式平台由上部箱型甲板、中间六根立柱、下部三个浮筒及4根横撑组成,总长50m,宽20m,高12m,吃水5m,排水量2 500 t,平台模型和水动力计算网格见图7。

图7 半潜式平台(a)平台模型(b)水动力计算网格Fig.7 Semi-submersible platform(a)Model of platform(b)Hydrodynamic panelmodel
根据三维线性波浪载荷理论可以得到半潜平台在20m水深不受岛礁影响情况下的运动及载荷响应传递函数,当考虑岛礁影响时,本文提出将岛礁影响系数Tω()(见图4)乘以无岛礁存在浅水条件下的运动和载荷传递函数,得到考虑岛礁影响后,近岛礁平台的运动和载荷响应传递函数:

式中:Tω()为岛礁影响系数;H0ω()为无岛礁存在的传递函数,得到岛礁影响下平台运动及载荷传递函数。

图8 垂荡运动传递函数Fig.8 RAO of heave
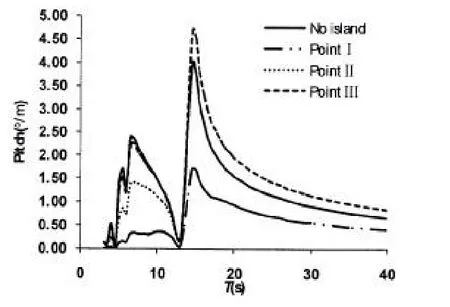
图9 纵摇运动传递函数Fig.9 RAO of pitch
图8 ~10分别给出了平台布置在三个计算点处的不考虑岛礁和考虑岛礁影响后的运动及载荷响应传递函数。从图中可以看出考虑岛礁影响后半潜平台运动和载荷响应的传递函数与未考虑岛礁时相比存在明显的差别,对于PointⅠ处,平台运动和载荷响应传递函数的差别主要体现在5~25 s之间,PointⅡ处差别主要体现在5~15 s之间,PointⅢ处在12 s之前略微减小,然后有所增大,这基本与图4中的计算结果相对应。
3.2 岛礁影响下平台运动及载荷短期预报
短期海浪可视为均值为零的平稳正态随机过程。响应谱SW与海浪谱Sζ之间可以通过下式联系:
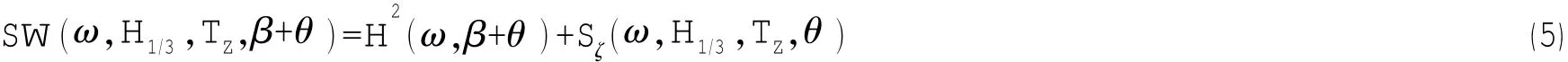
式中:Hω,β+θ()为系统传递函数的模。
为进一步比较分析岛礁对平台响应的影响,文中采用两种方法来预报近岛礁情况下平台各响应参数的短期响应结果:1)远场波浪谱+近岛礁传递函数,即通过在平台运动及载荷响应传递函数中考虑岛礁影响系数,来考虑岛礁的影响;2)远场传递函数+近岛礁波浪谱,即通过考虑岛礁存在对平台所在位置波浪谱的影响,来计入岛礁的影响;3)另外,为对比讨论岛礁的影响,本文还采用远场波浪谱和无岛礁存在的传递函数,即不考虑岛礁的影响,给出了平台运动及载荷的短期响应,并与前面两种方法结果进行比较。
波浪远场谱、Point I、PointⅡ和PointⅢ处的近场波谱见图6,计入岛礁存在影响和不考虑岛礁存在影响时的平台运动及载荷响应传递函数见图8~10,假设短期响应服从Rayleigh分布,可以得到运动与载荷响应的短期有义值,如表1所示。从表中可以看出:1)对于平台的运动响应,方法1和方法2计算得到Point I的垂荡相较于方法3分别减小了77.8%和76.0%,Point II分别减小了15.7%和12.0%,PointⅢ分别增大了3.1%和6.1%,说明平台的布置位置对运动响应短期预报结果影响较大。平台纵摇运动响应的变化规律基本与垂荡类似;2)对于平台的中横剖面垂向弯矩响应,方法1和方法2计算得到Point I的响应相较于方法3分别减小了77.7%和76.0%,Point II分别减小了14.1%和11.9%,这与平台运动响应的变化规律较为一致。而PointⅢ方法1相对于方法3减小了5.4%,方法2相对于方法3增加了4.5%,这主要因为规则波岛礁影响系数在平台中横剖面垂向弯矩传递函数的峰值(T=7 s)附近时小于1,而不规则波波浪谱在此处是大于远场波浪谱的,从而导致两种方法出现一定的差异;3)上述计算结果表明,方法1和方法2相对于方法3存在着较大的差异,说明岛礁对平台运动及载荷响应的短期预报结果有着较大影响,而方法1和方法2之间的差异较小,一般在3%左右,最大不超过10%,说明这两种方法具有一定可比性,可以用来对岛礁周围浮式结构物的动响应进行预报。
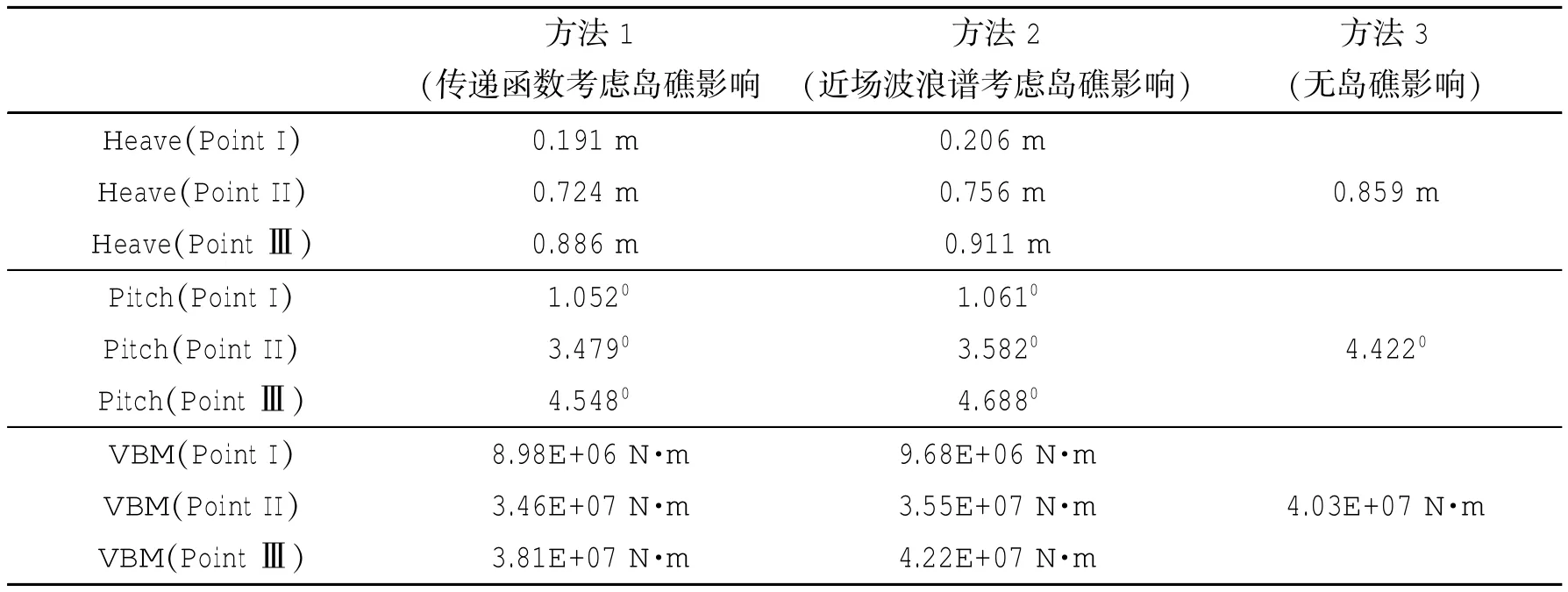
表1 平台运动与载荷的短期有义值Tab.1 Short term significant values ofmotions and loads
3.3 岛礁影响下平台波浪载荷长期预报
根据表2所示的南海区块S3的海浪资料[12],对半潜式平台的中横剖面垂向弯矩进行线性长期预报。图11给出了无岛礁情况下和当平台布置在Point I、Point II和PointⅢ处时的平台中横剖面垂向弯矩长期预报结果,结果表明载荷水平与负对数超越概率之间基本呈线性关系,且岛礁的存在和平台在岛礁周围的布放位置对长期预报结果影响很大,表3列出了当-log P()等于2、4、6和8时对应的长期预报结果,当取平台一生中遭遇的波浪载荷循环数n=108,则对应概率水平-log P()=8时,Point I处相对于无岛礁情况下减小了86.6%,Point II处相对于无岛礁情况下减小了40.0%,PointⅢ处相对于无岛礁情况下减小了5.6%,由此也发现岛礁对浮式结构物载荷长期预报结果的影响十分明显。
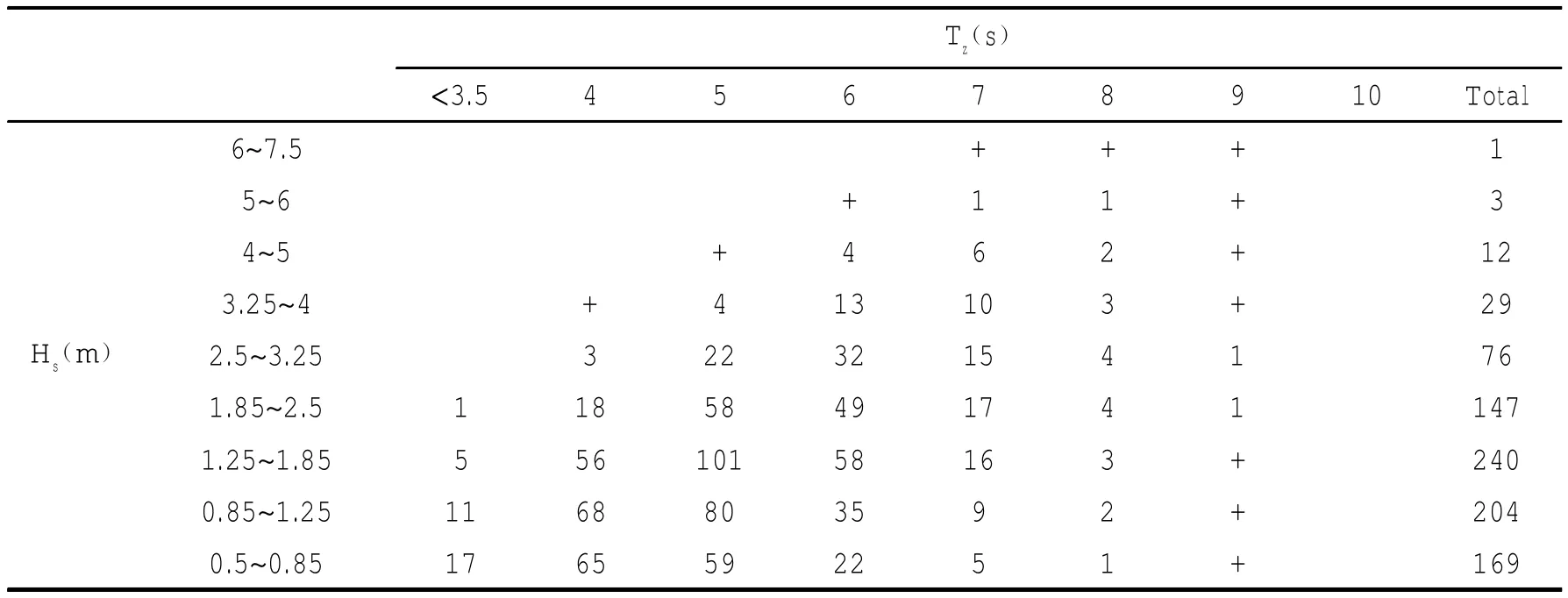
表2 南海区块S3的海浪统计资料Tab.2 W ave statistics of Nanhai S3 district

续表1

表3 平台中横剖面垂向弯矩长期预报结果(N·m)Tab.3 Results of long term prediction of vertical bendingmoment in m idship section
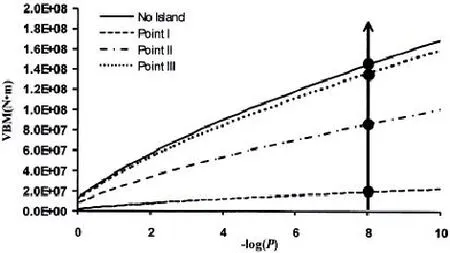
图11 平台中横剖面垂向弯矩长期预报Fig.11 Long term prediction of vertical bendingmoment inmidship section
4 结论
远海波浪传播到岛礁附近时,受岛礁周围复杂的地形影响,将产生一系列复杂的变化,对于布置在岛礁附近的浮式结构物,其动响应特征也将受到岛礁附近复杂海洋环境的影响。本文采用缓坡方程考虑近岛礁波浪环境影响,提出了岛礁影响系数,并以半潜式平台为研究对象,开创性地提出了一种近岛礁浮式结构物的动响应工程预报方法,并给出了考虑岛礁影响后的半潜式平台运动及载荷的传递函数、短期和长期预报结果。结果表明:1)岛礁存在及平台在岛礁周围的布置位置对平台运动和载荷响应的影响非常大,在对近岛礁浮式结构物的运动和载荷响应进行预报时,必须考虑岛礁的影响;2)经过计算分析,通过考虑岛礁影响系数,可以用来对岛礁周围浮式结构物的动响应进行预报,后续将考虑岛礁环境影响,开展半潜平台模型试验,对本文提出的方法进行验证,并为后续岛礁中型浮体的设计和安全性评估提供指导。
参考文献:
[1]Berkhoff JCW.Computation of combined refraction-diffraction[C].Proceedings of the 13th International Conference on Coastal Engineering,ASCE,1972:745-747.
[2]李孟国,蒋德才.近岸波浪传播折射变形的数学模型综述[J].海岸工程,1999,18(4):100-109.
[3]冯芒,沙文钰等.近岸海浪几种数值计算模型的比较[J].海洋预报,2003,20(1):52-59.
[4]吴有生,杜双兴.极大型海洋浮体结构的流固耦合分析[J].舰船科学技术,1995,139(1):1-9.
[5]王志军.箱式超大型浮体结构的水弹性响应研究[D].上海:上海交通大学,2001.
[6]陈徐均.浮体二阶非线性水弹性力学分析方法[D].无锡:中国船舶科学研究中心,2001.
[7]CuiWeicheng,Yang Jianmin,Wu Yousheng,Liu Yingzhong.Theory of Hydroelasticity and Its Application to Very Large Floating Structures[M].上海:上海交通大学出版社,2007.
[8]宋皓.超大型浮体在非均匀海洋环境下的水弹性响应研究[D].上海:上海交通大学,2004.
[9]孙辉,崔维成,刘应中.超大浮体在二维不均匀底部上的水弹性响应[J].上海交通大学学报,2003,37(8):1172-1175.
[10]王红川.缓坡方程的改进及其推广应用[D].南京:河海大学,2007.
[11]叶永林.南海(西沙群岛)海洋环境、地质地貌调研报告[R].无锡:中国船舶科学研究中心,2013.
[12]方钟圣.西北太平洋波浪统计集[M].北京:国防工业出版社,1996.
Prediction of dynam ic responses of floating structures under wave environment near islands and reefs
TIAN Chao,DING Jun,YANG Peng
(China Ship Scientific Research Center,Wuxi214082,China)
The islands in South China Sea are usually encircled by coral table reefs which play an important role in wave absorbing and protecting islands.Fishing and tourism resources are abundant near the coral reefs,stretching with hundreds to thousandsmeters in shallow water.The floating structures can be disposed near the islands and reefs as comprehensive support bases for ocean development,fishery production and tourism.The responses of the floating structureswill be influenced by the complex ocean environment near islands and reefs.Taking the example of a semi-submersible platform,the influence of ocean waves near islands and reefs is considered based on themild-slope equation.A simplified engineeringmethod is originally proposed to predict themotion and load of floating structures near islands and reefs,which can be used in the design and safety assessmentof floating structures near islands and reefs.
islands and reefs effect ratio;floating structures;motion responses;wave loads
U661.4
A
10.3969/j.issn.1007-7294.2014.11.002
1007-7294(2014)11-1284-08
2014-07-22
国家重点基础研究发展计划资助(2013CB036100)
田超(1978-),男,博士,中国船舶科学研究中心高级工程师,Email:ctian@cssrc.com.cn;丁军(1986-),男,中国船舶科学研究中心工程师。

