基于下记录值样本的指数分布族参数估计
许 莹
(长春大学旅游学院 基础部,吉林 长春 130607)
1 引言
记录值被给出至今已有近百年的历史,当记录值第一次被给出时,曾轰动一时,全球各界科研工作者对其展开了猛烈的研究[1].计算机、竞技体育、天气预报以及人类生理极限等不同领域均有记录值的身影,并且记录值所起到的作用也是有目共睹.Chandle.K.N于1952年首次将记录值同统计学联系起来,由于早前统计领域中记录值的应用时间较短,因此大多数学者仅在经典统计理论中应用记录值[2].近几年,许多学者研究了基于记录值模型参数的Bayes估计,但只局限在对上记录值的研究,对于下记录值的研讨还较为空白.笔者基于下记录值样本,对指数分布族参数进行讨价,现报告如下.
定义1 设连续分布函数F(x;θ)的样本为X1,X2,…,Xn,俩俩相互独立,f(x;θ)是其密度函数.对任意n≥1,令L(1)=1,L(n+1)=min{j:j>L(n),Xj>XL(n)},则{XL(n)}({L(n)})称为这个序列的一个下记录值(下记录时间).
2 指数族的选取
选用F(x;θ)=[g(x)]θ,且B≥x≥A,θ>0为分布函数,因为F'(x;θ)=f(x;θ),所以指数族的密度函数是:f(x;θ)=θg'(x)g(x)θ-1,且B>x>A,θ>0.
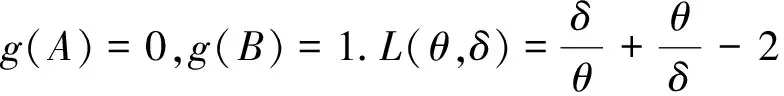
3 Bayes估计
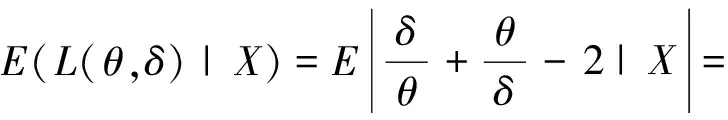
引理2 如果统计判决问题的损失函数是X~f(x;θ),θ∈Θ,L(θ,δ),π(θ)是θ的先验分布,所以当下面两点成立,①若关于δ,L(θ,δ)是严凸损失函数,在此统计判决问题几乎处处有惟一的Bayes解.②若θ具有惟一的Bayes估计,那么此估计是容许的.
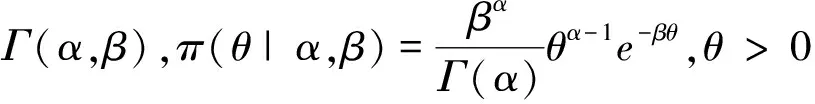
证明 由于参数θ的共轭先验分布是伽玛分布Γ(α,β),那么我们容易知道
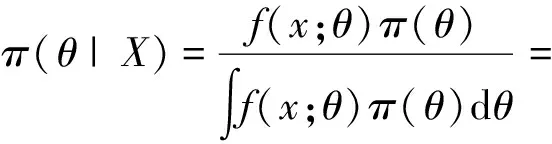
又由于T=T(XL(n))=-lng(XL(n)),所以,lng(x)=-t,g(x)=e-t,g'(x)=-e-1,
即可知,

故
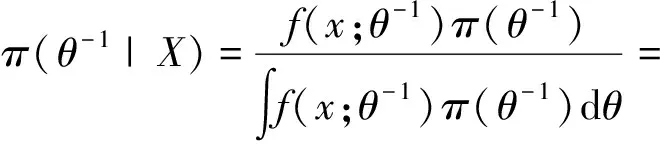
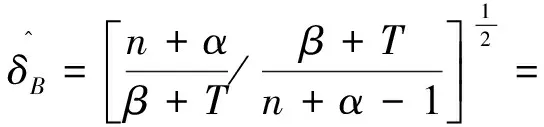

4 经验Bayes估计
假定超参数α已知,且超参数β为未知,下记录值样本为XL(1),XL(2),…XL(n),这样我们可以得到边缘密度函数,即
由于T=T(XL(n))=-lng(XL(n)),所以lng(x)=-t,g(x)=e-t,g'(x)=-e-1,故

因为在P(x|β)下我们可以得到β的极大似然估计,即

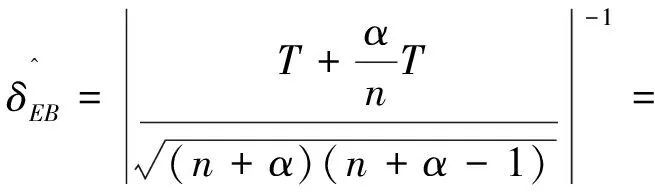
5 结论
由于记录值减少了样本数量,使得在计算更简单的前提下得到同样精准的结果,如此优越的性质,让各领域学者对记录值的认知也越来越深厚,并且把它推广到更广阔的领域[3].近几年,基于记录值模型参数的Bayes估计问题,激发了许多学者的研究热情.Bayes统计与经典统计相比,优点较多,它不仅重视总体信息和样本信息的使用,而且更加重视收集以及加工先验信息,把先验信息数量化,形成先验信息并参与统计推断,这样一来,不但结果更加精准,计算过程也会更加简单[4].
参考文献:
[1]王亮,师义民.平衡损失函数下Cox模型的可靠性分析:记录值样本情形[J].工程数学学报,2011,28(6):787-793.
[2]林正炎,陆传荣,苏中根.概率极限理论基础[M].北京:高等教育出版社,1999:80-85.
[3]Arnold B C, Villasennor J A.The asymptotic distributions of sums of records[J].Kluwer Academic Publishers, Extremes,1998,1(3):351-363.
[4]徐宝,王德辉,付志慧.一类对称损失下刻度参数估计的不变性[J].吉林大学学报:理学版,2007,45(5):697-701.

