一种噪声类型识别的遥感图像PDE去噪模型
张洪为,孙玮琪
(1.通化师范学院 数学学院,吉林 通化 134002;2通化师范学院 历史地理学院,吉林 通化 134002)
1 引言
遥感图像的分析、识别是遥感技术领域的重要内容.然而遥感图像在获取和传输的过程中通常因噪声的干扰而引起质量下降,影响了图像的视觉效果和进一步分析识别,因此必须对其进行降噪处理.如何在去除图像噪声的同时保持图像的边缘是研究者们一直追求的目标.
偏微分方程去噪方法由于其良好的去噪特性和模型建立的灵活性而受越来越多的研究者关注[1-3].Perona和Malik率先提出了著名的非线性扩散模型[4](简称P-M模型),该模型将图像去噪和边缘检测很好的统一在一起,不仅能有效的去除图像噪声,而且还能锐化图像的边缘.然而随后研究发现,该模型具有“病态”特性和对于强边缘附近噪声的无效性[5-6].随后研究者们针对P-M模型的不足提出了许多改进的模型[6~9],虽然这些模型在一定程度上缓解了P-M模型的不足,在去除图像噪声方面都取得了一定的效果,然而它们在对图像去噪之前都没有考虑噪声的类型以及噪声的强弱,这样势必会使图像去噪变得盲目.
本文首先通过小波变换对含噪遥感图像的噪声类型进行判断,进一步提出自适应的偏微分方程去噪模型,该模型根据遥感图像中所含噪声类型的不同自适应的改变模型的相关参数,实验结果证明了该模型的有效性和稳定性.
2 小波域噪声类型识别
遥感图像经前期处理后所含噪声可分为两类[9]:一类可看成高斯噪声,另一类可看成椒盐噪声,遥感图像所含噪声可看成这两种噪声中的一种或是两种噪声的叠加,如何判断遥感图像中所含噪声是高斯噪声、椒盐噪声或两者的叠加是遥感图像滤波的关键问题.由于图像经小波变换后能量主要集中在大尺度的子带上,而小尺度的高频子带系数较小、能量较低.因此小波变换为分析图像的噪声类型提供了一种较好的方法.图像经过一层小波变换后分解为4个子图像,包括低频分量图LL和3个方向(水平、垂直、斜线)的高频分量图HL、LH、HH.研究发现,图像经过小波变换后高频子带的HH系数不仅能反映出图像受干扰噪声的大小,而且能反映出图像受干扰噪声的类型[10].根据上述特点,可对图像噪声类型进行识别,具体如下:
设HH系数矩阵为{D(l,h)(l,h=1,2,…,N/2)},按系数幅值(绝对值)的大小可将不显著的系数提出:
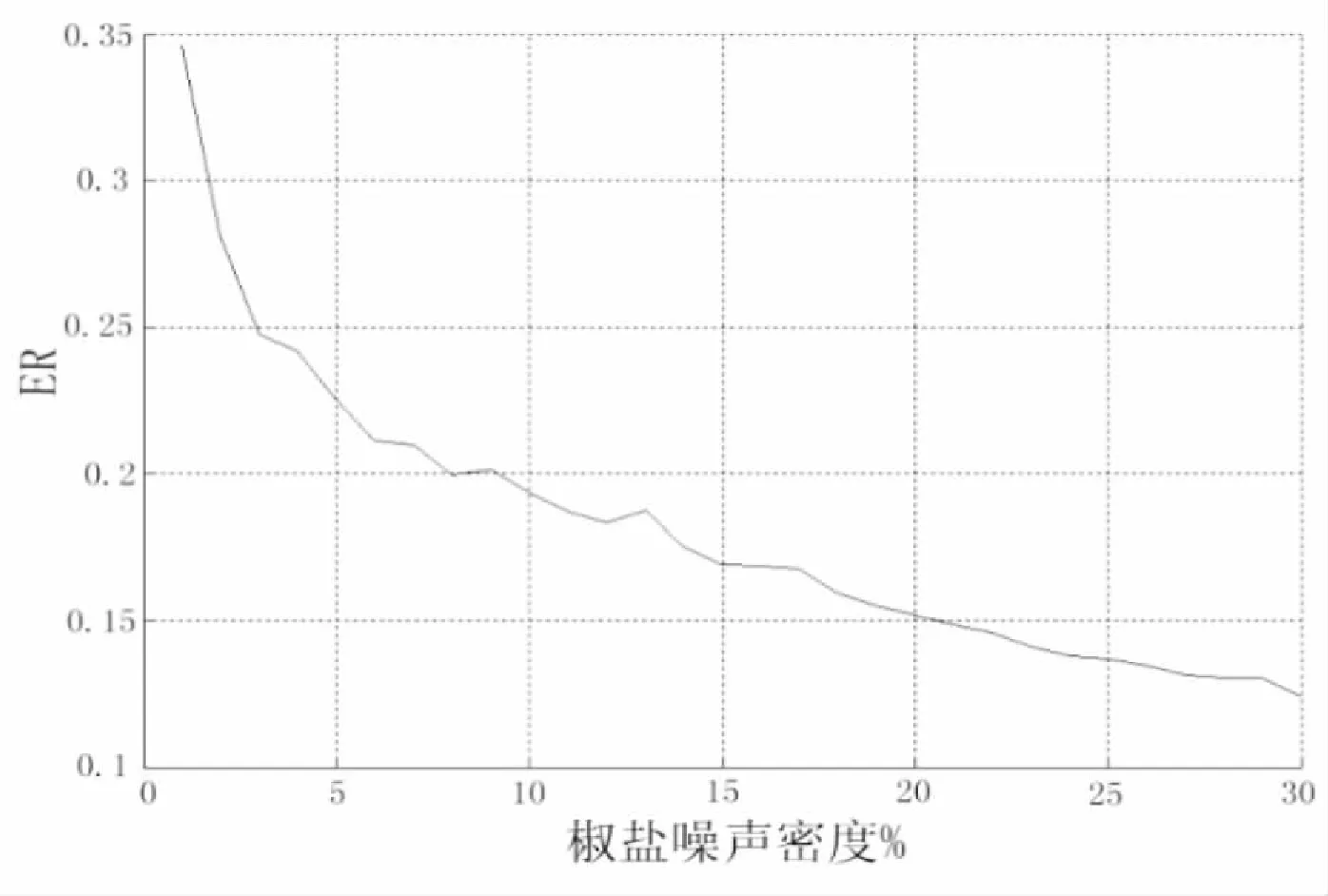
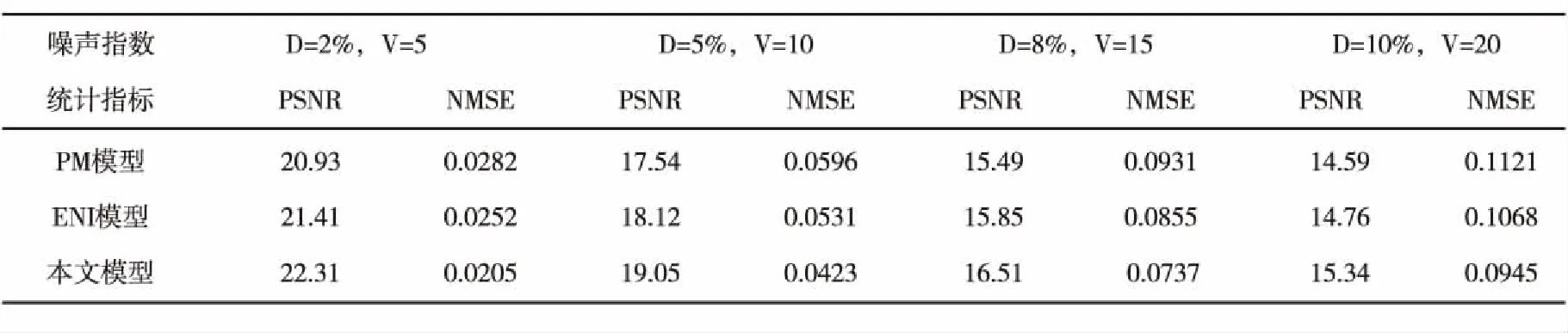
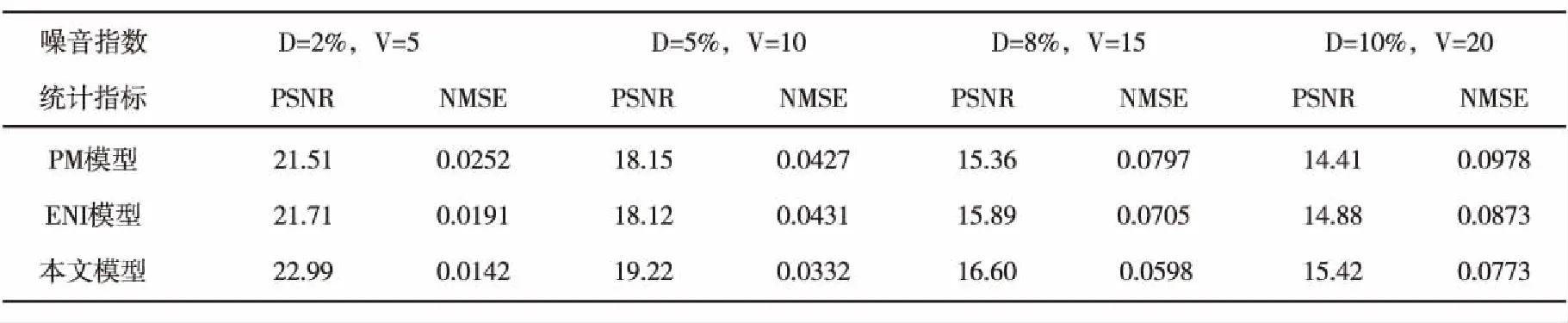
DT(l,h)={D(l,h),|D(l,h)| (1) 其中,T为确定系数是否显著的阀值.进一步定义不显著系数的能量与系数总能量的比为 (2) 式中num为总的HH系数个数,而numT为满足(1)式的系数个数. 为了能够根据ER值识别图像中的噪声是高斯噪声还是椒盐噪声,选取大小为256×256的lena灰度图像,依次加入方差为1~30的高斯噪声,并对加入不同噪声的图像进行小波变换,根据文献[10],选取T=50作为度量小波系数是否显著的阀值,计算出不同噪声图像的ER值,得到高斯噪声方差和 的关系曲线如图1所示.类似地,在lena图像中依次加入密度为1%~30%的椒盐噪声利用同样的方法,可得椒盐噪声密度与ER的关系曲线如图2所示. 图1 高斯噪声方差与ER关系图 图2 椒盐噪声密度(%)与ER关系图 从图1中可以发现,图像的ER值随着高斯噪声方差的增大而先增大后减小,一般当高斯噪声方差小于30时,ER>0.6 .由图2可以发现,图像的 值随着椒盐噪声密度的增大而减小,一般当椒盐噪声密度大于1%时,ER<0.4.因此,在通常情况下,若图像中仅含有某种单一噪声,当ER>0.6时可认为图像中含有高斯噪声,当ER<0.4时可认为图像中含有椒盐噪声.若图像中同时含有高斯噪声和椒盐噪声,则当ER>0.6时,认为图像噪声以高斯噪声为主,对图像去噪时作为高斯噪声处理,当ER<0.4时,认为图像噪声以椒盐噪声为主,对图像去噪时作为椒盐噪声处理,若0.4≤ER≤0.6时认为图像所含两种噪声强度相当,对图像去噪时作为混合噪声处理. 针对P-M模型难以去除椒盐噪声的不足,文献[11]提出一种基于椒盐噪声的非线性扩散模型,具体过程如下: d(p,q)=|u(p)-u(q)| (3) (4) 最后将像素点p的ENI定义为 (5) 1)对于椒盐等脉冲噪声的ENI是最小的,接近于零,因为脉冲噪声的灰度强度与其周围像素的灰度强度相比是比较突出的.2)对于图像边缘上的像素点ENI大小处于中间水平,接近于N/2.3)对于图像内部平坦区域像素点ENI是最大的,接近于N. 基于上述几点,定义扩散函数为 (6) 用该扩散函数代替P-M模型中的扩散函数就得到相应的基于ENI的非线性扩散模型(后文简称ENI模型) (7) 理论和实验均表明,ENI模型对于椒盐等脉冲噪声有较好的去噪效果,但对于高斯噪声去噪效果不够理想,因为文中所定义的区分图像噪声、边缘和内部平坦区域的ENI只针对噪声点灰度值与其邻域的像素值差别较大且孤立分布的椒盐等脉冲噪声才有效,而对附加在整幅图像上的高斯白噪声无法区分.所以利用ENI模型对含有高斯噪声或含高斯与椒盐混合噪声的遥感图像进行去噪,效果显然是不理想的. 为了对含噪声遥感图像去噪之前,充分的考虑其所含噪声的类型,而不至于盲目的进行去噪,本文根据小波变换所得对角高频子带不显著系数与系数总能量比 能够区分高斯与椒盐噪声的特性,以及P-M模型对高斯噪声具有较好的去噪效果且能加强保持图像的边缘,但对椒盐噪声去除效果差,而 模型去除椒盐噪声效果较好,但对高斯噪声去噪效果较差的特点,进而提出如下的去噪模型: (8) 其中,η∈[0,1]为权函数,这里将其定义为 (9) u0(x,y)为观测图,u(x,y,t)为时间尺度t下u0(x,y)的平滑版本. (10) 其中 (11) (12) 所提出模型的数值解算法步骤如下: Step1.初始化:选取大小为m×n的含噪图像ln,记u0=In,取收敛精度为p. Step2.循环计算:k=0,执行如下过程: Step2.1首先对含噪图像In做小波变换,得对角高频子带HH系数. Step2.2按照式(2)计算k时刻ERk的值 Step2.3当K=1时刻,利用式(9)计算权函数 Step2.4按照式(10)计算k+1时刻的图像uk+1 Step2.5若|uk+1-uk|>p,置k=k+1,返回执行Step2.1,否则执行Step3. Step3结束. 为了验证本文方法的有效性,选取了大小为256×256的两幅遥感图像作为测试图像,在多种强度的高斯和椒盐噪声的混合噪声下,将所提出的模型与P-M模型和ENI模型进行了比较.客观评价指标采用如下的峰值信噪比(PSNR)和归一化均方差(NMSE). 式中:u*(i,j)是算法去噪后的图像;u0(i,j)是标准的不含噪声图像;m和n分别是图像的长和宽. 表1~2是利MATLAB分别对遥感图像A和B添加不同强度的高斯和椒盐的混噪声利用P-M模型、ENI模型和本文模型去噪后的效果图,其中V表示高斯噪声方差,D表示椒盐噪声密度. 从表1~2可以看出,采用P-M模型去噪后的图像,尽管高斯噪声已基本去除,但表面却残留着难以去除的椒盐噪声,采用ENI模型去噪后的图像则正好相反,图像表面的椒盐噪声去除较为彻底,但却残留着难以去除的高斯噪声,而采用本文提出的模型,不仅很好的去除了高斯和椒盐噪声,而且保持了原图像中的大量细节和边缘信息. 进一步对上述三种方法去噪结果进行峰值信噪比和归一化方差统计,如表3~4所示,其中V表示高斯噪声方差,D表示椒盐噪声密度.从统计数据可以看出,对于不同的遥感测试图像和不同强度的混合噪声,本文模型与P-M模型、ENI模型相比具有更高的峰值信噪比和归一化方差,即本文模型的客观效果更好,且具有较好的稳定性. 表1三种模型去除图像A中不同强度的高斯与椒盐混合噪声效果图 表2 三种模型去除图像B中不同强度的高斯与椒盐混合噪声效果图 表3 三种模型去除图像A中不同强度的混合噪声所得结果的PSNR和NMSE统计 表4 三种模型去除图像B中不同强度的混合噪声所得结果的PSNR和NMSE统计 本文根据小波变换能够对噪声类型进行识别的特点,以及P-M模型和ENI模型各自对高斯与椒盐噪声去噪的优点和不足,提出一种基于噪声类型识别的PDE去噪模型,该模型能够自动判断遥感图像所含噪声的类型而自适应的进行去噪,在有效去除图像噪声的同时能够很好的保持了图像的边缘和纹理信息. 参考文献: [1]崔丽娜,潘振宽,魏伟波,石洁,耿秀秀.基于PM模型的曲面去噪变分水平集方法[J].中国图象图形学报,2010,15(3):361-366. [2]马少贤,江成顺.基于四阶偏微分方程的盲图像恢复模型[J].中国图象图形学报,2010,15(1):26-30. [3]Y.Shi*,C.Rei,H.Wang.A novel PDE based image restor-ation:Convection-diffusion equation for image denoising[J]. Journal of Computational and Applied Mathematics,2009,231(2):771-779. [4]Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Trans on Pattern Anal Machine Intell,1990,12(7):629-639. [5] Catte F,Lion P L,Morel J M,Coll T..Image Selective Smoothing and Edge Detection by Nonlinear Diffusion[J].SIAM Journal on Numerical Analysis,1992,29:182-193. [6]祝轩,周明全,朱春香,耿国华,王大凯. 曲率驱动与边缘停止相结合的非线性扩散及其在图像去噪中的应用[J].光子学报,2008,37(3):609-612. [7]Alvarezl, Lions P L, Morel J M.Image selective smoothing and edge detection by nonlinear diffusion II[J].SIAM J Num Anal,1992,29(3):182-193. [8]Yu-Li You , Kaveh M. Fourth-Order Partial Differential Equations for Noise Removal[J].IEEE Trans on Image Processing,2000,9(10):1723-1729. [9]王相海,张洪为,李放.遥感图像高斯与椒盐噪声的PDE混合去噪模型研究[J].测绘学报,2010,39(3):283-294. [10]张旗,梁德群,樊鑫,李文举.基于小波域的图像噪声类型识别与估计[J].红外与毫米波学报,2004,23(4):281-285. [11]Jian Wu and Chen Tang.PDE-Based Random-Valued Impulse Noise Removal Based on New Class of Controlling Functions[J].IEEE Trans on Image Processing,2011,P P(99):1-10.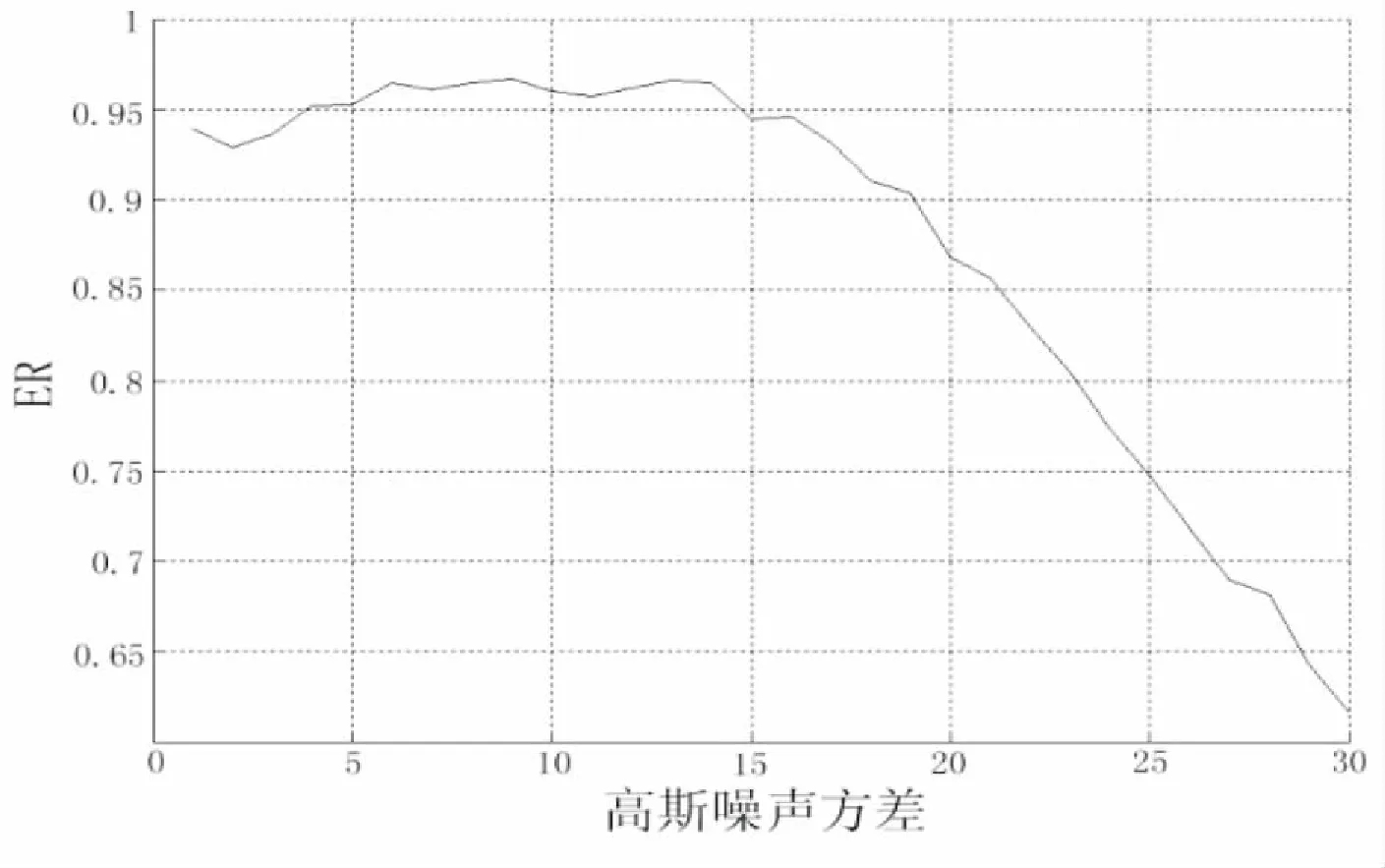
3 基于ENI的去噪模型
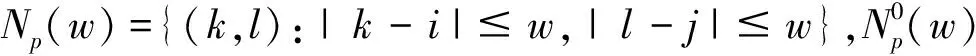
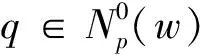
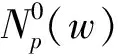
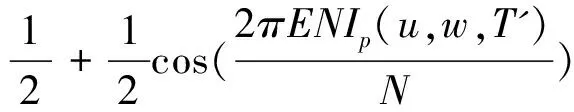
4 一种噪声类型识别的PDE去噪模型
4.1 新模型的提出
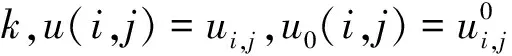
4.2 模型分析
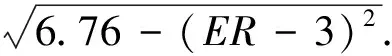
4.3 模型的算法实现
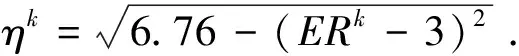
5 实验与讨论
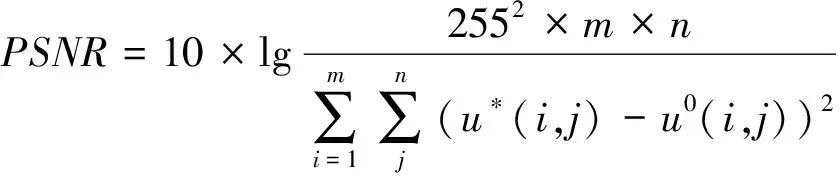


6 结论

