SPSS软件在电量需求预测中的应用

杜玉霞,梁 武,俞亭亭

(宿州学院 数学与统计学院,安徽 宿州 234000)

SPSS[1-2]统计软件是使用最为普遍的统计软件之一，它是由数据录入、资料编辑、数据管理、统计分析、报表制作、图形绘作为一个整体，具有强大的数据管理和分析功能，支持多种统计图表的结果输出.目前，SPSS广泛应用于特定区域的销售分析、市场营销、统计、社会经济调查、企业管理、教学和行政管理等领域. 本文运用SPSS软件对西北电网电量需求进行外推预测，取得了较高的预测精度.

1 时间序列ARIMA(p,d,q)模型

ARIMA(Autoregressive Integrated Moving Average)模型全称差分自回归移动平均模型，是由博克斯(BOX)和詹金斯(Jenkins)于20世纪70年代初提出的一种著名的时间序列预测方法，又称为B-J模型.它的一般形式为：ARIMA(p,d,0)，其中p是自回归模型的阶数，d为时间序列成为平稳时所做的差分次数，q是移动平均的阶数.ARIMA方法能够在对数据模式未知的情况下找到适合数据所考察的模型，在医学等很多方面得到了广泛应用[3-4].其建模思想是将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列,并从时间序列的过去值及现在值来预测未来值.通过对模型的分析与研究，能够从本质上认识时间序列的结构与特征,达到最小方差意义下的最优预测.

2 电量需求的ARIMA(p,d,0)模型

以下就2005.1-2006.12西北电网电量需求数据(见表1)，建立电量需求的ARIMA(p,d,q)模型. 绘制电量需求数据时序图(见图1).通过观察图1，可以看出数据呈现周期波动，并且存在明显的递增趋势.运行SPSS软件得到原始数据的自相关系数和自相关图，见表2、图2.

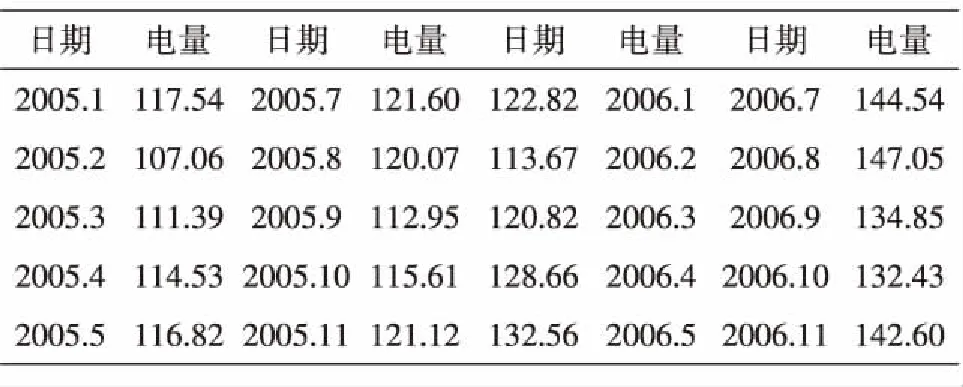
表1 2005.1-2006.12 西北电网电量需求 单位:亿千瓦时

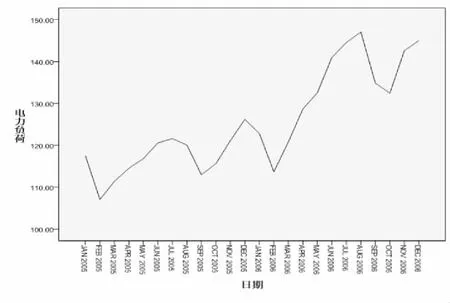
图1 2005-2006年电力负荷时间序列数据序列图

图2 自相关图

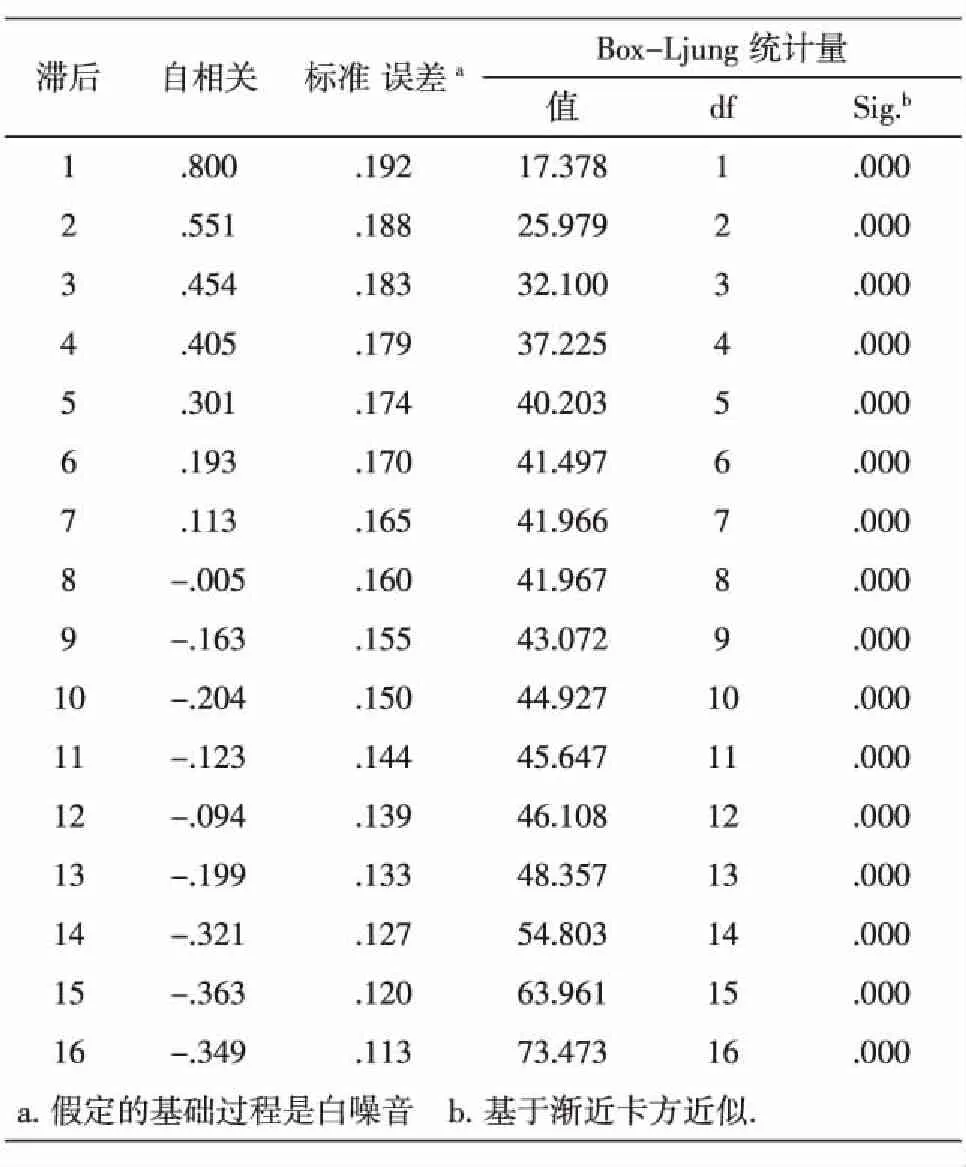
表2 自相关系数

图3 一阶差分的时序图

图4 一阶差分后自相关图

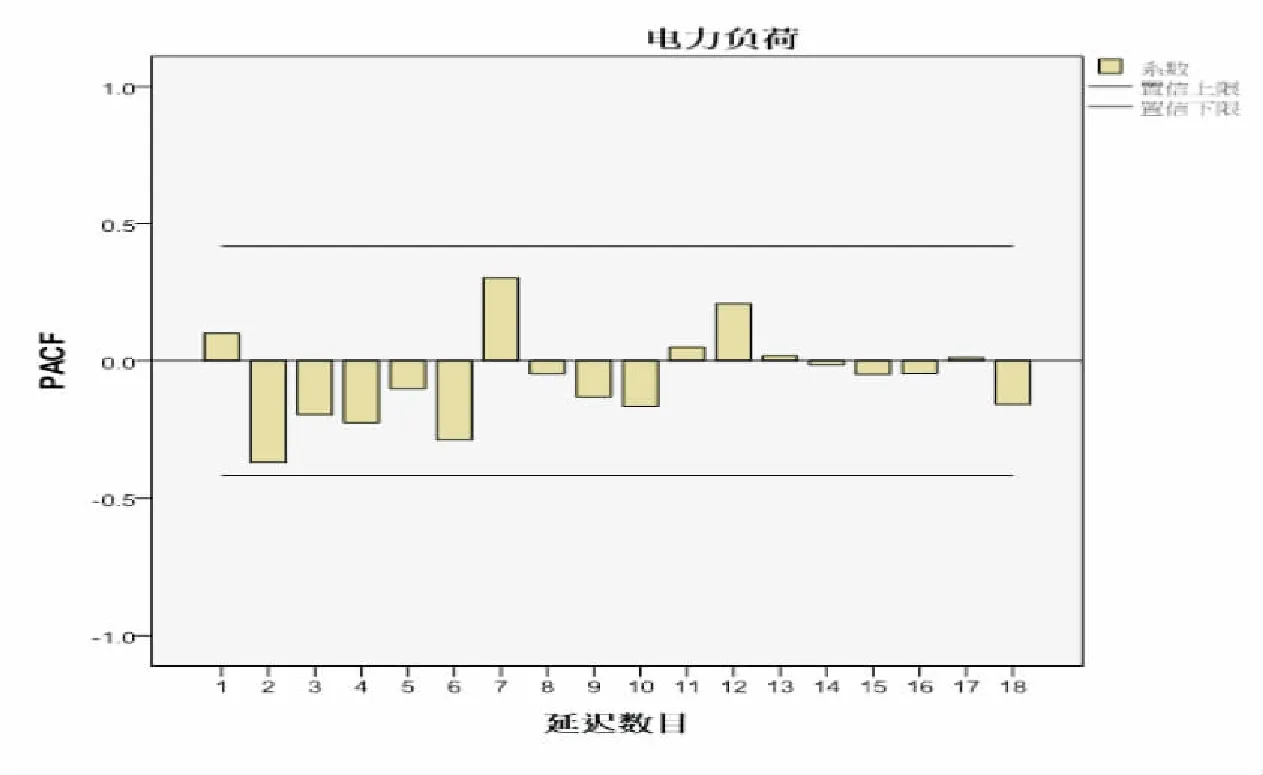
图5 一阶差分偏相关图

图6 ARIMA模型残差的相关函数图

由图2和表2可以看出该序列延迟了4阶后，相关系数衰减到接近0，然后又出现了较大的负相关.这表明该序列具有显著单调递增的趋势.所以我们需要利用差分的方法对原序列进行变换，剔除长期趋势使得序列变得平稳.进行1阶差分得时序图3,自相关图4，偏相关图5.

观察图3可以看出一阶差分后长期趋势基本上从序列中剔除，原序列变换成了平稳时间序列，差分阶数d=1,观察图4、5可以断定p=1,q=0，确定西北电网电量需求的时间序列模型为ARIMA(1,1,0).

3 对ARIMA(1,1,0)模型进行检验

对于西北电网电量需求的ARIMA(1,1,0)模型，运行SPSS软件得模型参数见表3，残差的相关函数图见图6，模型统计量见表4.

表3 ARIMA 模型参数

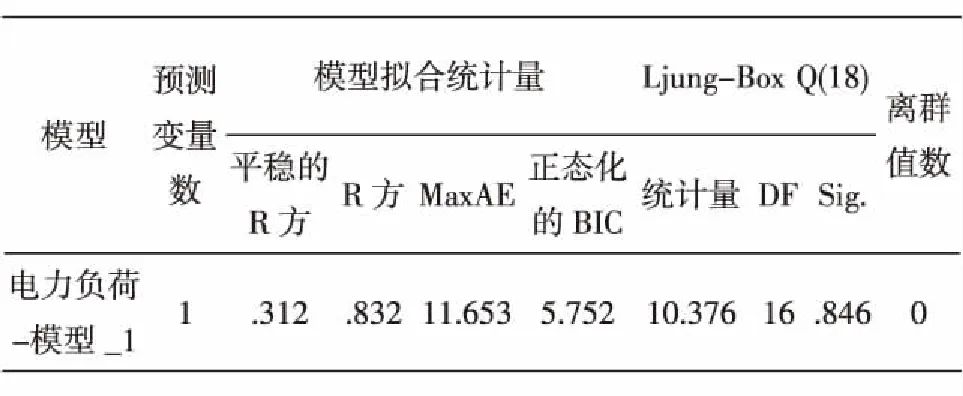
表4 模型统计量

从表3可以看出t统计量的值远小于0.05，表明此模型一阶自回归系数显著.由图6可以看出两个图形都没有显著的趋势特征(拖尾或截尾)，且残差序列的自相关和偏自相关系数大多接近于零，这表明残差序列已经达到白噪声，模型与数据拟合的较好.

由表4模型统计量中R方上来看，拟合优度也达到了0.832，sig值为0.846远大于0.05，这说明了构建的ARIMA(1,1,0)模型的拟合效果良好，可以用来预测西北电网电量.

图7 预测的拟合结果

4 运用ARIMA(1,1,0)模型进行预测

运行SPSS软件，得拟合结果见图7，从图7预测的拟合曲线图可以直观的看出ARIMA(1,1,0)模型很好的拟合了原序列.运用该模型进行外推预测得2007.1-2007.3的预测结果见表5.

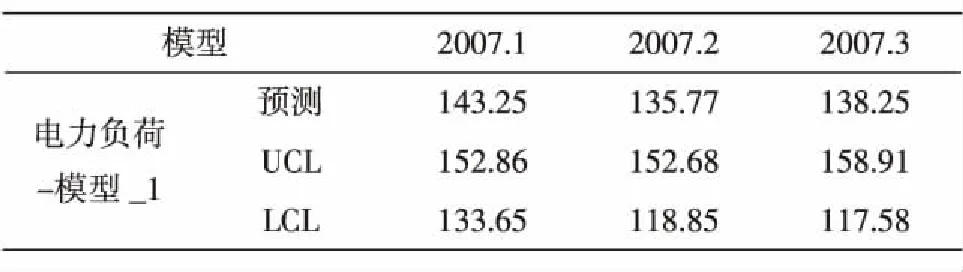
表5 预测结果

5 结语

参考文献：

[1]郭志刚.社会统计分析方法—SPSS软件应用[M].北京:中国人民大学出版社,1999.

[2]李志辉,罗平.SPSS for Windows统计分析教程[M].北京:电子工业出版社,2006.

[3]周水森.ARIMA模型在疟疾发病预测中的应用[J].中国原生物学杂志,2007,2(4):284-286.

[4]吴家兵,叶临湘,尤尔科.ARIMA模型在传染病发病率预测中的应用[J].数理医药学杂志,2007,20(1):90-92.