基于椭圆运动方式的小工具抛光去除函数
刘猛猛,洪 鹰
(天津大学机械工程学院,天津300072)
基于椭圆运动方式的小工具抛光去除函数
刘猛猛,洪 鹰*
(天津大学机械工程学院,天津300072)
为了改进传统的小工具抛光的去除函数的特性和提高去除效率,在行星和平转动抛光方式的基础上,通过三转子机构,实现了椭圆式运动方式;以Preston理论为基础,研究并推导了在这种运动方式下的材料去除函数;通过计算机模拟得到了去除函数的面形矩阵,经过优化后获得了最终的抛光参量,得到了与理想的高斯型函数吻合程度高的去除函数。结果表明,仿真加工后,其去除效率优于行星式去除函数。基于椭圆运动方式的小工具抛光避免了行星和平转动抛光方式去除函数存在的缺陷,有助于提高抛光过程的去除效率。
光学制造;去除函数;椭圆运动;仿真加工
引 言
随着激光技术的发展,对高精度大口径光学元件需求不断加大[1]。计算机控制表面成型技术在高精度光学元件,特别是大口径元件的实际加工中得到了广泛的应用,而小工具抛光正是其典型代表。目前,小工具抛光的运动方式主要有两种:行星运动式和平转动式。其去除函数与理想的高斯型去除函数相比,存在一定的缺陷:去除函数中心不是单一峰值,甚至出现凹陷,有可能使工件表面出现凸起;曲面不光滑,会造成中高频误差;曲线边缘处曲线斜率过于陡峭。而这些缺陷难以通过调整其运动参量而加以改善,以至于小工具抛光技术在光学元件加工领域的应用受限,发展缓慢。通过改变抛光盘的形状是改善这种现状的一种方式[2],但受限于加工条件,难以获得与理论形状完全一致的抛光盘;同时在抛光盘直径相同的前提下,减小其有效抛光面积,可以降低去除的效率。因此改变其运动方式,是一种改善去除函数特性的有效方法。
作者基于行星运动方式的相关理论,在自转与公转之间增加1级椭圆运动,形成三转子抛光机构,并对其各个运动参量进行优化,获得了理想的去除函数。
1 去除函数
1.1 行星运动式抛光技术相关理论
去除函数的理论基础是Preston方程[3],材料的去除量与抛光盘、工件间的压力、速率成正比:

式中,z为某一点的材料去除量;t为时间;K为比例常数,它由除速度和压力以外的其它因素决定;v为某点某一瞬时的速率;p为该点该瞬时的压力。则对于抛光面上任一点其去除函数为:
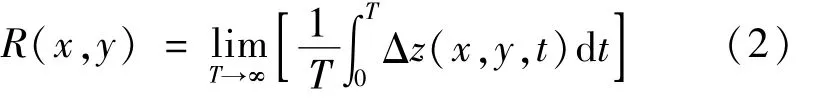
式中,R(x,y)为去除函数;T为抛光盘在任意一个给定区域所停留的时间;Δz(x,y,t)为不移动抛光模的材料去除量,是抛光模坐标和时间的函数。
行星式运动机构如图1所示。抛光盘的公转电机角速度为ω1,自转电机角速度为ω2,偏心距为e,R为抛光盘半径,对于抛光区域内一点,与公转中心距离为s,夹角为θ,ω1=dθ/d t。令g=s/R,ρ=e/R,n=ω2/ω1,则随距离s变化的去除函数为[4]:
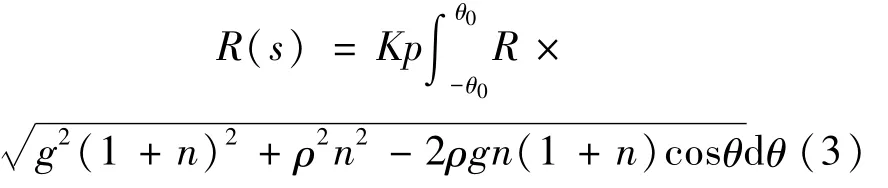

Fig.1 Schematic diagram of planetmotion model
适当选取运动参量,经过优化后[5],其归一化特性曲线如图2所示。
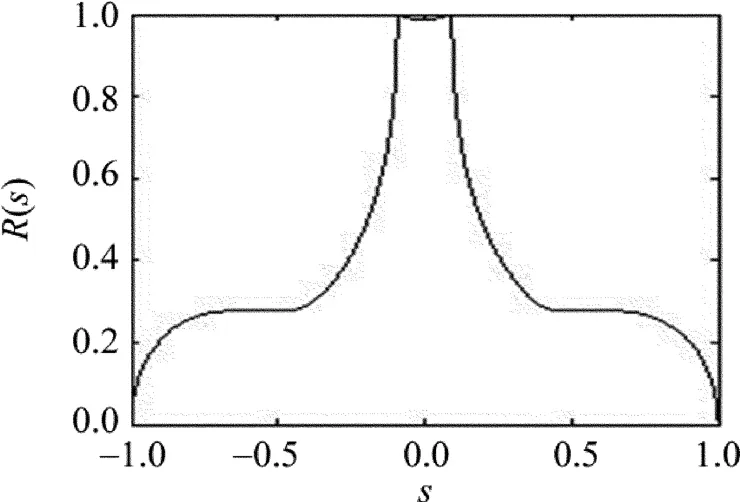
Fig.2 Performance curve of polishing pad(ρ=0.83,n=8)
1.2 椭圆运动式去除函数
在传统的行星式运动方式的自转与公转之间增加正弦连杆机构以及十字滑块,以实现椭圆运动方式,其机构简图如图3所示。
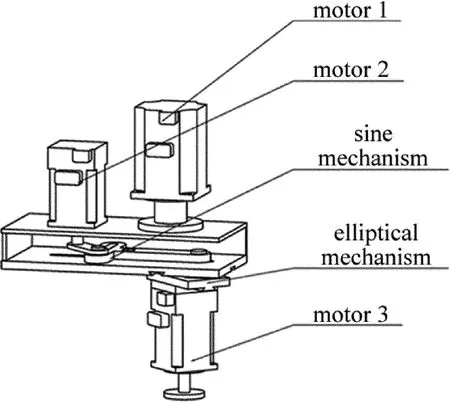
Fig.3 Sketch map ofmechanism
建立简化后的数学模型,如图4所示。O为公转中心;O1A为曲柄,长度为r;椭圆电机做逆时针回转运动,角速度为ω3,转角为θ1;AB为滑竿,长度为l1;BC为椭圆摆杆,长度与r相等,与x轴夹角为θ2,其上的M点做椭圆运动,是自转中心,与C点的距离为d。

Fig.4 Schematic diagram of ellipsemotion model
此时M点沿坐标轴方向的速度分量vx′,vy′为:

考虑公转运动后,其速度分量vMx,vMy为:
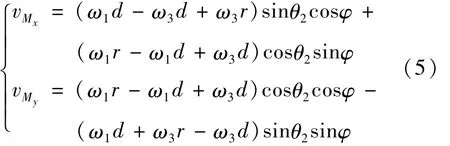
式中,φ为公转运动的转角,对于抛光盘上任意一点Q(x,y),在任意时刻的沿坐标轴的速度分量vQx,vQy为:
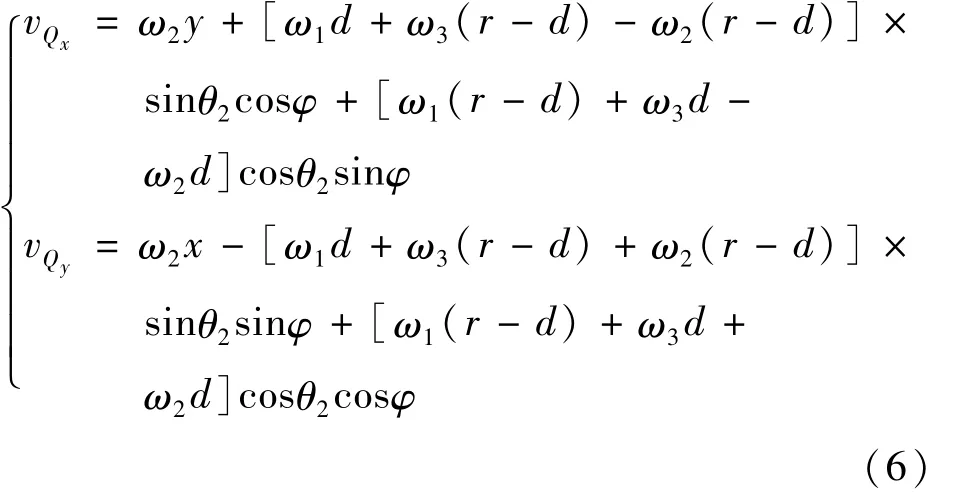
则Q点速度大小为:
当抛光盘在Q点存在材料去除时,应满足(xM-x)2+(yM-y)2≤R2,即:
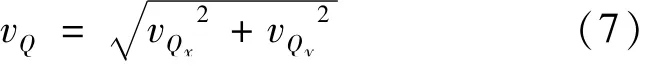
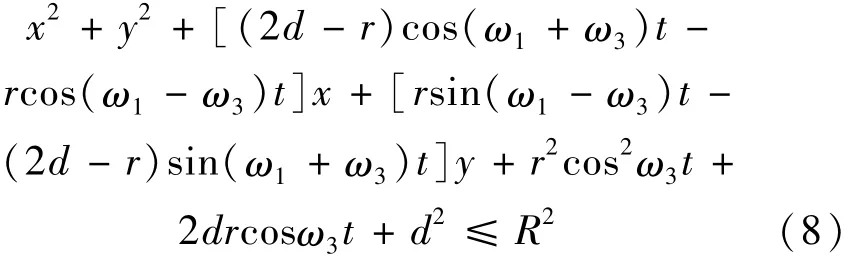
根据上式可以确定有效的时间区间t1,t2,…,tn∈T,则Q点处归一化去除函数为:

2 参量优化
基于椭圆运动方式的去除函数,当各个参量取值不同时差别较大,需要对各个参量进行优化。对于给定的曲柄转速以及长度,决定去除函数的参量分别是公转电机角速度ω1,自转电机角速度ω2,点M与点C的距离d以及抛光盘的半径R。适当选取各个参量的取值,获得较为理想的去除函数形状,归一化处理后作为优化程序的初始值,如图5所示。
理想的去除函数应满足以下特点[6-7]:(1)具有旋转对称特性;(2)在中心处具有单个峰值,而边缘处去除量为0;(3)中心处和边缘处斜率为0;(4)连续光滑。
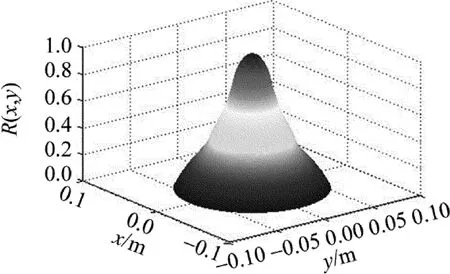
Fig.5 Initial value of removal function
参量优化以上述原则为优化条件,对参量进行优化。
由于运动方式基于椭圆运动,因此公转与椭圆运动的周期比决定了其表面的起伏特性。依据旋转对称的原则,对去除函数同一半径上函数值的均方差为目标进行优化,确定最佳转速比。给定适当的取值范围后进行1维搜索优化。优化后的公转角速度与椭圆运动角速度的比值为1∶0.073,均方差由初始的0.0076减小到0.0029。
假设理想函数为以四次多项式曲线为母线旋转后得到的曲面[8]。根据上述原则确定出边界条件,化简后可以得到包含一个参量的曲线方程,并将其与上一步的去除函数进行拟合,可以得出与上述结果最为接近的理想去除函数。得到的四次多项式曲线为:

以理想函数为逼近目标,以均方差为优化对象,对自转速度ω2、距离d和抛光盘的半径R进行优化,使去除函数逼近理想去处函数。由于可能存在许多局部最优解,优化中对3个参量分别进行1维搜索,选择其中最敏感的参量替代初值继续下一步优化,当满足给定的精度要求后则停止。优化后公转角速度与自转角速度的比值为1∶5.1691,距离d与曲柄长度的比值为1∶0.1870,抛光盘半径与曲柄长度的比值为1∶0.4979,均方差由0.029变为0.028。并再次对公转速度优化,检验对其的影响大小,优化后的其均方差仍为0.028,影响极小,可将上述优化结果视为最终结果,如表1所示。其去除函数如图6所示,计算流程图如图7所示。

Table 1 Optimized parameters

Fig.6 Final value of removal function
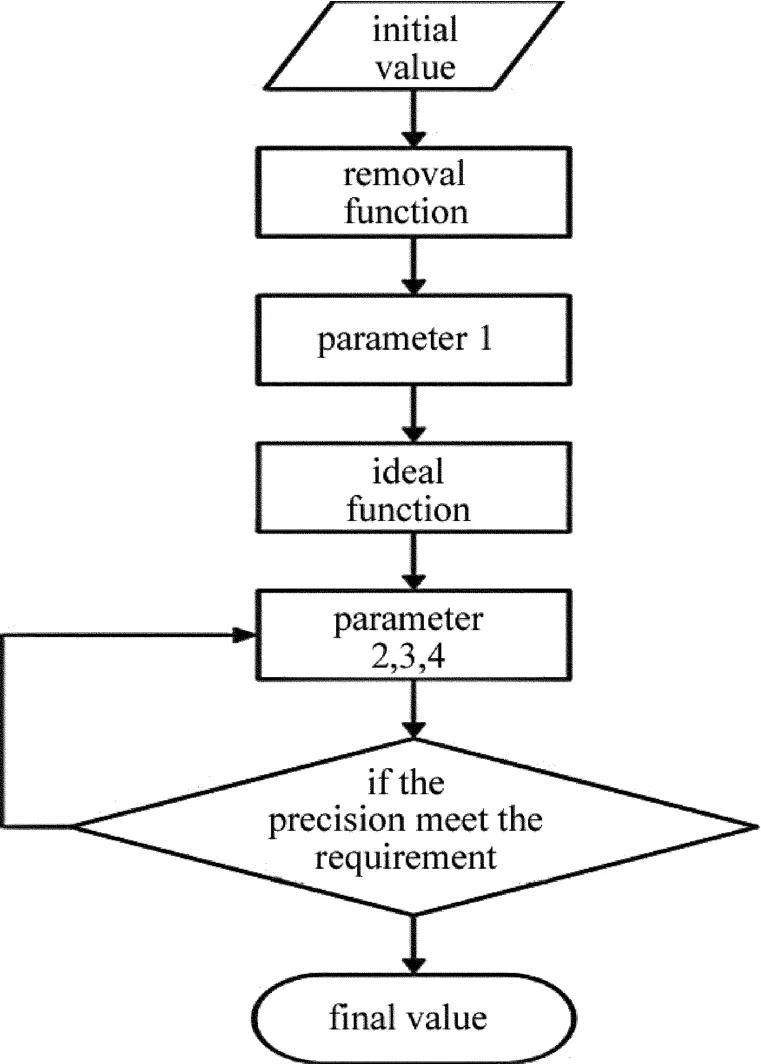
Fig.7 Flow chart
选用正弦面形误差作为初始面形误差H(x,y),幅值为2。
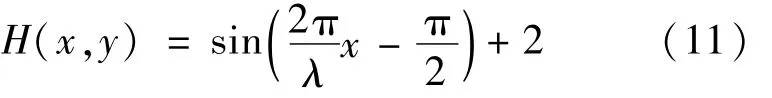
式中,λ为正弦频率参量,取λ=2.5;x,y=[-5,5]。
分别采用椭圆式以及行星式去除函数进行仿真加工,以相同的参量通过脉冲迭代法计算驻留时间[9-11]。图8为仿真加工结果。两种去除函数均归一化处理,经过20次迭代后,其面形误差分别如图8b和图8c所示。
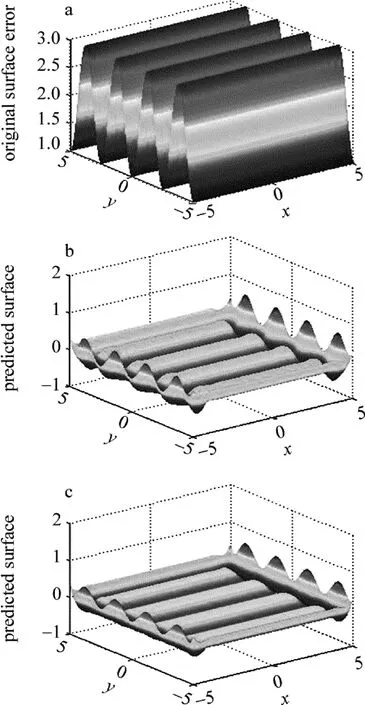
Fig.8 Result of simulated processa—sine surface error b—result of planetmotion c—result of ellipse motion
经过行星式运动的抛光去除函数仿真加工后,面形误差均方根值(rootmean square,RMS)值由初始的2.1205减小为0.3184,其峰谷(peak-to-valley,PV)值由3降为0.5833;而椭圆式运动的抛光函数经仿真加工后,面形误差的RMS值减小为0.1308,PV值减小为0.5525。不考虑边缘效应,从RMS值的变化结果可以看出,基于椭圆方式的去除函数在加工时的收敛效率更高。
3 结 论
对传统的行星式抛光技术进行了理论创新,通过三级转动实现了基于椭圆运动方式的小工具抛光,并且获得了较为理想的去除函数。与行星式运动的去除函数相比,去除函数更加光滑,没有突变,更加接近理想的高斯型去除函数。
[1] LÜBD.Some recentadvances in high-power solid-state lasersand related technologies[J].Laser Technology,1998,22(4):193-198(in Chinese).
[2] CHEN H N,WANG JL,LIX L,etal.Modeling and approximation of Gaussian-like removal function in dual-rotor polishing technology of optics elements[J].Acta Photonica Sinica,2013,42(3):1-6(in Chinese).
[3] XIN Q M,SUN Y N,XIE J H.Modern optical manufacturing technique[M].Beijing:National Defense Industry Press,1997:8-14(in Chinese).
[4] WANGQD,LIU M C,ZHANGH X.Removing function of polishing pad in computer controlled optical polishing[J].Optical Technique,2000,26(1):32-34(in Chinese).
[5] WANG Q D,YU JCh,ZHANG F.Polishing performance comparison of small polishing pad worked in differentmotion model in computer controlled optical polishing[J].Optics and Precision Engineering,1999,7(5):73-79(in Chinese).
[6] SHANGW J.Model building and simulation of computer control deterministic grinding and polishing[D].Changsha:National U-niversity of Defense Technology,2005:8-10(in Chinese).
[7] WENZEL D J,MCFALLSD S.An optimalmaterial removal strategy for automated repair of aircraft canopies[C]//Robotics and Automation,1989.Scottsdale,Arizona,USA:IEEE,1989:370-376.
[8] LIAM.Study on removing characteristics and technology of polishing of a small tool in computer control[D].Changsha:National University of Defense Technology,2003:16-26(in Chinese).
[9] ZHOU X Sh.Study on techniques in computer-controlled grinding and polishing for large andmedium aspheric surfaces[D].Changsha:National University of Defense Technology,2007:43-60(in Chinese).
[10] LUO L L,HE JG,WANG Y J,etal.Large-scale dwell time algorithm for computer controlled optical surfacing[J].High Power Laser and Particle Beams,2011,23(12):3208-3212(in Chinese).
[11] SHIF,DAIY F,PENG X Q,etal.Dwell time algorithm based on vector for MRF process of optics[J].Journal of National University of Defense Technology,2009,31(2):103-106(in Chinese).
Removal function of small tool polish based on ellipsemotion
LIU Mengmeng,HONG Ying
(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)
In order to improve the property and the efficiency of traditional removal function of small tool polish,ellipse motion method was achieved through three-rotor movement on the basis of planetmotion.Then,a new removal function was investigated and deduced based on the assumption of Preston.At last,the surfacematrix of removal function was calculated by computer and after optimization.The final parameters and the removal function which was close to the ideal Gaussian function were obtained.The results show the removal efficiency of ellipse motion is better than planetary removal’s.Removal function based on ellipsemotion can avoid the defectof previous function of planetmotion and increase the removal efficiency during polishing process.
optical fabrication;removal function;ellipsemotion;simulated process
O439
A
10.7510/jgjs.issn.1001-3806.2014.03.027
1001-3806(2014)03-0406-05
国家科技重大专项课题资助项目(2013ZX04006-207)
刘猛猛(1989-),男,硕士研究生,现在主要从事小工具抛光系统的开发研究。
*通讯联系人。E-mail:hying1122@126.com
2013-07-31;
2013-08-18

