三角平衡轮廓轮胎滚动阻力的仿真研究

唐 霞，贺建芸，薛梓晨，徐海港，焦志伟*

(1.北京化工大学 机电工程学院，北京 100029；2.山东时风(集团)有限责任公司，山东 高唐 252800)

汽车安全、节能、环保已成为当今汽车工业发展的主题，这要求与之匹配的轮胎性能相应提高。汽车轮胎是由橡胶及橡胶基复合材料构成的，它是集材料、几何、边界接触非线性以及热状态于一体的复杂结构体，轮胎力学场与温度场的分析十分复杂[1]。轮胎的滚动阻力分析以力学分析为基础，滚动阻力又是轮胎温度场分析的基础。轮胎的滚动阻力由车辆技术状况如路面参数、轮胎结构参数和车速等因素决定。早期的轮胎滚动阻力研究以实验为主，主要有滑行法、反拖法等道路实验方法或台架转鼓测试方法，但这些实验无法给出精确的分析，为了能够更为精确地分析轮胎滚动阻力，从而指导轮胎的低滚动阻力设计，有限元方法在20世纪90年代开始被引入到轮胎滚动阻力分析与开发流程中[2-3]。三角平衡轮廓是指基于低扁平率的传统轮廓轮胎轮廓为基础，通过增大轮胎自由状态下的断面水平轴到胎圈的距离、缩短着合宽度、在胎肩部与胎侧部的内轮廓处增加高强度、耐高温和耐磨损的支撑块来对轮胎轮廓结构进行优化[4]。作为新型结构轮胎的支撑块必须具有良好的力学性能和热学性能。热塑性聚酯弹性体(TPEE)又称聚酯橡胶，是一类含有聚对苯二甲酸丁二醇酯(PBT)聚酯硬段和脂肪族聚酯或聚醚软段的线型嵌段共聚物。TPEE兼具橡胶优良的弹性和热塑性塑料的易加工性，软硬度可调，设计自由，是热塑性弹性体中倍受关注的新品种[5]。但是一般的聚氨酯的导热性能差，所以要对聚氨酯改性。制备高导热的高分子材料有2种途径。第一种是制备具有良好导热结构的高分子材料，如具有共轭结构的聚乙炔、聚苯胺、聚吡咯等材料。这些材料共轭结构大，能够利用电子传递机制很好地导热。导热绝缘高分子材料制备的第二种途径是向聚合物中填充导热组分来制备高分子复合材料，通用的高导热组分是高导热的无机物，笔者选择向聚氨酯中填充碳纤维，其导热率可达0.4～0.8 W/(m·K)[6-7]。本文用ABAQUS 软件建立三角平衡轮廓轮胎和255/30R22轮胎的三维模型，对其进行以60 km/h滚动工况的力学分析，算出单元积分点的生热率，提取每个单元的体积，最后计算每一块胶料的滚动阻力及轮胎总滚动阻力。

1 滚动阻力的产生机制

橡胶和聚氨酯支撑块都是粘弹性材料，其内耗的机理也是一样的。轮胎的能量损耗是胶料滞后生热以及与地面摩擦生热导致的结果，由于应变滞后于应力，胶料在受到周期性的拉伸-回复作用时，其拉伸曲线与回复曲线并不重合(理想虎克弹性材料的拉伸-回复曲线完全重合)，而是形成一个封闭的月牙状的圈形，称之为滞后圈[8]。在轮胎的稳态滚动过程中，各部位受到应力、应变的作用，橡胶复合材料粘弹性造成的滞后损失成为能量损耗的主要原因[9]，因此本文将忽略轮胎与路面的摩擦生热只考虑材料的内耗生热。轮胎滚动过程中，胶料的应力是随时间变化的周期曲线，任何周期曲线都可以经过傅里叶变换用正弦曲线表示，材料的能量损耗和能量损耗率可以通过谐应变模式下的能量损耗模型来计算,能量损耗是转速和交变应力幅的函数[10]。滚动阻力并不是一个实际的物理量，忽略轮胎与地面的摩擦损耗，滚动阻力等于轮胎热损耗除以对应时间内滚动的距离，单位为J/m[11]，如式(1)和式(2)所示。

IW=πσpεptanδp

(1)

式中：IW为一个周期内单位体积的迟滞能量损耗，MPa；σp为应力，MPa；εp为应变；tanδp为材料损耗因子。

(2)

式中：FR为轮胎的滚动阻力，N；ELOSS为轮胎总的内耗，mJ；ΔWi为第i个单元的1周期的内耗，MPa；Vi为第i个单元的体积，mm3；Rd为轮胎自由滚动下的有效半径，mm；C为轮胎一个周期滚动的距离，mm。

2 计算流程

以周期内的能量损耗公式和滚动阻力计算公式为基础，运用ABAQUS有限元软件和二次开发子程序提取需要的变量参与运算，其计算流程如图1所示。

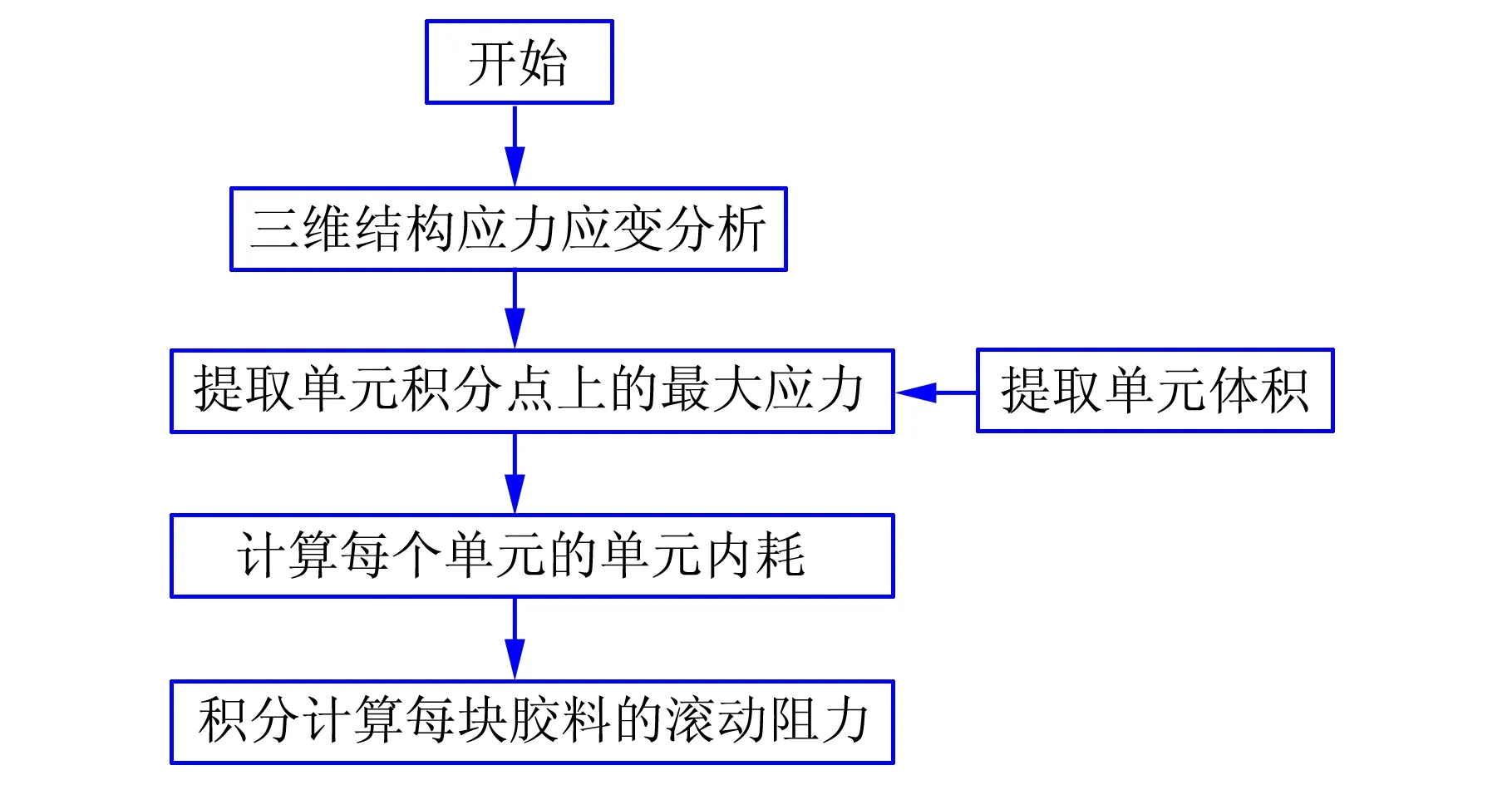
图1 计算流程图

3 轮胎有限元模型的建立

首先建立二维的三角平衡轮廓轮胎和255/30R22轮胎的轴对称模型，骨架材料包括带束层、冠带层、胎体层、胎圈。基体材料包括带束层胶、子口胶、冠带层胶、胎圈胶、内衬层、三角胶、胎侧胶、胎面胶。胶料采用YEOH模型，C10、C20、C30分别是YEOH模型的系数，骨架材料通过Embed功能嵌入对应的胶料，材料的物理参数如表1和表2[12]所示。

表1 骨架材料的物理参数

表2 胶料的物理参数

三角支撑块采用线弹性参数，杨氏模量为501 MPa，泊松比为0.38。二维轴对称模型通过SYMMETRIC MODEL GENERATION 功能建立三维模型。施加垂直载荷6 800 N，摩擦因数设为0.5，充气压力为0.29 MPa，滚动速度为60 km/h。力学分析所用的模型单元类型为C3D8H和C3D6H。不同轮廓轮胎的二维断面网格如图2所示，三维有限元模型如图3所示。

(a) 三角平衡轮廓轮胎

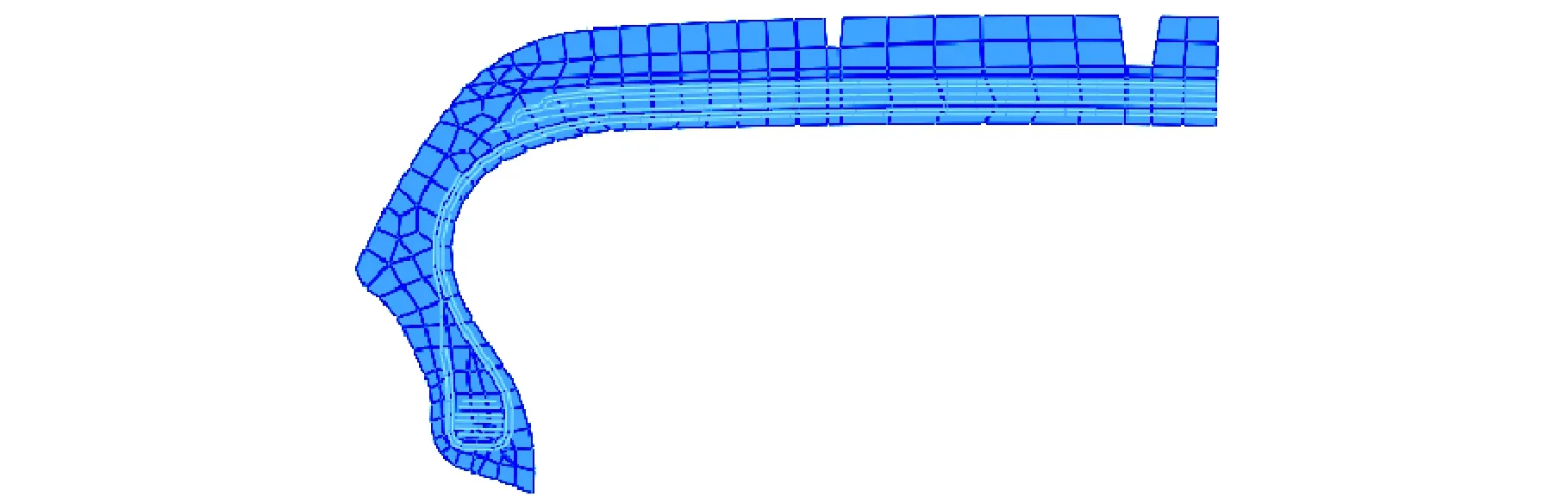
(b) 传统轮廓轮胎

图3 三维有限元模型

4 结果与讨论

2种轮胎的滚动阻力计算数据如表3所示。

表3 2种轮胎的滚动阻力计算数据

由表3可知，三角平衡轮廓轮胎的滚动阻力仅18.7N，低于255/30R22轮胎滚动阻力的二分之一。

图4为不同轮胎的损耗柱状图。

(a) 255/30R22轮胎损耗

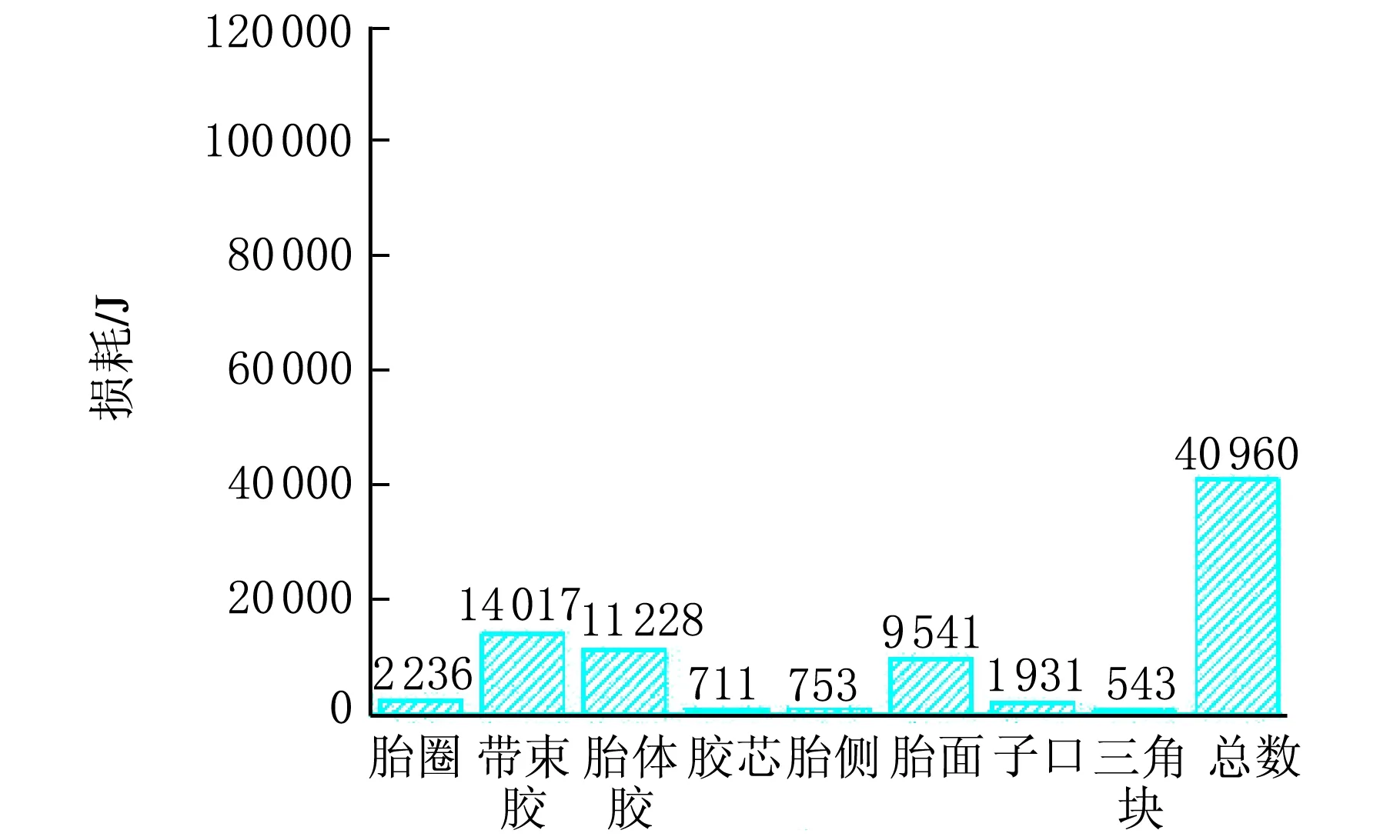
(b) 三角平衡轮廓轮胎损耗

由图4可知，2种轮胎的胎圈、胎体胶、胶芯和子口的能量损耗相差不大，数值变化最大的是胎面胶。三角平衡轮廓轮胎胎面的内耗只有255/30R22轮胎胎面内耗的五分之一，这是因为在支撑块的绷紧作用下，三角平衡轮廓轮胎的胎面在滚动的过程中被拉伸，实现真圆度的逼近和翻转力臂的减小，达到降低轮胎滚动阻力的目的[13]。其次支撑块提高了胎侧的刚度，使胎侧变形减小，所以三角平衡轮廓轮胎的胎侧内耗也显著下降。三角平衡轮廓轮胎中唯一能量损耗增大的部位是带束层胶，支撑块紧贴着轮胎内表面靠近胎肩的带束层，这里的结构突变造成了胎肩应力集中，因此带束层胶的应力应变增大，内耗增大。总的来说，支撑块的添加虽然使带束层胶的滚动阻力增加，但是仍然起到了降低整个轮胎滚动阻力的作用。

5 结 论

本文根据滚动阻力理论计算公式，用ABAQUS软件做了255/30R22轮胎和三角平衡轮廓轮胎以60 km/h自由滚动的模拟对比，得出结论如下：

(1) 三角平衡轮廓轮胎的滚动阻力仅18.7N，低于255/30R22轮胎滚动阻力的二分之一。支撑块主要降低了胎面和胎侧的滚动阻力，但增加了带束层胶的能耗，总的来说三角平衡轮廓轮胎的滚动阻力是显著降低的。

(2) 三角支撑块会造成胎肩的应力集中，导致带束层胶的内耗增加，后期可以从优化支撑块结构和改变材料方面来缓解应力集中现象，进一步降低三角平衡轮廓轮胎的滚动阻力。

参 考 文 献：

[1] 程钢，赵国群，管延锦，等.滚动轮胎热分析研究进展[J].弹性体,2007,17(4):59-62.

[2] Ebbott T G，Hohman R L，Jeusette J P，et al.Tire temperature and rolling resistance prediction with finite element analysis[J].Tire Science and Technology，1999，27(1)：2-21.

[3] Shida Z，Koishi M，Kogure T.A rolling resistance simulation of tires using static finite element analysis[J].Tire Science and Technology，1999,27(2)：84-105.

[4] 薛梓晨，贺建芸，杨卫民，等.三角平衡轮廓轮胎力学性能的研究[J].北京化工大学学报,2013,40(5):93-99.

[5] 祝爱兰，李洪元，吴立明.热塑性聚酯弹性体[J].弹性体,2005,15(1):70-75.

[6] 李侃社,王琪.导热高分子材料研究进展[J].功能材料,2002,33(2):136-136.

[7] 张帅,马永梅,王佛松.导热绝缘高分子复合材料的研究[J].塑料,2007,36(3):41-45.

[8] 高称意.轮胎用骨架材料的性能及其与轮胎性能的关系[J].弹性体，2002,12(2)：71-73.

[9] 王国林,董大鹏,何志刚,等.全钢载重子午线轮胎稳态温度场试验及仿真分析[J].橡胶工业，2009,56(9)：557-561.

[10] 危银涛,刘宇艳,杜星文,等.子午线轮胎滚动阻力与温度场非线性有限元分析[J].橡胶工业，1998,18(6)：330-336.

[11] 叶进雄.全钢载重子午胎滚动阻力有限元仿真与试验分析[D].北京：清华大学，2007:20-22.

[12] 庄茁，张帆，岑松，等.ABAQUS非线性有限元分析与实例[M].北京：科学出版社，2004.

[13] 杨卫民.轮胎设计与制造工艺创新的发展方向[J].中国科学技术大学学报，2013，39(2)：21-26.