变电站噪声智能预测及其主动控制

姜鸿羽，马宏忠，姜宁，李凯

(1.河海大学能源与电气学院，江苏南京211100; 2.江苏省电力公司南京供电公司，江苏南京210008)

变电站噪声智能预测及其主动控制

姜鸿羽1，马宏忠1，姜宁2，李凯2

(1.河海大学能源与电气学院，江苏南京211100; 2.江苏省电力公司南京供电公司，江苏南京210008)

针对变电站噪声有源控制技术中存在的算法性能较差和易受周边环境影响的问题，本文利用人工神经网络、小波技术及遗传算法对该技术进行改进。首先结合小波技术和人工神经网络来预测噪声控制系统的参考输入信号，然后根据小波去噪原理滤除进入误差传感器的混合噪声中由周边环境引起的高频干扰噪声，并将剩余噪声反馈至系统控制器中，最后利用遗传算法优化控制器中小波神经网络的参数，实现变电站噪声的最佳控制。对变电站内变压器振动和噪声数据进行仿真，结果表明改进后的方法有效地提高了系统的噪声跟踪速度、降噪量及稳定性，可以使变电站降噪达到满意的效果。

变电站噪声;噪声预测;小波神经网络;遗传算法

1 引言

随着变电站与居民生活区距离的缩短，变电站的噪声污染已经对居民的正常生活产生了不可忽视的影响。变电站噪声主要源于大型变压器运行产生的低频噪声［1］，但传统的被动噪声控制技术只对中、高频噪声有效，对低频噪声的控制效果并不理想［2］。为了有效地控制低频噪声，国内外许多学者将自适应有源噪声控制技术应用于变压器噪声抑制问题。文献［3］针对某110kV变压器，运用多声源阵有源控制策略对其低频噪声进行有源控制，通过实验验证取得了一定的消噪效果。文献［4］利用正余弦信号合成与源噪声信号相位相反、幅值相同的次级声源信号，实现抑制变压器噪声。文献［5］将一个可以控制和放大噪声的扬声器放置在变压器旁，使其输出与变压器噪声相位相反的噪声，达到消除噪声的目的。

尽管这些研究能够取得一定的降噪效果，但是效果并不理想，其原因主要有以下两点:①利用自适应有源控制技术时，次级声源的反馈和变压器周边环境变化引起的噪声会对有源消噪系统的稳定性和有效性产生很大的影响;②自适应滤波算法性能较差。针对这两个问题，本文首先利用变压器表面的振动信号和某接收点处的噪声信号建立基于小波变换和人工神经网络的噪声预测模型，并将预测的噪声信号作为自适应控制系统的参考输入信号，然后利用小波滤波器对含有次级噪声信号、变压器噪声信号及环境干扰噪声信号的混合噪声信号进行去噪，最后将滤除环境干扰噪声后的残余噪声信号反馈至控制器，并利用遗传算法优化控制器中小波神经网络的参数，实现对变电站内变压器噪声的最佳控制。

2 变电站噪声的预测

为了避免次级声源和变压器周围环境噪声对采集参考输入信号的干扰，本文利用人工神经网络［6］预测变压器噪声信号，并将其作为参考输入信号。变压器噪声主要来源于铁芯磁致伸缩变形和绕组电磁力所引起的振动，振动的幅度会随变压器运行状态的变化而变化。当变压器发生故障时，油箱振动会加剧，噪声会变大;当变压器所接负荷发生变化时，振动和噪声也会随之而变化。因此，在利用变压器表面振动信号预测接受点处噪声信号时，应该考虑将变压器不同运行状态下的振动信号和接受点处噪声信号作为训练样本，这样才能更全面地反映出振动与噪声之间的非线性关系。

为使预测的信号更加逼近真实信号，只有增加训练样本和训练的次数，才能获得理想的效果。然而，庞大的数据会严重影响神经网络的收敛速度和预测误差精度，故本文引入小波技术［7，8］来解决该问题。变压器正面某接受点处噪声预测步骤如下:

(1)利用MATLAB对实测的振动和噪声数据样本分别进行小波分解，提取小波分解系数编程为:

式中，x为信号;m为分解的层数;db3为小波函数。

(2)从小波分解系数中提取第m层小波低频系数，其编程为:

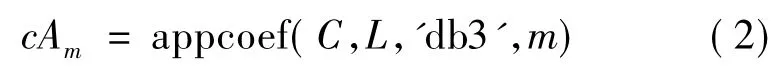
(3)将振动信号的小波系数和噪声信号的小波系数按式(3)归一化后作为神经网络的输入-输出对，建立预测模型。

式中，xmin、xmax分别为样本中最大值和最小值。经归一化处理后的样本在［0，1］之间变化。

(4)在测试阶段，将多通道振动信号的小波低频系数归一化后输入神经网络，预测出相应的噪声信号小波低频系数，再利用小波重构将其还原成噪声信号，小波重构的编程为:

步骤流程图如1所示。

图1 变压器噪声预测流程图Fig.1Transformer noise prediction flow chart

利用上述方法预测噪声还有如下优点:①第m层小波低频系数的数据量仅是原样本信号数据量的1/2m，所以该方法可以减少神经网络的运算量，提高网络的收敛速度和预测误差精度;②小波低频系数包含信号的主要信息，能够表征信号的特征，而高频系数往往与环境干扰噪声联系在一起，因此该方法可以避免因变压器实测噪声数据中含有环境干扰噪声而导致预测模型不准确的问题。

3 变电站噪声的控制

根据引言的分析可知变压器噪声控制效果不理想的原因有算法问题，也有许多实际因素的影响问题。

目前最为广泛使用的滤波算法是F-XLMS算法，但是由于声学通道的非线性，使其控制噪声的效果很不理想，因此许多学者将具有非线性处理能力的BP神经网络算法［9］应用到该控制系统中。由于BP神经网络算法存在收敛速度慢和容易陷入局部极小值等缺陷，其噪声控制的效果也不理想。另外，变压器周边环境变化所引起的非线性、突变、高频噪声，如工地施工的声音，人说话的声音，过往车辆的鸣笛声音等，将会随着残余噪声信号一起输入误差传感器中，使整个自适应控制系统不稳定，消噪效果降低。鉴于此，本文利用遗传小波神经网络算法代替传统的BP算法，并在误差传感器后加上小波滤波器，运用小波去噪原理祛除变压器周边环境变化引起的高频干扰噪声。

3.1 基于小波神经网络的自适应有源噪声控制

以小波基函数为神经元激励函数的小波神经网络应用广泛，与传统BP神经网络相比有以下优点:①网络在学习的超几何平面上每次调整的误差幅度较大，提高了收敛速度;②小波神经网络较强的灵活性使得网络逼近能力更具伸缩性。

小波去噪［7，8］先将原信号通过低通滤波和高通滤波后得到近似系数和细节系数，然后用门限阈值对分解得到的小波系数进行分析和处理以达到将有用信号和噪声分离的目的，最后对处理过的小波系数做逆变换重构信号，即可得到去除高频干扰信号后的低频有用信号。基于小波神经网络和小波滤波器的自适应有源消噪结构如图2所示。

图2 自适应有源消噪结构图Fig.2Adaptive active noise cancellation structure

图2 中，p(n)为实际的变压器噪声信号，x(n)为由神经网络预测得到的变压器噪声信号，d(n)为期望输入信号，v(n)为变压器周围环境变化所引起的干扰噪声信号，y(n)为控制器输出信号，s(n)为经过次级噪声通道的次级信号，e(n)为滤除干扰噪声后的残余噪声信号。设Hp(z)为初级噪声通道的传递函数，Hs(z)为次级噪声通道的传递函数，则d (n)=p(n)*hp(n)，s(n)=y(n)*hs(n)(*表示卷积)，e(n)=d(n)－s(n)。

本文的小波神经网络为三层，输入层、隐含层及输出层神经元数目分别为I、H和1;第n时刻输出层神经元输出为y(n);第n时刻隐含层神经元j的输出为Yj(n);第n时刻输入层神经元k的输入为xk(n)=x(n－k+1);第n时刻输入层神经元k到隐含层神经元j的连接权为ωkj(n);第n时刻隐含层神经元j到输出层神经元的连接权为Wj(n);第n时刻隐含层神经元j小波基函数平移因子和伸缩因子分别为bj(n)和aj(n);第n时刻隐含层神经元j的阈值为THj(n);第n时刻输出层神经元的阈值为th(n);则第n时刻隐含层神经元j的输出为:

第n时刻输出层神经元输出为:

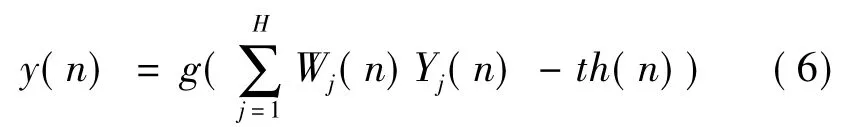
式中

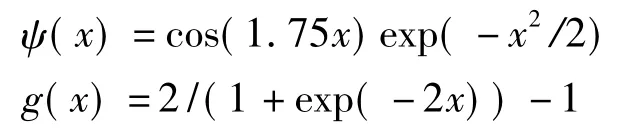
第n时刻自适应有源消噪系统的误差为:

为使系统误差逐渐减小至稳定值，利用梯度下降原理修正网络系数和小波函数的伸缩因子、平移因子。当新的数据输入自适应控制器时，便以新的网络参数计算系统误差。随着信号的输入，不断重复上述过程。

尽管小波神经网络提高了BP算法的收敛速度，但是其依然存在BP算法易陷入局部极小值的固有缺点，故本文运用具有全局优化能力和良好适应能力的遗传算法优化小波神经网络的参数，最终将逼近全局最优值的各个参数应用于小波神经网络，实现变压器噪声的最优控制。

3.2 遗传算法优化小波神经网络参数

遗传算法的并行随机全局性可以有效地克服小波神经网络容易陷入局部极小值的问题。为了方便，本文在固定网络结构下，利用遗传算法优化小波神经网络的参数［10］，具体步骤如下:

(1)根据网络结构确定染色体长度，并随机产生若干个初始染色体。

(2)由于实数编码可以缩小搜索空间和计算时间、提高搜索效率，所以对每一个染色体进行实数编码，每个染色体对应一组网络参数。本文将小波神经网络第n时刻的各个权系数ωkj(n)、Wj(n)和阈值THj(n)、th(n)以及隐含层神经元的平移伸缩因子bj(n)、aj(n)按一定的次序排列，形成一个实数染色体，其编码形式为:

?

(3)由于实测数据值较小，若以F(n)=1/(1+ E(n))为适应度函数，各染色体间差距会很小，不利于选择。为了拉开染色体之间的差距，本文按式(8)计算第n时刻群体中每个染色体的适应度。

(4)利用轮盘赌法来选择染色体，然后对当前一代群体进行交叉和变异的操作，最后生成新的一代群体。

(5)循环步骤(3)和(4)，每循环一次，就会得到一代新的群体，当达到最大遗传代数时，便停止循环，并将最新代群体中适应度最高的染色体解码得到相应的网络参数。

3.3 基于遗传小波神经网络的自适应有源噪声控制

虽然遗传算法具有全局优化的优点，但是较多的种群数量和迭代次数使得遗传算法计算量很庞大，这将导致自适应控制器无法精确地跟踪期望输入信号，严重影响噪声控制的效果。鉴于此，本文只在开始时利用遗传算法优化网络参数，使误差|e(n)|迅速下降，当其达到设定的值时，再用梯度下降原则对参数进行精调。噪声控制的具体步骤如下:

(1)利用神经网络预测出自适应消噪系统的参考输入信号x(n)。

(2)利用基于小波神经网络的控制器对参考信号进行处理，产生输出信号s(n)。

(3)利用小波滤波器处理进入误差传感器的混合噪声信号，并将处理后的残余噪声信号反馈至控制器。

(4)判断误差|e(n)|是否大于设定的误差值，若是则转第(5)步，否则转第(6)步。

(5)利用遗传算法优化网络参数，并将优化后的参数应用于小波神经网络，然后转第(7)步。

(6)利用梯度下降原则修正网络参数，并将优化后的参数应用于小波神经网络，然后转第(7)步。

(7)当新的数据输入至控制器时，重复步骤(2)、(3)和(4)，直至处理完所有数据。

4 计算机仿真分析

使用遗传小波神经网络算法实现变压器噪声的主动控制，首先需确定预测模型的样本数据，并进行相应的预处理，其次确定小波神经网络的结构和遗传算法的参数，最后对数据进行降噪处理。

4.1 噪声预测效果分析

根据第2节的分析知变压器的振动、噪声信号与它的运行状态密切相关，因此为了更准确地预测出变压器在不同运行状态下的噪声，用于训练的样本应该具有多样化，即在变压器不同运行状态下采集振动和接受点处噪声数据样本。

在绝大数情况下变压器都处于非故障状态，且其运行状态的变化呈现一定的规律性，如在一个季度的每一天中变压器负荷的变化趋势基本相同。为了简便，本文仅用变压器在一天中上午、下午、晚上及夜间四个时间段的振动和噪声数据来模拟变压器在四种不同运行状态下的振动和噪声数据样本。采集数据的方法如下:在南京市江东门110kV变电站内，将五路振动传感器分别吸附在户外某大型变压器油箱正面中部、顶面中部、底面中部及两侧散热器中部，用以采集变压器振动数据。麦克风放置在变压器正面0.5m处，采集相应噪声数据。数据均以电压信号的形式储存在PC机中。

考虑到预测模型的收敛性能，本文只从四个不同时间段内采集的振动和噪声数据中各选取500组，其中前325组作为离线训练数据，后175组作为在线测试数据。根据第2节预测噪声的步骤，本文首先利用db3小波函数对训练数据进行1层小波分解，得到第一层小波低频系数，然后将归一化后的小波系数用来训练四层BP神经网络，其中输入层有五个神经元、输出层有一个神经元，两个隐含层的神经元个数根据训练情况选择最优的。通过大量的试验发现当第一个隐含层包含20个神经元、第二个隐含层包含60个神经元时，BP网络训练效果最佳。隐含层激励函数均为双曲正切S型传递函数tansig，输出层激励函数为线性函数purelin，网络的学习精度为0.01，学习速率为0.04，动量系数为0.9。BP神经网络训练误差学习曲线如图3所示。

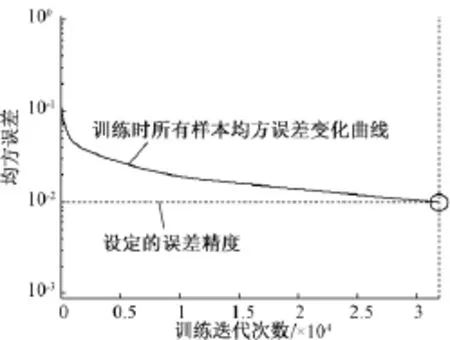
图3 BP神经网络训练误差学习曲线Fig.3BPNN training error learning curve

BP神经网络迭代31851次后，网络达到预设的收敛误差精度。当神经网络完成训练后，将用于测试的振动数据第一层小波低频系数输入该预测模型中，预测出接受点处噪声数据的第一层小波低频系数，再利用小波重构噪声数据。预测的噪声与实际的测试噪声分析如图4～图6所示。

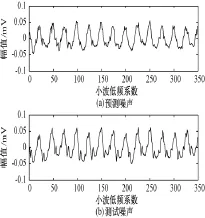
图4 噪声的小波系数Fig.4Noise wavelet coefficients

通过图4看出预测噪声的小波低频系数和测试噪声的小波低频系数在整体变化趋势、幅值上几乎相同，说明该预测模型具有较高的可靠性。通过图5和图6看出由小波重构的预测噪声波形比测试的噪声波形更加光滑而且预测噪声只含有低频有用部分，说明重构的噪声可以有效地祛除环境中高频干扰噪声，保留真实的信号。由此可见，用该法获取变压器低频噪声是可行、有效的。

4.2 噪声控制效果分析

为了体现遗传小波神经网络算法的优越性能，本节分别利用遗传小波神经网络算法和传统BP神经网络算法进行噪声抑制，并将二者的效果进行比较。

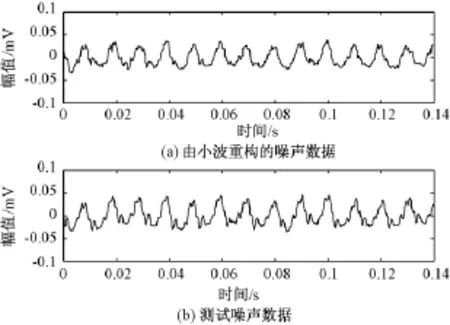
图5 噪声数据时域分析Fig.5Noise data time domain analysis

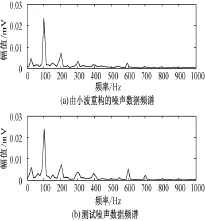
图6 噪声数据频谱分析Fig.6Noise data spectrum analysis

在遗传小波神经网络中，小波神经网络的结构为4-12-1，隐含层神经元激励函数为Morlet小波函数，输出层激励函数为Sigmoid函数，学习速率为0.09，动量因子为0.735。遗传算法种群的规模为50，最大遗传代数为20。根据染色体编码方式，每个隐含层节点有5个权系数、1个尺度因子、1个平移因子和1个阈值，再加上输出层的1个阈值，故染色体总长度为97。交配率为0.9，变异率为0.09。在BP神经网络中，网络结构同为4-12-1，隐含层激励函数为Sigmoid函数，输出层激励函数为purelin函数。在小波去噪环节中，以sym5为小波基函数，将输入信号进行2层分解，然后对分解得到的小波系数采用默认阈值消噪处理。

次级噪声、变压器噪声及变压器周边环境变化引起的噪声一起输入误差传感器，经过小波去噪和系统控制器处理后，误差信号e(n)的曲线如图7所示，误差曲线的频谱如图8所示。

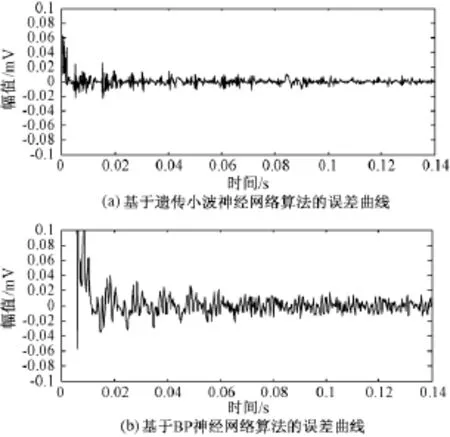
图7 两种算法的误差曲线Fig.7Error curves of two algorithms

图8 两种算法误差曲线的频谱Fig.8Spectrum of error curves of two algorithms

通过图7(a)和图7(b)，可以看出遗传小波神经网络滤波算法在0.03s(迭代150次)后开始收敛，BP神经网络滤波算法在0.07s(迭代350次)后才开始收敛，而且前者的收敛精度明显高于后者。通过图8(a)和图8(b)，可以看出遗传小波神经网络滤波算法可以有效地抑制变压器噪声，只剩余较少的本底噪声，而BP神经网络滤波算法的控制效果则较差。

自适应滤波算法的优劣除与收敛速度、收敛精度有关，还与算法稳定性有关。为比较算法的稳定性，本文在相同的条件下利用这两种滤波算法对相同的数据进行多次处理，分析期望输入信号d(n)和次级噪声信号s(n)的均方根误差变化范围，结果见表1。

表1 两种算法处理后的均方误差变化表Tab.1Two algorithms mean square error table

从表1可以看出，BP神经网络滤波算法的RMSE偏差范围大于遗传小波神经网络滤波算法的RMSE偏差范围，说明后者更稳定。同时还可以明显地看出，遗传小波神经网络滤波算法的RMSE平均值小于BP神经网络滤波算法的RMSE平均值，进一步验证了遗传小波神经网络滤波算法在收敛精度上的优越性。

5 结论

本文将噪声预测方法和自适应有源消噪方法组合应用于变电站内变压器噪声抑制问题。得到以下结论:

(1)融合了BP神经网络和小波变换技术的噪声预测模型具有较高的准确性和可靠性。

(2)小波滤波器可以有效地滤除变压器周围环境变化引起的非周期、突变、高频噪声，增强了噪声控制系统的稳定性和有效性。

(3)通过对变电站内某变压器实测数据的应用，得出遗传小波神经网络算法能有效地提高噪声控制系统的收敛速度、收敛精度及稳定性能。

本研究为今后变电站降噪装置的研制开发提供了一种新的思路。

［1］祝志祥，韩钰，聂京凯，等(Zhu Zhixiang，Han Yu，Nie Jingkai，et al.).变电站降噪用铝纤维吸声材料(Research on sound-absorption material of aluminum fiber for substation noise reduction)［J］.中国电力(Electric Power)，2012，45(7):57-61.

［2］李冰，胡国清(Li Bing，Hu Guoqing).降低变压器噪声的措施初探(Discussion on measure of reduction of transformer noise)［J］.变压器(Transformer)，2004，41(8):40-42.

［3］马玺越，陈克安，胡涵(Ma Xiyue，Chen Kean，Hu Han).110kV变压器有源噪声控制系统电声器件布放优化设计(Layout optimization of electro-acoustic devices of active noise control system for 110 kV transformer)［J］.噪声与振动控制(Noise and Vibration Control)，2011，(6):109-115.

［4］Qiu Xiaojun，Li Xun，Ai Yanting，et al.A waveform synthesis algorithm for active control of transformer noise: implementation［J］.Applied Acoustics，2002，(63): 467-479.

［5］C F Ross.Experiments on the active control of transformer noise［J］.Journal of Sound and Vibration，1978，61 (4):473-480.

［6］曾向阳(Zeng Xiangyang).基于神经网络法的舱室噪声预测(Neural network based cabin noise prediction)［J］.西北工业大学学报(Journal of Northwestern Polytechnical University)，2004，22(4):492-494.

［7］James S Walker.A primer on wavelets and their scientific applications［M］.Wisconsin:Chapman＆Hall，1999.

［8］关履泰(Guan Lvtai).小波方法与应用(Application of wavelet method)［M］.北京:高等教育出版社(Beijing:Higher Education Press)，2007.

［9］史忠植(Shi Zhongzhi).神经网络(Neural network)［M］.北京:高等教育出版社(Beijing:Higher Education Press)，2009.

［10］刘美容，何怡刚(Liu Meirong，He Yigang).遗传小波神经网络的非线性模拟电路故障诊断方法(Research on fault diagnosis method for nonlinear analog circuits based on GA，BPNN and wavelet)［J］.微电子学(Microelectronics)，2009，39(6):864-868.

Substation noise intelligent prediction and active control

JIANG Hong-yu1，MA Hong-zhong1，JIANG Ning2，LI Kai2
(1.College of Energy and Electrical Engineering，Hohai University，Nanjing 211100，China; 2.Nanjing Power Supply Company，Nanjing 210008，China)

In view of the deficiencies of substation noise active control technology，such as the poor performance of filtering algorithms and susceptible to the surrounding environment，this article uses artificial neural network，wavelet technology and genetic algorithm to improve the noise active control technology.First，using wavelet technology and artificial neural network algorithm the noise control system’s reference input signal is predicted.Then，according to the principle of wavelet de-noising high-frequency interference noise caused by the surrounding environment is removed which is included in the mixed noise into the error sensor，and the residual noise is fed back to the system controller.Finally，using genetic algorithm the parameters of wavelet neural network in the system controller are optimized，and optimal control of substation noise is achieved.Through the simulation of substation transformer vibration and noise data，the results show that the improved method can effectively improve the system noise tracking speed，noise reduction and system stability，and has better suppression effect for substation noise.

substation noise;noise prediction;wavelet neural network;genetic algorithm

TM401

A

1003-3076(2014)09-0074-07

2013-10-14

国家电网公司总部2011年重点科技项目(2011-0810-2251)

姜鸿羽(1989-)，男，江苏籍，硕士研究生，研究方向为电力设备状态检测与故障诊断;马宏忠(1962-)，男，江苏籍，教授，博导，研究方向为电力设备状态监测与故障诊断、电能质量监控。