增强型LMS自适应电网畸变电流检测算法研究

李文江，安丽，刘爽

(辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105)

增强型LMS自适应电网畸变电流检测算法研究

李文江，安丽，刘爽

(辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105)

为解决常规LMS自适应算法在电网畸变电流检测中存在收敛速度和稳态误差之间的矛盾，本文提出了一种增强型LMS自适应算法。该算法通过对输入信号环节进行预置带通滤波处理，改善信号的自相关数值，实现了基波处的幅值无衰减且相位无延时，同时通过对LMS算法权值和误差环节嵌入低通滤波拓扑结构，达到了降低畸变电流波动的目的。最后在对常规算法与增强型LMS算法分析比较的基础上，通过仿真和实验证明了本文理论分析的可行性，验证了此算法在畸变电流检测中的有效性和准确性。

电网畸变电流检测;LMS自适应算法;低通滤波器;增强型LMS自适应算法

1 引言

电网畸变电流的检测是控制电网供电质量的关键技术之一，如何快速准确地检测出畸变电流已成为检测技术中一个重要的研究方向。传统的检测方法有应用直接数据分析方法、傅里叶变换构成的FFT算法等常规检测算法［1］，然而这些方法都存在着很大的局限性。应用直接数据分析等常规方法适合于慢信号的谐波检测，当电网电流变化较快时，就不能够很好地跟踪动态变化，产生较大的误差。傅里叶变换构成的FFT算法在数字滤波器中确定电网谐波时，需要运用大量的输入电流采样数据，实时性差，不能很好地适用有源滤波实时补偿的要求。针对电网畸变电流谐波检测这一问题，本文对基于LMS自适应算法的电流检测方法进行深入分析，提出一种增强型LMS自适应电网畸变电流检测算法，运用低通滤波器滤去权值和误差迭代中的高频分量，提高了算法的稳态精度，加快了收敛速度。

2 LMS自适应电网畸变电流检测算法

2.1 LMS自适应算法检测原理

自适应检测算法是基于自适应噪声对消原理［2］，将设定的参考输入量调整为与负载电流基波分量大小和相位相同的分量，通过与负载电流抵消得到含有谐波电流与无功电流的输出。当外界参数发生改变时，通过自适应调整环节，自动调整检测算法。自适应算法以其良好的自适应性和鲁棒性在电网畸变电流检测中广泛应用，对频率和相位进行精确的跟踪。根据自适应噪声对消原理，电网畸变电流的检测算法如图1所示。

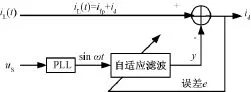
图1 电网畸变电流检测原理Fig.1Principle of grid distortion current detection

其中，id是畸变电流，ifp是非线性负载电流iL中的基波有功电流。根据噪声对消理论，ifp可以看成是噪声成分，畸变电流id可以看成信号成分，us是参考输入，经过滤波器后，输出最终逼近基波有功电流ifp，如果与iL相减，则得到id，从而实现了对非线性负载电流中畸变电流的检测。

LMS算法是一种基于最小均方误差准则，通过调节权系数使得滤波器的输出信号与期望响应信号之间的均方误差E［e2(n)］最小的算法［3，4］。基于LMS的自适应算法检测原理，利用LMS算法来使权值收敛至最佳权值，考虑到目前应用数字滤波的处理器速度较快，可使用瞬时估值误差的功率梯度来近似均方误差的梯度，即:

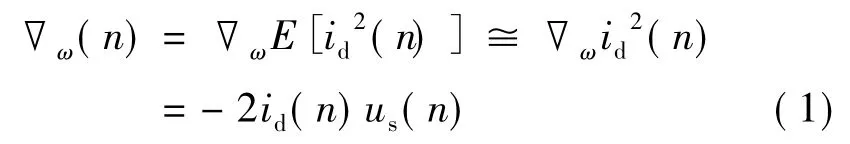
得到实用化的权值迭代更新公式，即:

设单相电网负载的电流、参考电压的采样信号分别为:

式中，N为每周期采样点数;M为负载电流的最高谐波次数;ak、bk为电流k次分量系数。令w(n)= K，则有:

为了避免Δw(n)差值过大，系数μ必须是一个取值比较小的参数，关系式(5)说明Δw(n)的数值和μ成正比。w(n)的波动意味着补偿电流id(n)是有误差的。

2.2 LMS自适应算法存在的缺陷

从式(6)中可以看出:增大μ值将会加快LMS的收敛速度，然而较大的最小均方误差E［i2d(n)］min也会产生较大的权值波动;权值波动加大会引起算法输出畸变，甚至导致系统不稳定。LMS算法的收敛速度与迭代步长成反比，而稳态失调误差与迭代步长成正比，LMS算法在收敛速率、瞬态跟踪及失调噪声(步长)之间的要求是相互矛盾的。即使采用变步长的LMS算法［5-7］在一定程度上解决收敛速度和稳态误差的内在矛盾，但算法本身不可能完全除去稳态误差。

3 增强型LMS自适应检测算法

当负载电流的幅值或频率发生变化时，现有的LMS自适应改进算法难以在获得较快收敛速度的同时兼具较小的稳态误差。为了实现对电网电流的动态检测，提高电网畸变电流检测的收敛速度与稳态误差，本文提出了一种增强型LMS自适应电网畸变电流检测算法。新型算法的基本思想是:在输入信号环节进行预置带通滤波处理，改善信号的自相关数值，实现基波处的幅值无衰减且相位无延时，达到快速跟踪的目的;同时在权值和误差环节嵌入低通滤波拓扑结构，用来降低畸变电流的波动［8］。此算法从根本上提高了稳态精度，加快了收敛速度。增强型LMS自适应算法检测原理如图2所示。

图2 增强型LMS自适应电网畸变电流检测原理Fig.2Principle of improved LMS adaptive grid distortion current detection

将傅立叶带通滤波器预置于自适应畸变电流检测系统的输入环节［9］，设滤波器采样频率为fs，基波频率为f0，输入序列为x(n)，则序列x(n)的傅立叶变换为:

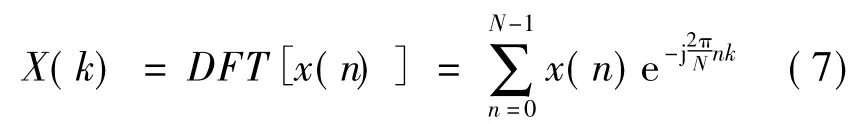
要使带通滤波器输出k次电流，分析该k次滤波器的频率特性，根据hk(n)的z变换:

由式(9)可知，该k次滤波器的相频和幅频特性分别是:

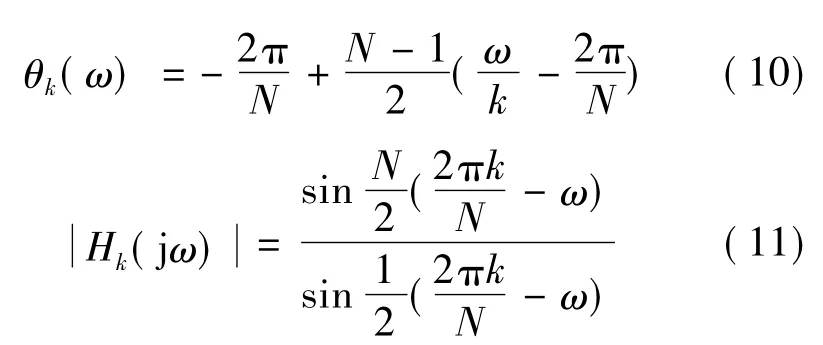
对于k次电流信号有ω=2πk/N，代入式(10)，有θk=－2π/N，当N足够大时，k次电流的相位移可以忽略不计，从而可以实现近似实时跟踪。幅频特性与相频特性如图3(a)、图3(b)所示。可见，该滤波器可以有效地滤除除指定的k次电流外的其他电流成分，提高畸变电流的跟踪速度，减小稳态误差。根据以上理论分析设计傅立叶带通滤波系统，如果系统的采样频率为fs=Nf0，则一个周期采样N个点。

为了进一步提高检测算法的性能指标，加快收敛速度，本文在输入环节进行预置带通滤波的同时，对LMS自适应算法的权值和误差环节嵌入低通均值滤波结构，可以平滑w(n)与id(n)的高频分量，改善收敛速度［10］。由图2可知增强型系统的权值输出为:

图3 基于k次电流信号处理的带通滤波器频率特性Fig.3Frequency characteristics of band-pass filter based on kthcurrent signal processing

根据式(5)，则有:

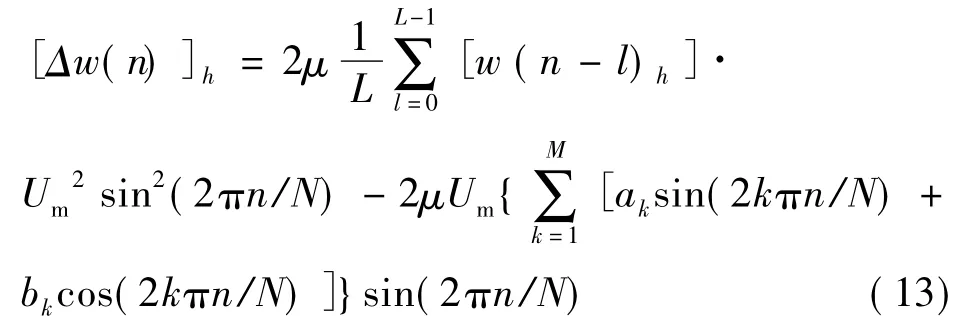
L为低通均值滤波器长度，简化表达式:

考虑μ→0，n→∞时，LMS自适应系统进入稳态。可知:

由上述分析可知，增强型LMS自适应检测算法可以降低畸变电流检测的波动，系统初始的收敛速度更快。

4 仿真分析

为验证本文所提出的增强型LMS自适应电网畸变电流检测算法的有效性和准确性，采用Matlab仿真软件进行仿真。设系统的输入为幅值在－10～+10之间变化、周期是0.02s、占空比50%的方波，参考输入是幅值为1并且与方波的基波同频同相的标准正弦信号。常规LMS算法的步长μ取0.04。增强型LMS算法在输入信号环节进行预置带通滤波处理，k≥2次的谐波分量被滤波器抑制，采样频率为6400Hz，则需要系统一个周期采样128个点;权值环节采用阶次为10的低通滤波器，通带截频为100Hz，误差环节采用阶次为20的低通滤波器，通带截频为300Hz。对本文提出的增强型检测系统进行仿真分析，并与传统的LMS自适应检测算法比较，观察基波有功跟随性能及其权值的变化如图4和图5所示，畸变电流的检测结果如图6所示，a、b分别表示基于常规LMS、增强型LMS自适应检测算法的波形。

图4 基波有功跟随性能对比波形图Fig.4Contrasted waveforms of active power following performance of fundamental wave

从仿真结果可以看出:增强型LMS自适应检测系统性能稳定，跟踪畸变电流效果明显优于常规LMS算法，收敛速度更快，只需1个周期就能达到稳定状态，进入稳态后权值波动趋于很小，大大降低了系统误差，有效地提高了稳态精度。

5 实验结果

基于本文提出的增强型LMS自适应检测算法，以TMS320C6410 DSP芯片为控制器设计了畸变电流检测系统，以单相畸变电流为例进行实验，将本文算法与增强型算法进行比较。实验结果如图7和图8所示。

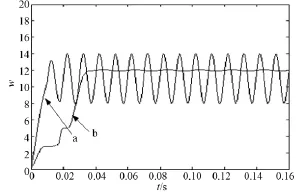
图5 基波有功权值变化波形Fig.5Waveforms of weighted changing fundamental active power

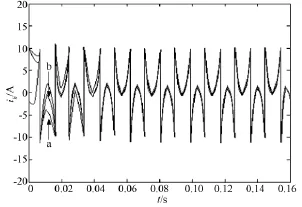
图6 畸变电流跟随性能Fig.6Following performance of distorted current

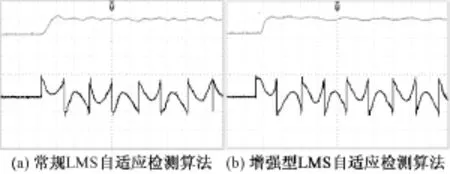
图7 初始权值与畸变电流波形Fig.7Initial weight and waveform of distorted current

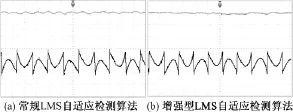
图8 稳态权值与畸变电流波形Fig.8Stable weight and waveform of distorted current

实验结果表明:在初始阶段增强型LMS自适应检测算法与常规的LMS算法相比具有更快的响应速度，能更快地到达稳定阶段，权值波动小，稳态精度高，电流畸变小。通过对比可以看出，该算法可以同时获得良好的收敛速度和稳态精度。

6 结论

本文提出了一种新的电网畸变电流检测方法，既能保证较快的收敛速度又能保持较高的检测精度，解决了传统方法存在收敛速度和稳态精度之间的矛盾，该增强型LMS自适应检测算法还可以应用到三相畸变电流检测系统中。

［1］盘宏斌，罗安，唐杰(Pan Hongbin，Luo An，Tang Jie).一种改进的基于最小二乘法的自适应谐波检测方法(An improved adaptive harmonic detection method based on least squares algorithm)［J］.中国电机工程学报(Proceedings of the CSEE)，2008，28(13): 144-151.

［2］罗安(Luo An).电网谐波治理和无功补偿技术及装备(The grid harmonic control and reactive power compensation technology and equipment)［M］.北京:中国电力出版社(Beijing:China Electric Power Press)，2006.

［3］K Mayyas，F Momani.An LMS adaptive algoritm with a new step-size control equation［J］.Journal of the Franklin Institute，2011，348(1):589-605.

［4］Junmin Zhang，Kaipei Liu.Harmonic detection for threephase circuit based on the improved analog LMS algorithm［A］.Proceedings of 11th International Conference on E-lectrical Machines and Systems［C］.Wuhan，China，2008.3978-3982.

［5］杨建宁，陈婕，关佳军，等(Yang Jianning，Chen Jie，Guan Jiajun，et al.).一种改进变步长的自适应谐波检测算法(An improved variable step-size adaptive harmonic detecting algorithm)［J］.电力系统保护与控制(Power System Protection and Control)，2011，39(6): 40-52.

［6］Paulo S R Diniz.自适应滤波算法与实现(Adaptive filtering algorithm and realization)［M］.北京:电子工业出版社(Beijing:Publishing House of Electronics Industry)，2004.

［7］何娜(He Na).电力系统谐波检测及有源抑制技术的研究(The detection and active mitigation methods for power system harmonics)［D］.哈尔滨:哈尔滨工业大学(Harbin:Harbin Institute of Technology)，2008.

［8］Liu Kaipei，Zhang Junmin.Harmonic detection based on the TLS estimation algorithm［A］.Proceedings of CES/ IEEE 5th International Power Electronics and Motion Control Conference［C］.Shanghai，China，2006.

［9］Shengkui Zhao，Zhihong Man，Suiyang Khoo，et al.Variable step-size LMS algorithm with a quotient form［J］.Signal Processing，2009，89:67-76.

［10］谷源涛(Gu Yuantao).LMS算法收敛性能研究及应用(Studies on the convergence performance of least mean square(LMS)algorithm and its applications)［D］.北京:清华大学(Beijing:Tsinghua University)，2003.

Improved LMS adaptive detection algorithm research in grid distortion current detection

LI Wen-jiang，AN Li，LIU Shuang
(Faculty of Electrical and Control Engineering，Liaoning Technical University，Huludao 125105，China)

In order to solve the contradiction between the convergence rate and steady-state error of conventional LMS algorithm，an improved LMS algorithm is proposed in this paper.The contributions of this paper are:(1)the proposed method applies the preset band-pass filter into the input signal link to improve the value of the autocorrelation of the input signal with no weakening of amplitude and no delay of phase in fundamental wave;(2)the low pass filter topology structure is imbedded into the algorithm weights of LMS and error link to reduce the fluctuation of aberrant current.The simulation results of the proposed method show that the proposed method has a faster convergence rate and less error.Based on the comparison between the proposed method and the conventional methods，the theory analysis in this paper is demonstrated to be feasible and the proposed method is proved to be more effective and accurate.

grid aberrant current detection;LMS adaptive algorithm;low-pass filter;improved LMS adaptive algorithm

TM714

A

1003-3076(2014)09-0057-05

2012-12-18

李文江(1951-)，男，蒙古族，辽宁籍，教授，博士生导师，研究方向为电力电子变流技术，工业自动化控制，电机与电器检测技术;安丽(1986-)，女，辽宁籍，硕士研究生，主要研究方向为节能型电力电子技术及应用。