基于人工蜂群算法与反向传播神经网络的铝热连轧轧制力预测

赵志伟， 杨景明， 车海军， 呼子宇， 王 茜

（1.燕山大学工业计算机控制工程河北省重点实验室，河北秦皇岛 066004；2.国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛 066004；

3.唐山学院计算机科学与技术系，河北唐山 063000）

基于人工蜂群算法与反向传播神经网络的铝热连轧轧制力预测

赵志伟1，2，3， 杨景明1，2， 车海军1，2， 呼子宇1， 王 茜1

（1.燕山大学工业计算机控制工程河北省重点实验室，河北秦皇岛 066004；2.国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛 066004；

3.唐山学院计算机科学与技术系，河北唐山 063000）

在分析传统的轧制力数学模型的不足之后，提出了一种基于人工蜂群算法与反向传播神经网络相结合的铝热连轧轧制力预测方法，使用人工蜂群算法优化反向传播神经网络的初始权值和阈值。以现场采集的精轧机组数据作为训练和测试样本，并与Sims数学模型和反向传播神经网络的预测结果进行比较，实验结果表明所提方法的轧制力预测精度和误差明显优于传统算法。

计量学；轧制力；神经网络；人工蜂群算法

1 引 言

在铝热连轧中，轧制力扮演着非常重要的角色，影响着轧制规程的设定，以及成品的板厚和板型。Orowan［1］，Sims［2］，Ford和Alexander［3］等人开发了各种数学模型，然而，由于现代轧制过程的复杂性，单纯的数学模型经常需要简化和假设，当这些假设不满足的时候，不可避免地就会引入误差，导致轧制力的预测出现较大的误差。为了解决数学模型的缺陷，Portmann等人将神经网络和经典的数学模型结合，提出了一个轧机控制系统的神经网络学习规程［4］。Lee等人提出了一个使用神经网络的长期学习方法来改善轧制力预测的精度［5］。Lee和Choi为轧制力设置提出了一个在线自适应神经网络［6］。本文在分析传统数学模型不足的基础上，为河南某铝厂的铝热连轧线精轧机组设计了一个基于人工蜂群算法与反向传播（BP：Back propagation）神经网络的轧制力预测方法，使用人工蜂群算法对神经网络进行优化，从而提高轧制力的预测精度，来改善产品质量。

2 传统的轧制力数学模型及统计分析

Sims公式是目前公认的最适合于热轧的理论公式，其轧制力模型采用以下形式［2］：

式中：P为轧制力，kN；B为带材宽度，m；l′c为考虑压扁后的接触弧长，mm；Qp为外摩擦应力状态系数；K为变形阻力；Kt为前后张应力对轧制力的影响系数。

为了检验传统数学模型的预测能力，本文采用河南某铝厂“1＋4”铝热连轧线精轧机组轧制1050A铝合金时第二机架的1472组数据作为样本进行统计分析，其他机架情况类似。图1显示了Sims数学模型预测的轧制力和实际轧制力之间的关系，只有25.48%的样本分布在与中心线偏差10%的范围内，并且Sims数学模型预测的轧制力明显偏大，因此该数学模型存在很大的误差。

图1 Sims模型预测的轧制力与实测值间的关系

3 人工蜂群算法优化BP神经网络

3.1 人工蜂群算法原理

人工蜂群算法（ABC）是2005年由Dervis Karaboga，受蜜蜂的智能行为激发而提出来的［7］。人工蜂群由3种蜂构成：雇佣蜂（Employed Bee）、观察蜂（Onlooker Bee）和侦查蜂（Scout Bee）［8］。假设有Ns个食物源，每个食物源对应一个解。雇佣蜂的数量Ne等于观察蜂的数量No，等于食物源个数Ns。每个解是一个D维向量，D代表需要寻优参数的个数。首先，ABC算法随机产生初始种群，种群大小为Ns，并设置解的最大更新次数和算法最大循环次数。然后，雇佣蜂开始在解的邻域内寻找新的解，如果新解的适应度值比旧解的大，则旧解被放弃，采用新解。计算这些解的概率值（Pi），观察蜂根据这些解的概率值（Pi）和采蜜蜂寻找的新解，再次在解的邻域内寻找新的解，并根据解的适应度更新解。如果某个新解的更新次数超过解最大更新次数，则该解就会被侦查蜂遗弃，用新解来代替。算法照此反复循环，直到达到最大循环次数，找到最优解。

3.2 基于人工蜂群算法的BP神经网络

在神经网络的应用中，80%～90%的模型采用了误差反向传播算法，即BP神经网络模型［9］。本文采用的BP神经网络由输入层、隐含层、输出层组成［10］。由于神经网络的初始权值和阈值对神经网络收敛精度和泛化能力有较大的影响，因此本文采用人工蜂群算法（ABC）对BP神经网络的初始权值和阈值进行优化。ABC优化BP神经网络步骤如下：

①创建一个BP神经网络并初始化ABC算法，包括蜂群数量Nc，雇佣蜂的数量Ne，观察蜂的数量No，解的个数Ns，解的最大更新次数，最大循环次数以及解的维数D，每个解包含了一组BP神经网络的权值和阈值。

②按照下式计算各解的适应度：

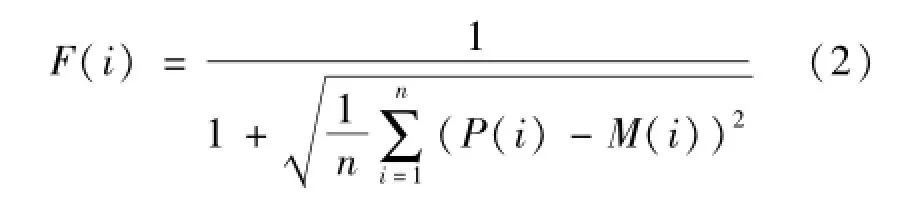
式中：n为样本数；P（i）为BP神经网络的轧制力预测值；M（i）为轧制力实测值。

③雇佣蜂按式（3）在解的邻域内搜索新解：

式中：i，k∈｛1，2，…Ns｝，j∈｛1，2，…D｝，k是随机产生的，并且k≠i；R为随机数，取值在［0，1］。然后按式（2）计算新解的适应度，如果新解的适应度大于旧解的适应度，则更新解，否则丢弃新解并在更新失败次数上加1。

④按式（4）计算各解的概率Pi，观察蜂根据解的概率在现有解的邻域内按式（3）搜索新解。

⑤如果解的更新失败次数超过解的最大更新次数，则放弃该解，按式（3）产生新解。

⑥如果迭代次数大于最大循环次数，则结束算法；否则返回③。

⑦算法结束，得到最优解，将最优解转换成权值和阈值，对神经网络进行训练和测试。

4 ABC-BP算法实验仿真

4.1 实验参数设定

通过对传统数学模型的分析，并结合现场实际生产经验，选择7个对轧制力影响比较大的参数作为BP神经网络的输入，分别是轧件宽度、轧件原始厚度、入口厚度、出口厚度、前张力、后张力和轧辊线速度。并选择双曲正切函数作为神经元传递函数，Levenverg-Marquardt反向传播算法作为神经网络的训练函数［11］。经过大量实验本文选择了隐含层有15个神经元的BP神经网络，蜂群数量Nc为200，最大更新次数为200，最大循环次数为200，维数D为121。

4.2 训练和测试样本的选择和处理

本文选取河南某铝厂“1＋4”铝热连轧线精轧机组轧制1050A铝合金时的7500组数据作为样本进行训练和测试，随机选择其中的5000组样本用于神经网络的训练，余下的2500组数据用来进行测试，所有样本数据均进行归一化处理。

4.3 实验结果及分析

直接使用样本对BP神经网络进行训练和测试后，BP神经网络的轧制力预测值和实测值之间的关系如图2所示。在2500个测试样本中，有98.28%的样本落在偏差10%的范围内，有83.04%的样本落在偏差5%的范围内。

对ABC算法优化后的BP神经网络进行训练和测试，ABC-BP算法的轧制力预测值和实测值之间的关系如图3所示。在2500个测试样本中，有99.84%的样本落在偏差10%的范围内，有95.04%的样本落在偏差5%的范围内。

为了能更好地对比3种方法的轧制力预测效果，表1列出了3种方法轧制力预测值与轧制力实测值之间的相关系数、均方根误差和绝对平均百分比误差。

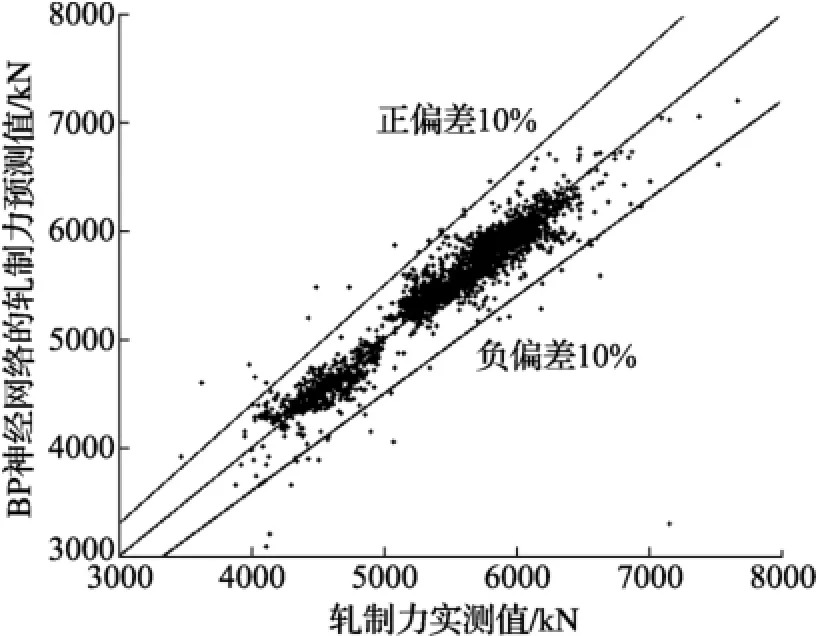
图2 BP神经网络的轧制力预测值与实测值间的关系

图3 ABC-BP算法的轧制力预测值与实测值间的关系

表1 算法的评价结果

通过对图1、图2、图3的对比，以及对表1的分析，ABC-BP算法轧制力的预测精度和误差明显优于前两者，并且有很强的鲁棒性。

5 结 论

本文在分析Sims数学模型的基础上，提出了将人工蜂群算法和BP神经网络相结合用于预测铝热连轧的轧制力。采用大量现场数据进行仿真实验，结果表明ABC-BP算法预测的轧制力精度和误差明显优于Sims模型和BP神经网络模型，为准确预测轧制力提供了又一种新的方法。同时，可以把扩大ABC-BP算法的应用范围作为以后研究的主题，比如板型预测、轧制力矩预测等。

［1］ Orowan E.The calculation of roll pressure in hotand cold flat rolling［J］.ProceedingsoftheInstitutionof MechanicalEngineers，1943，150（1）：140－167.

［2］ Sims R B.The calculation of roll force and torque in hot rolling mills［J］.ProceedingsoftheInstitutionof MechanicalEngineers，1954，168（1）：191－200.

［3］ Alexander J M，Ford H.Simplified hot－rolling calculations［J］.JINSTMET，1964，92：397－404.

［4］ Portmann N F，Lindhoff D，Sorgel G，etal.Application of neural networks in rolling mill automation［J］.Iron SteelEng，1995，72（2）：33－36.

［5］ Lee D，Lee Y.Application of neural－network for improving accuracy of roll－force model in hot－rolling mill［J］.ControlEngineeringPractice，2002，10（4）：473－478.

［6］ Lee D M，Choi SG.Application of on－line adaptable Neural Network for the rolling force set－up of a plate mill［J］.Engineeringapplicationsofartificial intelligence，2004，17（5）：557－565.

［7］ 苏彩红，向娜，陈广义，等.基于人工蜂群算法与BP神经网络的水质评价模型［J］.环境工程学报，2012，6（2）：699－704.

［8］ 罗钧，吴华，王强.具有快速收敛特性蜂群算法的球度误差评定［J］.计量学报，2011，32（6）：501－504.

［9］ 冯楠，王振臣，胖莹.基于自适应遗传算法和BP神经网络的电池容量预测［J］.计量学报，2012，33（6）：546－549.

［10］ 张媛媛，徐科军，许耀华，等.PSO算法结合BP神经网络在传感器静态非线性校正中的应用［J］.计量学报，2009，30（6）：526－529.

［11］ Hagan M T，Menhaj M B.Training feedforward networks with the Marquardt algorithm［J］.Neural Networks，IEEETransactionson，1994，5（6）：989－993.

Prediction of Rolling Force Based on Artificial Bee Colony Algorithm and Back Propagation Neural Network in Alum inum Hot Tandem Rolling

ZHAO Zhi-wei1，2，3， YANG Jing-ming1，2， CHE Hai-jun1，2， HU Zi-yu1， WANG Xi1
（1.Key Lab of Industrial Computer Control Engineering of Hebei Province，Yanshan University，Qinhuangdao，Hebei066004，
China； 2.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling，Qinhuangdao，Hebei 066004，China； 3.Department of Computer Science and Technology，Tangshan College，Tangshan，Hebei063000，China）

After analysing the traditionalmathematicmodel of rolling force，a predictionmethod of rolling force based on the artificial bee colony Algorithm and back propagation neural network is presented，which is used in aluminum hot tandem rolling.The initial weights and threshold values of back propagation neural network are optimized by artificial bee colony algorithm.The training and testing samples are collected from the finishingmills.Comparing with the Simsmathematical model and back propagation neural network，the experimental results show that the prediction accuracy and error of rolling force is superior to that of the traditionalmethods.

Metrology；Rolling force；Neural network；Artificial bee colony algorithm

TB931

A

1000-1158（2014）02-0157-04

10．3969／j．issn．1000-1158．2014．02．13

2013-06-13；

2013-09-25

国家科技支撑计划（2011BAF15B01）；国家冷轧板带及装备工程技术研究中心开放课题（2012005）；河北省工业计算机控制工程重点实验室开放课题（201112006）

赵志伟（1980－），男，河北唐山人，唐山学院讲师，燕山大学在读博士研究生，主要研究方向为冷热轧板厚板型智能控制。wzzwzz＠sina.com