水下摄影测量共线理论与相机标定方法

钦桂勤， 张永生， 黄桂平， 范亚兵， 陈 铮

（1.信息工程大学，河南郑州 450001； 2.华北水利水电大学，河南郑州 450011；3.61363部队，陕西西安 710054； 4.66444部队，北京 100042）

水下摄影测量共线理论与相机标定方法

钦桂勤1， 张永生1， 黄桂平2， 范亚兵3， 陈 铮4

（1.信息工程大学，河南郑州 450001； 2.华北水利水电大学，河南郑州 450011；3.61363部队，陕西西安 710054； 4.66444部队，北京 100042）

基于摄影光学理论，分析了相机在空气中和水下成像基点位置关系，提出水下摄影三点共线理论，并推导出相机在水下主距变化模型；分析了相机水下摄影视场和畸变大小的变化，设计了水下摄影测量相机标定方法；最后通过水下摄影试验标定，验证了水下摄影三点共线理论的正确性和水下相机标定方法的实用性。

计量学；水下摄影测量；三点共线理论；水下相机标定；相机主距；基点位置

1 引 言

水下摄影测量是双介质摄影测量的一种，属于一种非常规摄影测量［1，2］。传统观点认为，双介质摄影测量中，镜头的摄影中心位置同单介质摄影时相同，只是由物点发出的光线在界面处发生折射，从而导致物点、摄影中心和相应像点三点不再共线［1～9］。双介质摄影测量的这种折射理论，对于被测物和相机不在同一介质中（如在水面上对水下物体进行摄影）的情况是合理的，许多学者对此作了大量的研究［2～5］。对于摄影相机和被测物均在水下的测量，对此感兴趣的学者们也从折射的角度出发进行了大量的研究［6～9］。水下摄影测量成像系统与空气中成像系统不完全相同，目前有水下专用可与水直接接触的测量相机（镜头前有一块防水光学玻璃），也有将常规测量相机密封在相机防护装备中，因此相机水下防护装备也成为水下成像系统的一个组成部分［10］。关于水下相机标定方法，目前国内文献提到不多［11］；国外Fraser和Fryer的文章中提到采用解析铅垂线法和自检校方法［6］，Lavest提出可以通过水上标定的结果预测水下相机标定参数的初值［9］。

本文从摄影光学理论出发，详细分析了相机在空气中和水下成像特点以及成像系统基点位置关系，推导出“水下摄影三点共线”理论和主距变化关系；对相机水下摄影视场和畸变进行研究，总结出水下摄影测量相机标定模型和方法；最后通过试验对水下摄影测量相机进行标定，试验结果验证了本文提出的“水下摄影三点共线”理论的正确性和水下相机标定方法的实用性。

2 水下摄影测量共线理论

相机在水下成像过程同在空气中相似，但相机在水下成像时，由于物方空间介质与像方空间介质不一样，因此不能完全利用空气中相机成像模型和数据对水下摄影进行处理。

2.1 相机水下成像系统基点位置关系

成像光学系统的特性不仅与构成该系统的各个透镜组的结构有关，还与该光学系统的物方和像方所处介质的折射率有关［12，13］。当透镜结构一定时，成像光学系统基点位置和焦距（相关术语名称参看文献［13］）与物方空间和像方空间的折射率有关。相机在空气中摄影，也就是常规摄影，节点J（J′）与相应主点S（S′）重合，物镜的主点具有节点的特性——过主点的共轭光线彼此平行，物方焦距f和像方焦距f′大小相等［12，13］，如图1所示。当相机位于水下摄影时，节点与相应主点不重合，但是过节点的共轭光线仍然彼此平行，物方焦距和像方焦距大小不相等，如图2所示。

图1 空气中成像系统的基点位置关系

2.2 相机水下成像系统焦距变化

相机在水下进行摄影时，镜头前通常存在一平面壳窗玻璃，无论镜头在空气中还是在水中，镜头的像方焦距不变。因为从无穷远处平行透镜光轴的光线垂直于壳窗表面入射，如图3（a），而垂直入射光不偏折，所以光线通过壳窗不变。因此无论镜头在空气中还是在水中，像方焦点f′位置不变，像方主平面H′和像主点S′位置也不会发生改变，因此镜头的像方焦距f′大小也不变，同空气中一样大小。

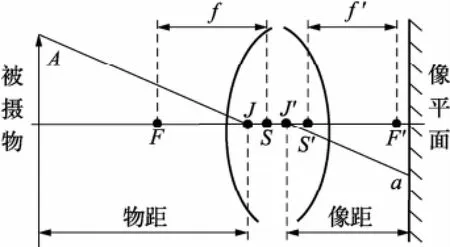
图2 水中成像系统的基点位置关系

但是相机在水中同在空气中其物方焦点和物方主平面将会发生变化。因为像方从无穷远处沿透镜光轴的光线平行进入透镜，并以倾斜的角度通过壳窗玻璃，如图3（b）。壳窗玻璃左边物方空间在水中和在空气中时，将会产生不同的效果。如果物方仍然为空气，物方焦点仍然在原处，图3（b）中虚线交点处（忽略壳窗平面玻璃的光学作用［10，11，14］）；如果物方为水，经过镜头出射的光线在壳窗处会再次发生折射进入水中，其光线将会明显相对空气中发生折射。物方焦点将向物体方向离开原空气中焦点的位置，而物方主点将会向像方空间离开原空气中主点的位置。

图3 镜头在水中焦点和主点位置变化

同一相机浸入水中和置于空气中，所构成的成像系统的参数满足下面的关系［12，13］：

式中：fa、f′a为相机在空气中的物方焦距和像方焦距；fw、f′w为同一相机在水中的物方焦距和像方焦距；nw为水相对空气的折射率。

相机镜头与壳窗玻璃构成的光学系统，其像方焦距、像方主点位置与物方空间折射率无关，即该成像系统在空气中的像方焦距、像方主点与在水中相等；但物方焦距、物方主点位置、物方节点和像方节点位置均与空气中不同。水下相机在空气中构成的光学系统对应主点和节点重合，在水下构成的光学系统对应主点和节点不重合。

2.3 水下摄影测量“三点共线”理论

摄影物镜成像时，物点发出许多光线，相应像点是这些光线相交的结果。如图4，物点A发出许多光线，经摄影物镜会聚后成像于a点。在这些光线中有一条光线通过节点，它由物点发出向物方节点方向投射，再经像方节点沿平行于入射方向射出，过节点的光线方向不会发生改变［13］。摄影测量中“三点共线”理论就是利用过节点的光线通过针孔成像模型建立物镜成像时的物像位置关系。如图5（a），A1、A2为物点，a1、a2为其对应的像点，P为像平面，J、J′为前节点和后节点，该图中物点和对应像点间的几何位置关系通过过节点的光线来表示。

图4 摄影物镜成像光线

图5 过节点的光线表示的物像关系

如果将图5（a）中像方节点连同像平面一起平移到物方节点，使像方节点与物方节点重合，当作一个点看待，那么物点、像点和节点都在一条直线上，类似于针孔成像，重合的节点为投影中心，也就是镜头中心。此时物点、像点和投影中心三点共线，这就是常规摄影测量中的经典“三点共线”理论［1，15，16］。

常规摄影时，物镜的节点正好与其对应主点重合，综合图1中节点和主点位置关系以及图5中节点关系，可以得到“重合的主点就是摄影中心”的推论。在实际摄影测量中，更多地称摄影物镜的主点为镜头中心［1，15］，因为常规摄影测量主要是指空气中摄影测量。

水下摄影测量的成像几何关系仍然可以利用针孔成像模型来描述，水下摄影测量的投影中心位置，为摄影物镜在水中构成的光学系统两节点的等效；像点仍然为物点和投影中心的连线与像平面的交点；物点和对应的像点以及投影中心三点共线；但水下摄影测量的投影中心与主点不重合［16］。

2.4 相机水下成像系统主距变化

大多数摄影测量，如航空摄影测量、近景摄影测量，成像位置可近似认为在透镜像方焦平面上，即相机镜头的像平面聚焦在焦平面［12，13］上。常规摄影测量中，当物体在镜头前10倍焦距以外，成像位置就可近似认为在透镜像方焦平面上。因此在近景摄影测量（包括水下摄影）中，一般可以将相机的像距近似看成投影中心（两节点的等效点）到像方焦点的距离，又称作相机主距。由文献［13］中牛顿公式可知，相机在空气中构成的光学系统主距f0a可近似为：

相机在水中构成的光学系统主距f0w为：

这里主距和焦距的符号只表示大小，不表示方向。综合式（1）～式（4）可得：

从而可得出同一摄影物镜水下摄影时相机主距近似等于空气中摄影主距与水的折射率的乘积，标准状况下水的折射率为1.333。水下摄影相机标定过程中，可以通过这种关系获取相机主距的初值，后面的试验将验证该推导的合理性。

3 水下摄影相机视场和畸变变化

相机浸入水中成像系统主距发生变化，也必然导致相机在水下视场发生变化。相机的像平面尺寸（CCD大小未变）没有发生变化，因此同一相机在水中的视场显然比在空气中小［9］，如图6所示。

假设水中和空气中成像没有任何畸变或者对畸变进行了改正，则同一物体的影像尺寸在水中应是空气中的1.333倍，即

式中：u为空气介质中某点的影像值，du为对应点的畸变改正值；同样uw为水中某点的影像值，duw为对应点的畸变改正值。

图6 空气中和水中相机视场变化

4 水下摄影测量相机标定

相机在水下成像也存在畸变，水下影像的畸变并不影响一般的水下观察任务，但对于水下测量或精确定位导航，则必须对水下影像畸变的系统误差进行校正。

4.1 相机标定数学模型

前面分析表明，水下摄影时，物方点（X，Y，Z）、镜头中心（XS，YS，ZS）（水下摄影时，摄影中心位置为节点J和J′的等效，与主点不重合，本文按常规方式以主点表示投影中心）和相应像点（x，y）三点共线，它们满足共线条件方程。事实上由于各种干扰因素的存在，使得像点在焦平面上相对其理论位置存在偏差（Δx，Δy），实际像点偏差的共线条件方程式为［11］：

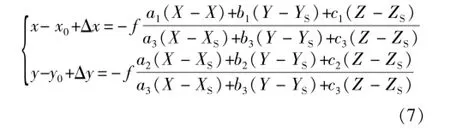
无论是常规摄影还是水下摄影，实际像点的偏差具有一定的规律性和重复性，是成像过程中诸多干扰因素影响的结果，如像机镜头的畸变、摄影材料的系统变形以及采用的内方位元素不准确等。而且这些像点坐标误差成系统性，故称之为像点的系统误差。原则上讲，像点的系统误差是像点坐标的函数，由于这种函数关系很难得知，所以存在许多不同的选择方案。可以从引起系统误差的物理因素出发，也可以用一般的数学模型去拟合［11］。

本文采用最常见的10参数模型建立像点系统误差，包含了径向畸变、偏心畸变、像平面畸变和内方位元素误差的影响，可写成如下矩阵形式［11］：

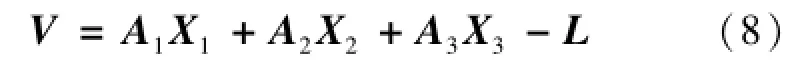
式中：V为像点坐标残差；X1、X2和X3分别为外方位元素、物方点坐标和内部参数，X1、X2、A1、A2和L的值参见文献［11］，X3和A3分别为：

X3即为待标定的参数，共有10个未知数，故将式（8）～式（10）称为数字像机标定的10参数模型，在实际应用中可以根据精度需要选择全部或部分参数进行标定。

4.2 水下摄影测量相机标定方法

水下摄影相机标定的方法和步骤与空气中相似，但在具体实现时，水下摄影相机标定存在以下特点：（1）试验场布置困难，需要布设在水下；（2）摄影设备必须能够在水下操作，设备状态应和具体摄影测量时一致；（3）水下摄影过程较空气中困难、复杂。

相机标定场和测量目标不在同一地点时，会带来很大的麻烦。考虑到以上因素，水下相机标定最好能够在线标定，而且在每次测量过程中都能进行自检校。本文采用光束法自标定对水下摄影相机进行标定，并且采用了水下相机主距与空气中相机主距的关系，根据空气中的相机标定结果对水下摄影相机主距赋初值。

光束法自标定对水下摄影相机标定的步骤：（1）在空气中对水下摄影设备进行光束法自标定；（2）水下摄影相机主距初值的计算；（3）获取水下控制架的影像数据；（4）利用物点对应不同影像上像点的关系建立像机标定的10参数模型，利用光束法平差进行解算。

非线性系统的最优解对初值很敏感，光束法自标定时必须考虑相机内参数的初值。无论在水上或水下，一般将畸变参数初值设为零，主点坐标初值也设为（0，0）；空气中相机主距初值设为其焦距值（镜头出厂标示值），水下相机主距初值设为空气中标定值的1.333倍。

5 水下摄影相机标定试验与结果

利用水下摄影测量共线理论与相机水下标定方法，对室内活动三维控制架进行3种不同的试验。（1）直接用尼康D700相机在空气中对控制架进行摄影测量；（2）将该相机安装到相机防护罩中在空气中对控制架进行摄影测量；（3）将该相机安装到相机防护罩中在水下对控制架进行摄影测量。每种试验获取3组数据，所有测量结果均用光束法自标定方法计算得到。

5.1 试验环境

三维控制架采用铝合金材料制成，其结构如图7（a），尺寸为0.8 m×0.5 m×0.5 m，中间有多个支架加固，可以认为是刚性的，即该天线放在水上和水下的形态一样，理论上不发生形变。

在控制架三个相互平行的平面上共布设了78个反光标志，标志点坐标采用专业测量相机INCA3获取影像数据，并通过美国GSI公司的工业摄影测量系统V-STARS测出这些标志点的三维坐标，其测量精度优于0.03 mm［17］。因此将INCA3相机测量的标志点作为后续外部检核精度的控制点。

试验采用尼康D700相机，如图7（c）；镜头为尼康AF尼克尔21 mm／2.8D，其视场角为81°×60°。相机防护罩为水下摄影测量专门研制的“水下精密摄影测量防水箱系统”［10］，防水箱玻璃窗口采用的是5 mm厚的K9玻璃，安装时让相机的镜头刚好贴紧石英硅玻璃，同时相机闪光灯也透过石英硅玻璃窗口，如图7（d）。

拍摄过程中相机设置是固定的，即相机焦距、光圈系数、曝光时间在水下和空气中设置不变，但闪光灯输出强度水下设置较水上大。

空气中相机标定在室内一平地面上，水中相机标定试验在塑料大桶中进行，桶高1.85 m，内径1.55 m，桶中水的深度为1.5 m，图7（b）所示。

5.2 试验过程

步骤（1）：直接用相机对空气中控制架进行摄影，分别在7个摄站位置对控制架共拍摄了23张像片，摄站位置示意如图7（f）。再用同样方法重复拍摄2组数据。

步骤（2）：将相机安装到相机防护罩中在空气中对控制架进行摄影，摄站位置和姿态基本同步骤（1），共拍摄3组数据。

图7 水下摄影试验相关图片

步骤（3）：将控制架放入桶底，向桶中注水，水位到达1.5 m即可，这样可以保证最小摄影距离为0.8m。利用上述步骤（2）中安装好的成像设备，对水下控制架进行摄影，采取同步骤（1）中类似的位置和姿态共拍摄23张像片。注意水中拍摄像片时，将紧贴镜头一面的防护装备没入水中2～6 cm，保证镜头在水下，如图7（e），拍摄3组数据。

5.3 试验数据处理

利用10参数模型根据光束法自标定算法计算出空气中相机参数；根据空气中相机标定的主距值，利用相机水下和空气中主距关系，获取水下相机主距初值，再通过10参数模型获取水下相机参数。

每个试验中有3组数据，任选一组试验数据列入表中。重复精度为每个试验中任选两组数据解算出的标志点坐标与第3组数据解算的结果差值的均方根。因此，每个试验中有2组重复精度，表中任列出一组作为代表。测量精度为通过本试验获取的控制架反光标志点坐标与在水上通过INCA3相机其测量值之间差值的均方根，每个试验有3组值，表中任列出1组作为代表。

5.4 试验结果与分析

3种试验自标定结果见表1。从表1可以看出，在空气中，相机安装防护罩，相机内参数会发生变化，但是相机主距值只发生微小变化，这是由相机本身的稳定性和防护罩的影响造成的。相机安装上防护罩后，其测量精度降低，这主要是由于加装防护罩后摄影系统的结构变复杂、稳定性降低所致。

表1 相机光束法自标定结果mm

水中相机主距的标定值（29.3 mm）为空气中加防护罩（22.0mm）的1.332倍，几乎等于水的折射率（1.333），充分验证了文中推导的主距变化关系。相机在水中测量精度（0.096 7mm）同空气中加装防护罩后测量精度（0.099 4 mm）接近，从而也验证了本文提出的水下摄影测量共线理论的正确性。

6 结 论

由于水对光的影响和水下摄影环境的不同，在水下获取的影像质量比空气中差一些，因此水下测量精度应该比空气中略低，但本试验结果却相反。分析原因，这是由于相机在水下主距增大导致测量精度提高的缘故。同样测量条件下，理论上相机焦距越大，其测量精度越高。从而可以这样推论，只要减小或消除相机防护罩对测量精度的影响并保证水下成像质量，同等条件下对同一物体测量，水下测量精度可以超过水上测量精度。本文推导的水下摄影测量共线理论，只适用于整个物方空间均在水下的摄影测量，不包括物方空间一部分在空气里另一部分在水下的情况。另外相机在水下，只需镜头的最前端没入水中即可，水下摄影测量“三点共线”理论成立。

［1］ 王之卓.摄影测量原理［M］.北京：测绘出版社，1979.340－345.

［2］ 邵锡惠.军事工程摄影测量［M］.北京：解放军出版社，1991.206－211.

［3］ 王有年，韩玲，王云.水下近景摄影测量试验研究［J］.测绘学报，1988，17（3）：217－224.

［4］ 单杰.双介质摄影测量的相对定向［J］.解放军测绘学院学报，1993，（3）：38－44.

［5］ 常本义.双介质摄影测量基本公式［J］.测绘学报，1991，20（4）：288－294.

［6］ Fryer JG，Fraser C S.On the calibration of underwater cameras［J］.Photogrammetricrecord，1986，12（67）：73－85.

［7］ Telem G，Filin S.Photogrammetric modeling of underwater environments［J］.ISPRSJournalof PhotogrammetryandRemoteSensing，2010，65（5），433－444.

［8］ LIR X，LI H H，ZOU Wei H，etal.Quantitative Photogrammetric Analysis of Digital Underwater Video Imagery［J］.IEEEJournalofOceanicEngineering，1997，22（2）：364－375.

［9］ Lavest JM，Rives G，Lapreste JT.Underwater Camera Calibration［J］.ComputerVision—ECCV2000，2000，1843：654－668.

［10］ 钦桂勤，范亚兵，蒋理兴.一种浅水摄影测量水下相机的防护装置［J］.测绘科学，36（4）：131－133.

［11］ 钦桂勤.模拟失重环境星载天线型面水下摄影测量技术研究［D］.郑州：解放军信息工程大学，2011.

［12］ 沙占祥.摄影镜头的性能与选择［M］.北京：中国摄影出版社，2004.65－69.

［13］ 郁道银，谈恒英.工程光学［M］.北京：机械工业出版社，2002.14－34.

［14］ 默顿斯L E.水中摄影学［M］.北京：科学出版社，1979.109－112.

［15］ 江延川.解析摄影测量学［M］.郑州：测绘学院，1991.1－27.

［16］ 钦桂勤，黄桂平，张永生.双介质摄影测量共线理论研究［J］.测绘学报，2011，40（3）：351－358..

［17］ 钦桂勤，黄桂平，卢成静.V-STARS数字摄影三坐标测量系统的精度测试及应用［J］.计量学报，2008，29（4A）：200－203.

Collinearity Theory and the Camera Calibration Method of Underwater Photogramm etry

QIN Gui-qin1， ZHANG Yong-sheng1， HUANG Gui-ping2， FAN Ya-bing3， CHEN Zheng4
（1.Information Engineering University，Zhengzhou，Henan 450001，China；
2.North China University ofWater Resources and Electric Power，Zhengzhou，Henan 450011，China；
3.Troops 61363，Xi'an，Shaanxi710054，China； 4.Troops 66444，Beijing 100042，China）

With a brief introduction of optical theory of photogrammetry，the relation of the location of datum marks is described in camera lens system between air and underwater.The collinearity theory of underwater photogrammetry is proposed，and the variety of principal distance of underwater camera is illustrated.After the analysis of distortion and view of underwater photography，the camera underwater calibration method is described.One calibration test on underwater camera was done.The results indicate that the collinearity theory of underwater photogrammetry is right and themethod of underwater camera calibration is suitable.

Metrology；Underwater photogrammetry；Collinearity theory of three points；Camera underwater calibration；Principal distance of camera；Location of datum marks

TB96

A

1000-1158（2014）02-0133-06

10．3969／j．issn．1000-1158．2014．02．08

2011-03-09；

2013-12-02

国家863计划（2008AA042410）

钦桂勤（1977－），女，湖北随州人，信息工程大学讲师，博士，主要从事视觉测量及传感器技术研究。qinguiqin＠sohu.com