二维精密工作台离散点测量结果误差分离的新方法研究
郭天太, 王晓晓, 洪 博, 赵 军, 孔 明, 高思田
(1.中国计量学院,浙江杭州 310018; 2.中国计量科学研究院,北京 100013)
二维精密工作台离散点测量结果误差分离的新方法研究
郭天太1, 王晓晓1, 洪 博1, 赵 军1, 孔 明1, 高思田2
(1.中国计量学院,浙江杭州 310018; 2.中国计量科学研究院,北京 100013)
针对测量结果中包含的误差,提出一种能够分离精密工作台系统误差的方法。首先利用辅助测量栅格板和二维精密工作台的不同位置进行测量,然后根据栅格板上标记点的测量数据和标称值建立误差分离的数学模型,最终实现对测量结果的误差分离。通过仿真验证了算法的有效性。仿真结果表明:当不存在测量噪声时,能够实现误差的完全分离;当存在测量噪声时,计算值与给定值标准差的相对误差在X轴和Y轴上分别为1.95%和1.52%。对于不同幅度的噪声,工作台系统误差计算值稳定。该算法对噪声不敏感,表现出很好的鲁棒性,可用于测量结果和仪器性能的评价。
计量学;误差分离;二维精密工作台;系统误差;测量结果;标准不确定度
1 引 言
误差分离技术最初由青木保雄等人提出[1],并应用于圆度误差的精密测量,通过对传感器输出的信号进行分析和运算,分离出回转轴运动误差和被测截面圆度误差。此后,该技术扩展至多步法和多点法圆度误差分离技术[2,3]。国内外研究主要集中于圆度及圆柱度等的误差分离。近年来对精密工作台定位精度的校准受到重视[4],J.Ye根据测量数据建立数学模型,并采用傅里叶变换算法计算工作台系统误差[5~7],该方法计算过程较为复杂,实际应用较少。朱煜、朱立伟等提出利用非线性优化法对二维超精密工作台运动建立测量模型[8~12],并未给出合理的迭代初始值求解方法。在此基础上崔继文等利用二维迭代模型来实现对二维工作台系统误差的分离[13]。但以上方法均存在模型求解复杂、不便于实用的问题。
本文提出一种针对精密仪器二维精密工作台离散点测量结果的误差分离方法,通过利用不同位置的测量数据来实现对测量结果的误差分离,为后续的误差修正提供依据。由于算法是对离散的点进行运算,给出的误差分离结果也是离散点的误差,因此,可把离散点及其附近区域看作是系统误差近似相等,即每一点的系统误差成分是低频的,利用离散点测量结果的不确定度来评价该方法的有效性。
2 误差分离方法
2.1 变量定义
二维精密工作台离散点误差分离方法的基本原理如下:借助于辅助测量栅格板(其精度可低于测量仪器的精度),当栅格板置于工作台不同位置时,测量数据中包含不同误差项。通过测量仪器读取辅助测量栅格板上标记点的测量数据,将测量数据、标记点标称值和相应的误差建立数学模型,利用最小二乘法对模型进行运算,最终分离出二维工作台测量点的系统误差和栅格板标记点的系统误差。

图1 误差分离算法变量示意图
首先建立坐标系(见图1)并定义变量。图1(a)表示工作台坐标系中测量点与实际位置的偏离(系统误差)以及坐标之间的关系,Gx(i)、Gy(i)分别为工作台第i个测量点系统误差值在X轴和Y轴方向的偏移量。图1(b)表示辅助测量栅格板标记点与实际位置的偏离(系统误差)及坐标之间的关系,Ax(i)、Ay(i)分别为第i个标记点系统误差值在X轴和Y轴方向的偏移量,Nx(i)、Ny(i)分别为栅格板第i个标记点的标称值。
为了建立数学模型,需要将图1所示的不同坐标系中的各变量统一于同一个定义坐标系中,如图2所示。图中包含3个坐标系:定义坐标系XOY、工作台坐标系XGOGYG、栅格板坐标系XAOAYA。后两个坐标系相对于定义坐标系的旋转角度分别记为θg和θa,其坐标原点相对于定义坐标系原点的偏移量分别记为(Vg,Wg)和(Va,Wa)。对于辅助栅格板上的标记点A,向量OP为其理想坐标值,向量PA为其系统误差;对于工作台上同一位置处的测量点A,向量AM为其系统误差。
图1和图2中理想坐标系的选取不是任意的,需满足下列条件[5,6]:
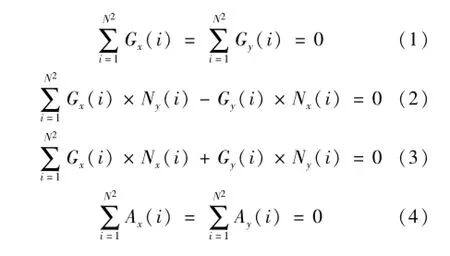
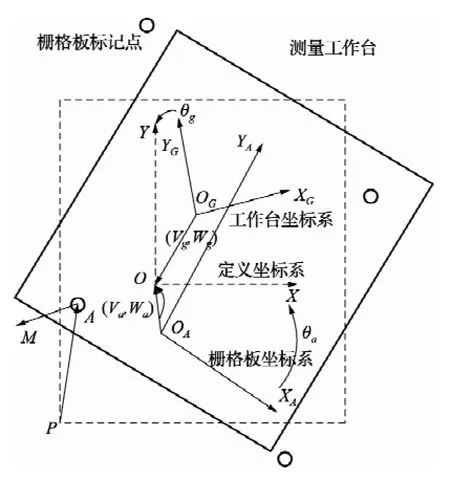
图2 定义坐标系及坐标系之间的转换
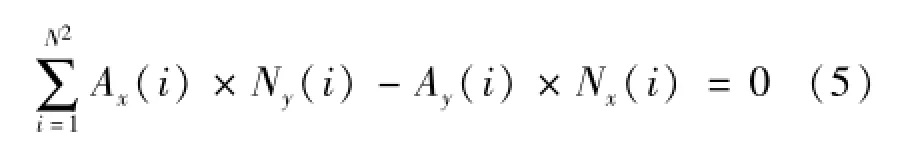
式中:N为方形栅格板一列点的个数;i为总测量点数,即标记点数,i=1,2,…,N2。
2.2 数学模型
辅助测量栅格板固定在二维平面工作台上,通过精密仪器测得栅格板上标记点i的坐标测量值,记为Mx(i)和My(i)。根据图2中向量之间的关系,有
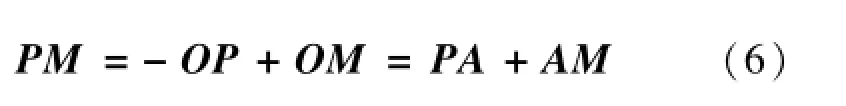
写成矩阵形式可得:


根据式(1)~(8),可以得到误差分离的数学模型:

式中:Qx为测量值在X轴方向的分量;Qy为测量值在Y轴方向的分量;I为N2阶单位矩阵;Ic为元素均为1的单列矩阵;o为零矩阵;Nx、Ny均为N2列单行矩阵,其元素为标记点的标称值,符号依据坐标系而定;[·]T表示转置矩阵。
式(9)是1个位置的情况,方程中的未知量为4N2+3个,已知量为2N2+7个。通常N≥2,未知量的个数大于已知量的个数,方程的解不定。为了得到可靠的估计值,应使已知量的个数大于未知量的个数,所以需要增加位置数。结合数学模型采用平移、旋转等不同位置来获得多组测量数据,如图3所示,其中虚线表示理想栅格板,实线表示辅助栅格板,圆点表示标记点。
对于3位置的数学模型,方程中的未知量为4N2+9个,已知量为6N2-2N+7个,已可保证已知量的个数大于未知量的个数。为了得到最佳估计值,本文采用最小二乘法对数据进行处理。
根据图3所示不同位置标记点坐标值的变化,由式(9)可得到3位置时的误差分离数学模型:

式中:上标1、2、3表示测量位置;I90为顺时针旋转90°后对应的系数矩阵;Id、Ie、If、Nf、Ng均为栅格板向x轴正向平移一个栅格后所产生的系数矩阵;其他矩阵意义同式(9)。

图3 误差分离3位置示意图
式(10)左侧为已知量,简记为Q,右侧的关系矩阵记为T,最右侧一列为待分离量,简记为X。于是,式(10)可改写为:

根据式(11),利用最小二乘公式:
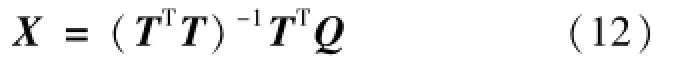
可得到误差分离结果的最佳估计值为:
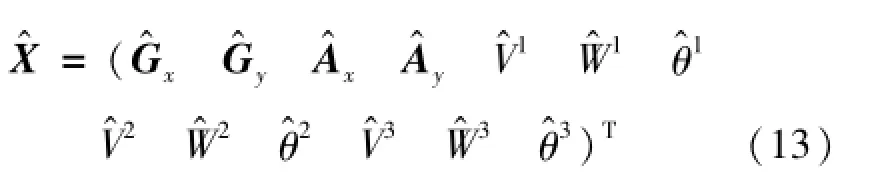
式(13)即为待分离的所有误差项的计算结果,即最佳估计值。可见,该误差分离方法能将二维工作台的系统误差分离出来。
3 仿真分析
为了验证该误差分离算法的有效性进行了计算机仿真。仿真流程如图4所示。辅助测量栅格板标记点为4×4,即N=4,相邻两个标记点间距d为10 mm。根据上文提到的条件即式(1)~(5),随机生成测量数据、工作台、辅助测量栅格板的系统误差数据。设置工作台测量点和栅格板标记点的系统误差标准差均为0.1μm。经过最小二乘法计算,得到测量数据中包含的测量点系统误差和标记点系统误差以及偏移量。通过标准差和标准不确定度来比较与给定值的偏差。
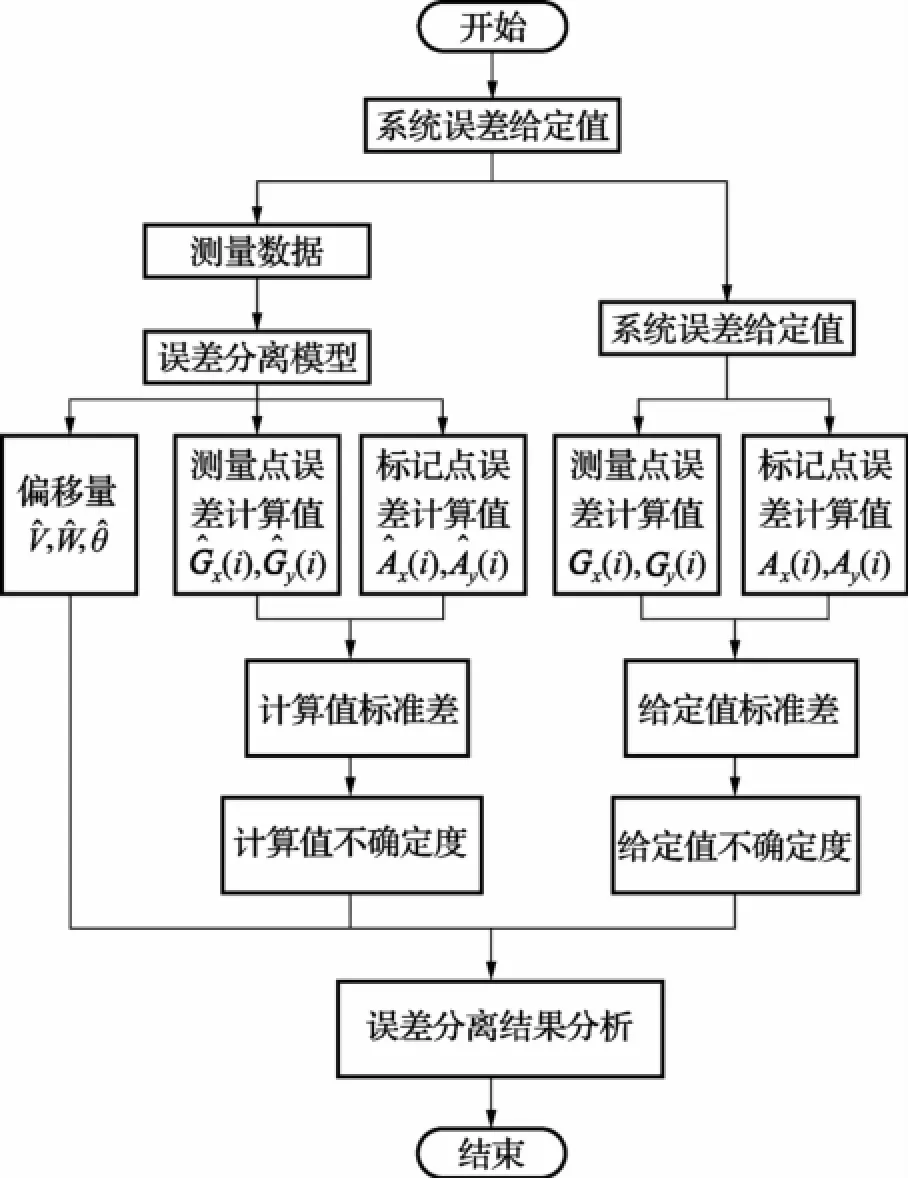
图4 仿真流程图
考虑到实际测量环境中无法避免外界的干扰,即存在随机误差的影响,在仿真过程中针对有、无随机噪声两种情况进行了误差分离。
3.1 无随机噪声的情况
当无随机噪声时,误差分离计算值与给定值相同,如图5所示,圆点表示计算值得到的标记点位置,虚线表示计算值和给定值无偏差,实线表示计算值和给定值的偏差。在无随机噪声影响的情况下,对于每个工作台测量点和栅格板标记点,误差给定值与计算值相同,该算法能完全分离出二者的系统误差。
3.2 有随机噪声的情况
当加入随机噪声时(本文取随机噪声的幅度为0.1 000μm),测量数据经利用误差分离算法处理后,得到的误差给定值与计算值数据如表1所示,两者的误差偏离如图6所示,其中圆点表示计算值得到的标记点位置,虚线表示计算值和给定值无偏差,实线表示计算值和给定值的偏差。

图5 无随机噪声时的仿真结果

表1 有随机噪声时的误差给定值与计算值μm

图6 有随机噪声仿真结果
由表1和图6可以看出,在有随机噪声的情况下,工作台测量点误差分离结果与给定值虽有偏差,但其标准差的相对误差在X轴和Y轴分别为1.95%和1.52%,如表2所示。

表2 有随机噪声时的标准差和标准不确定度
由于在实际操作中,噪声对测量结果有一定的影响,为了验证该算法对噪声的抑制能力,对噪声参数给出具体的数值,根据噪声大小的不同,仿真结果,如表3所示。噪声与工作台的系统误差相比,前者在数量级上明显小于后者,因此选取噪声幅度0.100 0μm作为上限。从表3可以看出,随着噪声数量级上的增大,计算值与给定值的标准差并没有随之而增大,在一个很小的范围内波动,比较稳定,即该算法对噪声有抑制能力,表现出较好的鲁棒性。

表3 不同噪声参数的仿真结果比较μm
4 结 论
本文提出一种精密仪器二维精密工作台离散点测量结果误差分离的新方法,建立了误差分离数学模型,并对算法进行了仿真验证。仿真结果表明:当无随机噪声存在时,该算法能够实现误差的完全分离;当加入幅度为0.100 0μm的随机噪声时,系统误差的计算值和给定值的标准差的相对误差在X轴和Y轴分别为1.95%和1.52%。该方法既可用于测量设备的性能评价,也能够用于测量结果的修正,从而得到更准确的测量结果。
[1] 青木保雄,大园成夫.三点法真圆度测定法の展开[J].精密机械,1966,32(12):27-32.
[2] 张雷,赵莹,张玉.三测头法误差分离技术的理论与试验[J].机械工程学报,2009,45(6):256-261.
[3] 韩正铜,洪迈生.圆度误差分离的三点法及其演化形式与精度分析[J].机械设计与制造,2002,(2):54-55.
[4] 杨洪寿,费业泰,陈晓怀,等.纳米三坐标测量机的误差分析与分离[J].安徽理工大学学报,2010,30(3):36-40.
[5] Ye J,Takac M T,Berglund C N,etal.An exact algorithm for self-calibration of precision metrology stages[J].PrecisionEngineering,1997,20(1):16-32.
[6] Raugh M R.Absolute two-dimensional sub-micron metrology for electron beam lithograph[J].Precision Engineering,1985,7(1):3-13.
[7] Takac M T,Ye J,Pease R F,etal.Self-calibration in two dimensions:the experiment[J].SPIEDigital Library,1996,2725:130-146.
[8] 朱煜,朱立伟,尹文生,等.IC加工及检测装备超精密工作台自标定技术研究[J].电子工业专用设备,2005,34(3):20-24.
[9] 朱立伟,朱煜,尹文生.超精密二维工作台自标定技术研究[J].中国机械工程,2005,16(20):1787-1890.
[10] Zhu Y,Hu C X,Hu J C.Least-square based selfcalibration of two-dimensional ultra-precision stages[C]//2011 International Conference on Mechatronics and Automation(ICMA),Beijing,China.2011:597-602.
[11] Zhu Y,Hu C X,Hu JC.A transitive algorithm for selfcalibration of two-dimensional ultra-precision stages[C]//International Conference on Advanced Intelligent Mechatronics(AIM),Budapest,Hungary.2011:594-598.
[12] Hu C X,Zhu Y,Hu J C,etal.A holistic selfcalibration approach for determ ination of threedimensional stage error[J].Transactionson InstrumentationandMeasurement,2013,62(2):483-494.
[13] 崔继文,刘雪明,谭久彬.超精密级二维工作台的自标定[J].光学精密工程,2012,20(9):1960-1966.
A New Error Separation Method for Measurement Results of Discrete Points of 2D Precision Stage
GUO Tian-tai1, WANG Xiao-xiao1, HONG Bo1, ZHAO Jun1, KONG Ming1, GAO Si-tian2
(1.China Jiliang University,Hangzhou,Zhejiang 310018,China;2.National Institute of Metrology,Beijing 100013,China)
To separate the system error of precision stage,a new method for separation was put forward.Firstly different positions of auxiliarymeasuring grid plate and 2D-stageweremeasured.Then according to themeasurement data of mark points on the grid plate and their corresponding nominal values,a mathematical model for error separation was established,which could separate errors from themeasured results.The effectiveness of the algorithm was verified through simulation.Simulation results showed thatwhen therewas nomeasurementnoise,the algorithm could realize completeerror separation,while in the case of the presence ofmeasurement noise,the relative error of standard deviation of calculated values and the given values were 1.95%and 1.52%inX-axis andY-axis respectively.For noises with different amplitudes,the calculated values of system errorswere stable.The algorithm is not sensitive to noise and can be very useful in evaluation ofmeasurement results and instrument performances.
Metrology;Error separation;2D precision stage;System error;Measurement results;Uncertainty
TB92
A
1000-1158(2014)02-0113-07
10.3969/j.issn.1000-1158.2014.02.04
2013-05-10;
2013-07-25
国家自然科学基金(11172287);国家重大科学仪器设备开发专项(2011YQ03011208)
郭天太(1968-),男,甘肃庄浪人,中国计量学院副教授,博士。主要研究方向为精密仪器与现代传感技术。teampaper209@cjlu.edu.cn

