全张量重力梯度数据误差分析及补偿
袁 园,黄大年,余青露,耿美霞
1.吉林大学地球探测科学与技术学院,长春 130026
2.中国石化石油物探技术研究院,南京 211103
0 前言
近20年来,高精度重力梯度探测技术被广泛应用于区域和局部地球物理勘探中,联合地震等勘探手段提高了对探测对象进行精确解释的能力。该项技术通过航空和船载方式成功地应用于能源和矿产资源勘查,为重新认识重力勘探方法技术提供了依据。美国墨西哥湾深海油田勘探开发以及内陆大型推覆体构造下油气田和矿床的发现,都与该项技术的应用有关。在国防领域,该数据可用于移动条件下的精确导航定位和发现地下或水下隐伏目标。我国正着力于探测关键技术装备的研发[1]。目前,国际上正在研制和发展的航空和船载快速移动测量条件下的重力梯度仪包括旋转加速度计重力梯度仪、超导重力梯度仪、冷原子重力梯度仪等。成功投入勘探应用的重力梯度仪只有基于美国Lockheed Martin公司研制的旋转加速度计全张量重力梯度仪 (FTG,包 括 3 个 GGI(gravity gradiometer instrument))、在此基础上发展的澳大利亚BHP公司Falcon水平张量航空重力梯度仪和Bell Geospace(现在的 Lockheed Martin)研制的 Air-FTGTM与为ARKeX公司研制的FTGeX全张量重力梯度仪。这3种重力梯度仪都是基于旋转加速度计的设计原理[2]。其中,Air-FTGTM经过不断完善探测精度已达到8E①厄(E)为非法定计量单位,1E=10-9 s-2,下同。,仪器敏感度(即噪声水平)达11E/[3],FTGeX 全张量重力梯度仪达7E/[4]。
鉴于该项技术的广泛用途和效率,国内学者一直关注该项技术的发展,近年来已经开展了对FTG应用原理和核心技术的研究。罗嗣成[5]和李海兵等[6-7]对全张量重力梯度仪进行了静态环境下的误差分析。涂良成等[8]对仪器设计敏感度达1E/的高精度全张量重力梯度仪进行了加速度计的性能匹配分析,指出单项加速度计的标量因子一致性匹配需达10-11量级,二阶非线性系数调节需要达到10-11g/g2的量级。如此超高精度的技术要求往往受到工业制造能力的限制,构成了必须突破的技术瓶颈。目前,国内市场上可获取的加速度计敏感度只能达到10-7g(g为重力加速度)。因此,为了达到加速度计高精度要求,一些改进措施应运而生。O’Keefe等[9]和 Metzger等[10]提出了加速度计的反馈实时调节,以实现加速度计之间的动态匹配来降低在组合形成FTG过程中所固有噪声水平。为获取高精度重力梯度测量数据,满足矿产勘查的精度要求,还需要对FTG测量值进行外界干扰误差分析并去除其影响。在航空测量条件下,袁园[11]对比分析了对随机噪声的常用滤波方法。除此之外,最主要的干扰是飞行姿态变化(如俯仰角、偏航角、滚转角)引起的重力梯度环境变化。笔者针对该影响,从理论分析角度提出采用点源质量进行机身环境梯度校正的快速补偿方法。
1 全张量重力梯度仪测量原理
1.1 坐标系的定义
航空重力梯度测量系统中包含了5个坐标系统:惯性坐标系xiyizi(i系)、导航坐标系xnynzn(n系)、飞机自身坐标系xbybzb(b系)、加速度计坐标系oaiapa(a系)和梯度仪坐标系xgygzg(g系)。加速度计的定义见图1:与圆盘相切的轴为加速度计的感应轴ia,圆盘法线方向为oa,垂直于圆盘方向为pa。梯度仪坐标系(g系)定义为:与惯性坐标系对齐,坐标原点og位于圆盘圆心,xg与xi对齐,yg与yi对齐,zg与zi对齐。
1.2 全张量重力梯度仪的构造
FTG系统由3个旋转重力梯度圆盘装置GGI组成,采用伞形结构。3个圆盘的旋转轴俯视夹角为120°,水平夹角约为35°[12]。也有采用垂直夹角方式结构形成FTG组合[13](图2)。两者可取得相同的测量结果,笔者按后者展开讨论。FTG系统每个圆盘平面的轴与g系的一个轴平行,如xgyg面上圆盘的轴与zg轴平行,4个三轴加速度计的验证质量中心到圆盘中心的距离相等,相邻2个加速度计的相位间隔为90°(图2)。第j加速度计的坐标系统为a系oajiajpaj,加速度计的输出轴iaj轴正切于圆盘,加速度计1与2的敏感轴方向相反,加速度计3与4的敏感轴方向相反,两对加速度计垂直安装。
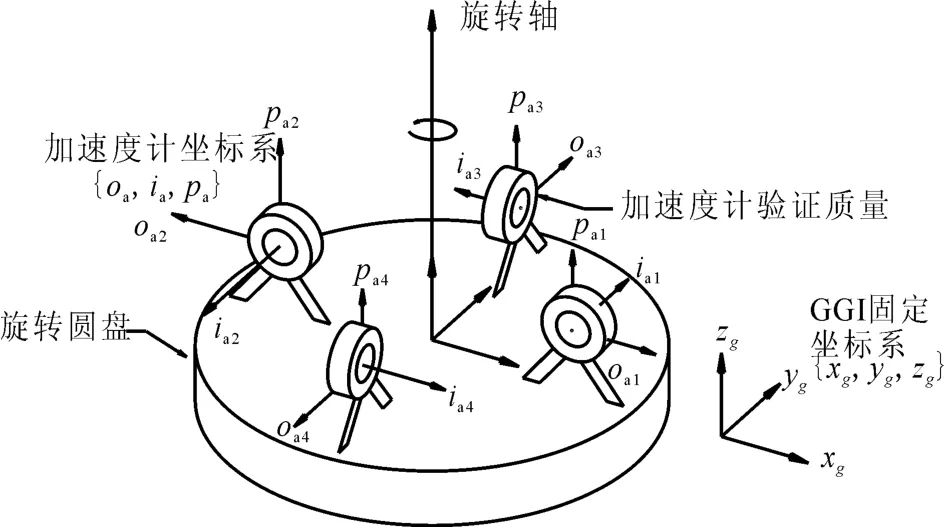
图1 单个GGI圆盘安装的三轴加速度计[10]Fig.1 3-aixs accelerometer triad on a GGI[10]

图2 全张量重力梯度仪构造[10]Fig.2 Structure of FTG[10]
1.3 全张量重力梯度仪测量方程
在勘探测量过程中,Richeson[14]和Jekeli[15]分别给出了移动载体在加速度计坐标系下的运动加速度表达式:
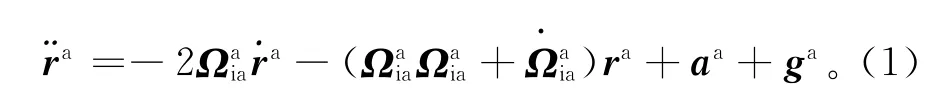
式中:ra为加速度计的位移;ra为位移的一阶导数;aa为加速度计在a系下测得的比力;ga为a系下的重力加速度;Ωaia为a系下a系相对于i系的旋转角速度waia=[wx,wy,wz]T各元素组成的斜对称矩阵[2];Ω·aia为相应的角加速度˙waia=[˙wx,˙wy,˙wz]T组成的斜对称矩阵。

根据式(1)可得到移动平台中每个三轴加速度计在a系下测量的比力由4部分组成:
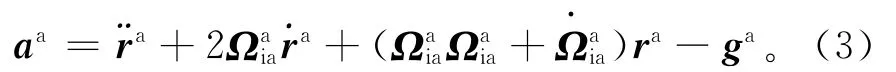
式中:右边第一项为载体在a系下的运动加速度;第二项为物体在旋转坐标系中由速度引起的科里奥利加速度;第三项中括号里的第一项为加速度计旋转受到的离心加速度,第二项为坐标受到的角加速度影响;最后一项为a系下的重力加速度。
在式(1)和式(3)的基础上,根据GGI工作原理推导出重力梯度测量方程的表达形式。FTG测量采用的3个GGI均具有相同的构造,仅安装方向不同。对单一GGI而言,GGI旋转圆盘中有4个加速度计对称安置(图2)。每对加速度计之间的距离可表示为
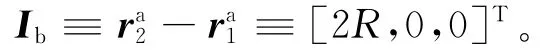
式中:ra1和ra2分别为加速度计a1和a2的位移;R为加速度计到圆盘中心的距离,一般为0.1m。注意到Ib的一阶导数和二阶导数为零,˙Ib=¨Ib=0,则每个加速度计感受到的旋转角速度和角加速度作用力相同。利用此特点可得每对加速度计的测量输出:
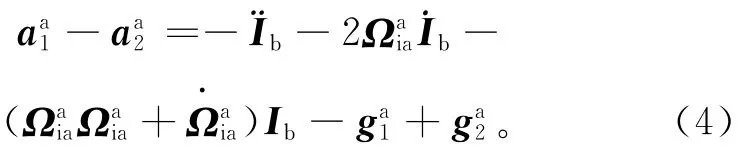
式中:aa1、aa2为加速度计a1、a2的测量值;ga1、ga2为加速度计a1、a2安装位置处的重力加速度。由于每对加速度计置放的微小距离(厘米级)引起的重力梯度变化很小,可忽略非线性高阶项部分对分析结果的影响[4],选择每对加速度计差值的线性项作为研究梯度的表达式:

将式(5)带入式(4),得
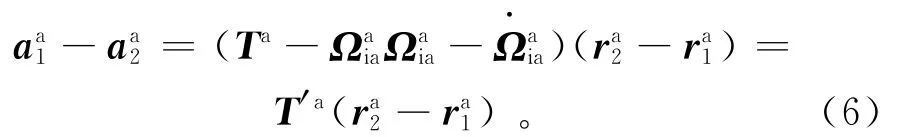
式中:Ta为需要测量重力梯度张量矩阵;T′a为GGI直接测量的重力梯度张量矩阵。
GGI在移动测量条件下,某一时刻的梯度测量值为
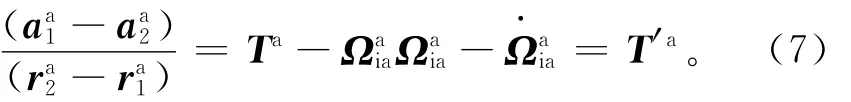
式(7)表明,GGI测量值除了对所需重力梯度的直接测量(即Ta)外,还包含了需要消除的离心加速度(ΩiaaΩiaa)和角加速度()的影响。
此外,对梯度测量值的影响还包括a系中加速度计参数的影响。三轴加速度计测量了o、i、p3个方向上的加速度,即a=[a0,ai,ap]。每个三轴加速度只有一个感应输出轴i,垂直于感应轴i方向上的加速度不能被输出[10],输出信号为正弦变化的模拟电流和电压信号,为3个方向上加速度的二阶多项式组合输出形式。所以,三轴加速度计的输出模型[4,6,11]为
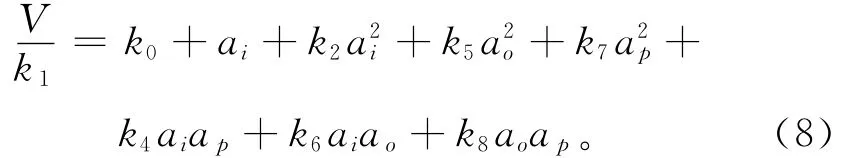

其中:wx和wy为圆盘水平方向上的旋转速率;wz为圆盘的正常旋转速率;a系相对于g系在xgyg平面上没有角运动,即wx=wy=0。设单个GGI中第j个加速度计的输出为Vj。理想情况下,各加速度计性能应该完全匹配和完全对齐安装在稳定的平台上。Richeson[14]推导了单个GGI的理想输出表达式:
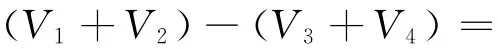
式中:V、k1、k0分别为加速度计的输出电压、偏差和标量因子;k2、k5、k7分别为加速度计在o、i、p3个方向上的二阶非线性系数;k4、k6、k8分别为3个方向上交叉耦合项的二阶非线性系数。
由于每个GGI都被安装在同一平台上,所以梯度仪坐标系g与惯性坐标系i重叠,导致加速度计坐标系相对于惯性坐标系的旋转速率与相对于梯度仪坐标系的旋转速率相等,即
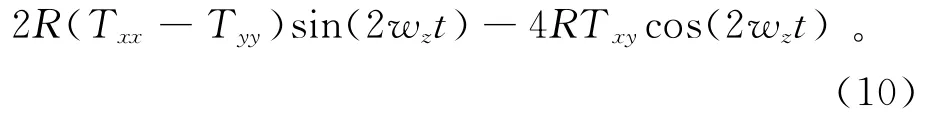
式中:V1、V2、V3、V4分别为加速度计a1、a2、a3、a4的输出电压;Txx、Tyy和Txy为重力梯度量。式(10)说明,理想输出结果经过2wz信号调制可得到3个梯度量的2个组合输出(Txx-Tyy)和Txy。同理,对其他2个GGI分析,可以分别得到另外2组梯度信号的组合输出:(Tyy-Tzz)和Tyz;(Tzz-Txx)和Tzx。3组梯度信号经整理可构成测量所需的3×3FTG测量系统,即
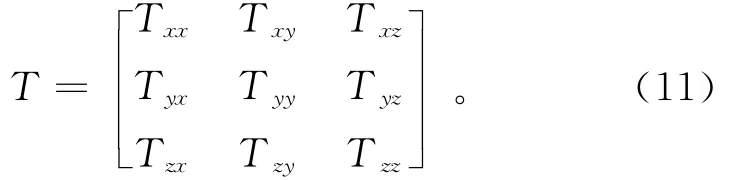
2 FTG误差分析
式(11)中含有测量误差,包含GGI安装误差和研制误差。原因是实际测量中难以满足理想输出条件。罗嗣成[5]和李海兵等[6]对安装误差进行了系统分析,认为该误差可以控制和消除。笔者主要从各加速度计性能和匹配程度来分析GGI的固有误差。式(3)说明加速度计测量的比力受到平台角速度和角加速度的影响;式(8)说明加速度计的输出受到加速度计性能参数的影响。所以,造成全张量重力梯度仪误差的原因主要有:加速度计性能参数不匹配,圆盘旋转速度的不稳定和平台的不稳定,三者形成相互制约的影响关系。
2.1 加速度计标量因子和偏差不匹配影响分析
令式(8)的二阶非线性系数为零,即k2=k5=k7=k4=k6=k8=0,联合式(3),可推导出GGI在加速度计标量因子和偏差不匹配、圆盘旋转角加速度和平台不稳定情况下的实际测量值为


2.2 加速度计二阶非线性系数不匹配影响分析
上述分析结果可扩展到当加速度计二阶非线性系数不为零时对GGI测量值产生的影响。假设在GGI圆盘中4个加速度计标量因子和偏差完全匹配,同时所安装平台稳定和圆盘转速稳定,在此情况下分析仅由加速度计二阶非线性系数不匹配产生的误差。设各加速度计的偏差为0,标量因子为k1。联合式(3)和式(7),可得到4个加速度计的二阶非线性系数与GGI圆盘中心的运动加速度和重力加速度产生的2倍频误差表达式:
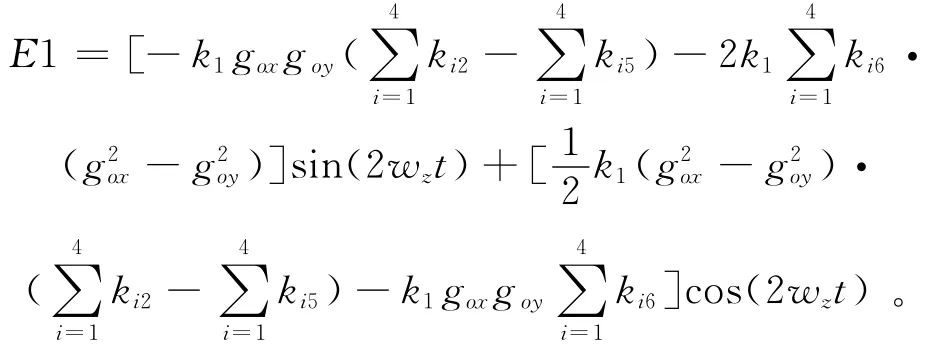
式中:下标i表示4个加速度计a1、a2、a3和a4。该表达式再次表明由此产生了与cos(2wzt)和sin(2wzt)有关的噪声信号。
2.3 Simulink仿真
为验证上述理论分析结果,可利用Simulink仿真系统工具建立FTG测量值固有噪声分析系统,分别对加速度计性能参数不匹配、圆盘旋转速度的不稳定、平台不稳定的影响因素进行分析。GGI圆盘的旋转周期为4s,半径为0.1m。因为FTG中3个GGI的结构完全相同,所以,在仿真过程中对FTG中的3个GGI采用相同的仿真实验参数。王新龙等[16]给出了当加速度计精度为10-7g时的模型参数,见表1。O’Keefe等[9]给出了圆盘旋转参数:wx=30×10-5rad/s,wy=30×10-5rad/s,wz=0.50πrad/s,˙wz=0.25cos(2wzt)rad/s2。图3表明,当加速度计的精度为10-7g时,旋转平台不稳定和加速度计标量因子至少能够引起几十厄幅值的噪声,平台旋转速率不稳定也可引起数厄幅值的噪声。图4表明,加速度计二阶非线性系数不匹配引起的噪声幅值最大能达到106E,将完全淹没和扭曲实际的梯度值。

表1 GGI圆盘4个加速度计模型系数(精度为10-7 g)Table 1 Parameters of four accelerometers install on GGI platform (the precision is 10-7 g)

图3 全张量重力梯度仪中3个GGI在只考虑标量因子和偏差不匹配,平台不稳定和圆盘旋转速率不稳定时的测量误差Fig.3 Measurement error caused by mismatch of accelerators’scale factors and bias error,platform instability and disc rotating speed unstable of three GGI in FTG

图4 全张量重力梯度仪中3个GGI在只考虑各加速度计二阶非线性系数不匹配时的测量误差Fig.4 Measurement error caused by mismatch of accelerometers of second order nonlinear coefficients of three GGI in FTG
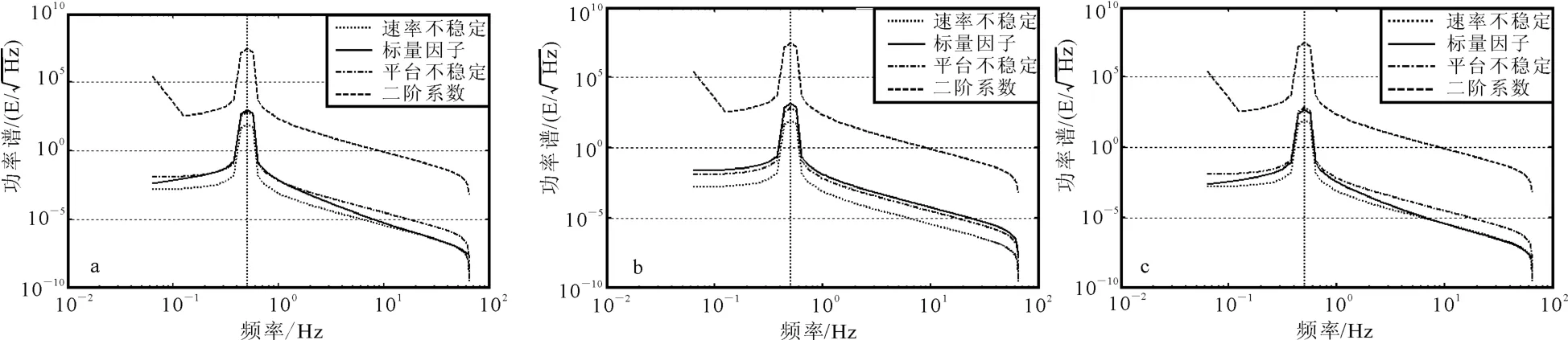
图5 全张量重力梯度仪中3个GGI的噪声影响因子的功率谱噪声水平Fig.5 Power spectral density noise levels of each error mechanism of three GGI in FTG
2.4 FTG固有噪声水平
可以利用频率域能量分析衡量导致FTG测量误差的3个关键因素——加速度计参数不匹配、圆盘转速不稳定和平台不稳定,来确定3个误差来源对测量噪声的干扰程度。图5为Simulink仿真各误差项的功率谱,解调频率为0.5Hz。由图5可见,所有项在0.5Hz处的功率谱最大,确定该处的能量为所估计的噪声水平。从图5中还可看出:由标量因子、不稳定平台产生的噪声水平为103E/;由平台旋转速率不稳定性产生的噪声水平约为102E/;由二阶非线性系数引起的噪声水平为2.9×107E/。这些噪声项将严重影响FTG系统的整体精度。为此,笔者在研制FTG时,要求足够匹配的加速度计、足够稳定的平台以及足够稳定的转速来提高FTG最终测量精度。
为了获取FTG高精度测量数据,必须采取措施去除或压制各误差项。O’Keefe等[9]对于加速度计不够匹配造成的噪声,通过实时反馈系统在线调节的方法对其标量因子和二阶非线性系数进行补偿,实现多个加速度计标量系数闭环微调,达到一致。反馈调节主要是通过改变磁感应强度B来调节加速度计的标量系数[17-18]。对于平台不稳定造成的误差,通过设计三轴陀螺稳定平台,使重力梯度仪不随载体姿态的改变而发生变化,保持在水平方向上没有旋转角速度[19]。而对旋转速度不稳定情况,对圆盘添加一个与设计要求相近的旋转速率wz2,这样将增加测量信号的带宽,同时可以对wz2频率成分进行实时监测,实时调节振幅信号中标量因子的不匹配,从而通过在线调节标量因子的方法达到要求[5,7]。上述努力在实验中已验证是行之有效的。但是,在去除FTG测量值内部干扰误差的同时还需从外部影响角度考虑去除方法。
3 测量环境自身梯度校正
3.1 飞行姿态变化产生的梯度改变
全张量重力梯度仪周围质量分布产生的测量环境对自身梯度影响,将随着飞行姿态的变化而变化[19]。实际测量中,飞机运动姿态呈多样化,使得飞机自身坐标系b相对于地理坐标系n的位置关系发生改变。可以通过飞机的俯仰角、偏航角、滚转角记录来描述飞机姿态变化情况。FTG系统中的三轴陀螺稳定平台使得梯度仪不随飞机飞行姿态角的改变而在空间上发生位置变化。即当飞机绕着任何轴旋转时,梯度仪在空间保持方向不变。因此,飞机相对于梯度仪的旋转,改变了梯度仪的周围质量的空间分布,从而改变了周围质量引起的自身梯度。
另外,FTG周围主要的质量分布有引擎、飞行员、燃油和其他的辅助测量仪器DGPS、雷达测高计等。由于DGPS和雷达测高计等的质量太小,对重力梯度基本不造成影响,因此,一种简单的分析方法是将影响重力梯度的质量体当作点源。
飞机中全张量重力梯度仪附近的一个质量为M的物体在b坐标系中的位置坐标为(xb,yb,zb),在导航坐标系(n系)下的位置坐标为(xn,yn,zn)。当飞机自身坐标系b发生变化时,b系到n系的方向余弦矩阵Cnb也将变化,2个不同时刻m1、m2对应的方向余弦矩阵为Cnbm1,Cnbm2,则M在n系m1、m2时刻的位置坐标分别为
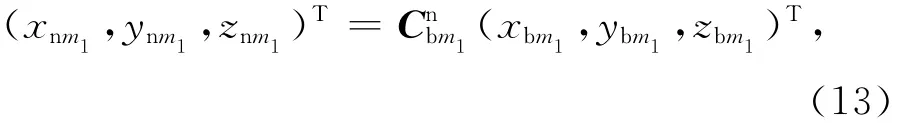
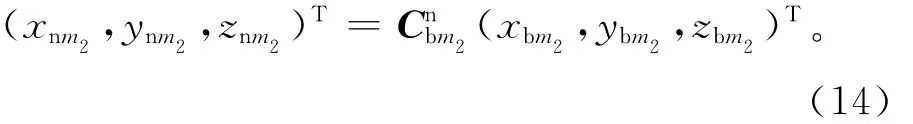
根据物体M相对梯度仪的位置,在n系中全张量重力梯度仪测得的由M引起的重力梯度为

其中:r=;G为万有引力常数。根据物体M在n系中不同时刻的位置关系,即可求得各时刻的梯度校正量,以及自身梯度的改变量ΔTij(i和j表示x,y和z)。表2给出了飞机姿态角改变量为10°、燃油质量为1 200kg时各梯度的改变量。可以看出,姿态改变引起自身梯度的最大改变量超过2E。为了得到高精度的重力梯度测量值,需实时监测飞行姿态,以便准确地进行自身梯度校正,且经这种方法得到的改变量满足拉普拉斯方程,即


表2 按点源计算方法得出的燃油质量1 200kg在姿态角改变10°时的自身梯度的改变量Table 2 Change of self-gradient caused by fuel mass 1 200kg when attitude angle changed 10° E
3.2 飞机自身质量变化产生的梯度改变
随着勘探的进行,由于燃料的消耗,体积不断减少,燃料质量引起的自身梯度的校正量不但与飞行姿态和梯度仪质心位置有关,还是与时间相关的函数。
燃油的密度不是一个恒定不变的值,它会随着飞机飞行高度、大气压力以及分布在飞机各部位的油箱(主油箱、辅助油箱)温度变化而改变[20]。另外,环境压力及温度的变化对密度的影响也比较复杂。也就是说,当飞机处于不同环境时,其油箱中燃油的密度是不同的。所以,为了得到高精度的梯度值,燃油质量的实时监测是非常必要的。质量的变化并不是随时间的简单线性变换。这里先忽略飞行高度、大气压力、温度等对密度的影响,视质量与时间为简单的线性关系。以Cessna Grand Caravan 208飞机为例,飞机的续航能力为6h,燃油载重1 200kg。假设飞机按照预先设计的路线平稳飞行,则由燃油质量随时间的变化引起的自身梯度的变化如图6所示,由燃油产生的自身梯度值从开始的最大10E逐渐趋于零。因此,需要实时监测燃油质量,以对自身梯度随质量的变化进行补偿。
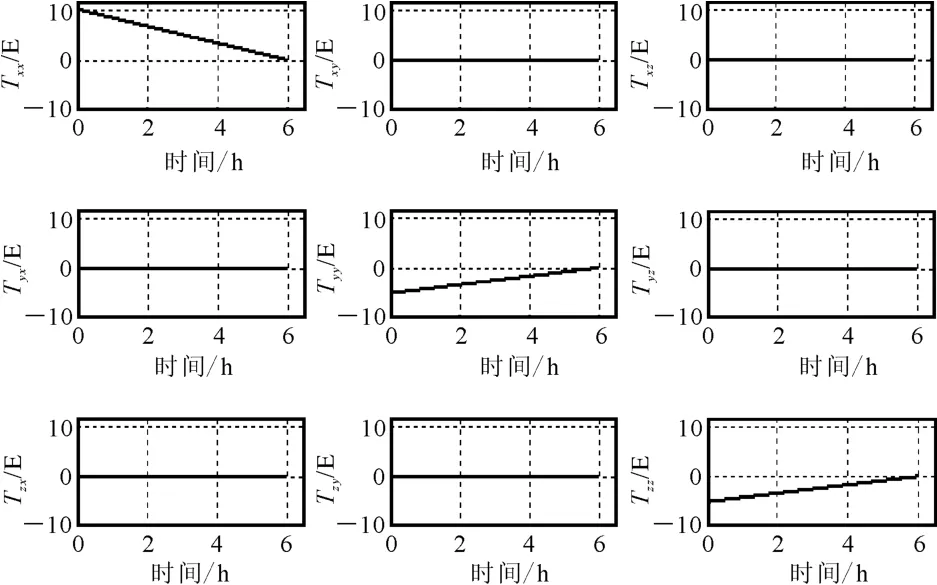
图6 按点源计算方法确定的飞机燃油随时间和消耗引起的自身梯度的变化及校正量Fig.6 Changing of fuel self-gradient along with time calculated by point mass method
实际自身梯度校正过程中,需联合自身梯度随飞行姿态和质量的变化进行综合校正。笔者提出的基于点质量源的校正方法是对质量体的一个近似,目的是为了快速进行自身梯度校正,是一种近似校正方法。
4 结语
本文从移动平台测量的动态环境出发,推导了全张量重力梯度仪在动态环境下的测量方程,分析了影响测量值的固有噪声的影响因素。利用Simulink建立的仿真模型分析了各影响因素产生的固有噪声的幅值和噪声水平,以确定其对固有噪声的贡献水平。试验结果显示:标量因子及平台不稳定都能引起至少几十厄的测量误差,噪声水平约为103E/;而二阶非线性系数能产生106E的测量误差,噪声水平为2.9×107E/,这将完全淹没真实梯度值。同时,这些影响可以通过采取适当措施予以压制和克服。最后,为了得到高精度的航空重力梯度值,分析了外界干扰梯度测量值,推导了飞机自身梯度校正的点源计算方法,对随着飞行姿态和质量不断改变的自身梯度进行了校正。
(
):
[1]黄大年,于平,底青云,等.地球深部探测关键技术装备研发现状及趋势[J].吉林大学学报:地球科学版,2012,42(5):1485-1496.
Huang Danian, Yu Ping, Di Qingyun,et al.Development of Key Instruments and Technologies of Deep Exploration Today and Tomorrow[J].Journal of Jilin University:Earth Science Edition,2012,42(5):1485-1496.
[2]DiFrancesco D,Grierson A,Kaputa A,et al.Gravity Gradiometer Systems:Advances and Challenges[J].Geophysical Prospecting,2009,57(4):615-623.
[3]Murphy C A.Recent Developments with Air-FTG[C ]//ASEG-PESA Airborne Gravity 2010 Workshop.[S.l.]:Geoscience Australia,2010:142-151.
[4]Houghton P,Lumley J,Barnes G,et al.A Comparison
of Three Current Airborne Systems Designed to Measure the Earth’s Gravitational Field and the Impact of Instrument Sensitivity on Mining Exploration[C]//SAGA-AEM 2004Conference.[S.l.]:South African Geophysical Association,2004.
[5]罗嗣成.旋转加速度计重力梯度仪[D].武汉:华中科技大学,2007.
Luo Sicheng.Rotating Accelerometer Gravity Gradiometer[D].Wuhan:Huazhong University of Science and Technology,2007.
[6]李海兵,蔡体菁.旋转加速度计重力梯度仪误差分析[J].中国惯性技术学报,2009,17(5):525-528.
Li Haibing,Cai Tijing.Error Analysis on Gravity Gradiometer of Rotating Accelerometer[J].Journal of Chinese Inertial Technology,2009,17(5):525-528.
[7]李海兵,蔡体菁.全张量重力梯度仪测量方程及误差分析[J].东南大学学报:自然科学版,2010,40(3):517-521.
Li Haibing,Cai Tijing.Measurement Equations and Error Analysis of Full Tensor Gravity Gradiometer[J].Journal of Southeast University:Natural Science Edition,2010,40(3):517-521.
[8]涂良成,刘金全,王志伟,等.旋转重力梯度仪的加速度计动态调节方法与需求分析[J].中国惯性技术学报,2011,19(2):131-135.
Tu Liangcheng,Liu Jinquan,Wang Zhiwei,et al.Methods and Requirements of Dynamic Compensation Between Accelerometers in Rotating Gravity Gradiometer [J]. Journal of Chinese Inertial Technology,2011,19(2):131-135.
[9]O’Keefe G J,Lee J B,Turner R J,et al.Gravity Gradiometer:US,5922951[P].1999-07-13.
[10]Metzger T,Sieracki D L,Dosch D E.Gravity Gradiometer System:US,0064778A1[P].2009-03-12.
[11]袁园.航空重力数据常用滤波方法对比研究[J].吉林大学学报:地球科学版,2010,40(增刊):6-10.
Yuan Yuan.Comparative Study of Common Filtering Methods Used in Airborne Gravity Data[J].Journal of Jilin University:Earth Science Edition,2010,40(Sup.):6-10.
[12]Brett J.Theory of FTG Measurements[EB/OL].[2011-09-20].http://www.bellgeo.com.
[13]Hofmeyer G M,Affeck C A.Rotating Accelerometer Gradiometer:US,5357802[P].1994-12-25.
[14]Richeson J A.Gravity Gradiometer Aided Inertial Navigation Within Non-GNSS Environments[D].Maryland:University of Maryland,2008.
[15]Jekeli C.Airborne Gradiometry Error Analysis[J].Surveys in Geophysics,2006,27(2):257-275.
[16]王新龙,申功勋,何乃刚.一种有效的加速度计静态模型辨识方法[J].仪器仪表学报,2003,24(1):57-60.
Wang Xinlong,Shen Gongxun,He Naigang.An Efficient Discrimination Method of the Accelerometer Static Model Parameters[J].Chinese Journal of Scientific Instrument,2003,24(1):57-60.
[17]聂鲁燕,刘晓东,宋超,等.重力梯度仪旋转加速度计标度因数匹配方法[J].中国惯性技术学报,2010,18(5):533-537.
Nie Luyan,Liu Xiaodong,Song Chao,et al.Scale Factor Matching Method for Rotating Accelerometers of Gravity Gradiometer[J].Journal of Chinese Inertial Technology,2010,18(5):533-537.
[18]杨功流,刘洋希,李晓平.重力梯度仪加速度计控制回路分析与设计[J].中国惯性技术学报,2009,17(2):145-152.
Yang Gongliu,Liu Yangxi,Li Xiaoping.Analysis and Design on Control Loops of Gravity Gradiometer Accelerometer[J].Journal of Chinese Inertial Technology,2009,17(2):145-152.
[19]Lee J B,Falcon Gravity Gradiometer Technology[J].Exploration Geophysics,2001,32(3):247-250.
[20]李楠,吕俊芳.飞机燃油密度实时测量及其实现方法[J].计测技术,2002,22(1):24-26.
Li Nan,LüJunfang.Real Time Measurement and Its Method of Aircrafts Fuel Density[J].Metrology &Measurement Technology,2002,22(1):24-26.

