高速铁路CP0基线解算中起算点坐标精度研究
周东卫
(中铁第一勘察设计院集团有限公司,西安 710043)
高速铁路CP0基线解算中起算点坐标精度研究
周东卫
(中铁第一勘察设计院集团有限公司,西安 710043)
在高速铁路CP0基线解算过程中,需要将IGS参考站作为起算点,当起算点坐标出现误差或兼容性较差时,将导致整个框架控制网基线向量解产生系统性旋转和尺度变化,因此必须对起算点坐标的允许精度进行研究。介绍起算点误差传播与影响模型,从理论上分析起算点误差对基线解算的影响程度,通过设计不同解算方案采用工程测量数据对起算点坐标的允许精度进行研究。结果表明,使用GAMIT软件进行CP0框架控制网解算时必须严格控制起算点坐标的误差,起算点点位坐标精度最好控制在10 cm之内;当起算点坐标误差达到20 cm时,各基线分量的解算结果的精度在毫米级的量级;当起算点坐标误差达到2 m时,基线解算结果不可靠,不满足高精度解算要求。
高速铁路;GPS;起算点;框架控制网;IGS参考站;精度
1 概述
高速铁路线路长、地区跨越幅度大且平面控制网沿线路呈带状布设,为了控制带状控制网的横向摆动,并为平面控制测量提供统一的起算基准,实现勘察设计、施工建设和运营维护各阶段控制网的“三网合一”,高速铁路采用GPS精密定位测量技术按一定间距(50~100 km)布设建立了框架控制网(CP0)。CP0控制点布设间距为50~100 km,与国际IGS参考站或国家CGCS2000 A、B级GPS点进行联测,采用GAMIT计算软件进行中长基线解算,解算精度要求较高[1]。
框架控制网(CP0)基线解算一般采用以时段为单位的多基线解算模式,数学模型严密,并能在结果中反映出同步观测基线之间的统计相关性[2],基线解算时首先需要选取联测的国际IGS参考站点或CGCS2000国家点作为已知起算点,然后根据IGS精密星历和载波相位观测值精确计算出基线向量及其方差协方差等精度信息,起算点的坐标精度将直接影响基线解算的精度乃至整个框架控制网的精度。在CP0基线解算过程中,为了使得起算点坐标偏差不至于影响到相对定位的精度,要求所给出的起算点坐标在其所在的地心地固坐标系中必须满足一定的绝对精度。选取工程测量数据进行处理分析,对高速铁路CP0基线解算中起算点坐标的允许精度进行研究,得出了一些有益的结论。
2 起算点误差对基线解算的影响分析
2.1 误差传播与影响模型
在CP0框架控制网基线解算过程中,需要将IGS参考站或CGCS2000国家点作为起算点,当起算点坐标出现误差或兼容性较差时将导致整个CP0框架控制网基线向量解产生系统性误差。试验表明,这种系统误差主要反映整网基线向量的系统性旋转和尺度的变化[7]。下面将从GPS相对定位原理的双差观测方程推导起算点对基线向量的误差传播与影响模型。
假设S1和S2是基线的两端点,在地心地固坐标系中的坐标分量分别为X1和X2,并以S1为起算点, ΔX12为S1、S2间的基线向量。若将S1作为起算点,并假设其坐标向量有微小变化δX1,则由此引起的S2的坐标变化可写作[3]
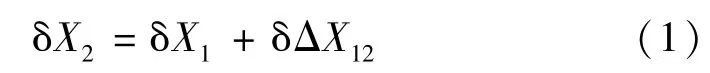
其中,δΔX12为起算点坐标的变化对所求基线的影响。
假设在测站i和测站j上对卫星p和卫星q进行同步观测后,在忽略大气折射残差影响的情况下,相对定位的双差观测方程为[2]
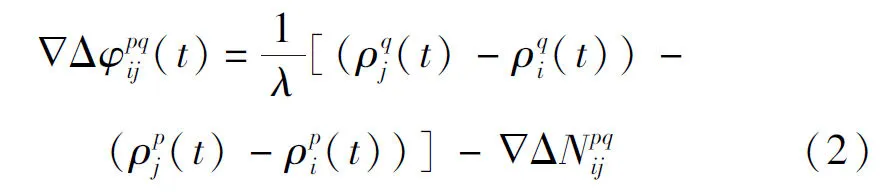

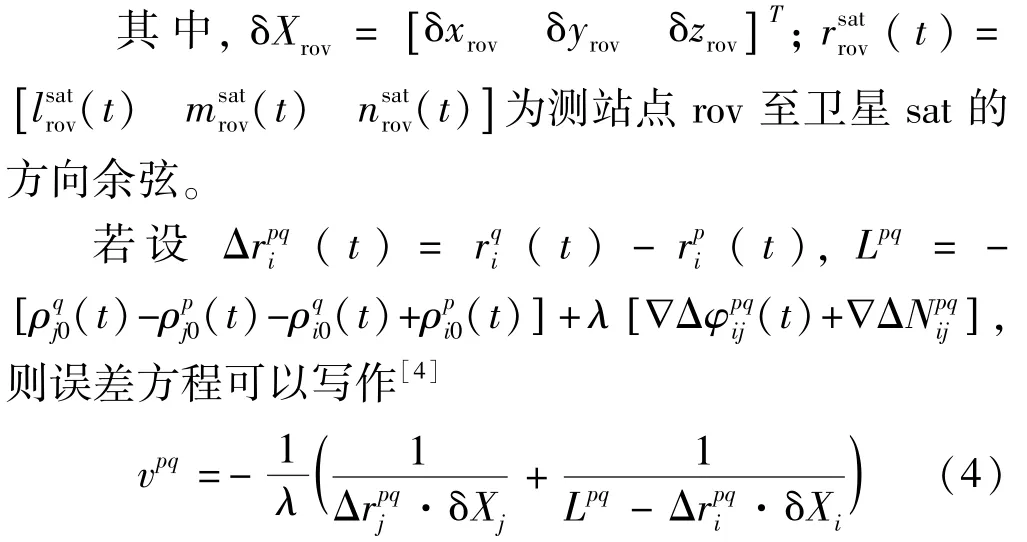
如果同步观测的卫星个数为n,并假设∇ΔN为已知,则误差方程可写成如下矩阵形式
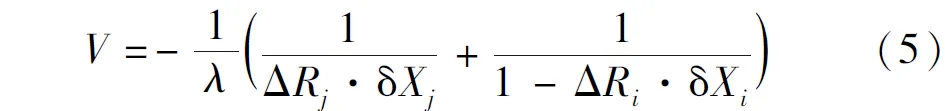
其中,V=[v12v13…v1n]T;ΔRrov= [ΔΔ…Δ]T,由公式(5)组成法方程,并整理得

式中,δR=ΔRj-ΔRi。
若设δXij为δXi的微小变化对基线向量的影响,根据公式(1)则有
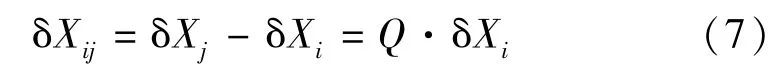
从上述公式可以看出,误差方程常数向量L和影响矩阵Q是与起算点初始坐标有关的量,将对误差方程的线性化精度和待定参数的改正数求解产生一定的影响;起算点坐标偏差对基线向量的影响与卫星间方向余弦有关,起算点坐标偏差的方向不同将导致基线向量误差的大小也不相同。
2.2 误差理论分析
大量的试验结果表明,起算点初始坐标误差对基线的最不利影响可用下式表示[5]

其中,δS为起算点初始坐标误差引起的基线误差,m;D为基线长度,km;δX1为起算坐标的误差,m。
计算出的初始坐标误差对基线最不利情况下的影响值见表1。

表1 初始坐标误差对基线的影响
由表1可知,GPS基线解算若以初始坐标误差对基线的影响量0.5 mm为限,基线处理时初始坐标误差应满足如下要求:对于短基线(小于10 km),其基准站初始坐标精度应优于1 m;对于中长基线(10~100 km),其基准站初始坐标精度应优于0.1 m;对于长基线(大于100 km),其基准站初始坐标精度应优于0.05 m。
3 起算点坐标精度对比研究
3.1 试验方案
选择国内某客运专线在勘测设计阶段建立的CP0框架控制网2013年6月9日(DOY160)和7月9日(DOY190)2 d的观测数据进行计算分析。控制网共布设6个控制点HJGT、TSGT、TUGT、WJGT、XDGT和ZJGT,点位布设间距为44~86 km,共联测6个IGS参考站点BJFS、WUHN、SHAO、URUM、DAEJ和TWTF。框架基准采用目前精度最高的ITRF2008参考框架,参考历元为2000.0。在GAMIT表文件sittbl.中对各控制点的测站三维坐标约束量进行设置,将IGS参考站作为起算点,约束量分别设置为0.03,0.03, 0.05 m;CP0控制点为待定点,采用长时间单点定位计算出的三维地心坐标作为其初始坐标,约束量分别设置为100,100,100 m。
为了比较起算点不同坐标精度对基线解算结果的影响,选用GAMIT 10.40基线解算软件分析数据,在参数设置均相同时,设计如下6种试验方案。
方案1:IGS起算点坐标不加误差;
方案2:IGS起算点坐标各方向加2 cm的误差, CP0待定点初始坐标不变;
方案3:IGS起算点坐标各方向加10 cm的误差, CP0待定点初始坐标不变;
方案4:IGS起算点坐标各方向加20 cm的误差, CP0待定点初始坐标不变;
方案5:IGS起算点坐标各方向加2 m的误差, CP0待定点初始坐标不变;
方案6:IGS起算点坐标各方向加20 m的误差, CP0待定点初始坐标不变。
GAMIT 10.40软件中基线解算其他相关参数设置见表2。
3.2 基线精度评定方法
(1)标准化均方根误差NRMS
GAMIT解算结果中的标准化均方根误差NRMS (Normalized Root Mean Square)可以用来衡量单时段解出的基线值偏离其加权平均值的程度,是从历元的模糊度解算中得出的残差,是衡量GAMIT解算结果的一个重要指标。根据国内外GPS数据处理经验,其值一般应小于0.3,若NRMS值太大,则说明处理过程中周跳可能未得到完全修复。其计算公式如下[6]

式中,Li和是基线向量(或边长)及其加权平均值,其对应方差为;n为同一观测时段基线数目。

表2 GAMIT参数设置
(2)基线分量改正量
一般来说,基线分量的改正量不能大于其站点坐标约束量的2倍。否则,需要查看Q文件或autcln. sum文件是否有大量观测数据被autcln模块运行时所删除。根据规范[8]要求,同时段观测值的数据剔除率宜小于10%。
(3)基线重复率
基线重复率是衡量GPS基线解算结果质量的重要指标之一,可以衡量多时段基线解的解算质量。其计算公式如下[6]
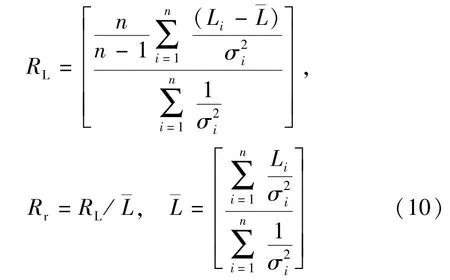
式中,RL为基线向量(或边长)的重复性;Rr为基线向量(或边长)的相对重复性;n为同一观测时段基线数目;Li为第i时段的基线分量(或边长);¯L为同一观测时段基线分量(或边长)的加权平均值。
进一步以单时段解的基线重复性为观测值,用线性拟合方法求出基线重复率的常数部分a以及与边长成比例的系数部分b

(4)基线分量较差
除了上述3个重要指标外,起算点坐标存在误差与无误差的各基线分量较差也是评判基线解算结果正确性的一个非常重要的参考指标。起算点存在误差与无误差时各基线分量较差越小,说明基线解算准确性和可靠性越高。
3.3 试验结果分析
(1)NRMS
图1是不同试验方案DOY160和DOY190两个单天解算结果的NRMS值。图中NRMS值均小于0.3,说明基线解算质量合格,但方案6中(即IGS起算点坐标误差为20 m时)各基线分量的均方差已达dm级,解算结果不可靠,存在错误。从图中可以看出,起算点坐标的误差大小在基线解算收敛的情况下对NRMS值的影响不大,且不同方案两个单天解的解算结果均没有表现出明显的规律,因此NRMS值的大小无法反映出起算点误差对基线解算精度的影响程度。
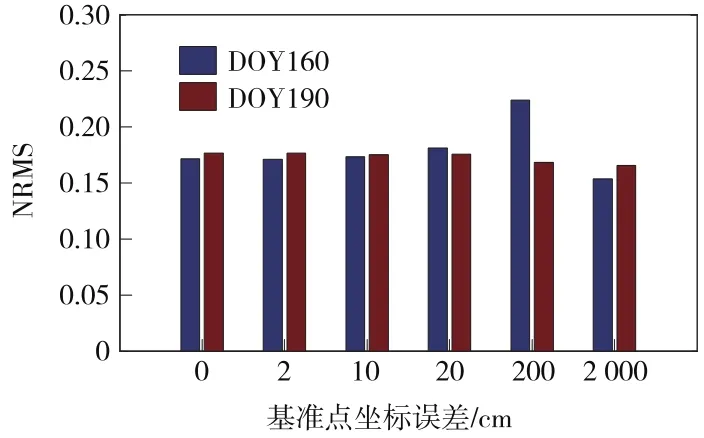
图1 不同方案解算结果的NRMS值
(2)基线分量改正量
图2是不同试验方案DOY160和DOY190两个单天解算结果的XYZ基线分量最大改正量。图中方案6中(即IGS起算点坐标误差为20 m时)DOY190单天解的基线分量最大改正量达0.345 m,大于其站点坐标约束量的2倍,说明基线解算结果不可靠,存在错误;其余各方案基线分量最大改正量为0.036 m,均小于其站点坐标约束量的2倍,说明基线解算质量合格。从图中可以看出,除方案6外,起算点坐标的误差大小在基线解算收敛的情况下对基线分量改正量的影响不大,不同方案两个单天解的解算结果没有表现出明显的规律性,因此也无法从基线分量改正量来判定何种方案更好。
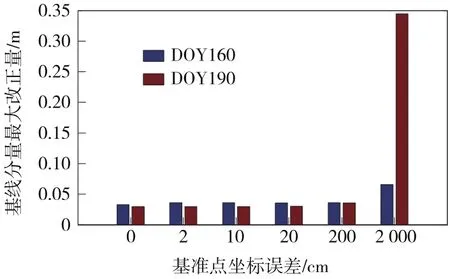
图2 不同方案基线分量最大改正量
(3)基线重复率
表3为不同试验方案解算结果三维地心坐标系下的基线向量和边长的重复率。基线重复率是根据基线解算结果采用公式(11)拟合得到的,由常数部分和系数部分组成,常数部分单位为mm,系数部分基线长度L的单位为m。

表3 不同方案解算结果的基线重复率
为了更直观地反映基线重复率误差的大小,对50 km长度基线的重复率所引起的绝对误差进行了计算,计算结果见图3。

图3 不同方案50 km长度基线重复率引起的绝对误差
从表3和图3可以看出,随着起算点坐标误差的增大,基线分量重复率随之增大,基线解算质量下降;当起算点坐标误差在2 cm以内时,基线解算精度较高,基本和无误差时相当;当起算点坐标误差达到10 cm时,基线重复率下降了一个量级,达到cm级,解算精度大幅度下降;当起算点坐标误差达到2 m时,基线重复率下降到dm级,解算结果可靠性大幅度下降;当起算点坐标误差达到20 m时,基线重复率已达dm级,解算结果不可靠,存在错误。因此可以看出, CP0框架控制网基线解算对于起算点坐标的精度要求是比较高的。
(4)基线分量较差
基线分量较差计算以CP0框架控制网中的6条基线为例,将方案1起算点无误差时的基线解算结果作为真值,分别得到方案2、3、4、5、6与方案1的各基线分量差值,各基线分量较差如图4所示。由于起算点坐标误差达到20 m时,基线解算结果不可靠,基线结果失去了参考价值,因此不再分析方案6与方案1的基线分量较差。
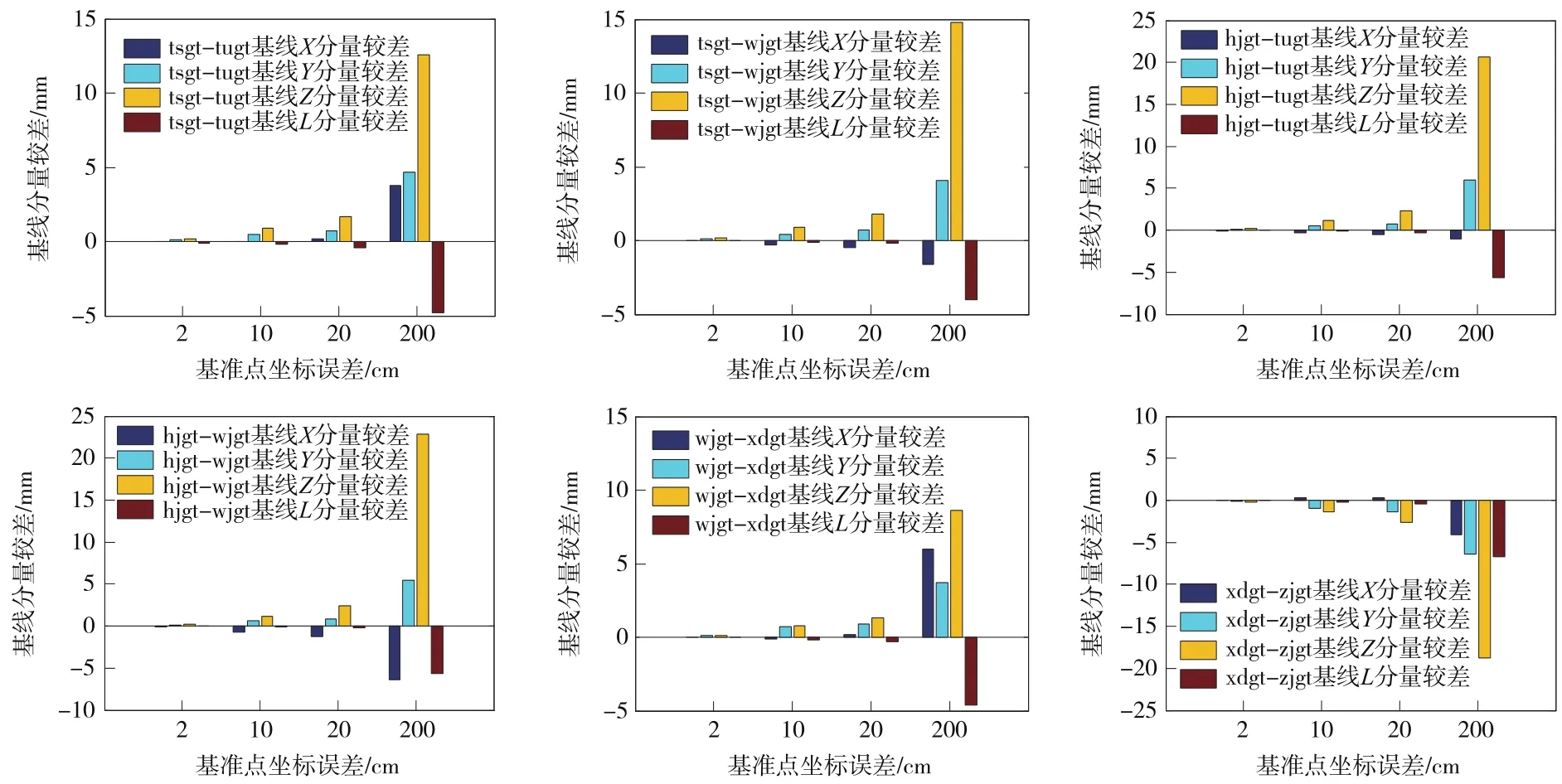
图4 不同方案基线分量较差
从图4可以看出,随着起算点坐标误差的增大,各基线分量较差(外符合精度)呈现出递减趋势,这和基线重复率(内符合精度)检验的结论一致;当起算点坐标误差在10 cm之内时,各基线分量的解算结果与方案1基本相同;当起算点坐标误差在20 cm之内时,各基线分量的解算结果与方案1差别在mm级的量级;当起算点坐标误差达到2 m时,各基线分量的解算结果与方案1的较差量级突增为cm级,最大达到2.28 cm,这表明基线解算结果已经不具有高精度,其可靠性大幅度降低;当起算点坐标误差达到20 m时,各基线分量的解算结果与方案1的较差突增至19.202 m,基线解算结果不可靠,已出现解算错误。
4 结论
本文选用实测工程测量数据对高速铁路CP0框架控制网数据处理过程中起算点坐标的允许精度进行了研究,得出如下结论。
(1)起算点坐标误差对CP0基线解算精度的影响是不容忽视的。起算点坐标偏差越大、基线长度越长,对基线解算结果的影响越大;另外,起算点坐标偏差对基线解算结果的影响呈现出一定的方向性。
(2)使用GAMIT软件进行CP0框架控制网解算时必须严格控制起算点坐标的误差,起算点点位坐标精度最好控制在10 cm之内;当起算点坐标误差达到20 cm时,各基线分量的解算结果的精度在mm级的量级;当起算点坐标误差达到2 m时,基线解算结果不可靠,不满足高精度解算要求。
(3)在CP0框架控制网基线解算过程中,需要将IGS参考站作为起算点,当起算点坐标出现误差或兼容性较差时,将导致整个CP0框架控制网基线向量解产生系统性旋转和尺度变化。为了确保起算点点位坐标精度满足基线解算的要求,IGS参考站测站坐标推荐使用IERS国际组织提供的基于某一参考框架参考历元的ITRF三维地心坐标(下载地址:http://itrf. ensg.ign.fr);对于多个国际组织(如IERS、IGS、SOPAC、JPL)均能提供坐标和速率的IGS参考站,应尽量收集2个或2个以上国际组织的数据对比分析,选择差异较小的参考站作为基准起算点,并优先采用最新的参考框架坐标和速率,在此基础上选用同一国际组织提供的地面基准站坐标和速率作为基线解算的强约束点;若需要其他框架和历元下的坐标,可以通过框架转换模型向前反推得到。
[1] 中华人民共和国铁道部.TB 10601—2009高速铁路工程测量规范[S].北京:中国铁道出版社,2009.
[2] 李征航,黄劲松.GPS测量与数据处理[M].2版.武汉:武汉大学出版社,2011.
[3] 刘基余,李征航,等.全球定位系统原理及其应用[M].北京:测绘出版社,1993.
[4] 戴中东,王瑞.起算点坐标偏差对静态GPS测量结果的影响[J].工程勘察,2008(5):67-69.
[5] 周忠谟,易杰军,周琪.GPS卫星测量原理与应用[M].北京:测绘出版社,1997.
[6] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.
[7] 姜卫平,刘经南,叶世榕.GPS形变监测网基线处理中系统误差的分析[J].武汉大学学报:信息科学版,2001,26(3):196-199.
[8] 国家质量技术监督局.GB/T18314—2001全球定位系统(GPS)测量规范[S].北京:中国标准出版社,2001.
[9] MIT.Department of Earth,Atmospheric,and Planetary Sciences. GPS Analysis at MIT(Release 10.4),2010.
[10]周东卫.GNSS参考站网络的对流层完备性监测技术研究[J].工程勘察,2012,40(10):65-70.
[11]余兴胜.构建桥涵勘测技术新体系的研究[J].铁道标准设计, 2013(2):73-76.
[12]田林亚,祖力比亚·阿布都热西提,等.高速铁路测量中高斯平面坐标与斜轴墨卡托平面坐标的转换[J].铁道标准设计,2013 (4):13-16.
Research on Accuracy of Initial Point Coordinate in Baseline Resolution for Frame Control Network of High-speed Railway
ZHOU Dong-wei
(China Railway the First Surveying and Design Institute Group Ltd.,Xi'an 710043,China)
In the process of high speed railway CP0 baseline resolution,it is necessary to set IGS reference stations as an initial point.Error or poor compatibility in terms of initial points will cause systemic rotation and scale change of baseline vector resolution for the entire frame control network. Therefore it is necessary to conduct a research on the essential accuracy of initial point for CP0 baseline resolution.In this paper,firstly,the error propagation and influence model of initial point coordinates is introduced and a theoretical analysis of the impact of initial point accuracy on baseline resolution is performed,and then surveying data in different resolution schemes are analyzed to determine the essential accuracy of initial points.The results show that,initial point errors must be strictly controlled while GAMIT software is used to resolve CP0 baselines,and initial point error is controlled as its best within 10 cm;when initial point error reaches 20 cm,each baseline component resolves in the millimeter level accuracy;when initial point error reaches 2 m,baseline resolution results are unreliable and can not meet the requirements of high precision calculating.
High speed railway;GPS;Initial point;Frame control network;IGS reference station;Accuracy
U238;P228
A
10.13238/j.issn.1004-2954.2014.12.010
1004-2954(2014)12-0040-05
2014-03-14
周东卫(1981—),男,高级工程师,2007年毕业于西南交通大学大地测量学与测量工程专业,工学硕士,E-mail:dwzhou810408@ 126.com。

