铁路客运站曲线站台加宽数学模型的探讨
朱长青
(中铁第四勘察设计院集团有限公司,武汉 430063)
铁路客运站曲线站台加宽数学模型的探讨
朱长青
(中铁第四勘察设计院集团有限公司,武汉 430063)
客运站的曲线站台需满足行车安全、旅客上下车安全以及圆滑美观的要求。从基本公式及相关规定出发,分析列车车体与站台边沿的动态距离,提出邻靠到发线和邻靠正线两种情况下的曲线站台边线的数学模型,并根据模型进行理论校验,结果证明建立的模型简洁可靠。
铁路客站;站台;曲线加宽;数学模型
1 概述
我国停靠动车的旅客站台,一般采用1.25 m高站台。受邻靠的铁路线路平面曲线的影响,站台边缘部分甚至全部需要做成曲线形。
曲线站台的使用主要有两种情况:一种是在客运站设计中,为缩短车站长度而将到发线曲线伸入站台内一定长度,曲线平面一般为圆曲线形;另一种情况是城际铁路的无配线车站,邻靠正线的站台有部分或者全部位于曲线内,曲线平面一般为缓和曲线形。
曲线站台设计需要满足两个方面的安全性:一方面为保证行车的限界安全,站台边缘与股道中心的间距需进行加宽;另一方面该加宽值要在一定的范围内,以保证车门与站台边缘足够密贴,不致使小孩的脚踏空发生危险。这两个方面是相互矛盾的,需要精确计算以采取合适的加宽值。近年曾发生因加宽考虑不足导致动车车体与站台边缘擦碰,或者因加宽过大而导致小孩掉入空隙的情况。
另外,高速客运站台面要求圆滑美观,不能做成折线形或者锯齿形,需要对站台边曲线建立一个简洁的数学模型以适应上述要求。
综上所述,对曲线站台加宽进行深入探讨具有较强的现实意义。
2 一般规定
2.1 基本加宽公式
《铁路技术管理规程》中规定加宽值按如下公式确定

式中 R——曲线半径,m;
H——计算点距轨顶高度,mm;
h——外轨超高,mm。
为保证站台与股道间距为一定值,站台边缘的曲线与相邻股道曲线应为同心圆。
2.2 规范中的加宽模型
(1)《高速铁路设计规范(试行)》中,曲线上建筑限界的加宽范围,包括全部圆曲线、缓和曲线和部分直线,采用图1所示阶梯加宽方法。

图1 客运专线建筑接近限界的曲线加宽方法(单位:m)
该方法中规定曲线上建筑限界的加宽范围,包括全部圆曲线、缓和曲线和部分直线,采用阶梯加宽方法,即缓和曲线中点前13 m至缓圆点之间加宽值规定为与圆曲线地段相同,缓和曲线中点前13 m至直缓点前22 m之间加宽值规定为圆曲线地段加宽值的二分之一。
(2)《站场及枢纽》中对加宽做了更加详细的规定,对无缓和曲线的曲线变加宽地段的加宽值计算方法为

式中 R——曲线半径,m;
x——计算点位置,直圆点为0点,m。该方法对内侧加宽采用了三次抛物线型,外侧加宽则采用了圆曲线线型。从公式中可以看出,该方法分段计算的衔接点加宽值不一致,在过渡段衔接部会产生错位而导致站台边为阶梯型。
一则部分地段冗余值过大,致使站台边缘与车门不密贴;二则不能满足个别控制点限界精确计算的要求,锯齿状的站台边缘不美观。因此该方法不适于客运站台,需要建立一个更为简洁的、圆滑的曲线数学模型来适应高速客运站台的需求。
3 邻靠到发线的站台过渡段曲线加宽
3.1 车体控制点动态分析
客车在线路上动态运行时,与相邻站台边缘的间距受车体最突出的部位控制。相对内侧站台,车体最突出的部位是车厢内侧的中部;而相对外侧站台,车体最突出的部位是车厢后端外侧,如图2所示。

图2 车体内、外侧加宽控制点示意
列车从直线向曲线方向运行,当前轮对通过ZY点时,车体内、外侧控制点即发生横向偏移。由于内、外侧控制点在纵向上与前转向架中心的距离不同,因此内、外侧加宽范围也不同。设车体长度26 m,转向架中心距18 m,当车体前轮对刚进入ZY点时,内侧控制点纵向距前转向架中心销为9 m,而外侧控制点为22 m(18 m+4 m)。因此,曲线内侧加宽范围为ZY点前方9 m,曲线外侧加宽范围为ZY点前方22 m。
为方便分析内、外侧控制点的运行轨迹,简化处理如图3所示。

图3 内、外侧控制点运行轨迹分析
如图3所示,列车从直线向曲线方向运行,前、后轮对依次通过ZY点的过程中,转向架前中心(C点)作轨道半径为R的圆周运动,后中心(O点)运行轨迹则为直线。
因为△OAB、△OEF与△OCD成相似三角形,因此该过程中的内侧控制点(A点)和外侧控制点(F点)也相应作圆周运动,且角速度相同、方向相反。
设C点的轨道半径为R,由于OC=2OA=4.5OF,则A点的轨道半径约为2R,F点的轨道半径约为4.5R。
3.2 过渡段数学模型的建立
根据3.1节的分析可知,内、外侧控制点运行轨迹为一段圆弧,因此内、外侧曲线加宽过渡段的数学模型应为圆方程。该弧线的起、终点即为车体前、后轮对先后通过ZY点时的状态值。
由于需要三点才能确定圆方程,中间的第三点可以采用插值法确定。当ZY点处于车体中心时,距离前、后轮对各9 m,此时分别计算出前、后控制点的偏移量,即可找出插值点的位置。
设内、外侧曲线同心圆全加宽分别为W内和W外。内侧加宽情况:过渡段曲线与同心圆曲线方向一致,轨迹半径为R/2,故控制点横向偏移量的中间值(B点)为W内/2。外侧加宽情况:过渡段曲线与同心圆曲线方向相反,轨迹半径为R/4.5。当车体运行处于图3的中间状态时,可知CD=81/2R,则EF=CD/ 4.5=9/R。
由于内侧加宽同时需要考虑曲线外轨超高的情况,因此内侧加宽适当放宽至20 m范围。数学模型如图4所示。
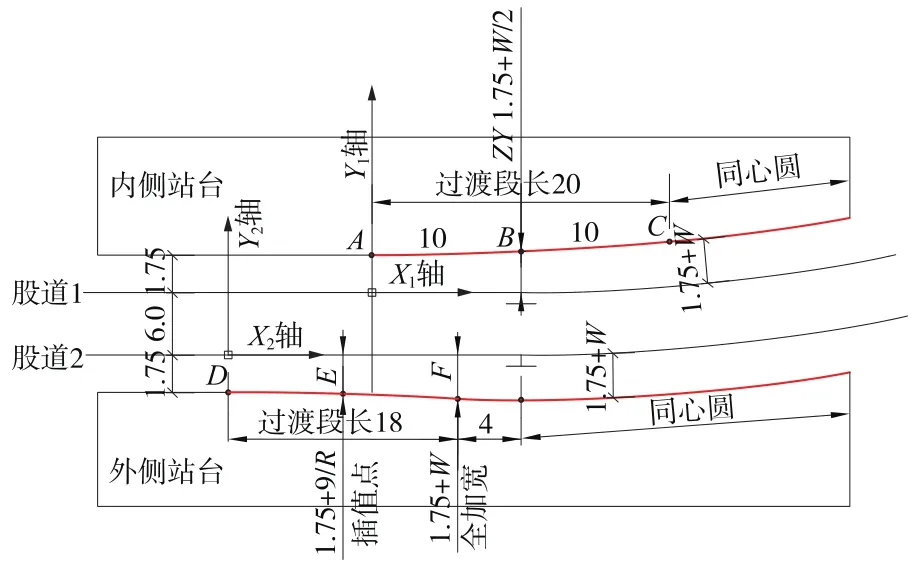
图4 内、外侧过渡段建模示意(单位:m)
3.3 内侧加宽过渡段数学方程求解
3.3.1 三点坐标计算
将过渡段长度适当延长并取整至ZY点前后各10 m,选取ZY点前10 m的零加宽点、ZY点处的半加宽点、ZY点后10 m的全加宽点,由此三点确定的圆弧作为过渡段曲线的线形,可以在autoCAD中使用三点定弧的作图法完成。
坐标系以股道中心为X轴,HZ点前10 m点为坐标原点,可以建立图4所示的X1—Y1轴直角坐标系。
设轨道曲线半径为R0,则内侧站台同心圆部分的边缘线数学方程为

取X=20,可以算出C点的坐标YC,从而可以进一步确定A、B、C三点坐标,分别为:A(0,1.75),B(10, 1.75+W内/2),C(20,YC)。
设过渡段曲线半径为r,圆心坐标为(x0,y0),则过渡段方程为

因此,求解半径及圆心坐标的值,过渡段的数学方程实际就确定了。
3.3.2 过渡段曲线半径计算
根据外接圆半径公式,有

其中,a=BC、b=AC、c=AB分别为三角形的三边长度。
为保证曲线半径r的计算精度至4位小数,a、b、c的值应精确到小数点后8位。
由于采用插值法进行的圆曲线模拟,该曲线半径近似于从∞至r的线性渐变,因此r≈2R0,R为过渡段范围站台边缘曲线半径,r则为全加宽范围站台边缘曲线半径。
3.3.3 过渡段圆心坐标计算
由于上述过渡段的模型是通过3点A(x1,y1),B (x2,y2),C(x3,y3)形成的圆,它的外接圆心O(x0,y0)的坐标为

例如,设R=1 200 m,W内=5 cm,代入上式可得Yc=1.841 731,过渡段曲线半径为2 396.386 2 m,圆心坐标为(-0.990 934,2 398.135 955)。
为精确求解曲线方程至毫米级(3位小数),上述各中间参数均应精确计算至8位小数。
3.4 外侧加宽过渡段数学方程求解
建立图4中所示的X2—Y2轴直角坐标系。设轨道曲线半径为R0,则外侧站台同心圆部分的边缘线数学方程为
(x-22)2+(y-R0)2=(R0+1.75+W外)2
取x=18,可以算出F点的y坐标YF,从而可以进一步确定D、E、F三点坐标,分别为:D(0,-1.75), E(9,-1.75-9/R0),F(20,YF)。
例如,设R0=600 m,则W外=44 000/600= 73.33 mm,YF=-1.810 0。
过渡段曲线半径、圆心坐标计算同样采用三点定圆的计算方法。计算过程同3.3节内侧加宽,篇幅有限不再详述。
3.5 过渡段数学模型的校验
无论何种数学模型,均可用图2中车体内、外侧加宽的控制点,在AutoCAD中使用作图法进行校验,以检核该数学模型在实际使用中的有效性。
为简化校验数据,本次选择了1 200、1 000、800 m和600 m四种典型曲线半径,在X取值5、10、15 m处分别对内、外侧控制点与站台边距离进行校验。(注: 20 m处为全加宽,无需校验。)
列车至站台边缘基本宽度1 750 mm,为车体半宽1 700 mm+安全保护间距50 mm构成。
表1中的折减后间距均在1 740 mm以上,由于动车组最大宽度为3 380 mm,即车体半宽为1 690 mm,在线路中心距站台边1 740 mm的实际距离下,车体控制点与站台边缘的实际距离仍保持在1 740-1 690= 50 mm。因此表1中的各项数据均满足安全保护间距的要求,上述过渡段数学模型校验是安全可行的。

_______________________________________表1 邻靠到发线的曲线站台加宽校验
4 邻靠正线的站台加宽
4.1 相关规定
受正线选线条件的限制,城际铁路的无配线站可能全部或者部分位于曲线上。
根据原铁道部《关于新建客运专线铁路曲线超高设定的指导意见》(铁集成[2009]86号)规定,进出站旅客列车超高值按以下要求设置(V为列车通过曲线时的速度)。
(1)当V≤160 km/h时,过超高一般不大于90 mm,困难条件下不大于110 mm;
(2)当160 km/h<V≤200 km/h时,过超高一般不大于70 mm,困难条件下不大于90 mm。
从表2可以看出,站台邻靠曲线时,正线需要限速。一般而言,曲线半径R≥2 000 m时,可以限速至160 km/h;1 600 m≤R<2 000 m时,可以限速至140 km/h;1 200 m≤R<1 600 m时,可以限速至120 km/h。

_____________表2 各种曲线半径限速值计算
《铁路技术管理规程》中规定邻靠正线的站台边缘,当行车速度V≤160 km/h时,直线部分的基本宽度采用1 780 mm。
4.2 数学模型的建立
根据铁路缓和曲线的定义,其曲率从∞至1/r线性渐变,外轨超高值也从0~h线性渐变。因此列车在经行缓和曲线的过程中,车体内、外侧各控制点的偏移加宽也是呈线性的。同理,曲线站台边缘的数学模型也只能选择缓和曲线的线型,并且在圆曲线部分与轨道中心的曲线保持同心圆,才能与渐变加宽的要求相适应。
根据铁路缓和曲线的方程定义,该曲线的曲率是从直线均匀过渡至圆曲线。因此,内、外侧站台与轨道之间的间距,也可以看成是从直线部分的基本宽度均匀过渡到圆曲线部分的加宽宽度。根据同心圆理论,可知:R内=R0-D0-W内,P内=P0+W内,

同理,可以求出外侧站台边缘的缓和曲线l外、R外,详见图5。

图5 内、外侧站台边线与轨道曲线关系示意

又由于正线运行速度较高致超高加宽较大,而曲线半径一般较大导致曲线加宽较小,因此总加宽值W外可能为负值,即轨道中心至站台边缘的距离可能小于直线地段的基本宽度。各种曲线半径下圆曲线范围内、外侧的全加宽计算值见表3。
根据图5中的公式计算出R内、P内或R外、P外,再根据l=计算出缓和曲线长度,则可根据半径和缓和曲线长建立缓和曲线方程:y=根据该数学方程可以计算出曲线上各点的平面坐标。

表3 各种曲线半径全加宽计算
表4中列出了轨道曲线半径在2 000、1 600 m和1 200 m三种情况下,对应的内、外侧站台边缘曲线要素(半径、偏移量、缓和曲线长)计算值。

表4 各种半径内、外侧站台边缘曲线要素计算
4.3 曲线加宽模型校验
参照本文3.3节中的校验模式,对靠正线缓和曲线模型的校验,选择半径/缓和曲线长2 000 m/210 m、1 600 m/200 m和1 200 m/180 m三种情况下,距ZH点 50、100、150 m和200 m典型位置的轨道中心至内、外侧站台边缘距离进行校核。校核方式为在AutoCAD中使用作图法进行校验,各点校验情况见表5。

表5 邻靠正线的曲线站台加宽校验
按照表5中模拟的3种曲线半径,在距离ZH点50、100、150、200 m各典型位置处的折减后间距均接近1 780 mm(基本间距),误差范围为±10 mm。
这个校验结果说明,在站台长度范围内车体经行的过程中,车体内、外侧控制点距离站台边缘的实际距离基本保持在1780 mm左右,因此上述模型是比较理想的。
5 结语
曲线站台对安全、美观的要求较高,因此需要对站台边缘的线型建立曲线方程以实现此功能。目前国内规范及论著中,主要采用分段计算渐变加宽的方法,该方法计算繁琐,常因顾此失彼导致计算错误,在设计及施工中操作困难。本文对邻靠到发线和邻靠正线两种情况,分别建立了简洁可靠的数学模型。经过CAD仿真校验,结果证明本文中建立的模型简捷可靠。
[1] 中华人民共和国铁道部.TB10621—2009高速铁路设计规范(试行)[S].北京:中国铁道出版社,2010.
[2] 中华人民共和国建设部.GB 50091—2006铁路车站及枢纽设计规范[S].北京:中国计划出版社,2006.
[3] 中华人民共和国建设部.GB 50090—2006铁路线路设计规范[S].北京:中国计划出版社,2006.
[4] 中华人民共和国铁道部.铁路工程设计技术手册站场与枢纽[M].中国铁道出版社,2004.
[5] 周兵和.铁路曲线限界加宽研究[J].铁道标准设计,2013(4).
[6] 侯江波,衣永亮.铁路缓和曲线的设计[J].科技传播,2012(10).
[7] 赵海燕.高速铁路缓和曲线设计研究[J].黑龙江科技信息, 2007(5).
[8] 李军.铁路高站台施工技术研究[D].南昌:南昌大学,2011.
[9] 欧阳全裕,王志培,姜传治.地铁曲线车站站台建筑限界计算研讨[J].城市轨道交通研究,2007(5).
[10]王锋,余惠林,赵晓华,路璐.关于地铁车站站台限界的探讨[J].铁道标准设计,2009(2).
[11]李映红.高速铁路信号系统[M].成都:西南交通大学出版社,2009.
[12]陈应先.高速铁路线路与车站设计[M].北京:中国铁道出版社,2001.
Approach to the Mathematical Model for Widening of Curve Platform in Passenger Station
ZHU Chang-qing
(China Railway Siyuan Survey and Design Institute Group Ltd.,Wuhan 430053,China)
Passenger station platform shall meet the requirements for traffic safety and the safety of passengers on and off the board.This paper analyzes the dynamic range between train body and platform edge based on the basic formula and related regulations,and presents mathematical models of curve platform edge line in two cases:the adjacent to hair line and adjacent to main line,and the theoretical verification is conducted based on the models.
Railway passenger station;Platform;Curve widening;Mathematical model
U291.6+5
A
10.13238/j.issn.1004-2954.2014.12.007
1004-2954(2014)12-0026-05
2014-03-31;
2014-04-22
朱长青(1974—),男,高级工程师,1997年毕业于北京交通大学铁路运输专业,工学学士,E-mail:758054313@qq.com。

