劈裂荷载下孔隙岩石应力分布特征与裂纹扩展行为

杨永明,鞠 杨,陈佳亮

(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京 100083; 3.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)

劈裂荷载下孔隙岩石应力分布特征与裂纹扩展行为

杨永明1,鞠 杨2,3,陈佳亮1

(1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京 100083; 3.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)

基于天然岩石孔隙结构重构模型,运用数值方法开展了不同孔隙率的圆盘劈裂数值模拟实验,研究了劈裂拉伸过程中孔隙岩石的裂纹扩展行为,从应力角度探讨了孔隙率对岩石裂纹扩展行为的影响;同时利用模型材料制作了不同孔隙率的孔隙岩石物理模型,开展了物理模型的劈裂实验,将实验结果和数值模拟结果进行比较,验证了数值模拟结果的有效性。经研究发现:在保持孔隙分布特征不变的条件下,孔隙率对圆盘劈裂破坏时的应力分布特征及裂纹扩展行为有显著的影响,随着孔隙率的增大,应力分布的对称性逐渐消失,最大拉应力值出现在远离对称轴孔隙密集的地方,且随着孔隙率的增加呈指数递减趋势。孔隙圆盘的破坏形式逐渐从单一劈拉破坏转变为劈拉和剪切破坏共存,导致最终破坏时形成多条开裂裂纹贯通圆盘。

岩石;孔隙结构;应力分布;裂纹扩展;数值分析

水力压裂(或水压致裂)是目前深埋低渗透高瓦斯煤层强化抽采的关键技术之一,煤与瓦斯共采中一个关键的基础科学问题是认知和探查在原岩应力场和水力压裂作用下岩石的裂纹扩展机理,然而由于深部岩体结构以及地质条件的复杂性,对岩体在原岩应力场作用下的破裂机理、压裂裂纹的空间扩展模式、展布特征和影响因素等认识不清,水力压裂技术应用尚处在经验的层面,缺乏科学性、系统性的理论指导。如能准确地描述和刻画原岩应力场作用下岩石的应力分布特征、裂纹扩展模式,对有效实施水压致裂、实现煤与瓦斯共采具有重要的理论意义。

岩石是一种复杂的不连续多孔介质,其内部存在着大量的孔隙,其数量众多、形态复杂且无序分布,荷载作用下岩石内部裂纹扩展行为极其复杂,导致目前关于孔隙岩石破坏时裂纹扩展行为的研究大都停留在连续介质力学的角度上,即将孔隙岩石看作一个连续介质而忽略内部的孔隙结构,利用数值模拟或实验的方法从宏观的角度分析岩石破坏时的裂纹扩展行为,如Wong L N Y和Einstein H H研究了单轴压缩条件下大理岩的裂纹扩展路径和开裂方式[1];Park C H和Bobet A利用模型实验分析了单轴压缩作用下岩石裂纹的开裂与闭合情况[2];E Sahouryeh等研究了双轴压缩作用下岩石断裂和裂纹扩展机理[3];陈卫忠等通过相似材料模型实验和数值计算方法研究裂纹起裂、扩展和贯通的机理[4];梁正召等从三维的角度出发,采用细观损伤数值模拟方法,模拟单轴压缩下含预制三维表面裂纹的岩石试样的破坏过程[5];柯建仲等利用离散元研究了各向异性岩石的裂纹扩展路径[6]。这些研究工作为人们认识荷载作用下岩石裂纹扩展机理创造了一定条件。

然而,目前岩石破坏裂纹扩展的分析基本属于“黑箱式”研究,人们无法获知裂纹扩展时岩石内部孔隙结构的变化及其对应力分布和裂纹扩展的影响,这种忽略内部孔隙结构、宏观式的研究方法难以准确和客观地阐述应力作用下一系列岩石裂纹扩展的内在机理,例如扩展裂纹长度、宽度和数量等几何特性与应力状态的关系;裂纹扩展方向与地层水平应力状态、孔隙结构、颗粒组成和岩性等之间的关系等,解决这些问题对于从理论上掌握岩石裂纹扩展机理具有十分重要的意义。

在一定的荷载条件下,岩石裂纹扩展规律与岩石内部应力分布状态密切相关,而孔隙结构严重影响着应力分布特征。因此如能准确地描述岩石内部孔隙结构,建立一个可靠的孔隙结构模型,利用这个模型,上述内部机理就可以确定出来。近年来,随着计算机和数值方法的发展,人们开始尝试通过各种数学或数值方法建立岩石孔隙模型[7－13],岩石孔隙模型的建立为解决孔隙岩石“黑箱式”的各种物理力学问题提供了一条有效的路径。

然而,天然孔隙岩石是一种复杂的多相介质,影响岩石裂纹扩展行为的因素众多,任何一种因素的变化都有可能导致裂纹扩展规律的改变,这给开展对比研究和识别岩石变形破坏时裂纹扩展形态造成很大的困难。因此,本文从单一影响因素——孔隙率入手来讨论孔隙结构对岩石劈裂拉伸破坏时应力分布特征和裂纹扩展行为的影响,利用CT扫描技术、统计学原理和自编程序构建了岩石孔隙结构三维模型,设计了不同孔隙率的三维模型,即模型固体相的物理力学性质以及孔隙的大小、形状和统计分布特征不变,但孔隙数量变化。运用数值实验方法,从应力角度入手分析了劈裂拉伸过程中孔隙率对岩石的裂纹扩展行为的影响。同时制作了与重构模型具有相同孔隙结构分布特征的孔隙岩石物理模型,开展了物理模型巴西圆盘劈裂物理实验,将实验结果和数值模拟进行了对比,验证了数值结果的有效性。先从单一影响因素——孔隙率入手,意在为进一步揭示孔隙岩石裂纹扩展微观机制提供基础,其他因素的影响在后续的研究中展开。

1 孔隙岩石的三维统计模型

基于天然岩石,利用CT扫描技术和统计学原理分析和研究了天然砂岩孔隙的几何特征与分布规律,给出了孔隙的形心坐标,孔隙间距、孔隙数和孔径的统计特征与各自分布的概率密度函数。分析结果表明,天然砂岩孔隙空间位置服从均匀分布,孔径满足指数分布,孔隙间距服从高斯分布[13]。同时借助FLAC3D程序和统计学原理构建了砂岩孔隙结构三维重构模型,重构模型与天然砂岩相比具有一致的孔隙分布特征和几何相似性。图1给出了应用上述重构方法生成的4种不同孔隙率的孔隙结构三维模型,孔隙率分别为3%,7%,15%和23%。需要说明的是,主要从细观角度分析孔隙对岩石应力分布和裂纹扩展的影响,因此,重构的三维孔隙模型是细观模型,尺寸较小,在视觉上看起来模型中的孔隙尺寸相比真实岩石中的孔隙要显得大些。同时,图1给出的是透视图,整个模型内部的孔隙都显示出来了,由于前后孔隙位置在同一视角上的重叠,所以在视觉上三维模型中的孔隙连成一片,尤其是高孔隙率模型。

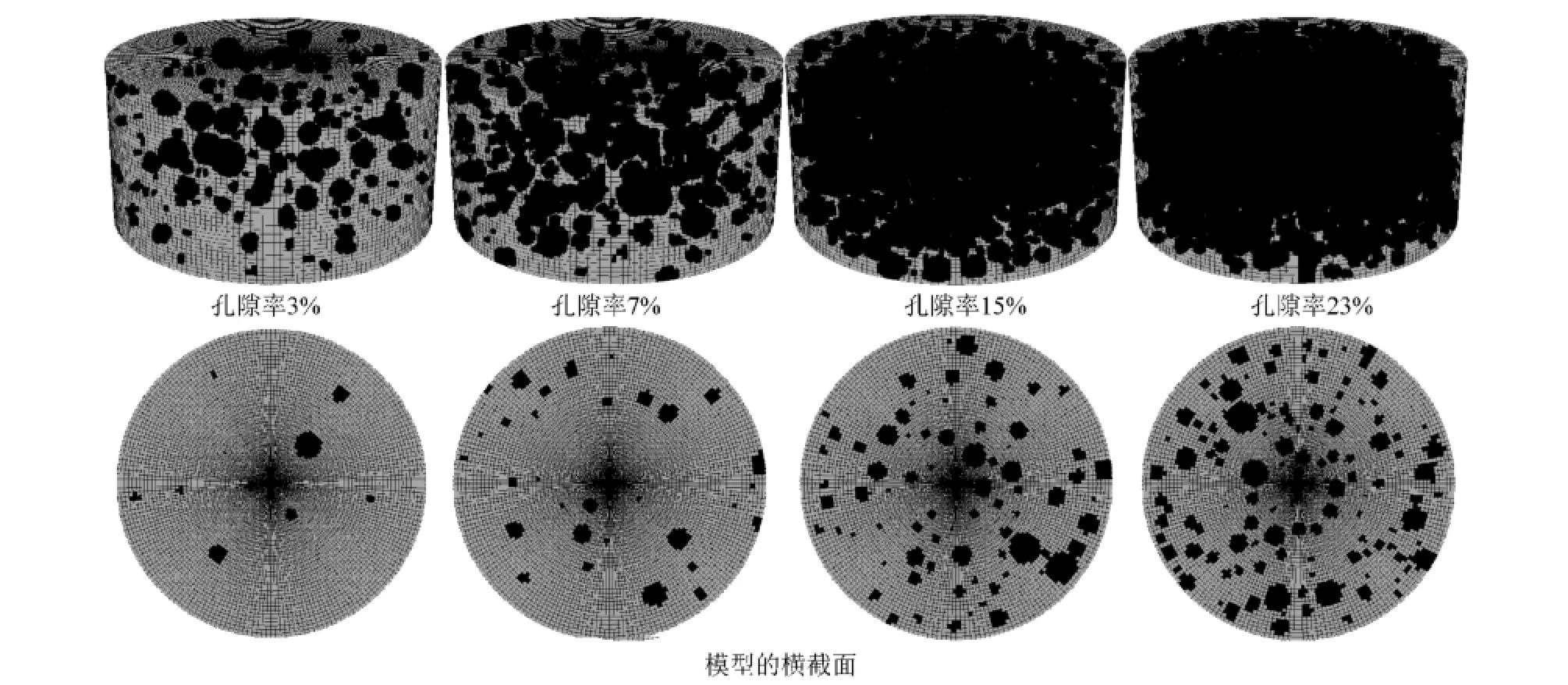
图1 孔隙岩石三维模型Fig.1 The 3D model of porous rock

2 孔隙岩石裂纹扩展行为的数值分析

为了对比和分析不同孔隙率对岩石裂纹扩展行为的影响,设计了5种不同孔隙率的孔隙模型(即保持孔径分布和孔隙空间位置分布特征函数不变,仅孔隙数量改变),从应力分布状态角度入手,分析了劈裂拉伸过程中孔隙率对岩石裂纹扩展规律的影响。除了上述4种孔隙率之外(3%,7%,15%和23%),还设计了一种无孔圆盘模型,计算了无孔圆盘模型劈裂时应力分布的理论解,对比分析了孔隙结构对岩石劈裂破坏过程中的应力分布特征及其裂纹扩展行为的影响规律。所有数值计算均采用FLAC3D软件完成,计算圆盘模型尺寸为25 mm×50 mm,选用天然砂岩的力学性能参数作为计算模型参数,具体如下:基质抗拉强度为1.17 MPa,剪切模量为7 GPa,体积模量为26.9 GPa,黏聚力为27.2 MPa,摩擦角为30°,破坏准则采用的是Mohr－Coulomb准则,在圆盘模型两端沿x方向施加等值的均布线荷载P,其余边界均为自由面。为在相同条件下分析和对比孔隙率对应力分布的影响,所有计算模型材料参数和边界条件是相同的。图2给出了加载和边界条件示意。

2.1 应力分布特征及对裂纹扩展的影响

为对比分析劈裂破坏过程中孔隙率对圆盘应力分布状态的影响,根据不同孔隙率圆盘破坏时的峰值荷载Pu(峰值荷载为进入塑性屈服的单元贯通整个模型时所施加的最大荷载),利用荷载比作为采样控制参数,分别提取了荷载达到峰值荷载Pu的5%, 30%,50%,70%和100%时的计算结果。图3给出了圆盘模型劈裂破坏过程中5个不同加载时刻的应力横截面。在劈裂实验中引起岩石劈裂破坏的主要应力因素是垂直于加载方向的应力,因此图中给出的是沿着y方向(圆盘横截面上加载方向为x方向)正应力σy的分布。图3中红色区域为拉应力;其余颜色的区域均为压应力。图4给出了劈裂裂纹扩展形态(图中利用不同颜色分别显示了由拉伸和剪切引起的塑性破坏区)。

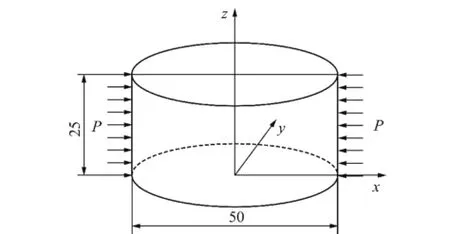
图2 加载边界条件示意Fig.2 Loading and boundary conditions

从应力计算结果可以直观地得出:

(1)对于无孔圆盘,即孔隙率为0时,在加载初期(即峰值荷载Pu的5%),除了加载两端附近出现小范围的拉应力区之外(图3中红色区域),圆盘整个横截面上的y方向正应力σy均为压应力。2个小范围拉应力区呈“锥形”沿圆盘y方向的直径左右对称分布;当荷载增加到峰值荷载的30%时,拉应力和压应力分布区域出现了明显的变化。拉应力区开始占据了圆盘横截面的中心大部分区域,并呈现“花苞”形状,且沿着圆盘x方向(即加载方向)的直径上下对称分布,而压应力仅出现在加载两端附近及圆盘的4个角上。拉应力和压应力的这种分布特征一直持续到峰值荷载的100%,即圆盘发生劈裂破坏。从上述分析结果可知,对于无孔圆盘,从峰值荷载的30%开始一直到峰值荷载,拉应力始终占据了圆盘中心的大部分区域,沿着圆盘x方向的直径具有很好的对称性。

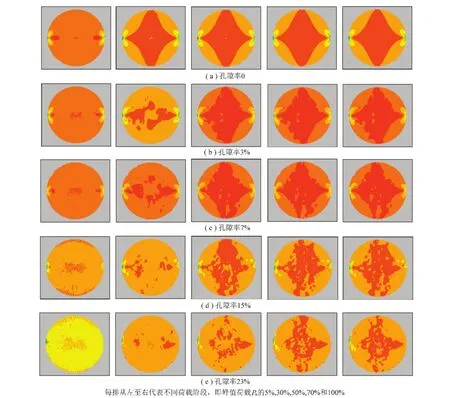
图3 劈裂破坏过程圆盘横截面沿y方向的正应力σyFig.3 The normal stress σydistribution along y direction in cross section of disk during splitting

图4 不同孔隙率模型劈裂裂纹扩展形态Fig.4 The fractured cracks of porous models with different porosities

(2)当孔隙率为3%和7%时,圆盘横截面的y方向正应力σy的分布特征和无孔圆盘相比有明显的差异。在加载初期(即峰值荷载Pu的5%),拉应力仍出现在加载两端附近的小范围区域,和无孔圆盘相比,由于孔隙的影响,分布区域形状的对称性减弱,同时在圆盘中心点也出现了微小的拉应力区,除此之外,其他区域都处于压应力状态。当荷载达到峰值荷载的30%时,和无孔圆盘相比,拉应力区没有占据圆盘横截面的大部分区域,而是主要集中在沿x方向的直径两边,而压应力仍占据了圆盘的大部分区域。当荷载达到峰值荷载的50%,拉应力区开始占据了圆盘横截面的大部分区域,由于孔隙的影响,沿x方向直径的对称性有所减弱,但仍有类似“花苞”形状的分布特性,压应力出现在加载两端附近及圆盘的四角上。当荷载继续增加直至破坏,拉应力和压应力的分布特性没有太大的变化,拉应力仍沿加载方向(x方向)近似对称的分布于圆盘中心的大部分区域,分布区域呈现类似“花苞”的形状,压应力仅出现在加载两端附近及圆盘的四角上。

(3)当孔隙率增加为15%和23%时,和低孔隙率圆盘相比,由于孔隙数量的增加,圆盘横截面的y方向正应力σy的分布特征有了明显的差异。在加载初期,加载两端附近没有出现拉应力,圆盘中心出现的拉应力区明显增大,同时在圆盘边缘处也出现了拉应力区,其他区域则为压应力区。当荷载达到峰值荷载的30%时,圆盘中心和四周边缘处的拉应力区消失,在低孔隙率圆盘中沿x方向的直径两边曾出现的拉应力区域的面积随着孔隙率的增加而减小,当孔隙率为23%时仅剩下2个很小的拉应力区出现在加载直径两边。当荷载增加到50%时,对于孔隙率15%的圆盘,拉应力开始占据了圆盘大部分区域,但在拉应力区的内部仍存在一些压应力区,即拉应力区和压应力区相互交错分布,拉应力区已经没有了对称性和“花苞”形状的分布特征;而对于孔隙率23%的圆盘,拉应力区分布则仍然很小,压应力仍占据着圆盘的大部分区域。直至达到峰值荷载,对于孔隙率23%的圆盘,拉应力将近占到了圆盘横截面面积的一半,相比其他孔隙率圆盘的拉应力区明显减小,拉应力区的分布完全没有了对称性和“花苞”形状,压应力区和拉应力区相互交错分布的现象更为明显。

由上述分析可知,孔隙对圆盘劈裂破坏时的应力分布特征有显著的影响,不同孔隙率圆盘的拉应力和压应力分布区域和形状有明显差异。无孔圆盘从加载开始一直到劈裂破坏,拉应力占据了圆盘中心的大部分区域,并呈现“花苞”分布形状,且沿圆盘x方向直径(与加载方向一致)对称分布,而压应力只出现在加载两端和圆盘四角的小范围区域。圆盘最终破坏是由拉应力引起的劈拉破坏,且一条劈裂主裂纹位于圆盘中间直径上,与x方向一致。对于孔隙圆盘,由于孔隙的存在改变了应力的分布特征,在峰值荷载时的拉应力区随着孔隙率的增加逐渐减小,压应力区则逐渐增大,拉应力区分布的对称性逐渐减弱,并开始呈现一种拉应力区和压应力区相互交错的分布形态,孔隙率越大,这种现象越明显。当孔隙率较低时,圆盘达到破坏时拉应力起主导作用,主要以劈拉破坏为主,但劈裂主裂纹开始偏离中间的对称轴,并出现了多条微裂纹。当孔隙率超过15%时,拉应力和压应力几乎占据同样大小的区域,圆盘最终破坏时出现了劈拉破坏和剪切破坏共同作用的破坏特征,没有了主裂纹,而是出现了多条劈裂裂纹。

2.2 最大拉应力分布特征及对裂纹扩展的影响

为进一步深入分析,提取了4种孔隙率圆盘达到峰值荷载时横截面上应力σy分布的数值解。同时根据弹性力学圆盘劈拉应力的理论公式(式(1)～(3))求解了无孔圆盘应力σy分布的理论解[14],将数值解和理论解进行比较,分析了孔隙率对应力分布大小的影响,进一步揭示孔隙率对岩石裂纹扩展行为的影响规律。

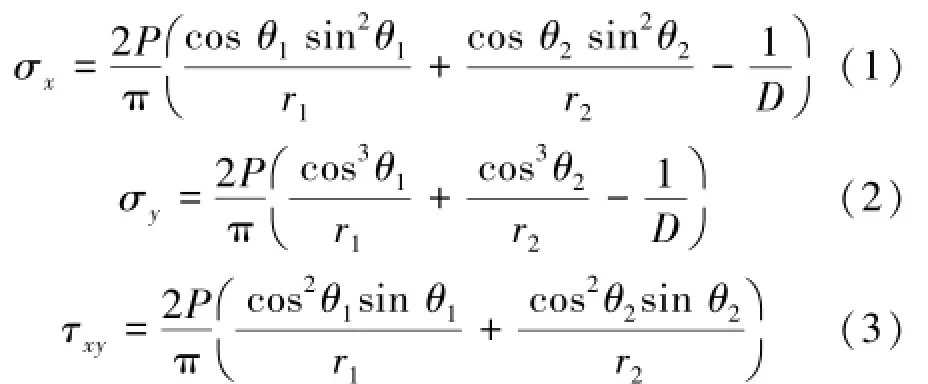
其中,压应力为正,拉应力为负;σx,σy,τxy分别为x, y两个方向的正应力和剪应力;P为施加的荷载;θ和r的几何含义如图5所示。图6给出了峰值荷载下圆盘横截面正应力σy的理论解和数值解的等值线云图。

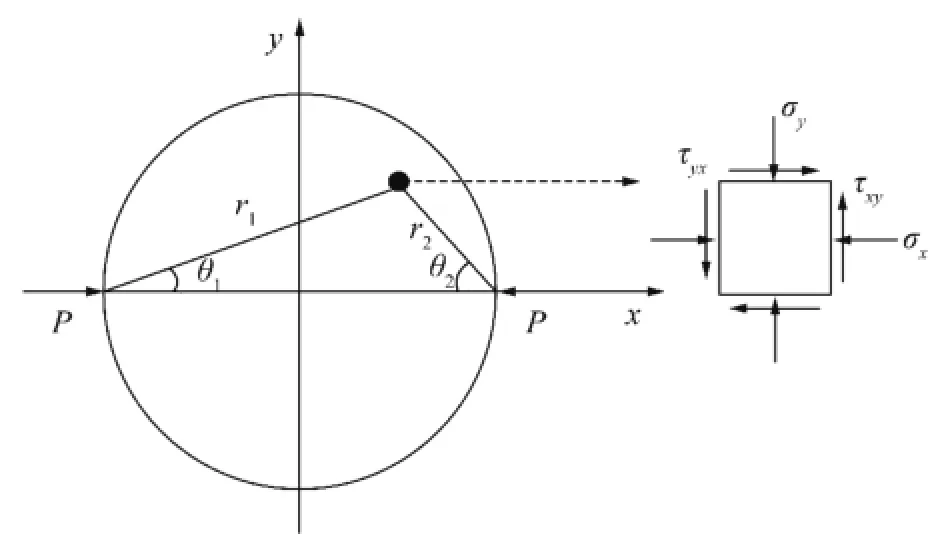
图5 圆盘应力理论解示意Fig.5 Stress theoretic solution of disc

经过分析可知:

根据弹性力学力的理论公式计算得到的无孔圆盘正应力σy在沿圆盘加载直径具有很好的对称性,在对称轴上出现了最大拉应力值,且沿着对称轴方向大小不变(除加载两端附近),其值为1.17 MPa,和选取的计算材料的抗拉强度值相等,在中间对称轴上的最大拉应力值即为材料的抗拉强度值。对于孔隙圆盘,孔隙严重地影响了孔隙圆盘正应力σy的分布特征。随着孔隙率的增大,沿加载直径的对称性开始减弱,孔隙率增加到15%以上,已没有了对称性可言,最大拉应力值出现的区域随着应力分布对称性的消失,逐渐偏离了对称轴,出现在孔隙密集的地方,当孔隙率为3%时,最大拉应力值为1.059 MPa;孔隙率为7%时,最大拉应力值为0.935 9 MPa;孔隙率为15%时,最大拉应力值为0.706 9 MPa;孔隙率为23%时,最大拉应力值为0.551 7 MPa。相比无孔圆盘的最大拉应力值,随着孔隙率的增大,最大拉应力值减小的百分比分别为9.49%,19.7%,39.58%和52.85%,数值进行拟合可以得知,随孔隙率的增加,最大拉应力值呈现指数递减趋势,图7给出了拟合曲线,拟合公式的具体表达式为

式中,ρ为孔隙率;a,b和c为待定参数,根据本文计算所得的结果,建议参考值a=1.15,b=29.74和c= 0.016。

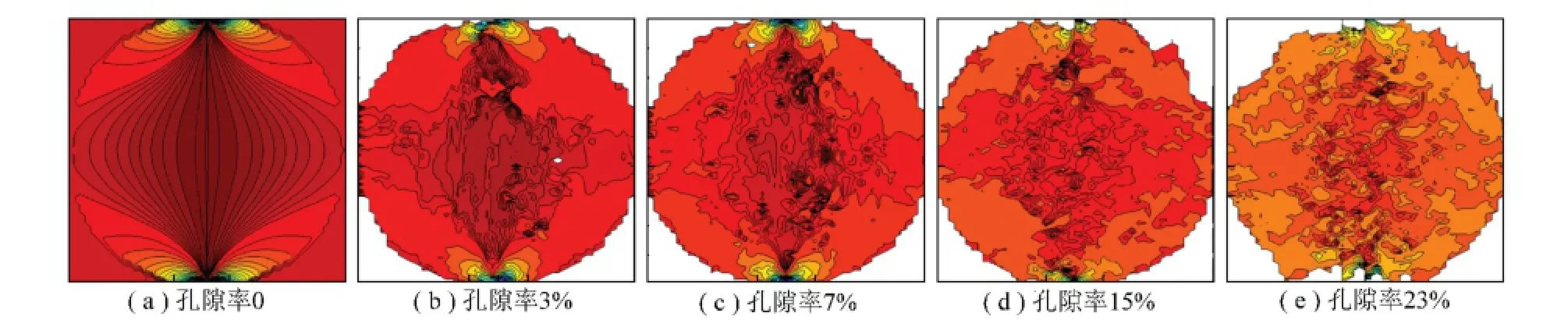
图6 不同孔隙率圆盘的正应力σy分布等值线Fig.6 The normal stress σydistribution isogram of disks with different porosities

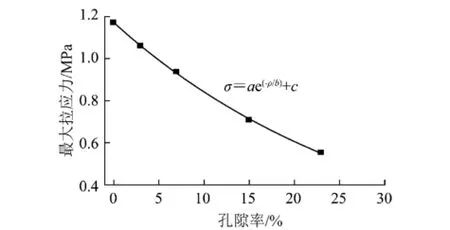
图7 最大拉应力值随孔隙率变化的曲线Fig.7 The distribution curve of maximum tensile stress with different porosities

综上,由于孔隙的存在,改变了圆盘最大拉应力的大小和分布区域,导致孔隙圆盘的破坏随着孔隙率的增加形式从单一劈拉破坏转变为劈拉和剪切破坏共存,破坏裂纹由一条主裂纹变成了多条裂纹。验证了前述通过应力分布状态得到的结论。

3 孔隙物理模型的劈裂实验

为了突出孔隙率这一影响因素,消除其他因素对孔隙岩石应力分布特征和裂纹扩展行为的影响,同时为验证上述基于三维孔隙模型数值计算结果的有效性,利用模型材料制作了孔隙岩石物理模型,采用水泥砂浆和聚苯乙烯颗粒分别来模拟岩石的固相介质和孔隙部分。水泥砂浆具有取料方便,易加工,材料力学性能和岩石相似等特性;聚苯乙烯颗粒具有一定的形状,质量轻、强度低、内有空气层,与实际孔隙相的物理力学性质相近。为保证物理模型的孔隙分布特征与真实岩石的孔隙结构分布特征保持一致,利用CT扫描检测了物理模型孔隙的统计特征及分布规律,结果表明孔隙物理模型的孔隙结构与天然砂岩相比具有较好的一致性[15]。所有孔隙模型都是经过同样的配比、加工方式和养护方法制作而成,因此可以认为所有制作的圆盘试件的物理力学性质一致(水泥砂浆的材料配比详见表1)。

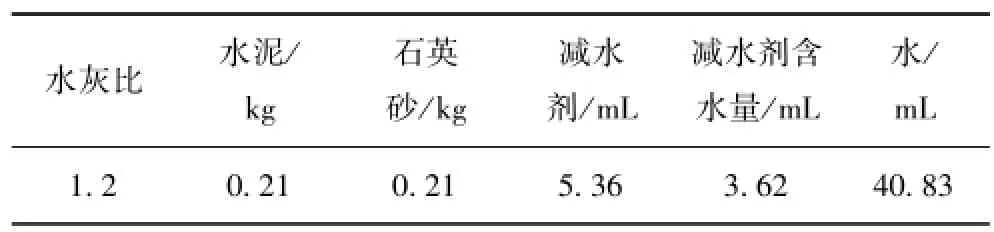
表1 水泥砂浆材料配比Table 1 The proportion of concrete

共加工了4种孔隙率的物理圆盘模型,为了消除实验结果的离散性,每种孔隙率物理模型制备了3个,共12个物理模型样品,尺寸均为50 mm×25 mm。每个模型样品里的聚苯乙烯颗粒数量和尺寸级配严格按照天然砂岩孔隙尺寸的统计分布函数和孔隙率来确定的[15]。

基于4种孔隙率的物理模型,开展了一系列巴西劈裂CT实时扫描实验。图8给出了不同孔隙率物理圆盘模型劈裂破坏时的裂纹扩展形态CT扫描横截面图(因篇幅所限,每种孔隙率选取了其中一个试件中间一层横截面层作为代表层),图中沿着裂纹的扩展方向即为劈裂荷载的加载方向。

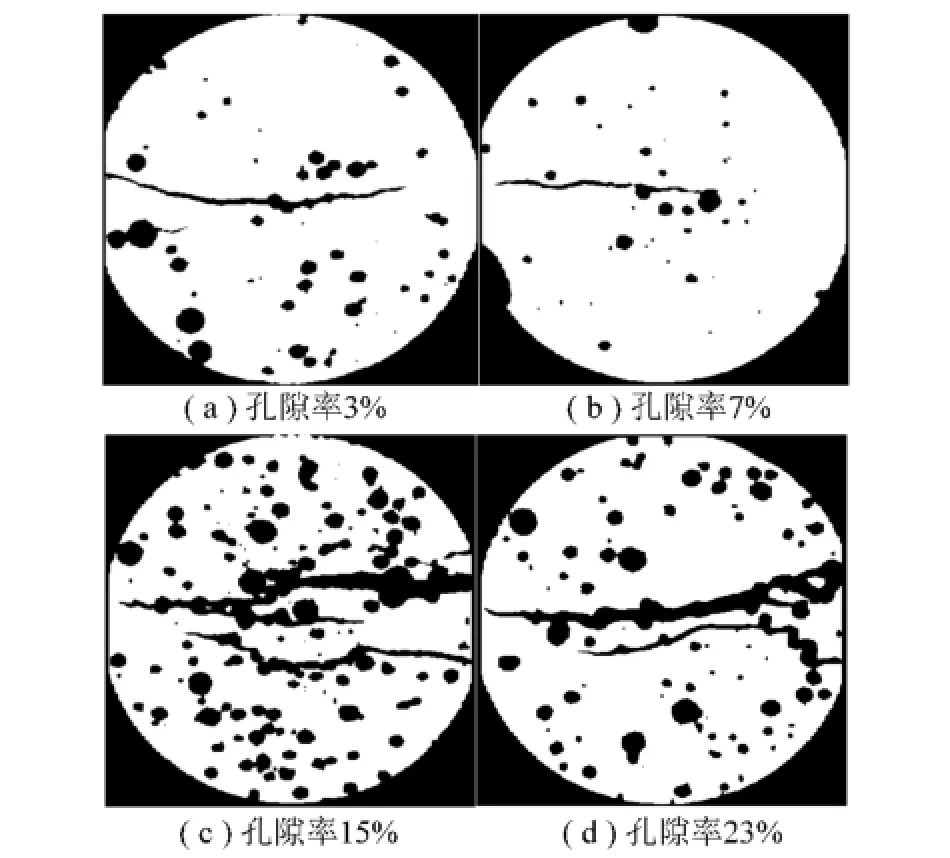
图8 不同孔隙率圆盘裂纹扩展形态CT扫描图Fig.8 The CT scanning images of cracks growth morphology with different porosities

从CT扫描图中可以看出,孔隙显著影响着劈裂裂纹的扩展形态。孔隙率较低时(3%和7%),圆盘破坏时只出现了一条开裂裂纹,位于圆盘中间纵向直径附近,近似为一条直线,由此可知,小孔隙率物理模型主要以拉伸破坏为主;当孔隙率增大时(15%和23%),除了一条主裂纹外,在孔隙密集的地方还出现了多条次裂纹,孔隙率越大,裂纹数越多,主裂纹严重偏离了对称轴,因此大孔隙率物理模型破坏时存在拉伸和剪切破坏共同作用。上述裂纹扩展形态可以印证前述基于孔隙三维模型数值模拟分析得到的应力分布特征:有孔圆盘应力分布对称性随着孔隙率的增大而逐渐减弱,最大拉应力值逐渐偏离对称轴,导致裂纹位置偏离了对称轴。和无孔时相比,拉应力区有所减小,但孔隙率较低时拉应力仍对破坏起主导作用,最终以劈拉破坏为主,导致只出现一条主裂纹。随着孔隙率的增大,拉应力区和压应力区相互交错分布,对破坏起到同样的作用,导致最终破坏时形成多条劈裂裂纹,同时劈裂裂纹严重偏离了对称轴。

4 结 论

(1)在保持孔隙分布特征不变的条件下,孔隙对圆盘劈裂破坏时的应力分布特征有显著的影响,不同孔隙率圆盘的拉应力和压应力分布区域和形状有明显差异。无孔圆盘应力分布呈现“花苞”形状,且沿圆盘加载直径对称分布,圆盘最终破坏是由拉应力引起的劈拉破坏,且一条主裂纹位于圆盘中间加载方向的直径上。随着孔隙率的增大,应力分布的对称性逐渐减弱,开始呈现一种拉应力区和压应力区相互交错的分布形态,孔隙率越大,交错现象越明显。当孔隙率较低时,圆盘主要以劈拉破坏为主,当孔隙率超过15%时,圆盘最终破坏时出现了劈拉破坏和剪切破坏共同作用的破坏特征,劈裂裂纹严重偏离了中间对称轴,出现了多条劈裂裂纹。

(2)无孔圆盘对称轴上出现了最大拉应力值,且沿着对称轴不变(除加载两端附近),峰值荷载条件下最大拉应力值为材料的抗拉强度值。对于孔隙圆盘,应力沿加载直径的对称性随着孔隙率的增大而逐渐减弱,最大拉应力值出现的区域随着应力分布对称性的消失,逐渐偏离了对称轴,出现在孔隙密集的地方,最大拉应力值随着孔隙率的增加呈指数递减趋势,孔隙圆盘的破坏形式逐渐从单一劈拉破坏转变为劈拉和剪切破坏共存,峰值荷载条件下的最大拉应力值已不能作为材料的抗拉强度值。

(3)孔隙岩石物理模型的巴西劈裂CT实时扫描实验表明:孔隙圆盘应力分布对称性随着孔隙率的增大而逐渐减弱,最大拉应力值逐渐偏离对称轴,导致裂纹位置偏离了对称轴。和无孔时相比,拉应力区有所减小,但孔隙率较低时拉应力仍对破坏起主导作用,最终以劈拉破坏为主,导致只出现一条开裂裂纹。随着孔隙率的增大,拉应力区和压应力区相互交错分布,对破坏起到同样的作用,导致最终破坏时形成多条开裂裂纹,严重偏离了对称轴。

[1] Wong L N Y,Einstein H H.Systematic evaluation of cracking behaviour in specimens containing single flaws under uniaxial compression [J].International Journal of Rock Mechanics and Mining Sciences, 2009,46(2):239－249.

[2] Park C H,Bobet A.Crack coalescence in specimens with open and closed flaws:A comparison[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(2):819－829.

[3] Sahouryeh E,Dyskin A V,Germanovich L N.Crack growth under biaxial compression[J].Engineering Fracture Mechanics,2002,69 (18):2187－2198.

[4] 陈卫忠,李术才,朱维申,等.岩石裂纹扩展的实验与数值分析研究[J].岩石力学与工程学报,2003,22(1):18－23.

Chen Weizhong,Li Shucai,Zhu Weishen,et al.Experimental and numerical research on crack propagation in rock under compression [J].Chinese Journal of Rock Mechanics and Engineering,2003,22 (1):18－23.

[5] 梁正召,李连崇,唐世斌,等.岩石三维表面裂纹扩展机理数值模拟研究[J].岩土工程学报,2011,33(10):1615－1622.

Liang Zhengzhao,Li Lianchong,Tang Shibin,et al.3D numerical simulation of growth of surface crack of rock specimens[J].Chinese Journal of Geotechnical Engineering,2011,33(10):1615－1622.

[6] 柯建仲,许世孟,陈昭旭,等.基于边界元法各向异性岩石的裂纹传播路径分析[J].岩石力学与工程学报,2010,29(1):34－42.

Ke Jianzhong,Xu Shimeng,Chen Zhaoxu,et al.Boundary elementanalysis of crack propagation paths in anisotropic rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):34－42.

[7] Barla G.The distribution of stress around a single underground opening in a layered medium under gravity loading[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1972,9(1):127－154.

[8] Lock P A,Jing X D,Zimmerman R W,et al.Predicting the permeability of sandstone from image analysis of pore structure[J].Journal of Applied Physics,2002,92(10):6311－6319.

[9] Okabe H,Blunt M J.Prediction of permeability for porous media reconstructed using multiple-point statistics[J].Physical Review E, 2004,70(6):66135－66145.

[10] 刘堂晏,肖立志,傅容删,等.球管孔隙模型的核磁共振(NMR)弛豫特征及应用[J].地球物理学报,2004,47(4):663－671.

Liu Tangyan,Xiao Lizhi,Fu Rongshan,et al.Applications and characterization of NMR relation derived from sphere-capillary model[J].Chinese Journal of Geophysics,2004,47(4):663－671.

[11] Bryant S,Blunt M.Prediction of relative permeab-ility in simple porous media[J].Phys.Rev.A,1992,46:2004－2011.

[12] 王宝善,陈 颙,葛洪魁,等.高孔隙岩石变形的离散单元模型[J].地球物理学报,2005,48(6):1336－1342.

Wang Baoshan,Chen Yu,Ge Hongkui,et al.A discrete element model of porous rock deformation[J].Chinese Journal of Geophysics,2005,48(6):1336－1342.

[13] Ju Yang,Yang Yongming,Song Zhenduo,et al.A statistical model for porous structure of rocks[J].Science in China Series E:Technological Sciences,2008,51(11):2040－2058.

[14] Мусхелишьили H И.数学弹性力学的几个基本问题[M].赵惠元译.北京:科学出版社,1958:249－251.

[15] 杨永明,鞠 杨,王会杰.孔隙岩石的物理模型与破坏力学行为分析[J].岩土工程学报,2010,32(5):736－744.

Yang Yongming,Ju Yang,Wang Huijie.Physical model and failure analysis of porous rock[J].Chinese Journal of Geotechnical Engineering,2010,32(5):736－744.

Distribution properties of stress and cracks propagation behavior of porous rocks during splitting

YANG Yong-ming1,JU Yang2,3,CHEN Jia-liang1

(1.School of Mechanics&Civil Engineering,China University of Mining and Technology(Beijing),Beijing 100083,China;2.State Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology(Beijing),Beijing 100083,China;3.State Key Laboratory for Geomechanics&Deep underground Engineering,China University of Mining and Technology,Xuzhou 221008,China)

Based on the 3D reconstruction models of natural porous rock,the Brazil disk splitting tests were simulated using numerical method.The fracture behavior of porous rock was investigated during splitting.The influence of porosity on cracks growth was probed in porous rock from the view of stress.In the meantime,the physical models of porous rock were fabricated using similar material.Based on the physical models with varied porosities,the Brazil disk physical tests were carried out.The experimental results verified the validity of numerical results.It is shown that the porosity seriously affects the stress distribution features and cracks growth of rock during splitting when the distribution characters of pores being changeless.With the increase of porosity,the symmetry of stress distribution gradually disappears.The maximum tensile stress deviates from the symmetry axis and lies on the region with intensive pores.With the increase of porosity,the maximum value decreases gradually in exponential function.The failure mode changes from single tensile failure to tensile failure and shear failure.It leads to multiple cracks run through the disk.

rock;porous structure;stress distribution;crack propagation;numerical analysis

TD315

A

0253－9993(2014)04－0658－08

杨永明,鞠 杨,陈佳亮.劈裂荷载下孔隙岩石应力分布特征与裂纹扩展行为[J].煤炭学报,2014,39(4):658－665.

10.13225/j.cnki.jccs.2013.0513

Yang Yongming,Ju Yang,Chen Jialiang.Distribution properties of stress and cracks propagation behavior of porous rocks during splitting [J].Journal of China Coal Society,2014,39(4):658－665.doi:10.13225/j.cnki.jccs.2013.0513

2013－04－19 责任编辑:常 琛

国家杰出青年科学基金资助项目(51125017);国家自然科学基金资助项目(51374213);煤炭资源与安全开采国家重点实验室开放课题资助项目(SKLCRSM13KFB09)

杨永明(1979—),男,山西岚县人,讲师,博士后。Tel:010－62331253,E－mail:yym113@163.com