基于2D-PCA的两级LDA人脸识别方法

王友钊,潘芬兰,黄 静

(1.浙江大学数字技术及仪器研究所,杭州310027;2.浙江理工大学信息学院,杭州310018)

基于2D-PCA的两级LDA人脸识别方法

王友钊1,潘芬兰1,黄 静2

(1.浙江大学数字技术及仪器研究所,杭州310027;2.浙江理工大学信息学院,杭州310018)

线性鉴别分析(LDA)小样本问题的已有解决方法在构造最优投影子空间时未完整利用LDA的4个信息空间,为此,提出一种基于二维主成分分析(2D-PCA)的两级LDA人脸识别方法。采用减法运算对样本类内散度矩阵和类间散度矩阵的特征值矩阵求逆,以解决小样本问题,并连续应用Fisher准则和修改后的Fisher准则连接2个投影子空间,获取包含LDA的4个信息空间的最优投影方向,利用2D-PCA对输入样本做预处理,以减少计算复杂度。在ORL和YALE人脸库上的实验结果表明,该方法虽然训练时间略有增加,但识别率分别为92.5%和95.8%,优于其他常用LDA算法。

线性鉴别分析;直接线性鉴别分析;二维主成分分析;小样本问题;人脸识别;特征提取

1 概述

线性鉴别分析(Linear Discriminant Analysis, LDA)是一种重要的特征提取方法,在人脸识别领域得到了广泛的应用[1-2]。它基于Fisher准则,目的是寻找一组将高维样本投影到低维空间的最佳投影向量,使所有投影样本的类内散度最小且类间散度最大。然而,在人脸图像识别领域,训练样本的数量通常小于每一个样本的维数,且样本的类内散度矩阵奇异,难以直接应用Fisher准则。

针对小样本问题,文献[3]利用主成分分析(Principal Component Analysis,PCA)将高维空间的样本投影到低维空间以保证样本类内散度矩阵非奇异,然而该方法的问题在于利用PCA降维的同时也丢失了较多的鉴别信息。文献[4]提出的直接LDA(Direct LDA,DLDA)方法虽不需要通过PCA降维来解决小样本问题,却丢弃了类间散度矩阵的零空间,且其对类间散度矩阵特征值的求逆导致没有充分利用它的列空间信息[5]。对称零空间LDA方法通过构造类内和类间散度矩阵的2个零子空间及其互补子空间,改善了人脸特征的鉴别力[6],基于集成学习的规范化LDA方法通过迭代过程提高了信息的可分离性[7]。正则LDA(Regularized LDA,RLDA)方法通过给类内散度矩阵的特征值加上一个正则参数[8]或通过指数拟合[9]使类内散度矩阵非奇异,再使用Fisher准则求解。RLDA虽然克服了DLDA的不足,充分利用了类内散度矩阵的零空间和类间散度矩阵的列空间,却由于类内散度矩阵的求逆使它的列空间信息没有充分利用。而在LDA算法的4个信息空间中,虽然类间散度矩阵的零空间和类内散度矩阵的列空间信息的鉴别力不如其他2个,却依然包含着对分类有用的信息[10-11]。

2 二维主成分分析

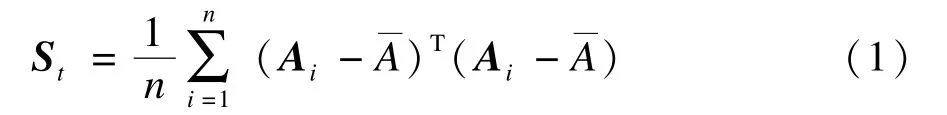
极大化式(2)且满足标准正交条件的一组向量,也就是St的较大特征值所对应的特征向量X1,X2,…, Xd,即2D-PCA[12]的最优投影方向Wopt。则对任一已知的图像样本Ai,它在最优投影方向Wopt上的特征矩阵为:

3 两级线性判别分析方法

3.1 传统Fisher准则的应用

经过2D-PCA降维处理,m×l维的图像Ai变成m×d维矩阵A′i,将A′i转换成r维列向量ai,其中, r=m×d,则训练集U={A1,A2,…,An}变为U′= {a1,a2,…,an}。由于模式类别为c,U′也可被分为c个子集U′1,U′2,…,U′c。

令μj为U′i的样本均值,μ为U′的样本均值,则U′的类间散度矩阵SB为:

U′的类内散度矩阵SW为c个子集的散度矩阵的和:

传统LDA方法寻找线性变换G∈Rk×r,使变换后的k维空间的类间散度与类内散度之比最大,即解答下面传统Fisher准则的最优问题:

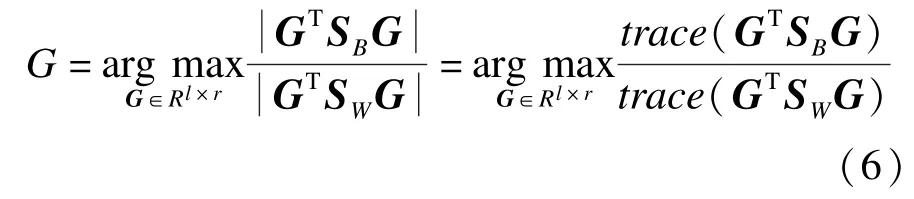
在小样本情况下,r＞n,因此,散度矩阵SB,SW奇异,且它们的秩分别为rb=c-1,rw=n-c。分别对SB和SW做特征值分解可得:

对SW特征值的平方根矩阵DW求逆后,小的特征值将变大,而大的特征值会变小,因此,本文算法通过对DW进行减法运算以估计DW的逆矩阵:

其中,λ为任意正数;α是SW的最大特征值;I是与SW相同维数的单位矩阵。由于SW为半正定矩阵,因此它的特征值大于等于0。如果λ＜1,则Dα中至少会有一个值小于0,违反了SW是半正定矩阵的性质,因此,λ≥1。由于DW中的非零较小特征值为噪声信息,直接对DW求逆会加大噪声对特征提取结果的影响,使识别率降低。而Dα是通过减法运算获得的,减少了这些噪声大幅增大的机会。因此,可以认为Dα是比更稳定的估计。则可将SW的逆矩阵可表示为:

其中,Dα=λαI-Dw∈Rr×r为D-1W的估计矩阵。

根据式(7),可以将SB表示为:

结合式(10)和式(11),可以得到:

3.2 改进Fisher准则的应用

虽然3.1节的方法完整地包含了SW的列空间和零空间,但由于SW的求逆运算使它的较大特征值所对应的特征向量权重降到很低,因此没有充分利用SW的列空间信息,且丢弃了SB的零空间。为了更好地利用SW的列空间且包含SB的零空间信息,修改传统Fisher准则为:

其中:

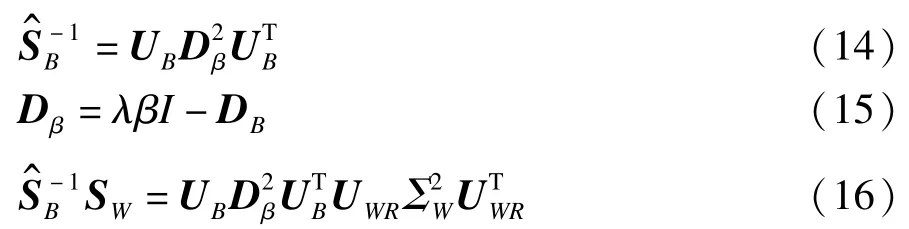
其中,λ≥1;β为SB的最大特征值;I为与DB相同维数的单位矩阵。

3.3 算法流程

该两级LDA方法的详细步骤如图1所示。

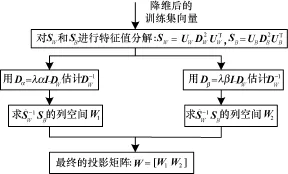
图1 两级LDA方法流程

4 实验结果与分析

本文实验的硬件环境为型号为Pentium E5300的CPU,主频2.6 GHz,软件环境为Visual Studio2010,采用OpenCV 2.3.4作为二次开发工具。实验对象取自ORL人脸数据库与YALE人脸数据库。ORL人脸库由40个人,每人10幅图像组成,图像的分辨率均为112×92像素,如图2(a)所示。YALE人脸库包含15个人,每人11幅人脸图像,为了便于处理,将图片大小剪裁成100×100像素,如图2(b)所示。本文从ORL人脸库中每人随机选取5幅,一共200幅人脸图像作为训练集,其余的图像作为测试集,从YALE人脸库中每人随机选取5幅,一共55幅人脸图像作为训练集,其余的图像作为测试集,分别在ORL和YALE人脸库上进行实验,同时与Fisherface、DLDA、RLDA算法进行识别率比较。

图2 一组人脸图像样本

4.1 参数对人脸识别率的影响

为了减少计算复杂度,采用2D-PCA方法对人脸图像进行预处理,以降低图像矩阵的维度。在2DPCA方法中,最佳投影轴数目(即Wopt中向量的个数d)与后期计算复杂度和人脸识别的准确率紧密相关。同时,在对样本的类内散度矩阵SW和类间散度矩阵SB的逆矩阵的计算过程中,需采用Dα=λαIDw和Dβ=λβI-DB分别估算D-1W和D-1B,通过3.1节的分析可得,参数λ应满足λ≥1。

为了探讨参数d和λ对人脸识别率的影响,令λ分别为1.0,1.5,2.0,5.0和9.0,分析投影轴数目d的变化时,本文算法对ORL、YALE人脸库中测试样本的识别率变化情况如图3所示。由图3可知,当d较小时,识别率较低,随着d的增大,识别率也在提高,但是d到达一定的值后,识别率便保持于一稳定状态。这表明图像的大部分鉴别信息集中于2D-PCA方法中较大特征值所对应特征向量的投影方向上,进一步增加投影轴数目不能提升识别率,且会导致计算复杂度大幅上升。对ORL人脸库,d=8时算法的性能最优;对YALE人脸库,d=6时算法的性能最优。

图3 投影轴数目d与参数λ对识别率的影响

当λ从1.0～9.0递增时,本文算法在ORL人脸库中的识别率均保持为92.5%,在YALE人脸库中的识别率均保持为95.8%。因此,只要保证Dα和Dβ中的元素根据DW和DB中的值保持升序排列,λ的取值对本文算法的识别率并无影响。所以,在之后的讨论中,均令λ=1。

4.2 特征维数对识别率的影响

W1主要包含了SB的列空间、SW的零空间信息,W2主要包含了SW的列空间、SB的零空间信息,因此,本文算法的最终投影轴W∈Rr×2rb包含了LDA的所有4个信息空间。理论上,所包含的鉴别性信息越多,人脸识别率就越高。因此,分析W的列向量个数D(即特征维数)变化时本文算法对ORL、YALE人脸库中测试样本的识别率变化情况。

对ORL人脸库,2rb=78,令D从6递增到78,识别率的变化情况如图4(a)所示,对YALE人脸库,2rb=28,令D从5递增到28,识别率变化情况如图4(b)所示。从图4中可以看出,随着特征维数的增加,人脸识别率也在提高,直到在一个定值上稳定下来。当D=rb时,ORL人脸库的识别率为91.2%, YALE人脸库的识别率为94.2%。D继续增加到2rb时,ORL人脸库的识别率增加到92.5%,YALE人脸库的识别率增加到95.8%。这说明了在LDA算法中,人脸的鉴别信息主要集中在SB的列空间和SW的零空间中,但SW的列空间和SB的零空间依然包含了对分类有用的信息,将它们包含进来确实可以提高识别率。

图4 特征维数对人脸识别率的影响

4.3 本文算法与常用LDA算法的性能对比

本文算法还与其他 3种常用 LDA算法Fisherface[6]、DLDA[7]和RLDA[9]进行比较。表1为上述算法与本文算法在ORL和YALE人脸库上的识别率对比结果,表2为上述算法与本文算法在ORL和YALE人脸库上的训练时间与识别时间对比结果,表中所列结果均在各算法的最优参数下所得。

表1 不同特征提取算法的识别率对比

表2 不同特征提取算法的训练时间与识别时间对比 ms

Fisherface采用PCA降维使类内散度矩阵非奇异,因而丢失了很多重要的鉴别信息。DLDA不但没有利用SW的列空间和SB的零空间,而且由于第一次降维之后空间维数太小,从而限制了其进一步获得具有更强判别力的投影方向。相似的,RLDA丢弃了SB的零空间,且没有充分利用SW的列空间,因而识别率也不理想。本文算法完整地利用了LDA的4个信息空间,因此与其他3种算法相比,具有最好的识别率的同时具有最长的训练时间,但每幅图像的识别时间只在2 ms的差距内浮动。

5 结束语

本文对人脸识别中常用的LDA特征提取算法进行了研究,提出一种基于2D-PCA的两级LDA人脸识别方法,解决了小样本问题,以及常用LDA算法没有完整利用LDA中4个信息空间而识别率不高的问题。在ORL和YALE两大人脸库进行实验,证明本文算法在提高识别率上的优越性。由于本文算法需要连续应用Fisher准则和修改后的Fisher准则来获取最优投影空间,在提高人脸识别率的同时也带来了额外的计算开销,因此在提高人脸识别率的基础上,降低算法的时间消耗,将是进一步的研究重点。

[1] Sharma A,Paliwal K K.A New Perspective to Null Linear DiscriminantAnalysisMethod and ItsFast Implementation Using Random Matrix Multiplication with Scatter Matrices[J].Pattern Recognition,2012,45 (6):2205-2213.

[2] Sharma A,Paliwal K K.A Two-stage Linear Discriminant Analysis for Face-recognition[J].Pattern Recognition Letters,2012,33(9):1157-1162.

[3] Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.Fisherfaces:Recognition Using Class Specific Linear Projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[4] Yu Hua,Yang Jie.A Direct LDA Algorithm for Highdimensional Data with Application to Face Recognition [J].Pattern Recognition,2001,34(10):2067-2070.

[5] 俞 冰,金连甫,陈 平.利用标准化LDA进行人脸识别[J].计算机辅助设计与图形学报,2003,15(3): 302-306.

[6] 宋晓宁,郑宇杰,杨静宇,等.对称零空间准则下的LDA特征抽取方法[J].计算机辅助设计与图形学学报,2009,21(3):400-405,411.

[7] 张燕平,窦蓉蓉,赵 姝,等.基于集成学习的规范化LDA人脸识别[J].计算机工程,2010,36(14):144-146.

[8] Guo Yaqian,Hastie T,Tibshirani R.Regularized Linear Discriminant Analysis and Its Application in Microarrays [J].Biostatistics,2007,8(1):86-100.

[9] Sharma A,Paliwal K K.Regularisation of Eigenfeatures by Extrapolation of Scatter-matrix in Face-recognition Problem[J].Electronics Letters,2010,46(10):682-683.

[10] Gao Hui,Davis J W.Why Direct LDA is not Equivalent to LDA[J].Pattern Recognition,2006,39(5):1002-1006.

[11] Paliwal K K,Sharma A.Approximate LDA Technique for Dimensionality Reduction in Small Sample Size Case [J].Pattern Recognition Research,2011,6(2):298-306.

[12] Yang Jian,Zhang D,Frangi A F.Two-dimensional PCA:A New ApproachtoAppearance-basedFace Representation and Recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004, 26(1):131-137.

编辑 任吉慧

Two-stage Face Recognition Method Based on Two Dimension Principle Component Analysis

WANG You-zhao1,PAN Fen-lan1,HUANG Jing2
(1.Institute of Digital Technology and Instrument,Zhejiang University,Hangzhou 310027,China;
2.School of Informatics and Electronics,Zhejiang Sci-Tech University,Hangzhou 310018,China)

Aiming at the existing algorithms which do not use the whole four information space of Linear Discriminant Analysis(LDA)in solving the small sample size problem,a two-stage LDA face recognition algorithm based on Two Dimension Principle Component Analyses(2D-PCA)is proposed.The small sample size problem is solved by a subtraction to estimate the inverse matrix of the eigenvalues matrix of the singular with-class scatter matrix and betweenclass scatter matrix.Thus,the projection subspaces resulting from continuously using the traditional Fisher criterion and a modified Fisher criterion,are concatenated to obtain the optimal projection space including whole four information space of LDA.To reduce the computational complexity,the 2D-PCA is used to preprocess on input samples.The recognize rates of the proposed algorithm on ORL and YALE database are 92.5% and 95.8% which are higher than other LDA algorithms despite the slightly increase of training time.

Linear Discriminant Analysis(LDA);Direct LDA(DLDA);Two Dimension Principle Component Analysis(2D-PCA);small sample size problem;face recognition;feature extraction

1000-3428(2014)09-0243-05

A

TP18

10.3969/j.issn.1000-3428.2014.09.049

王友钊(1963-),男,副教授,主研方向:图像识别,机器视觉,噪声主动控制,智能电网技术;潘芬兰,硕士研究生;黄 静,教授。

2013-08-22

2013-09-29E-mail:wangyouzhao@zju.edu.cn