两点法误差分离技术的分离精度分析

母德强，谢新旺，崔博，陈懿

(长春工业大学机电工程学院，吉林长春 130012)

近年来，随着高精度机械加工技术的不断发展，对零件形位误差要求也在不断地提高。为了保证被加工工件的形位精度要求，在线测量是首选的检测方法。而由于加工系统中存在着许多不可预测的影响因素，使得工件形位误差的在线测量变得十分困难，误差分离技术 (Error Separation Technique，EST)的出现为形位误差的在线测量提供了可能［1］。

误差分离技术 (EST-Error Separation Techniques)于20世纪五六十年代发展起来，历经国内外三十余年的研究，现在已经有了很强大的理论基础和很丰富的内容。通过一些学者的不断努力，误差分离技术现在有很广泛的发展。比如:根据是否使用傅里叶变换可以把误差分离技术分为频域法误差分离技术和时域法误差分离技术;根据使用传感器个数可以分为反向法误差分离技术、两点法误差分离技术、三点法误差分离技术、四点法误差分离技术等［2］;根据检测形状的不同又分为圆度误差分离技术、直线形状误差分离技术等。

在众多的误差分离技术中，频域两点法误差分离技术用于在线检测时仅使用两个传感器，因方便安装而倍受青睐。不过其缺陷是:该方法无法完全分离零件的偏心误差，分离结果含有误差。此外两点法误差分离技术的分离结果的误差规律还没有一个明确的规则。因此对两点法误差分离技术尚无一个客观的分析。作者正是基于此而进行探索，旨在从理论分析与实践上进一步探索两点法误差分离技术原理误差的影响因素及影响规律，力求提高两点法误差分离技术在线测量的精度问题。

1 两点法误差分离技术的测量原理

两点法误差分离技术由三点法误差分离技术发展而来的。因为两点法误差分离技术用到了傅里叶变换，因此两点法误差分离技术又称为频域两点法误差分离技术。频域三点法误差分离技术的原理图如图1所示。

图1 频域三点法误差分离技术的原理图

图中，O为传感器A、B和C所在位置处的位移敏感中心线的交点，也为该转轴的实际回转中心。但是该截面的最小二乘圆心为O0，与实际回转中心O的偏心距为e。以点O为坐标原点建立坐标系，x轴的正方向为从回转中心O指向传感器A，并通过其中心线;y轴的正方向为从回转中心O指向传感器B并通过其中心线，垂直于x轴。

设h(θ)为工件的圆度误差，δx(θ)、δy(θ)为主轴回转运动误差在x、y上的分量;传感器之间的夹角如图1所示［3］。所以，3个传感器的输出为

为了消除各传感器输出中的回转误差分量，对等式 (1)— (3)乘以不同的等权常系数1、a、b然后相加，得到的方程为

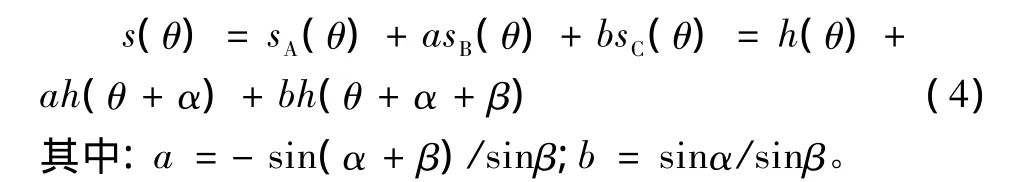
为了能更好地使用傅里叶变换，在进行测量时等间隔地在被测件每一周上采集的点数N=2n。并有

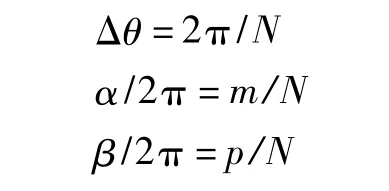
式中:m、p都为正整数，那么等式 (4)的离散形式可以写为

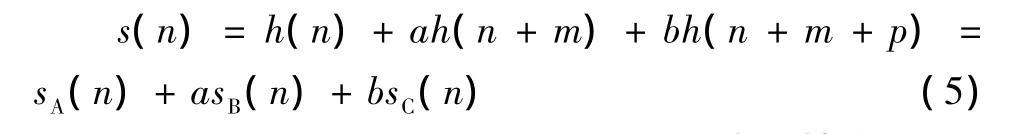
取m=N/4，p=m-1，γ=Δθ。则N越大，α+β→180°，a越趋近于0。当N大于某一数值之后，可认为a=0。此时传感器B就可以忽略，三点法误差分离技术就转化成了两点法误差分离技术。

因此等式 (5)可以化为

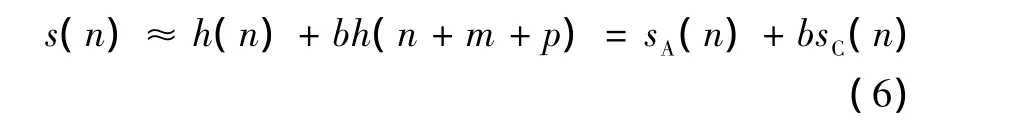
因为sA(n)、sC(n)都为所测得的已知量，因此，等式 (5)作离散傅里叶变换，根据傅里叶变换的时延相移特性可得

在等 式 (7) 中:S(k)=DFT［s(n)］;H(k)=DFT［h(n)］;G(k)=1+bej2π(m+p)k/N。

由h(n)=DFT－1［H(k)］=DFT－1［S(k)/G(k)］，就可求出被测工件的圆度误差h(θ)的离散形式h(n)。

2 影响两点法误差分离技术的因素

通过两点法误差分离技术的原理可知，该误差分离技术存在原理误差。影响频域法误差分离技术精度的主要因素有:采样误差，即采样点数的影响;谐波抑制;传感器的安装角度误差和一些随机的干扰噪声等［5］。

因为随机的噪声等干扰因素无法预测，也不可能消除，只能通过求多组的平均值来尽可能地减小，因此文中只讨论其余几种因素的影响。

2.1 谐波抑制对两点法误差分离技术的影响

在三点法误差分离技术中应用傅里叶逆变换时，不论参数m、p、α、β如何取值，都有G(1)≡0，常用的处理方法是令S(1)=0。在傅里叶逆变换时，该位置的谐波分量就因为置0而损失［4］，从而引入谐波抑制现象。为了避免谐波抑制，令G(1)=1［5］。然后在进行傅氏逆变换就可以得到被测工件的圆度误差h(θ)的离散形式h(n)。

但是，在两点法误差分离技术中

所以G(k)≠0恒成立，k∈(0，N-1)。所以两点法误差分离技术中不存在谐波抑制现象。

2.2 采样点数对两点法误差分离技术的影响

通过两点法误差分离技术的原理可知，传感器B所采集序列在进行消除回转误差时的常权系数a=-sin(α+β)/sinβ。当N增大时会使得α+β→180°、a→0，但并不等于0。在其他条件都正确的条件下，忽略传感器B就无法完全消除主轴回转运动误差。因此该原理误差取决于a［δx(θ)cosα +δy(θ)sinα］的大小。

2.2.1 当主轴不存在偏心误差时

当转轴不存在偏心误差时，即e0=0，则δx=δy=0。

因s(θ)=h(θ)+h(θ+α+β)，所以S(k)=H(k)(1+ej2π(m+p)k/N)=H(k)G(k)， 那 么h(θ)=FFT－1(H(k))=FFT－1(S(k)/G(k))是精确值。

由此可知，在传感器安装正确时若回转轴无偏心误差，只要采样点数满足傅氏变换的要求和采样定理，通过两点法所求出的圆度误差都是精确的。

2.2.2 当主轴存在偏心误差e0时

设aN、αN、βN和γN分别为当采样点数取N时参数a、α、β、γ的值，则有

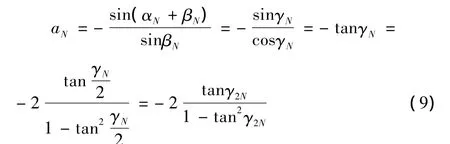
因γN=2π/N，所以采样点数N越大，角度γN越小，tan2γN越趋近于0。因此

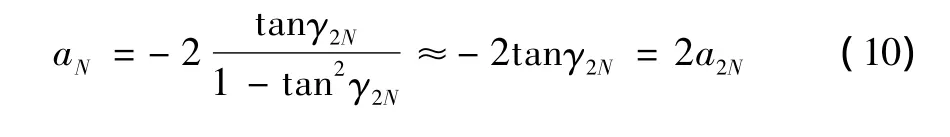
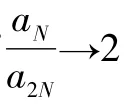
2.3 安装角度对两点法误差分离技术的影响

因为γN=2π/N，当采样点数N过大，会使夹角γN过小，从而给传感器C的安装带来困难。当传感器C的安装角度不精确时，也会给分离结果带来误差。

在安装传感器C的时候，设角度α+β的安装角度误差为Δφ，则

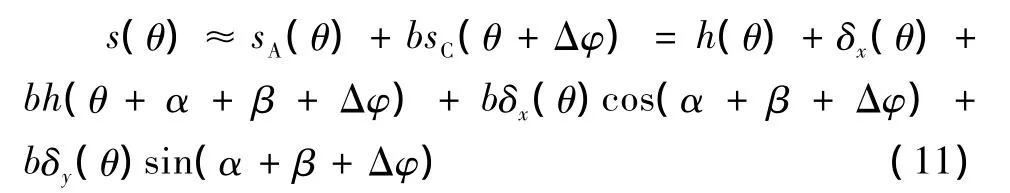
又因 δx(θ)=e0cosθ，δy(θ)=e0sinθ，α+β=π－γ，则

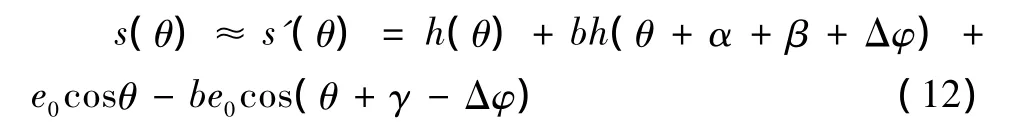
对式 (12)作FFT得

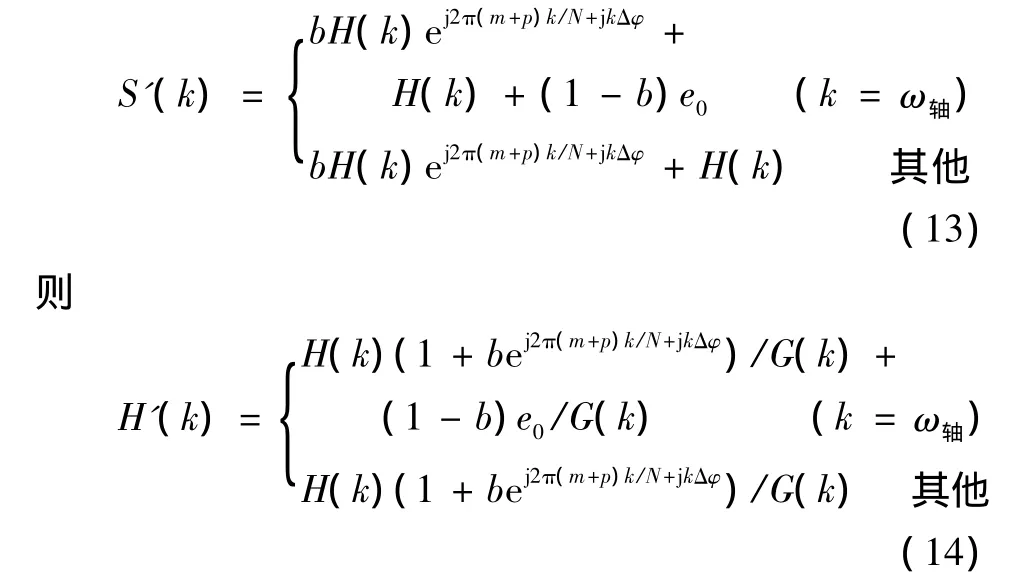
对式 (14)作逆FFT是十分困难的，由傅氏变换的线性性质得［6］

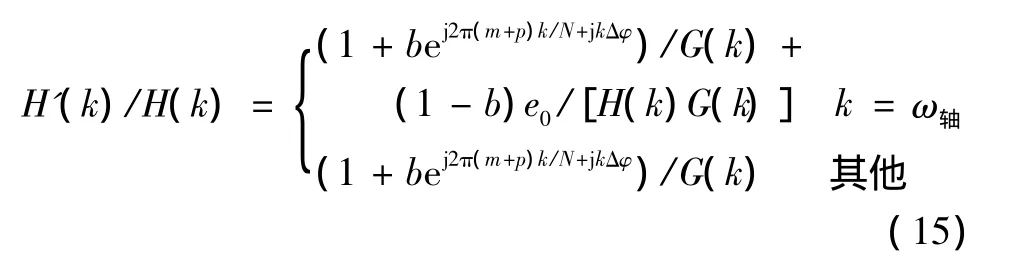
2.3.1 当e0=0，即转轴不存在偏心误差时

H'(k)/H(k)=(1+bej2π(m+p)k/N+jkΔφ)/G(k)，由欧拉公式把该式进一步化简得

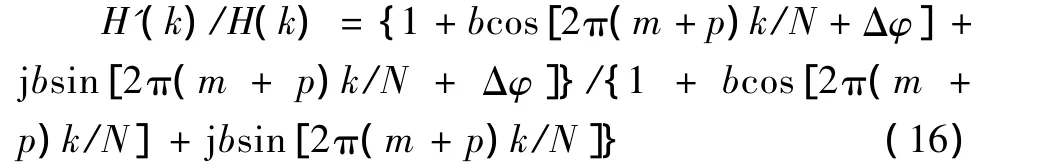
令ψ=2π(m+p)k/N;把式 (16)分母实数化，取分子的模的平方可得

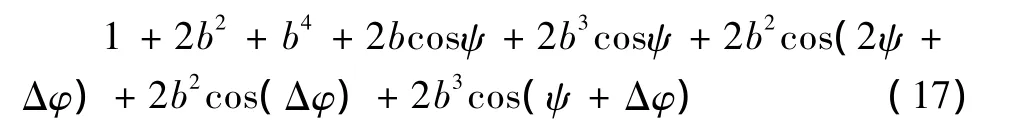
对式 (17)求导得

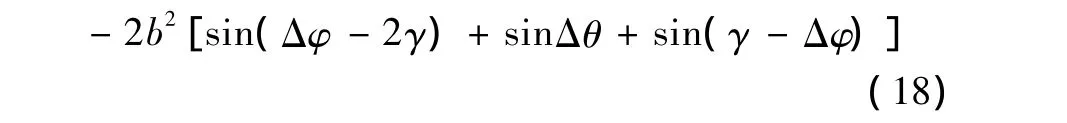
通过式 (18)可以得，当Δφ从 ［0，γ］增大时，导数大于零;从 ［γ，2γ］增大时，导数小于零。所以当Δφ=γ时，即2π (m+p)k/N+Δφ=2π时h'(θ)的误差最大。

2.3.2 当e0≠0，即转轴存在着偏心误差时

由式 (13)可以看出，当对s(θ)求傅氏变换之后，偏心距对精度的影响与角度误差Δφ无关，因此只能在傅氏变换之前讨论安装角度误差Δφ对误差分离精度的影响。

只考虑偏心部分对叠加信号的影响，令

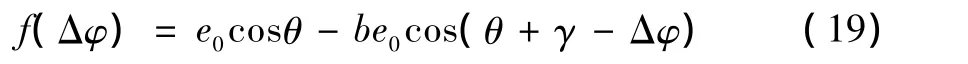
当该等式取最小值时，引入的误差最小。对上式求导得f'=-sin(θ+γ-Δφ)。分析该等式可知当(θ+γ-Δφ)∈(0，π)时，该角度误差使圆度误差值减小，(θ+γ-Δφ)∈(π，2π)角度误差使圆度误差值增大。

证明了对置安装两个传感器时，有利于消除转轴的偏心误差。

3 理论验证两点法误差分离技术的误差分析

为了检验上述的分析，作者进行了如下的仿真验证。

3.1 采样点数对两点法误差分离技术精度的影响

在该验证实验中，取基本半径尺寸为20 mm、表面上有4组振幅为3 mm的正弦所叠加而成的轴。保证除采样点数N除外的一切条件不变，N的取值为16、32、64、128、256、512、1 024、2 048。分别采集这几组信号，分别对这些数据进行分析，可得如表1所示的结果。

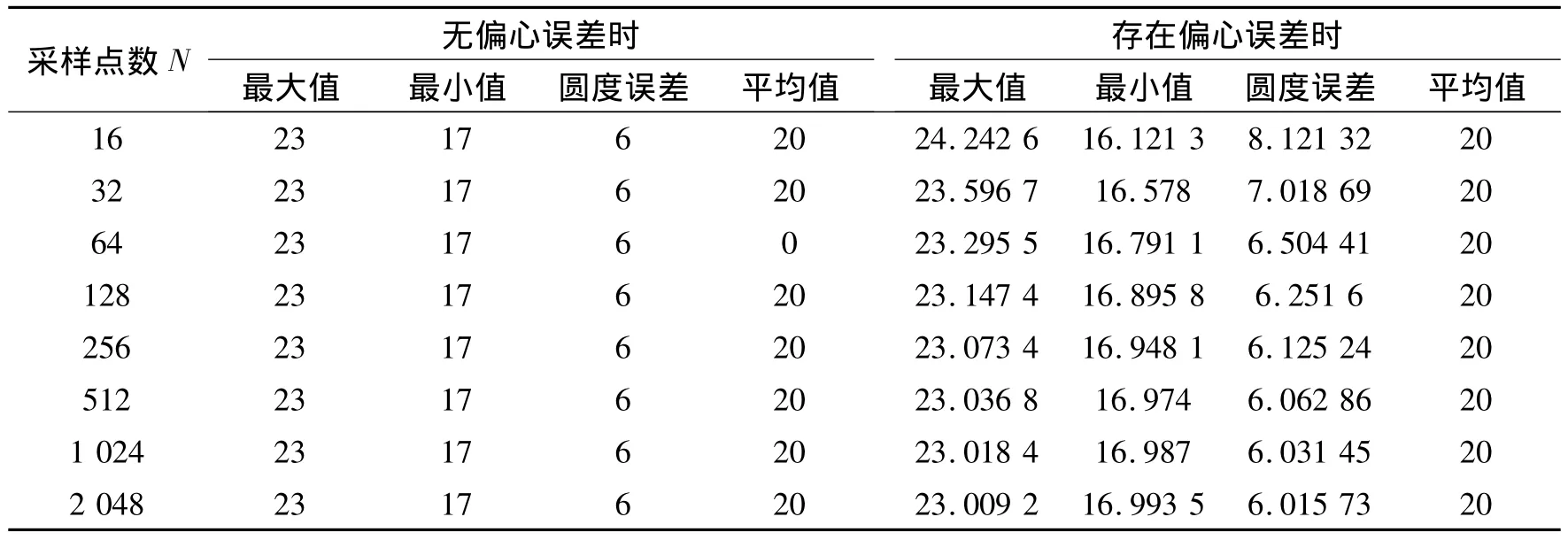
表1 采样点数N对两点法误差分离精度的影响的验证 mm

通过理论分析可知，最大值、最小值、圆度误差和平均值的实际理论值分别为23，17，6，20。仔细的观察该表可以看出:当转轴不存在偏心误差时，两点法误差分离技术的分离结果与理论值相等;当转轴的偏心误差e0≠0时，各量的绝对误差值随着采样点数N的增大而减小，且减小的倍数越来越接近于2，证明了采样点数对误差值的影响规律的理论分析是正确的。

3.2 安装角度误差对两点法误差分离技术精度的影响

在检测安装角度对分离误差带来的影响时，选取的采样点数N=256，所以理论上α+β的度数应该为178.593 75°。为了分析安装角度的影响，令安装角度α+β的值从174.6°到180.6°等间隔变化，间隔为0.2°，除此之外保证其他参数不变。

在检验的时候对有偏心误差和无偏心误差同时分析。分析时的数据为:被测件基本半径为20 mm，表面上有振幅为3 mm的正弦信号。当有偏心时偏心距取3 mm。分离结果如图2所示。

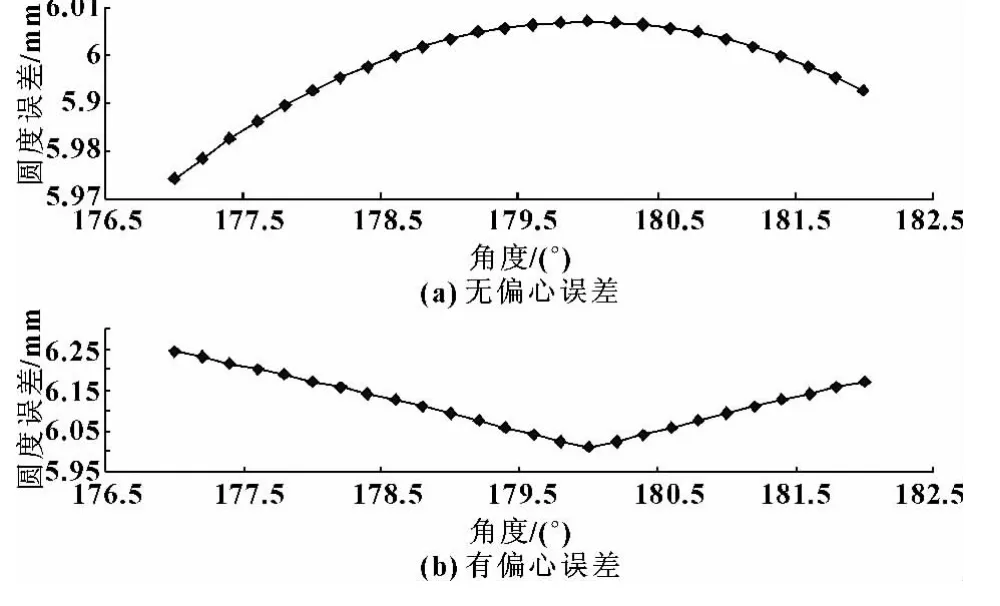
图2 安装角度误差对圆度误差的影响

观察图像可以看出:在以理论安装角度为中心的一个区间范围内，无偏心误差时随着安装角度的增大，分离误差会减小，不过在180°的位置达到极值并且关于180°对称;存在偏心误差时，随着安装角度的增大，分离误差随着安装角度的增大而减小，也在180°的位置达到极值并且关于180°对称。证明了第2.3节中的分析和推导是正确的。

4 试验验证

通过上面的仿真分析验证了影响两点法误差分离技术误差的因素及其影响规律符合理论分析。作者在实验室环境内通过实验来进一步验证理论分析与仿真分析。

实验所用设备为:通过磨削加工一个长度280 mm、直径为50 mm的轴进行试验验证;传感器采用的是德国米铱的NCDT系统控制的单通道精密电容位移传感器CapaNCDT620［7］。进行测量时，分别取采样点数N=64、128、256、512，则安装角度α+β=(1-2/N)π。为了减小检测过程中的随机误差，对工件反复测量5遍取平均值。测量结果如表2所示。通过该试验结果可以看出:频域两点法圆度误差分离技术的分离结果与理论分析和仿真验证相符，证明了在使用两点法误差分离技术时，主轴含有偏心误差那么对置安装两传感器可以得到更高的精度。因此说明了频域两点法误差分离技术在要求一定精度的场合下也可以满足检测要求。

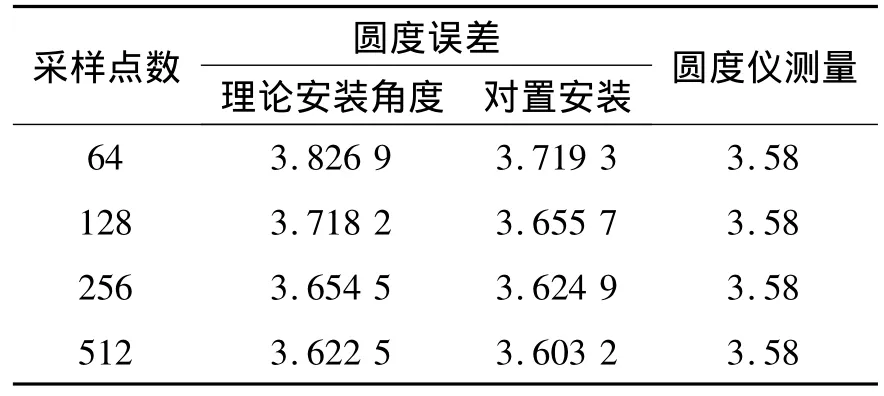
表2 实验分离结果 μm

5 结论

(1)当使用两点法来进行误差分离时，若被测件不含有偏心误差，对置安装传感器会使分离出的圆度误差的误差最大;若被测件含有偏心误差，对置安装传感器会使分离值的误差最小;(2)在现实的加工过程中几乎所有的转子都存在着偏心误差，因此检测时我们一般采用对置安装传感器可以得到更精确的圆度误差值;

(3)两点法误差分离技术虽然有原理误差，但是仍比反向法误差分离技术的精度高。在规定精度要求下仍然可以使用。

［1］张镭，赵莹，张玉.三测头法误差分离技术的理论与试验［J］.机械工程学报，2009，45(6):256-261.

［2］徐可伟，朱训生，陈正昕.几种常用圆度误差分离方法的分析及比较［J］.计量技术，2000(8):26-28.

［3］洪迈生，邓宗煌.圆度和回转运动的时域二点法分离技术［J］.中国机械工程，1997(8):88-89，92.

［4］李超.基于误差分离技术的精密回转及直线运动部件精度测量［D］.哈尔滨:哈尔滨工业大学，2010.

［5］黄建健.基于频域三点法的主轴回转误差测量方法与应用研究［D］.广州:广东工业大学，2011.

［6］李济顺，洪迈生.三点法圆度误差分离的近似方法及精度分析［J］.计量技术，1998(2):8-11.

［7］母德强，李晓迪，丁宁.一种曲轴轴径圆度误差测量系统［J］.长春工业大学学报，2010，31(3):300-304.

［8］丁曙光，李浩，桂贵生.三点法圆度误差分离技术在轴类零件测量中的应用研究［J］.机床与液压，2008，36(2):116-118.

［9］雷贤卿，李言，周彦伟，等.3点法圆度误差分离技术的新算法［J］.兵工学报，2007，28(1):73-77.

［10］刘逸飞，邹雪妹，谈理.基于误差分离技术的圆度自动检测的研究［J］.机械设计与制造，2013(2):147-149.

［11］张军峰，王燕燕.EST法测量机床导轨直线度误差分析［J］.机床与液压，2010，38(3):46-49.