型砂压实过程的非线性有限元数值模拟
李文珍,吴浚郊,周克林
(1.清华大学材料学院,北京 100084;2.上海汽车集团,上海 200041)
在湿型砂铸造生产中,为了保证铸件的几何尺寸和力学性能符合设计和使用要求,高质量砂型的生产起决定作用。型砂紧实过程是生产砂型的关键工艺环节,利用现代模拟仿真技术对型砂紧实过程进行模拟,预测砂型紧实度分布并进而预测砂型质量,是提高造型生产效率获得高质量铸型的有效手段。但是黏土湿型砂属于离散材料体系,与一般的连续材料体系相比具有如下特点:
1)材料非线性即砂型由大量非连续的外层包覆黏土-水膜的细小砂粒组成,砂粒间相互接触;
2)几何非线性即型砂在紧实过程中砂型的变形量很大,可达30%以上;
3)接触非线性即在紧实过程中型砂与砂箱和模样之间存在非线性接触。因此在型砂紧实过程中同时存在着材料非线性、几何非线性和接触非线性,这类问题一般用非线性有限元法进行求解,如图1所示。目前所能查到的湿砂造型数值模拟领域最早的研究是Leone和R.L.Lewis[1]使用有限元法对压实造型中型砂密实过程进行的数值模拟。
1 用ANSYS软件求解非线性问题方法简介
ANSYS软件是一个商品化的大型通用有限元分析软件,目前广泛应用于土木工程、水利工程、机械工程、航空航天和汽车交通等领域。ANSYS具有一些突出的技术特点:将前处理模型的信息(单元、节点、材料),边界条件(载荷、约束)以及后处理信息(求解结果)集成在统一的数据库中,极大地方便了用户的使用。ANSYS具有强大的非线性分析功能,可以处理几何非线性、材料非线性、状态非线性及单元非线性问题。ANSYS提供了100余种非线性材料模型如橡胶、泡沫、土壤和岩石等。另外ANSYS软件能够灵活地在前处理中进行网格划分,确保了单元的形态和精度。用ANSYS软件求解非线性问题需要一系列带校正的线性近似来实现,如图2.

图1 型砂压实过程中非线性问题的求解流程

图2 纯粹增量近似与牛顿-拉普森近似的关系[2]
ANSYS软件使用牛顿-拉普森平衡迭代进行计算,它迫使在每一个载荷增量的末端解达到平衡收敛(在某个容限范围内)。图2b)描述了在单自由度非线性分析中牛顿-拉普森平衡迭代的使用。在每次求解前,NR方法估算出残差矢量,这个矢量是回复力(对应于单元应力的载荷)和所加载荷的差值。程序然后使用非平衡载荷进行线性求解,且核查收敛性。如果不满足收敛准则,重新估算非平衡载荷,修改刚度矩阵,获得新解。持续这种迭代过程直到问题收敛[2]。
ANSYS程序提供了一系列命令来增强问题的收敛性,如自适应下降,线性搜索,自动载荷步,及二分等,可被激活来加强问题的收敛性,如果不能得到收敛,那么程序依据输入的命令或者继续计算下一个载荷前或者终止[2]。
2 型砂材料本构关系建立
型砂本构关系即应力应变关系的建立是对砂型紧实过程进行有限元分析的基础。在土力学中已提出了很多测定和建立砂土本构关系的方法,主要实验方法为有侧限压缩,它是目前最常见的用来测量土的压缩性能的试验方法[3]。
2.1 型砂本构关系测试原理[4]
图3所示为型砂静态本构关系测试原理。具体方法是:将混好的型砂加入试样筒中,随后利用液压式万能试验机进行慢速加载,通过试样上的压板作用在松散的型砂表面。在加载过程中,压杆上的BLR-1载荷传感器测量压板载荷P的变化,位移传感器测量压板相应的位移值U。这两路传感器信号经Y6DL-1型应变仪放大后,由LZ3-304函数记录仪以P为纵坐标,U为横坐标输出P-U曲线。经下列转换得到在静态载荷作用下,有侧限情况下的型砂应力-应变(本构关系)曲线。

式中:S-压板面积;
h-试样筒的高度。

图3 测量型砂静态本构关系实验原理图[4]
2.2 试验结果及分析
取型砂紧实率40%,膨润土含量为10%,初始密度分别为 0.9g/cm3、1.0g/cm3、1.1 g/cm3、和 1.2g/cm3,测得的型砂应力应变关系如图4所示。
从图4可以看出型砂应力应变关系为非线性,呈下凹形状,这点与大多数连续材料的特性不同。未紧实的松散型砂在整个压缩过程中具有非常大的变形量。其原因如下:型砂在开始受压时的变形主要表现为砂粒重新排列填补空隙,因此应力较小;当型砂紧实到一定阶段,砂粒之间的接触变得更加紧密,砂粒运动不仅需要克服黏土膜之间的黏滞力,还要克服砂粒之间的摩擦力;在紧实的最后阶段,砂粒之间石英内核发生相互作用的正应力,因为石英颗粒非常坚硬,所以紧实后期应力急剧增大。
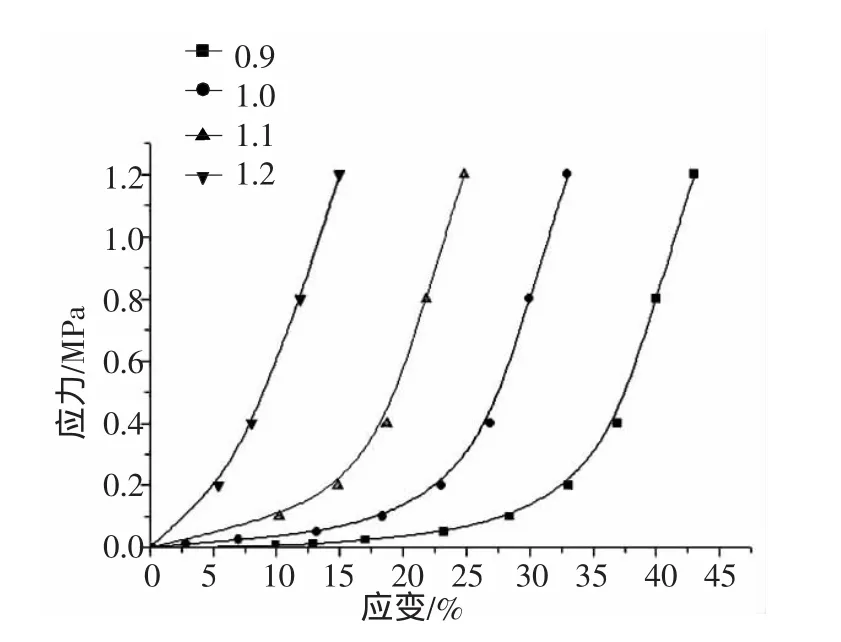
图4 型砂本构关系曲线
3 型砂压实过程的数值模拟
在获得型砂侧限条件的本构关系后,本文在有限元软件ANSYS的平台上,采用APDL进行二次开发,编写了相应的计算程序并耦合到现有ANSYS软件中,对型砂压实过程进行了数值模拟。
3.1 材料模型的建立
从上述型砂本构关系试验结果可以看出,型砂的本构关系是一种非线性应力应变关系,其应力对应变的一阶导数即弹性模量在变形过程中随着应变的增加而递增,对于这样的模型,通常的商业分析软件无法直接予以处理,必须对实际本构关系进行一定的简化处理,并采用APDL语言进行编程来完成计算,以实现对这种复杂应力应变关系的求解。
本文根据型砂材料的实际特点,对型砂材料模型作了如下假定:
1)型砂是均匀、连续、各向同性的介质;
2)由于型砂紧实过程相对较快,因此,计算过程中不考虑回弹;
3)应力加载过程为从零单调增加到最大,卸载过程为无位移(很小)回弹。根据这些假定,对试验测得的型砂非线性本构关系(图4)采用多线性本构关系进行简化,如图5所示。在曲线上,每两点之间为一直线段,弹性模量ΔE=Δσ/Δε为常数,型砂表现为线弹性材料。本文选取了初始密度为0.9 g/cm3,膨润土含量为8%,紧实率为40%的型砂作为计算对象,线性段阶跃点的应力应变值如表1所示。
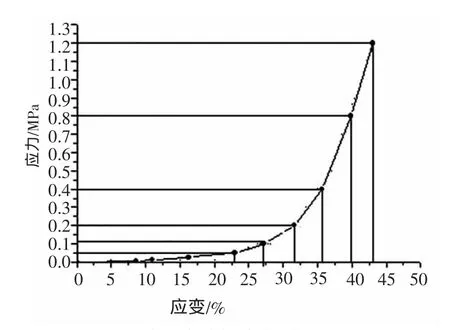
图5 型砂的多线性本构关系

表1 初始密度为0.9 g/cm3的型砂各线性段应力应变
3.2 型砂几何模型
计算中,型砂几何模型如图6所示。设砂箱和余砂框的总高度为A,压实后型砂顶面距离分型面的高度为B,未压实前成型压头距离模样顶面的距离为a,压实后型砂定面距离模样顶面的距离为b.为了使型砂压实后型砂更加均匀,则成型压头尺寸满足以下等式条件:


图6 几何模型尺寸
3.3 加载过程和边界条件的处理
在型砂压实过程中,型砂与砂箱之间存在很大的摩擦力,这对型砂压实过程有着不可忽略的影响,因此在计算过程中,在砂箱和型砂之间采用接触条件,并参考文献[3]中的数据,取平均摩擦系数为0.5.
由于型砂和砂箱之间存在摩擦力,型砂采用单面压实后,紧实度分布情况一般为上紧下松,这对于处在分型面处的型腔在充填金属液体时是极为不利的。因此,本文分别计算了两种加载情况:
1)采用上加压单面压实;
2)采用上下加压双面压实,且按照上面加载量为下面加载量的3倍进行加载,并比较了两种加载情况的计算结果。本文计算了紧实率为40%,膨润土含量为8%,初始密度为0.9 g/cm3的型砂。采用位移加载,且按照压缩40%的位移量加载;由于型砂的本构关系特殊,将型砂分为几个线性段进行近似模拟,采用分步加载。在加载过程中,根据每个线性段的弹性应变量进行分步位移加载。当前一个分步加载求解完毕后,提取计算结果并改变模型中各个节点的位置,重新划分网格,然后改变弹性模量,在进行下一个分步加载求解时,将前一个分步计算的结果以预应力载荷加在重新划分网格的模型上,重复该计算过程,直到计算求解到最后一个线性段结束为止。
单元采用8节点平面等参元,初始网格划分结果如图7所示。由于型砂在压实过程中具有流动性特征,若以弹性材料进行求解,用ANSYS求解后会在成型压头附近出现一个缺口,为了解决此问题,将成型压头下面的节点在Y方向的位移进行耦合求解。此外,成型压头两边的型砂变形量大,单元若太小,在计算过程中容易发生不收敛而导致计算中止,因此特意将成型压头两边的型砂单元划分的较大,由于我们感兴趣的区域为分型面附近的应力分布,因此在型砂顶面将单元划大对结果不会有很大的影响[5]。

图7 模型网格划分结果
4 数值模拟结果及分析
4.1 单面压实和双面压实数值模拟结果的比较
数值模拟结果如图8a)和图b)分别是单面压实和双面压实后的计算结果。为了比较两种加载情况的计算结果,每一种加载情况都提取了两条线上的应力分布(如图6):一条靠近砂箱边缘,一条则为模型的对称中心线,两条线方向均由下向上。两条线上的应力值如表2和表3.将表中的应力制成图,如图9所示。

表2 沿砂箱边缘高度方向的应力分布各点的值

表3 沿砂箱中心线高度方向的应力分布各点的值
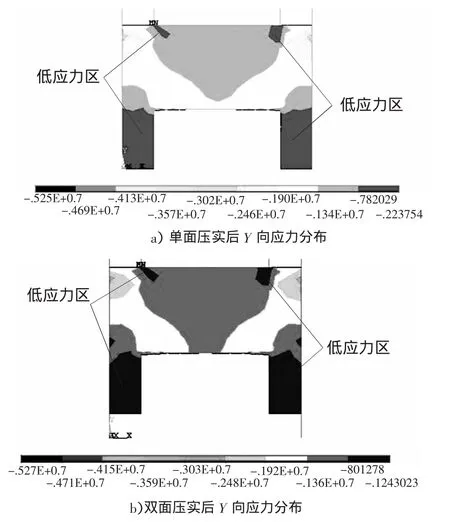
图8 数值模拟应力场的分布

图9 沿砂箱边缘和模型中心两条线上的应力分布
从图8和图9的模拟计算结果可以看出,由于型砂砂粒之间摩擦力及型砂与砂箱壁和模型表面之间摩擦力的影响,在靠近砂箱的附近应力沿砂箱高度方向增加(如图9),而在砂箱中心线附近应力则是沿砂箱高度降低(如图9),模拟结果符合实际紧实情况。同时值得注意的是,在模样拐角处和型砂狭窄区域入口处,应力场为颜色较深,表明在该处出现一个低应力区域,应力低于其上方区域的应力,模拟出了文献[4]试验中的“搭桥”现象。
此外从图9还可以看出,在高度较低的地方,双面压实砂箱边缘应力曲线的值要比单面压实砂箱边缘应力曲线的值要大;而在高度较高的地方,双面压实砂箱边缘应力曲线的值反而要比单面压实砂箱边缘应力曲线的值要小。由此说明,双面压实后,可以提高分型面处型砂的紧实度,且整个型砂应力分布要更加均匀,符合双面压实要优于单面压实的规律。
4.2 数值模拟结果和实验测量值的比较
由于实验条件所限,本文参考了文献[4]中的试验数据(如图10所示,图中应力单位为MPa),并将模拟结果与之作了数量级上的比较以验证模拟结果。

图10 参考文献[4]的实测应力分布图
文献[4]中的试验条件如下:砂箱平面尺寸为390 mm×350 mm,型砂初始密度为0.9 g/cm3,紧实率40%,膨润土含量为8%。这些试验条件除了砂箱尺寸和本文计算模型有一定的差别(本文模型尺寸为400 mm×300 mm),其他条件均相等,因而有一定的参考意义。
图9中计算出的沿砂箱高度方向的应力曲线和图10b)实测应力曲线非常相似,趋势相同,应力均随着高度的增加而增加,且都在砂箱和模样之间存在一块应力比较小的区域,也即“拱桥效应”。在应力值的数量级上,在“拱桥效应”区域,计算出的应力值大约在0.34 MPa~0.9 MPa之间,实测的应力值在0.36 MPa~0.7MPa之间;而在高出模样的区域,计算出的应力值大约在0.9 MPa~1.9 MPa之间,而试验测得的值也在0.8 MPa以上。此外,从计算结果和试验结果可以看出,在模样上方都有一块比较紧实的区域。上述结果表明数值模拟的结果和试验结果比较吻合。
5 结论
利用商品化有限元分析软件ANSYS,通过APDL二次开发编程对黏土砂造型的压实过程进行了数值模拟。通过对两种加载方法的计算结果比较以及计算结果与相应的试验数据比较,结果表明ANSYS可以很好地解决型砂紧实这样的非线性问题。湿型砂压实过程的数值模拟结果可以较好地解释如下现象:
1)“拱桥效应”现象;
2)“双面加压”要优于“单面加压”,从而可以提高型砂分型面的强度;
3)在砂箱边缘应力分布从下至上逐渐变大。
通过ANSYS软件对型砂紧实过程进行数值模拟取得了较好的效果。但是,由于实验数据来自参考文献,因而以后需要通过进一步的实验来验证模拟结果的精度。此外,本文模拟仍局限在二维模型上,对于三维模型模拟有待进一步的开发。
[1]Leone M,Lewis R L.Numerical Modeling of Green Sand During Compaction[J].AFSTransactions,1988,136:763-774.
[2]王国强.实用工程数值模拟技术及其在ANSYS上的实践[M].西安:西北工业大学出版社,1999.
[3]张翼飞.射压造型的数值模拟和试验研究[D].北京:清华大学机械工程系.2001.
[4]谢滨.压实造型和空气冲击造型砂型应力场研究[D].北京:清华大学机械工程系,1993.
[5]Li Wenzhen,Wu Junjiao.Numerical Simulation of Compacting Process of Green Sand Molding Based on Sand Filling[J],Materials Science Forum,2007,561-565:1879-1882.

