Poisson方程外问题平方收敛的不重叠Schwarz交替法
董永新, 王寿城
(合肥工业大学 数学学院,安徽 合肥 230009)
0 引言
文献[1-2]讨论了半平面上不重叠Schwarz交替法,利用极值原理证明了其在极大模意义下的几何收敛性;文献[3]讨论了一个双调和方程两子区域上无重叠的区域分裂法;文献[4]引入松弛因子加速Schwarz交替法收敛速度,论述了径向基函数配点法和不重叠型Schwarz交替法的结合用于求解椭圆方程。总之,解无界区域椭圆边值问题,常用有限元与边界元耦合法,做适当的人工边界,有限区域上用有限元方法,无界区域上用自然边界归化,从而有效地解这类方程。上述方法都是在某一解答过程中创新了一种方法的优良算法[5]。本文在原算法基础上离散二分迭代函数,从二分算法迭代值角度,以Poisson方程外问题为例,讨论二分迭代后新算法的加速收敛性质,数值算例和图像表明该平方收敛算法的优越性。
考虑Poisson方程外问题:

其中,Γ0={(r,θ)|r=a,a>0,},θ∈[0,2π]。构造人工边界Γ1={(θ,φ)|θ=β,β>0},Γ0的外部与Γ1的内部为Ω0,Γ1的外部为Ω1。
引理1 设投影算子是v到子空间vi的算子[6]:v→vi,i=0,1,V=V0+V1,对∀v∈V,存在a∈[0,1],使得:
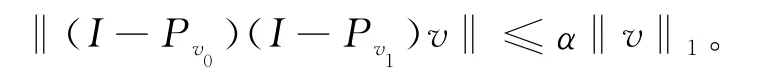
1 离散算法的实现及其误差分析
与(1)式对应的变分问题为:求u∈H1(Ω),使a(u,v)= (f,v),对 ∀v∈H1(Ω),数值分析基本思想是将连续问题离散化、离散问题连续化,此处将连续问题离散化,构造人工边界时,若Γ0为长条型区域,则取椭圆形人工边界[7-9]。
算法1 平方收敛不重叠Schwarz交替法[1]。问题(1)的泛函记为:

定理1 算法1将问题(1)解的误差收敛较原来以平方速度收敛,误差满足:
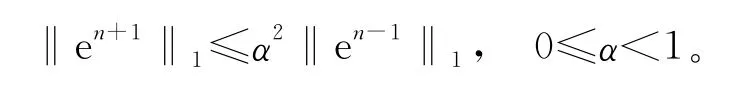


算法1相比于不重叠Schwarz交替法具有几何平方收敛性。Ω1上用自然边界元方法,因边界充分光滑,文献[10]推得(1)式的解的直接边界积分表达式为:
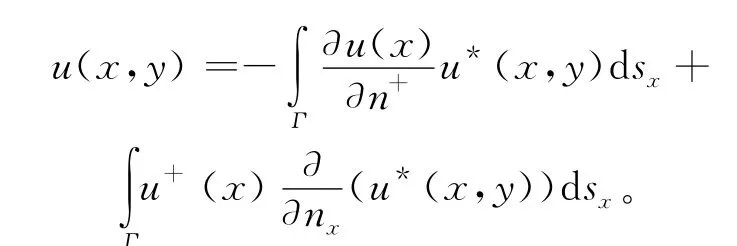
进行算法1的有限元模拟,先对Ω1作正则三角形剖分,Pi(i=1,2,…,N)为内结点,Qi(i=N+1,N+2,…,N+M)为边界结点,即Ω0h上的线性元空间为Sh(Ω0h),用Γ0h表示剖分在Γ0上的分划,Γ1h表示剖分在Γ1上的分划,Φh表示Sh(Ω0h)在Γ0上的迹空间[1,11]。(1)式的有限元近似:求uh∈Sh(Ω0h),满足a(uh,v)=l(v),∀v∈Sh(Ω0h)。
算法2 离散平方收敛不重叠Schwarz交替法[1]。算法步骤如下:
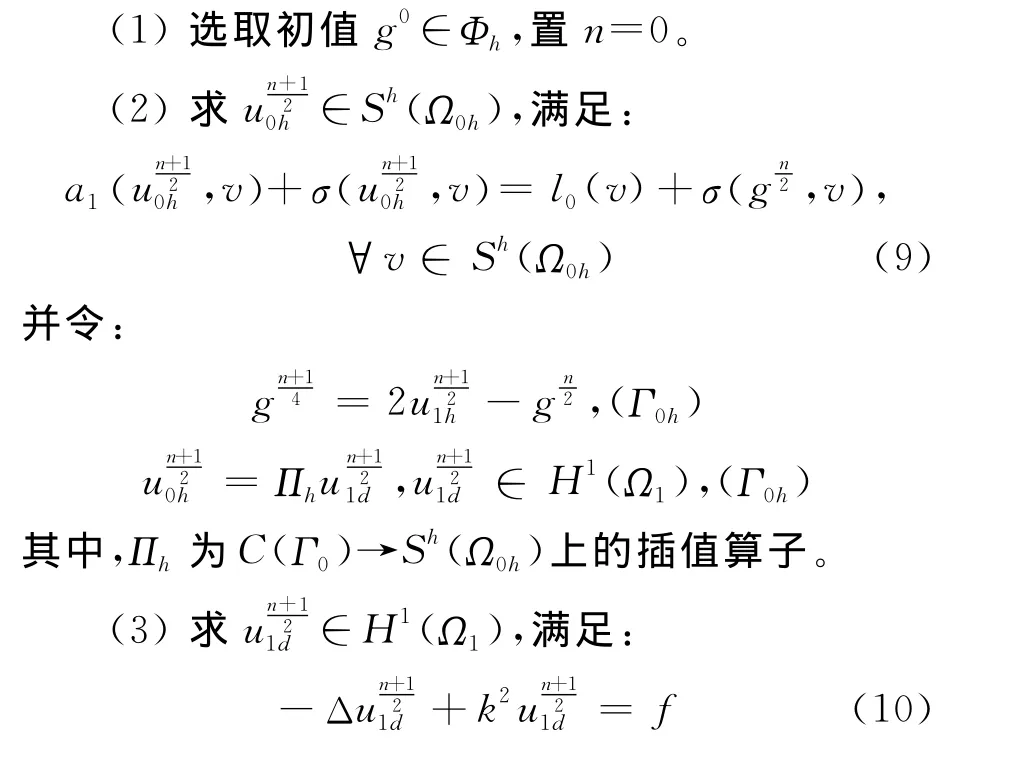
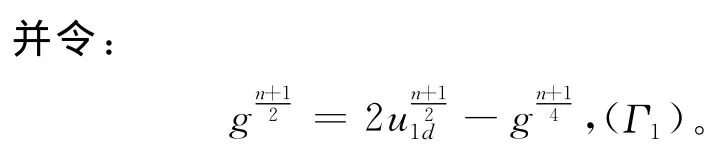
(4)转步骤(2)。
离散不重叠Schwarz算法中的(9)式在Sh(Ω0h)上利用有限元求解,(10)式因在无界区域上,故用自然边界归化方法。
2 数值算例
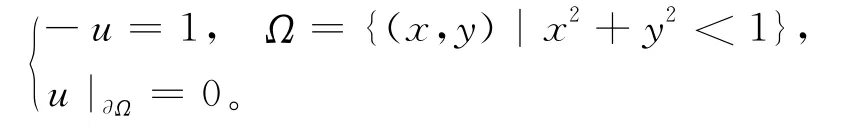
特殊地取f=1,考虑Dirichlet问题[11]:
为得到更好的算法收敛精度,既可以加密网格,也可以加密迭代函数,这里对函数进行二分,该迭代理论表明算法收敛误差相比于二分前以平方速度收敛。算例中部分节点数值见表1所列。数值算例前后u值和准确值与数值解的误差Matlab图像也表明相同结果,算法最终结果与真实值的误差对比如图1所示。
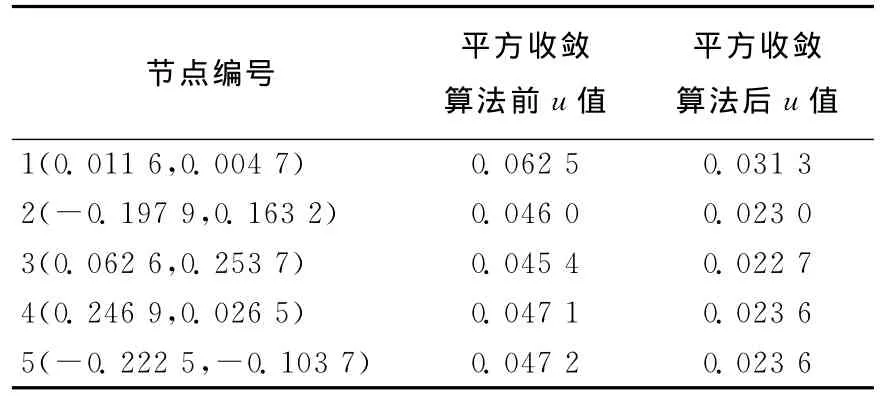
表1 算例中部分节点数值
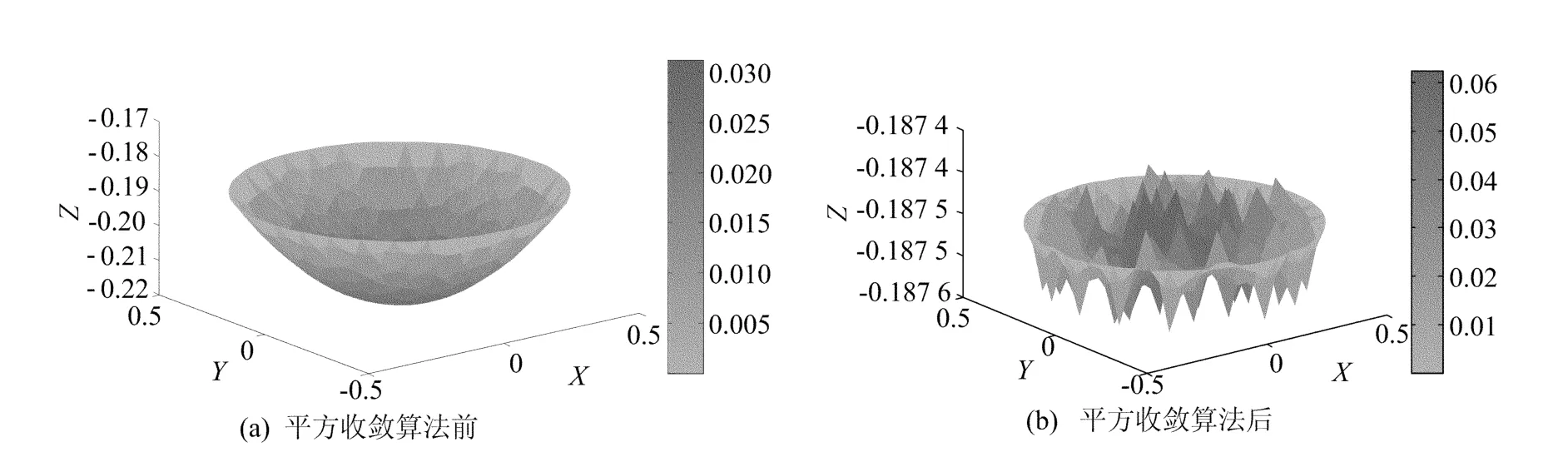
图1 算法最终结果与真实值的误差对比
3 结论
区域分解是基于自然边界归化原理处理无界区域问题的理论,其有相对完善的理论,能够解决无界区域上的PDE问题,且能够降低方程阶数,使计算量锐减。本文在此基础上加密迭代函数来获得加速收敛。
(1)平方收敛算法可以解决线性、非线性方程的数值解问题。逐步逼近的思想是将大区域问题逐步变为小区域问题。文中逐步逼近思想将网格加密与算法迭代函数二分换位,得到平方收敛的不重叠Schwarz交替法。将Schwarz交替法中的初始值与迭代函数的和取均值后代入替代,算法的收敛速度、误差估计性能提高。
(2)数值算例中部分节点数值和误差比较的Matlab图像表明平方收敛算法的优越性。
二分算法也可用在其他类型的偏微分方程的交替法上,文中仅以Poisson方程为例。
[1]刘红梅,王寿城.基于半平面上的不重叠Schwarz交替法[J].合 肥 工 业 大 学 学 报:自 然 科 学 版,2012,35(11):1582-1584.
[2]蒋美群.一个双调和方程的区域分裂法[J].苏州大学学报:自然科学版,1994,10(3):186-189.
[3]王寿城.不重叠型Schwarz交替法的加速收敛[J].应用数学学报,2004,27(2):237-245.
[4]陈战波,禹海青.函数配点法与不重叠Schwarz交替法求解椭圆方程[J].江汉大学学报:自然科学版,2008,36(3):14-16.
[5]董俊雨.无界区域各项异性椭圆型方程的基于自然边界归化的区域分解法[D].北京:北方工业大学,2008.
[6]王烈衡,许学军.有限元方法的数学基础[M].北京:科学出版社,2004:306-310.
[7]石钟慈,王 鸣.有限元方法[M].北京:科学出版社,2010:45-49.
[8]邬吉明.求解具有长条型内边界的外问题的一种重叠型区域分解算法[J].工程数学学报,2001,18(2):123-126.
[9]余德浩.自然边界积分方程及相关计算方法[J].燕山大学学报,2004,28(2):111-113.
[10]祝家麟,袁正强.边界元分析[M].北京:科学出版社,2009:45-49.
[11]陆君安.偏微分方程的 MATLAB解法[M].武汉:武汉大学出版社,2001:27-30.

