一类n维空间Riesz分数阶扩散方程的解析解

马亮亮， 刘冬兵

（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

分数阶微分方程可用于模拟生物、金融等领域及半导体研究中的许多现象［1］；文献［2－3］提出了分数阶的行方法，将分数阶微分方程转化为常微分方程系统；文献［4］考虑了有界区间上Riesz分数阶偏微分方程的数值问题；文献［5］给出了有界区间上分数阶空间扩散方程满足边界条件的数值解法；文献［6］考虑了一类Riesz－Caputo分数阶对流扩散方程在有限区间上的隐式和显式差分逼近；文献［7］讨论了一类二维空间Riesz分数阶扩散方程的解析解；文献［8］基于Riesz分数阶导数，对一类分数阶运动微分方程进行了研究。

本文将考虑n维情况下空间Riesz分数阶扩散方程的解析解问题。

1 定义及性质

定义1 在有界区间［0，L］上，Riesz分数阶导 数的定义［9］如下：

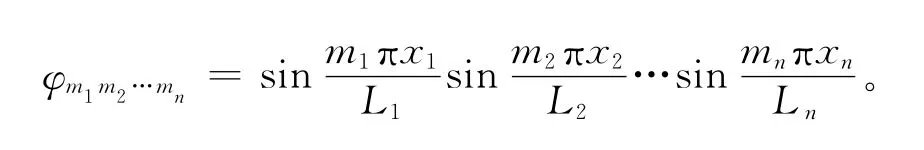
2 Riesz分数阶扩散方程的解析解

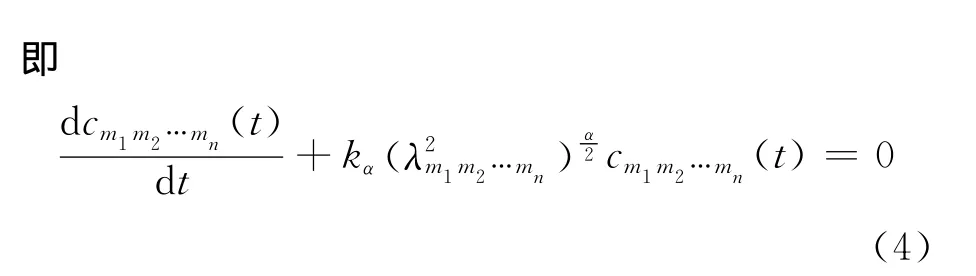
本文考虑齐次n维空间Riesz分数阶扩散方程为：根据常微分方程解的结构，可以推出（4）式的一般解为：

3 非齐次Riesz分数阶扩散方程的解析解

本文考虑非齐次n维空间Riesz分数阶扩散方程为：

根据叠加原理，非齐次n维空间Riesz分数阶扩散方程的初边值问题可转化为：

将f（x1，x2，…，xn，t）展成傅里叶级数的形式，即）

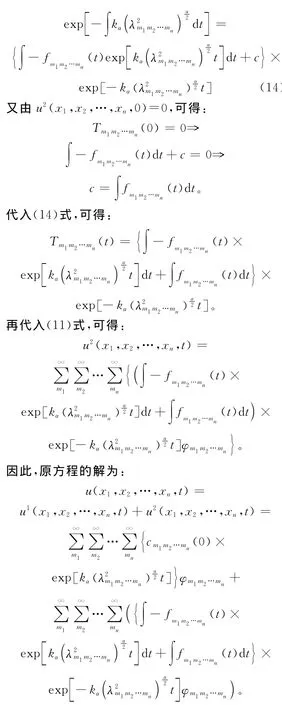
4 结束语

本文给出了n维空间Riesz分数阶导数与分数阶拉普拉斯算子的特征函数、特征值之间的关系，并利用谱表示法分别给出了齐次和非齐次情况下，一类n维空间Riesz分数阶扩散方程在有界区域内满足一定初边值条件的解析解。

［1］Liu F，Anh V，Turner I，et al.Numerical simulation for solute transport in fractal porous media［J］.ANZIAM J，2004，45（E）：461－473.

［2］Liu F，Anh V，Turner T.Numerical solution of the space fractional Fokker－Planck equation ［J］.J Comput Appl Math，2004，166：209－219.

［3］赵小文，张 海，蒋 威.分数阶时滞微分系统的解［J］.合肥工业大学学报：自然科学版，2009，32（9）：1439－1441.

［4］Yang Qianqian，Liu Fawang，Turner I.Numerical methods for fractional partial differential equations with Riesz space fractional derivatives［J］.Applied Mathematical Modeling，2010，34：200－218.

［5］Ilic M，Liu Fawang，Turner I，et al.Numerical approximation of a fractional in space diffusion equation［J］.Fract Caculus Appl Anal，1998，1（2）：167－191.

［6］Shen Shujun，Liu Fawang，Anh V V.Numerical approximations and solution techniques for the space－time Riesz－Caputo fractional advection－diffusion equation［J］.Numerical Algorithms，2011，56（3）：383－403.

［7］王学彬.一类二维空间Riesz分数阶扩散方程的解［J］.宁夏大学学报：自然科学版，2011，32（3）：222－225.

［8］张 毅，梅凤翔.基于Riesz分数阶导数的分数阶运动微分方程［J］.北京理工大学学报：自然科学版，2012，32（7）：766－770.

［9］Podlubny I.Fractional differential equations［M］.New York：Academic Press，1999：223－242.

［10］王学彬.二维、三维空间Riesz分数阶扩散方程的基本解［J］.山东大学学报：理学版，2011，46（8）：23－37.