服务补贴与具有共同零售商的Stackelberg博弈研究

王 磊， 刘圆圆， 孙 浩

（青岛大学 管理科学与工程学院，山东 青岛 266071）

0 引言

随着市场动态和竞争环境的变化，制造商日益重视使用非价格竞争策略，而不是仅仅依赖降低价格。服务即是一种关键的非价格因素，逐渐成为影响消费者购买决策的重要因素。它是制造商或零售商采取的能为顾客提供更大价值的行为，包括售前售后服务、产品广告、产品质量的提高、实时配送和用户体验等［1］。

事实上，零售商的服务对于提升顾客需求与增强顾客忠诚发挥着重要的作用［2－3］。

零售商为了实现自身利益的最大化，会通过提高商品的服务质量（如实物体验、个性化定制等）来提高商品的附加值，同时提高消费者福利；而制造商为使自己的产品能够在竞争中脱颖而出，占有更大的市场份额，只有通过向零售商提供一定的服务补贴等方法，才能得到零售商更大的服务支持，增加自身产品在服务方面的优势，从而提高利润［4］。

针对传统渠道，文献［5］研究了具有2个供应商和1个共同零售商的供应链，探讨了3种不同讨价还价力量的非合作博弈；文献［6］研究了由1个生产2种可替代产品的生产商和1个零售商的供应链中生产商决定服务由自己或者零售商提供的条件，以及零售商决定2种产品集中经营还是分散经营的条件；文献［7］对文献［5］的研究进行了拓展，增加服务因素，研究了价格、服务双重竞争下的渠道博弈问题；文献［8］研究了包括1个新产品生产商、再制造产品生产商和1个共同的零售商的供应链，识别出再制造努力、定价和服务决策的均衡特征，探讨了价格和服务不同组合竞争下的成员利润；文献［9］考虑生产商R＆D、零售商服务因素对渠道竞争的影响；文献［10］基于服务提供者的不同，分别研究了在Stackelberg和Nash博弈中供应商和零售商的决策。

针对双渠道的服务问题，文献［11］指出零售商服务质量的提高可以增加生产商的利润，更大范围的顾客服务敏感度将有利于双方；文献［12］在双渠道供应链中，使用两级优化技术和Stackelberg博弈研究了集中决策和分散决策中零售价格和服务的最优决策，分析了零售服务和顾客对零售渠道的忠诚度对生产商和零售商价格决策的影响；文献［13］建立了价格和服务敏感的双渠道竞争模型，研究了渠道服务竞争和网络渠道接受程度对双渠道供应链系统的影响；文献［14］研究了零售商提供服务的双渠道供应链，分析了零售商在不同的服务成本下提供服务对于供应商和零售商定价策略的影响。

本文研究了制造商作为Stackelberg主导者时的决策，考虑由2个制造商和1个共同零售商组成的供应链，前者通过后者分销产品，零售商为各自的产品提供服务。因此，制造商提供一定的服务补贴以激励零售商改善服务。

1 基本模型

本文假设所有的活动都发生在同一个时期内，在销售区域内只有1个零售商，也就是每个零售商之间的距离足够远，以至于这些零售商之间不存在竞争，这样可以把焦点集中在制造商之间的竞争上。假设影响消费者需求的因素只有零售价和服务水平，2个制造商采用相同的成本c。

假设提供服务成本的函数是关于服务水平递增的严格凸函数，也就是说零售商所投资的下一单位所获得的服务比所投资的上一单位获得的服务少，可以用二次形式表示［15］，即cs＝ηs2／2，其中η为服务成本系数，与服务提供者相关。

本文假设实际需求与零售价格和零售商的服务水平关系为：

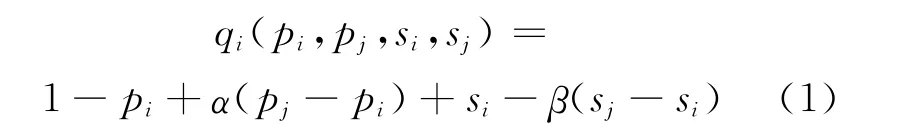
其中，i＝3－j（j＝0，1）；qi表示产品i的市场需求；1表示市场规模，也就是当零售价为0，且没有提供服务时的需求；pi和pj分别为产品i和产品j的零售价格；si和sj分别为零售商为产品i和j提供的服务水平；α为价格竞争强度系数，它表示一种产品增加（减少）一单位的价格或者另一种产品减少（增加）一单位的价格，都会带来α单位的减少（增加）；β为服务竞争强度系数，它表示一种产品增加（减少）一单位的服务或者另一种产品减少（增加）一单位的服务，都会带来α单位的增加（减少），α＞0，β＞0。

2 制造商不提供服务补贴的决策

当制造商不提供服务补贴时，制造商i的利润函数为：

零售商的利润函数为：

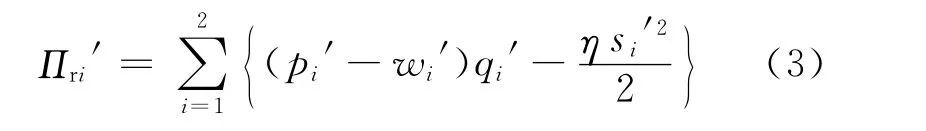
其中，pi′为制造商不提供服务补贴时产品i的零售价格；si′为制造商不提供服务补贴时零售商为产品i的服务水平；qi′为制造商不提供服务补贴时产品i的市场需求；wi′为制造商不提供服务补贴时产品i的批发价格；Πmi′为制造商i不提供服务补贴时制造商的利润；Πri′为制造商不提供服务补贴时零售商的利润。

在制造商主导的Stackelberg博弈下，零售商选择2种产品的零售价格p1′＊、p2′＊和服务水平s1′＊、s2′＊最大化自身的总利润，制造商利用零售商的反应函数决定最优的批发价格wi′＊。

2.1 零售商的决策

对零售商的利润函数求一阶导数得到零售商的反应函数，通过零售商的反应函数得出Hessian矩阵的值为（2η－1）［2η＋4ηα－（1＋2β）2］，当且仅当时有最大值。在满足Hessian矩阵大于0的条件下，对零售商利润函数求二阶导数，此时求得的零售价和服务水平相应的值为：

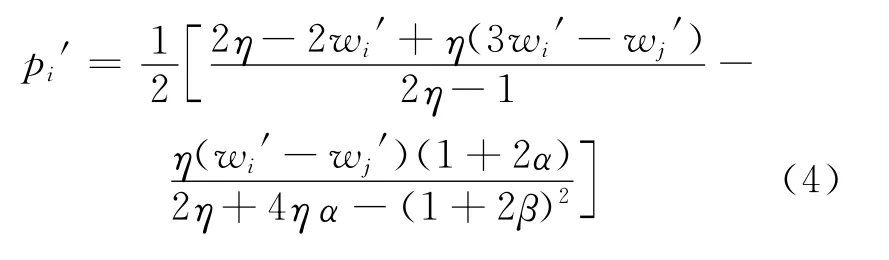
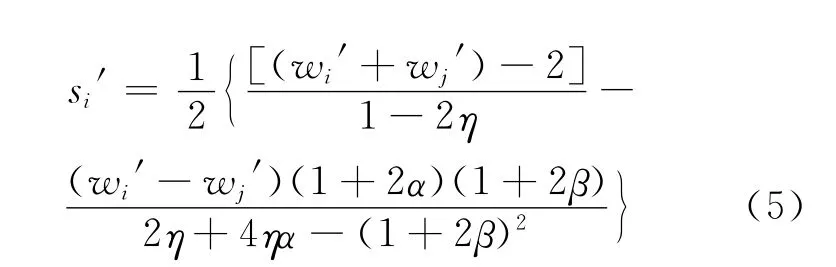
其中，i∈（1，2），i＝3－j。

2.2 制造商的决策

命题1 制造商i不提供服务补贴时的批发价格、零售价格、服务水平、零售商销售产品i的利润和制造商i的利润结果如下：

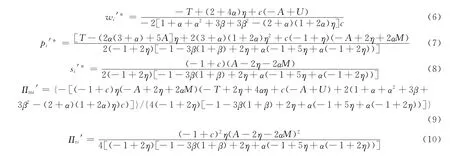
其中，A＝1＋2β（1＋β）；M＝－1＋3η＋α（－1＋2η）；T＝1＋4β（1＋β）；U＝－2α（1＋α）＋2（1＋α）（1＋2α）η。

分别令制造商i、j的利润函数的一阶导数等于0，然后联立得出制造商i利润函数取得最大值时的批发价格wi′和wj′，wi′和wj′进行联立得出最终的wi＊′和wj＊′，将wi′和wj′带入p1′、p2′和s1′、s2′，得 出p1＊′、p2＊′、s1＊′、s2＊′，最 后 即 可 求出制造商利润和零售商利润。

3 制造商提供服务补贴的决策

当制造商提供服务补贴时，制造商、零售商的利润函数分别为：

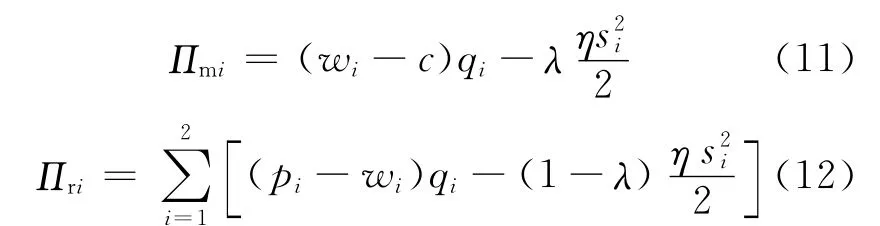
其中，λ为服务补贴系数，0≤λ≤1。

3.1 零售商的决策

在制造商提供服务补贴的Stackelberg博弈决策下，首先对零售商的利润函数求一阶导数得出其反应函数，其Hessian矩阵值为［2η（λ－1）＋1］［2η（λ－1）（1＋2α）＋（1＋2β）2］，当满足时有最大值。

在满足Hessian矩阵大于0的条件下，对零售商利润函数求二阶导数，此时求得的零售价和服务水平相应值为：

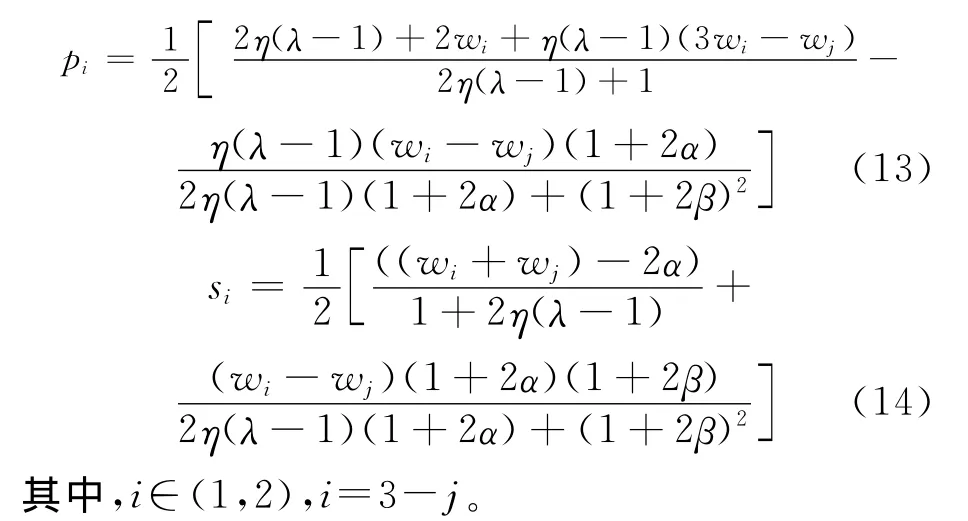
3.2 制造商的决策

命题2 制造商i提供服务补贴时的批发价格、零售价格、服务水平、零售商销售产品i的利润和制造商i的利润结果如下：

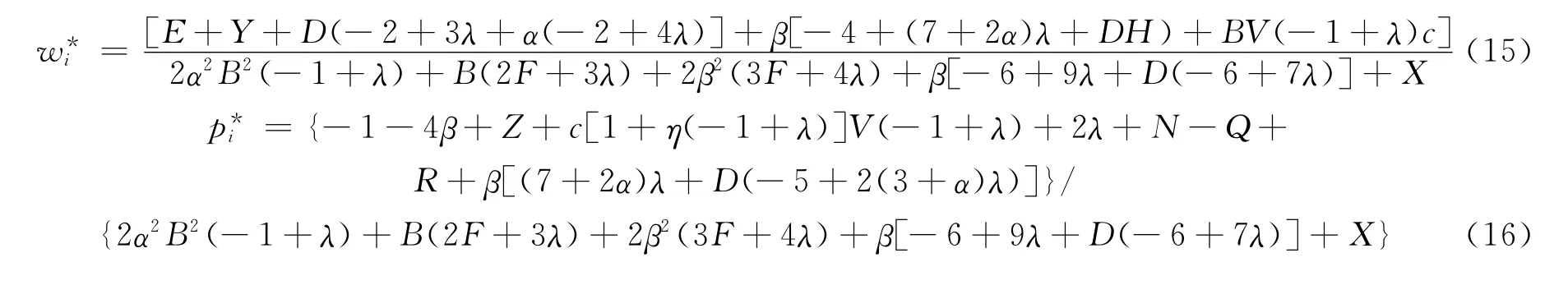
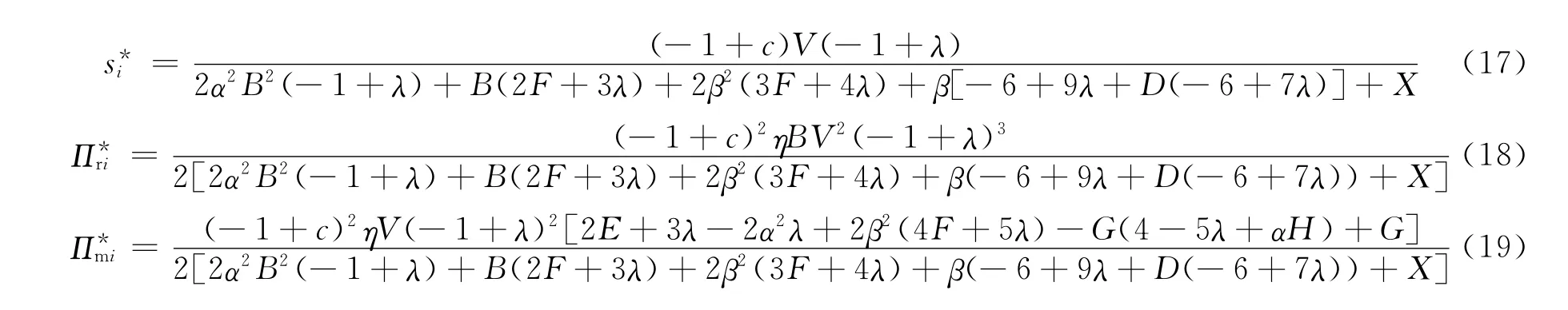
分别令制造商i、j的利润函数的一阶导数数等于0，然后联立得出制造商i利润函数取得最大值时的批发价格wi和wj，wi和wj联立得出最终的w＊i和w＊j，再将其带入p1、p2和s1、s2，得出2种产品最优的零售价格和最优的服务水平，最后可得到零售商和制造商的最大利润。

当制造商向零售商提供服务补贴时，供应链的整体利润增加，但有一方的利润增加，另一方的利润减少。因此，利润增加的一方必须向利润减少的一方提供一定的补偿，损失补偿的方法可以采用纳什讨价还价机制［16］，对增加的利润进行分配，这样就可以使利润减少的一方愿意提供或接受服务补贴。纳什讨价还价模型为：

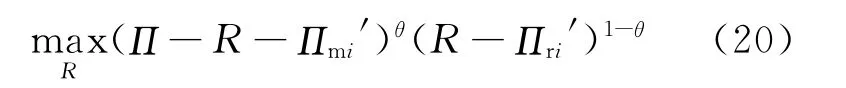
其中，Π为制造商提供服务补贴后制造商i和零售商销售产品i的整体利润；R为进行利润分配后零售商销售产品i的利润；Πmi′为制造商i不提供服务补贴时制造商i的利润；Πri′为制造商i不提供服务补贴时零售商销售产品i的利润；θ为制造商的议价能力；1－θ为零售商的议价能力。

由纳什讨价还价模型，可得最优解为：

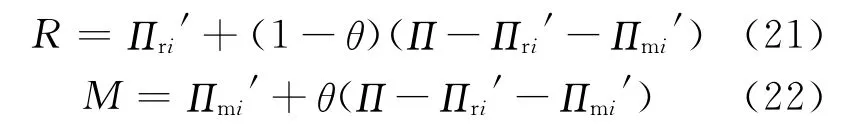
4 一体化情况的决策

在制造商和零售商一体化的情况下，其系统利润函数为：

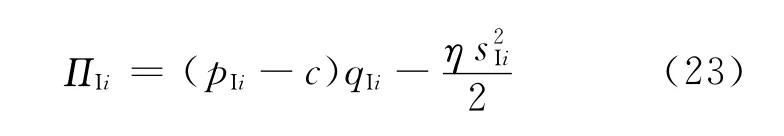
对利润函数求二阶导数求得Hessian矩阵的值为－（1＋β）2＋2（1＋α）η，当且仅当时，利润函数有最大值，此时求得的零售价和服务水平相应值为：

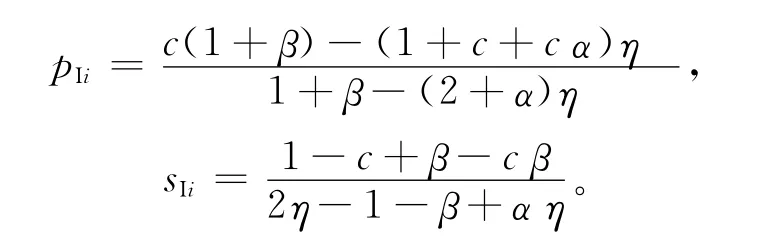
将零售价和服务水平带入利润函数，得出最大利润为：

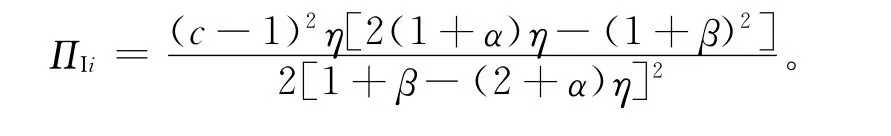
5 数值分析

5.1 服务补贴系数对均衡结果的影响

取α＝7，β＝1，c＝0.5，η＝5，θ＝0.6，分析各个变量与服务补贴系数λ之间的关系。由上述零售商利润最大化的条件，可知λ∈［0，0.88］。

（1）服务补贴系数λ对批发价格w、服务水平s、零售价格p和市场需求q的影响。w、s、p、q随λ的变化，如图1所示。

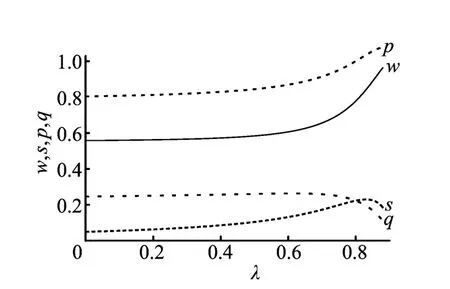
图1 w、s、p、q随λ的变化

从服务补贴系数λ对批发价格w的影响曲线可以看出，w在0≤λ＜0.88范围内，随着λ的增大而逐步增大，在λ＝0.88处取得最大值，wmax＝0.963 115，在λ＝0时取得最小值，wmin＝0.557 598。可知服务补贴系数的引入会使批发价格提高。

从服务补贴系数λ对零售商服务水平s的影响曲线可以看出，s在0≤λ＜0.829 92范围内，随着λ的增大而逐步增大，在0.829 92≤λ＜0.88时，随着λ的增大而减小，在λ＝0.829 92处取得最大值，smax＝0.229 398，在λ＝0时取得最小值，smin＝0.049 155 8。可知提供服务补贴时，零售商提供的服务水平永远高于不提供服务补贴时零售商提供的服务水平，所以制造商向零售商提供服务补贴，可以达到提高其产品服务水平的目的。

从服务补贴系数λ对零售价格p的影响曲线可以看出，p在0≤λ＜0.878 327范围内，随着λ的增大而逐步增大，在0.878 327≤λ＜0.88时，随着λ的增大而减小，在λ＝0.878 327处取得最大值，pmax＝1.073 88，在λ＝0时取得最小值为pmin＝0.810 183。由图1可以得出制造商提供服务补贴时的零售价永远高于不提供服务补贴时的零售价。

从服务补贴系数λ对制造商市场需求q的影响曲线可以看出，q在0≤λ＜0.611 998范围内，随着λ的增大而逐步增大，在0.611 998≤λ＜0.88时，随着λ的增大而减小，在λ＝0.611 998处取得最大值，qmax＝0.262 803，在λ＝0.88时取得最小值，qmin＝0.110 656 3，在λ＝0和λ＝0.756 439时，取qmin＝0.245 779。可以得出在0＜λ＜0.756 439时，产品的市场需求比不提供服务补贴时的市场需求有所增加。

如图2所示，一体化时的价格和服务都要低于分散时制造商提供服务补贴时产品的价格和服务，价格要相对明显，从消费者的角度来看，一体化可以为消费者提供更大的效用。

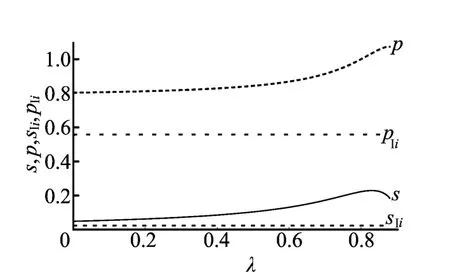
图2 s、p、sIi、pIi随λ的变化

（2）服务补贴系数λ对制造商i利润Πmi、零售商销售产品i的利润Πri、制造商i和零售商销售产品i的系统利润Πmi＋Πri的影响。如图3所示，从服务补贴系数λ对制造商利润Πmi的影响曲线可以看出，Πmi在0≤λ＜0.836 34范围内，随着λ的增大而逐步减小，在0.836 34≤λ＜0.88时，随着λ的增大而增大，在λ＝0.836 34处取得最小值，Πmimin＝－0.043 247 9，在λ＝0时取得最大值，Πmimax＝0.014 156 4。

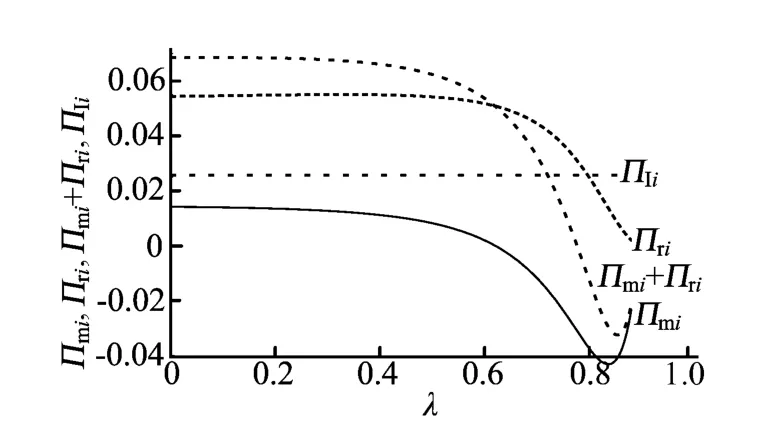
图3 Πmi、Πri、Πmi＋Πri随λ的变化

从服务补贴系数λ对零售商利润Πri水平的影响曲线可以看出，Πri在0≤λ＜0.327 032范围内，随着λ的增大而逐步增大，在0.327 032≤λ＜0.88时，随着λ的增大而减小，在λ＝0.327 032处取得最大值，Πrimax＝0.055 063 5，在λ＝0时，Πri＝0.054 366 5，在λ＝0.488 516时，零售商利润取值与λ＝0时取值相同，所以从零售商的角度考虑，在0＜λ＜0.488 516时，零售商的利润有所增加，此范围为零售商愿意接受制造商服务补贴的可行取值区间。

从服务补贴系数λ对制造商和零售商整体利润Πmi＋Πri的影响曲线可以看出，Πmi＋Πri在0≤λ＜0.078 305 9范围内，随着λ的增大而逐步增大，在0.078 305 9≤λ＜0.863 124时，随着λ的增大而减小，在0.863 124≤λ＜0.88时，随着λ的增大而增大，在λ＝0.078 305 9处取得最大值，（Πmi＋Πri）max＝0.068 572，在λ＝0.853 712时取得最小值，（Πmi＋Πri）min＝－0.032 586，在λ＝0时，Πmi＋Πri＝0.068 522 9，在λ＝0.144 634时的取值与λ＝0时取值相同。

可知在0＜λ＜0.144 634时，制造商和零售商的整体利润增加。此范围是供应链系统的可行取值区间，明显小于零售商可接受的区间范围。从最优服务补贴值来看，零售商最优的λ值明显大于对于系统利润最优的λ值。

当λ＞0.720 442时，制造商和零售商一体化时的利润大于提供服务补贴时制造商和零售商分散时的整体利润。

命题3 当服务补贴系数在低于一个定值的范围内逐渐增大时，批发价格、服务水平及零售价格增加，制造商的利润减少，而零售商利润和系统利润均增加。

在服务补贴系数λ＝0.078 305 9时，（Πmi＋Πri）max＝0.068 572，此时p＝0.806 251，s＝0.053 692 9，w＝0.558 809，Πmi＝0.013 987 4，Πri＝0.054 584 6，q＝0.247 442。当λ＝0时，即制造商不提供服务补贴时，p＝0.810 183，s＝0.049 155 8，w＝0.557 598，Πri＝0.054 366 5，Πmi＝0.014 156 4，Πmi＋Πri＝0.068 522 9，q＝0.245 779。由此可知，与不提供服务补贴相比，当λ＝0.078 305 9时，批发价格、服务水平、零售价格增加。制造商的利润减少，而零售商利润和系统利润均增加。

命题4 补贴系数λ取值小于某一值时，制造商利润虽然减少，但产品的销量增加。

在0≤λ＜0.611 998时，制造商的利润逐渐减少，但其产品销量却逐步增加，最大为qmax＝0.262 803，在λ＝0时，q＝0.245 779。由此可知，与不提供服务补贴相比，当0≤λ＜0.611 998时，零售商的利润增加，制造商的利润虽然减少，但是销量却逐步增加。从零售商利润角度考虑，零售商愿意接受来自制造商的服务补贴以分担其服务成本，提供更高水平的服务，增加销量，从而提高利润。从产品的市场份额角度考虑，制造商虽然利润减少，但制造商提供服务补贴可以增加其市场占有率，提高产品的知名度。

命题5 当服务补贴系数取值保证系统整体利润增加时，供应链中可以采用纳什讨价还价模型进行利润分配，使制造商和零售商的利润都得以改进。

供应链中制造商提供服务补贴使得制造商利润减少，制造商不愿向零售商提供服务补贴；在0＜λ＜0.488 516时，零售商的利润有所增加，零售商愿意接受来自于制造商的服务补贴，但制造商不愿提供服务补贴；在0＜λ＜0.144 634时，制造商和零售商的整体利润增加，虽然零售商愿意接受服务补贴，但制造商不愿提供。因此，可以采用纳什讨价还价模型对利润进行分配，由最优解可知当其整体利润最大时，进行分配后的制造商和零售商的利润最大。当λ＝0.078 305 9时，制造商和零售商的整体利润最大为0.068 572，Πri′＝0.054 366 5，Πmi′＝0.014 156 4，此时可以得出R＝0.054 395 96，M＝0.014 176 04。可知R＞Πri′，M＞Πmi′，此时制造商愿意提供服务补贴，零售商愿意接受服务补贴。

5.2 价格竞争强度对均衡结果的影响

取β＝1，c＝0.5，η＝5，θ＝0.6，λ＝0.5时，分析各个变量与价格竞争强度系数α之间的关系。由上述零售商利润最大化的条件可知α∈［0.4，＋∞］。

（1）价格竞争强度系数α对批发价格w、服务水平s、零售价格p和市场需求q的影响。如图4所示，从α对批发价格w的影响曲线可以看出，w在0.4≤α＜0.832 159范围内，随着α的增大而逐步增大，在α＞0.832 159时，w随着α的增加逐步减小，在α＝0.832 159处取得最大值，wmax＝0.675 646，在α＝0.4时，w＝0.647 059，在α＝2.25时的取值与α＝0.4时取值相同。

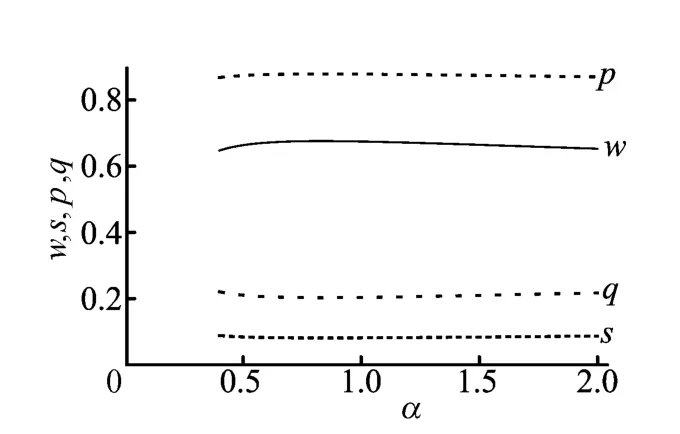
图4 w、s、p、q随α的变化

从α对零售商服务水平s的影响曲线可以看出，s在0.4≤α＜0.832 159范围内，随着α的增大而逐步减小，在α＞0.832 159时，随着α的增大而增大，在α＝0.832 159处取得最小值，smin＝0.081 088 5。

从α对零售价格p的影响曲线可以看出，p在0.4≤α＜0.832 159范围内，随着α的增大而逐步增大，在α＞0.832 159时，随着α的增大而减小，在α＝0.832 159处取得最大值，pmax＝0.878 367。从α对制造商市场需求q的影响曲线可以看出，q在0.4≤α＜0.832 159范围内，随着α的增大而减小，在α＞0.832 159时，随着α的增大而增加，在α＝0.832 159时取得最小值，qmin＝0.202 721。

（2）价格竞争强度系数α对制造商i利润Πmi、零售商利润Πri、制造商i和零售商销售产品i的系统利润Πmi＋Πri的影响，如图5所示。

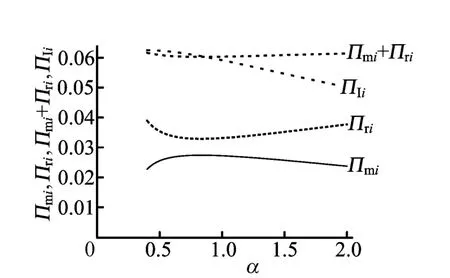
图5 Πmi、Πri、Πmi＋Πri随α的变化

从α对制造商利润Πmi的影响曲线可以看出，Πmi在0.4≤α＜0.832 159范围内，随着α的增大而增加，在α＞0.832 159时，随着α的增大而减小，在α＝0.832 159处取得最大值，Πmimax＝0.027 388。

从α对零售商利润Πri水平的影响曲线可以看出，Πri在0.4≤α＜0.832 159范围内，随着α的增大而减小，在α＞0.832 159时，随着α的增大而增加，在α＝0.832 159处取得最小值，Πrimin＝0.032 876 7。

从α对制造商和零售商整体利润Πmi＋Πri的影响曲线可以看出，Πmi＋Πri在 0.4≤α＜0.832 159范围内，随着α的增大而逐步减小，α＞0.832 159时，随着α的增大而增加，在α＝0.832 159时取得最小值，即

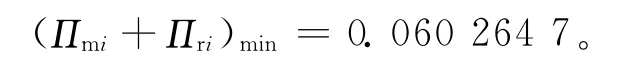
当α＞0.865 982时，制造商和零售商一体化时的利润小于提供服务补贴时制造商和零售商分散时的整体利润。

命题6 当服务补贴系数确定时，存在一个价格竞争强度系数，使批发价、零售价和制造商的利润随着价格竞争强度系数的增大而增大，而服务水平、市场需求、零售商利润和系统利润随着价格竞争强度系数的增大而减小。

当λ＝0.5时，批发价、零售价和制造商的利润在α＝0.832 159处取得最大值，服务水平、市场需求、零售商利润和系统利润在α＝0.832 159处取得最小值。

5.3 服务竞争强度对均衡结果的影响

取α＝7，c＝0.5，η＝5，θ＝0.6，λ＝0.5时，分析各个变量与服务竞争强度系数β之间的关系。由上述零售商利润最大化的条件可知

（1）服务竞争强度系数β对批发价格w、服务水平s、零售价格p和市场需求q的影响，如图6所示。

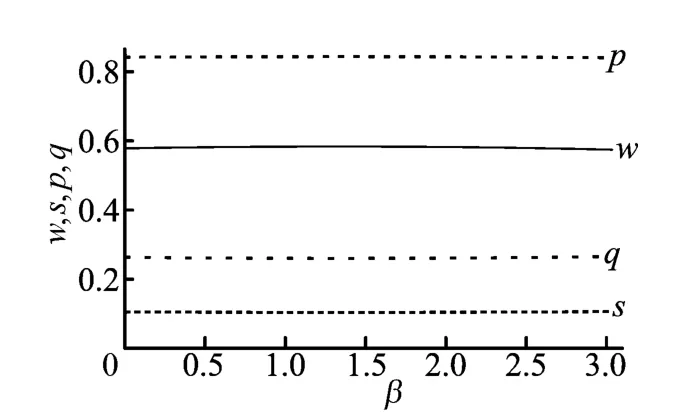
图6 w、s、p、q随β的变化

（2）服务竞争强度系数β对制造商i利润Πmi、零售商利润Πri、制造商i和零售商销售产品i的系统利润Πmi＋Πri的影响，如图7所示。

命题7 当服务补贴系数确定时，存在一个服务竞争强度系数，使批发价、市场需求和制造商利润随着服务竞争强度的增大而增大，而服务水平、零售价、零售商利润和系统利润随着服务竞争强度的增大而减小。

当λ＝0.5时，服务水平、市场需求和制造商利润在β＝1.330 37处取得最大值，批发价、零售价、零售商利润和系统利润在β＝1.33 037处取得最小值。

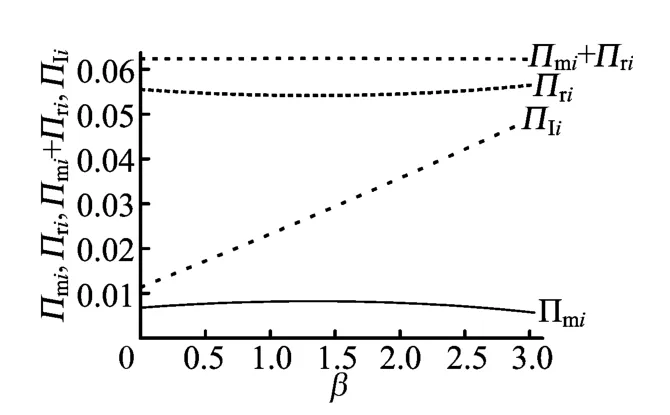
图7 Πmi、Πri、Πmi＋Πri随β的变化

5.4 服务成本系数对均衡结果的影响

取α＝7，β＝1，c＝0.5，θ＝0.6，λ＝0.5时，分析各个变量与服务成本系数η之间的关系。由上述批发价、零售价、服务水平不小于0和零售商利润最大化的条件，可知η∈［0.975，＋∞］。

（1）服务成本系数η对批发价格w、服务水平s、零售价格p和市场需求q的影响，如图8所示。

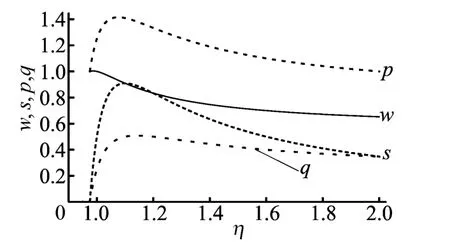
图8 w、s、p、q随η的变化

（2）服务成本系数η对制造商利润Πmi、零售商利润Πri、制造商i和零售商销售产品i的系统利润Πmi＋Πri的影响，如图9所示。

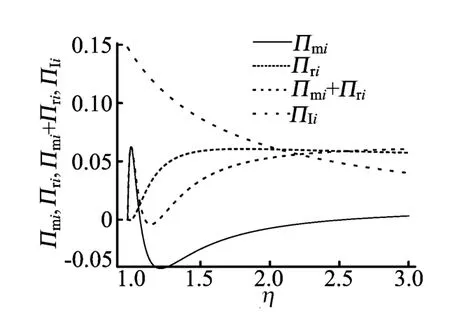
图9 Πmi、Πri、Πmi＋Πri随η的变化

命题8 批发价格、服务水平、零售价、市场需求和零售商利润随着服务成本系数的增大先增大后减小，制造商利润和系统利润随着服务成本系数的增大先增大后减小再增大。

6 结束语

本文研究了由2个制造商和1个共同零售商组成的供应链，2个制造商将具有可替代性的2种产品通过1个共同的零售商进行销售，零售商为其产品提供服务，制造商为零售商提供服务补贴。由于研究比较复杂，本文选择在带入数值后对结果进行分析。

向零售商提供服务补贴，虽然能够提高零售商针对自己产品所提供的服务水平，增加其产品的市场占有率和零售商的利润，但并不能增加制造商的利润，反而会使其利润减少。如果在制造商向零售商提供服务补贴的供应链中采用纳什讨价还价机制，不仅可以使产品服务和销量保持在不采用纳什讨价还价机制的制造商向零售商提供服务补贴时供应链的水平，还可以使制造商和零售商的利润都增加，此时制造商愿意提供服务补贴，零售商愿意接受服务补贴。因此，制造商向零售商提供服务补贴有利于供应链的发展，具有一定的研究意义。

［1］Goffin K.Customer support：a cross－industry study of distribution channels and strategies［J］.International Journal of Physical Distribution ＆ Logistics Management，1999，29（6）：374－397.

［2］顾平平，王 晓.从汽车产业发展政策谈我国汽车售后服务［J］.上海汽车，2004（9）：15－17.

［3］胡启林.沈阳机床4S店已达18家［N］.中国工业报，2012－09－10（4）.

［4］刀 影.美三大运营商押注上网本 将向零售商提供补贴［EB／OL］.（2009－07－23）.http：／／it.sohu.com／20090723／n265438938.shtml.

［5］Choi S C.Price competition in a channel structure with a common retailer［J］.Marketing Science，1991，10（4）：271－296.

［6］Iyer G.Coordinating channels under price and nonprice competition［J］.Marketing Science，1998，17（4）：338－355.

［6］Xia Yusen，Gilbert S M.Strategic interactions between channel structure and demand enhancing services［J］.European Journal of Operational Research，2007，181：252－265.

［7］Lu J C，Tsao Y C，Charoensiriwath C.Competition under manufacturer service and retail price［J］.Economic Modelling，2011（28）：1256－1264.

［8］Wu Chenghan.Price and service competition between new and remanufactured products in a two－echelon supply chain［J］.International Journal of Production Economics，2012（140）：496－507.

［9］梁 樑，王 磊，汤卫君.R＆D、服务与双边垄断的供应链［J］.系统工程，2005，23（5）：33－41.

［10］许明辉，于 刚，张汉勤.具备提供服务的供应链博弈分析［J］.管理科学学报，2006，9（2）：18－26.

［11］Dumrongsiri A，Fan Ming，Jain A，et al.A supply chain model with direct and retail channels［J］.European Journal of Operational Research，2008（187）：691－718.

［12］Dan Bin，Xu Guangye，Liu Can.Pricing policies in a dualchannel supply chain with retail services［J］.International Journal of Production Economics，2012（139）：312－320.

［13］陈远高，刘 南.具有服务差异的双渠道供应链竞争策略［J］.计算机集成制造系统，2010，16（11）：2485－2489.

［14］孔庆山，邢 伟，石晓梅.具有服务策略的双渠道供应链定价问题研究［J］.商业研究，2012，418：114－118.

［15］Tsay A A，Agrawal N.Channel dynamics under price and service competition［J］.Manufacturing ＆ Service Operations Management，2000，2（4）：372－391.

［16］Baron O，Berman O，Wu D.Supply chain and its implication to coordination of supply chains in an industry［R］.Toronto：the University of Toronto，2008.