地铁车站隧道监控量测数据的回归分析
王兴宏,万文,王超林,段艳平
(湖南科技大学土木工程学院,湖南湘潭 411201)
随着我国进入城市地铁隧道建设的黄金时期,人们越来越重视隧道建设新型技术的使用,新奥法的施工就是其中之一[1-4]。锚杆、喷射混凝土和施工监测是新奥法的三大要素,监控测量则是新奥法中极其重要组成部分之一,通过监控量测来发现围岩和支护结构的承载-变形-时间特性,许多学者对此进行了分析研究[5-8]。本文采用Origin专业绘图软件对监控量测数据进行处理,通过对隧道监控量测数据的回归分析,可以科学、客观的分析被监测的对象,了解当前围岩支护的状况,同时可以有效的预测隧道拱顶沉降和周边收敛的最终值。
1 工程概况
曹家湾站位于北碚区蔡家岗镇灯塔村南侧约0.8 km处,中环路从其北侧约0.4 km处通过,车站呈南北向设置于规划纵二路及其支路的交汇处,东北、西北、西南侧为规划的居住用地,东南侧为商业用地。
曹家湾站为地下二层岛式车站。车站总长185.00 m,车站起点里程:YDK41+479.967,车站终点里程YDK41+664.967,车站分界终点里程YDK41+664.967,有效站台中心里程为 YDK41+548.917,车站有效站台中心里程处轨面高程为323.464 m。车站主体为暗挖法施工,两端区间隧道采用复合式TBM施工。
2 回归模型
2.1 拱顶下沉回归模型
2.1.1 S.H.KIM 、N.Y.KIM 模型
国外比国内对岩石隧道的研究多,1981年国外学者Komi用统计的方法得出了在新奥法隧道施工过程中距离隧道掌子面1D(D为隧道的近似直径)范围内拱顶沉降值与最终沉降值的比值为一个定值。之后 S.H.KIM、N.Y.KIM 等人在零距离量测原理的基础上得到了拱顶下沉值的预测方法,拱顶下沉位移值随着掌子面跟进的监控量测数据可以通过采用指数函数对其进行回归分析,其回归模型为:

式中,S为隧道拱顶中心点的下沉值;A、B、X0为常数。
2.1.2 Panet和 Guadin硬质岩体隧道变形分析模型
1979 年,国外学者Panet和 Guadin采用收敛限制法分析了隧道拱顶沉降(周边位移收敛)与离隧道掌子面距离之间的关系,并通过拟合得到了一个硬质岩体隧道的变形经验公式,其表达式为:

式中,δ(x)为隧道的变形量,即隧道的拱顶下沉值或周边位移收敛值;δ∞x为因隧道掌子面的推进而产生的隧道拱顶沉降值或周边位移收敛的极限值;X为隧道掌子面所影响的区域距离,与岩体的塑性半径R0有关,可用以下表达式计算:

式中,a是常数,取值为 0.84。
2.1.3 Sulem 模型
软岩隧道变形模型不同于硬质岩体隧道变形模型,假如将隧道监控量测断面布置在掌子面附近位置,所得围岩的变形量是由软岩的流变效应和距掌子面推进距离影响产生的变形量共同组成的。当监控量测断面距离与隧道掌子面较远时,隧道掌子面将失去支撑量测断面附近的岩体的能力,此时隧道围岩的变形量受围岩流变效应控制。因此,在1987年Sulem提出软质围岩隧道变形量由掌子面推进所致围岩变形量和时间效应所致围岩变形量之和,即隧道开挖时空效应的变形理论,其表达式为:

式中:X为隧道掌子面往前推进的所影响的区域距离;T为隧道围岩的流变特性参数;δ∞r为不考虑隧道围岩发生流变时,因隧道掌子面的推进而产生的瞬时沉降的极值;m、n为常数。
2.2 隧道周边位移收敛的回归模型
在隧道的施工中的监控量测数据受环境、人为操作因素的影响,数据的波动很大,存在很大的误差,因而需要对监测数据进行回归建模,才能探寻到周边位移收敛的发展规律,以便为施工提供指导,目前主要采用指数、对数和双曲线三种曲线函数进行线性回归计算。三种函数均可转换为线性方程进行回归分析。

式中u为隧道围岩变形量;t为时间;a、b为回归常数。
3 监测数据分析与应用
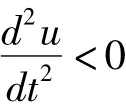
下面以重庆曹家湾车站某断面的监控量测数据为例,进行回归分析。拱顶下沉位移-时间的关系,通过拱顶下沉 S.H.KIM 、N.Y.KIM 模型进行分析,其表达式为 S=A[1-exp(-B(XX0))],根据表达式拟合的曲线见图1,从图1可以看出,S.H.KIM 、N.Y.KIM 模型能较为准确的拟合实际监测数据。由于变形加速度,说明断面变形随时间的增加越来越小,对应的沉降速度也在不断的减少,这与实际测量计算所得到的结果较为吻合(见图1),通过拟合曲线发现:开挖初期拱顶下沉位移值变化较大,说明开挖对围岩的扰动较大,随后拱顶下沉位移值变化趋于稳定,说明围岩充分发挥了自承能力,拟合曲线能够准确的预测拱顶下沉变化趋势,通过拟合曲线可以得到拱顶下沉的最终沉降为11 mm。
通过Origin绘图软件,将监控量测周边收敛绘图并通过周边收敛模型u=alg(1+t)对曲线进行非线性拟合,可以得函数中的相关系数。表1为拟合函数的相关系数。

表1 拟合函数的相关系数Tab.1 The correlation coefficient of fitting function

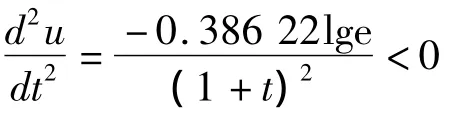
5 结论
使用Origin软件对监测数据进行对数函数拟合,可以预测隧道拱顶沉降的最终值为11 mm,隧道的周边收敛为8 mm;采用围岩稳定性判断标准对监测数据进行回归分析,可以得到隧道围岩是处于安全状态,因此通过对量测数据的分析处理,可以掌握围岩稳定性的变化规律,以便及时施作二衬。
[1]朱汉华,杨建辉,尚岳全.隧道新奥法原理与发展[J].隧道建设,2008(1):11-14.
[2]林勇.对公路隧道新奥法施工监控技术的展望[J].公路交通技术,2004(4):84-87.
[3]孙文,岳大昌.隧道工程新奥法原理、施工与存在问题浅析[J].公路交通技术,2012(2):98-100.
[4]宋旭亮,徐 矫.新奥法在超深竖井施工中的应用[J].水利与建筑工程学报,2013(1):148-150.
[5]秦之富,唐 健.高速公路隧道监控量测及应用[J].公路交通技术,2006(2):99-104.
[6]王胜涛,梁小勇,周亦涛.隧道监控量测的数据回归分析探讨[J].隧道建设,2009(6):629-632.
[7]李秀芳,柯玉军,徐长峰,等.公路隧道监控量测数据的回归分析及其运用[J].公路交通科技:应用技术版,2013(1):178-182.
[8]李品钰.隧道现场施工监控量测数据分析中回归模型的选择与优化[D].长沙:长沙理工大学,2012.

