振荡流底层拟序结构运动理论模式

陈汉宝，徐海珏,，白玉川,

振荡流底层拟序结构运动理论模式

陈汉宝1，徐海珏1,2，白玉川1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072)

湍流拟序结构是一种可检测的有序运动，在壁面湍流结构中往往表现出复杂的三维结构．针对对称振荡流(纯振荡流)，建立了描述对称振荡流湍流拟序结构的理论模式，并对其特性进行了研究．探讨了振荡流拟序结构能够保持的雷诺数范围、拟序扰动波数范围以及所能激发不稳定拟序波的波数频率范围，分析了振荡流激发的二维扰动波与三维扰动波的相互关系以及拟序波的对称性特征、拟序扰动流速、雷诺应力、附加涡量的时空分布等．结果表明，对称性振荡流拟序结构不仅与通常研究的雷诺数等因素有关，而且与振荡频率有很大的关系．

振荡流；拟序结构；稳定性特征

切变湍流的拟序结构是近年湍流研究中的重大发现，它表明湍流并非完全不规则运动，在表面上看来不规则的运动中具有可检测的有序运动，这种运动在切变湍流脉动发生和发展中起着重要的作用．

边界层湍流较自由切变湍流更为复杂，由于受到床面壁限制，湍流结构往往是三维的．早期湍流边界层理论认为床面附近的流动是层流，并称之为层流底层；自20世纪50年代以来，大量湍流研究表明所谓的层流底层并非层流，它是触发湍流的重要区域．1967年Kline等[1]用氢泡显示了平板边界层近壁区的拟序结构，该研究工作被认为是认识剪切湍流中准周期与准确定性拟序结构存在的经典研究工作；之后经过20年的研究，人们才对单向平板边界层流拟序结构有了比较清晰的认识[2]．

对于振荡流拟序结构的研究，主要是结合波浪掀沙及振荡流掀沙机理进行研究，Black[3]分别就对称振荡流(纯振荡流)和非对称振荡流(波流)近底流区(离床面高度为5～46,mm范围内)在其一个运动周期内的掀沙状况进行了室内实验和现场观测研究，发现在其一个运动周期内，存在3个掀沙峰值，最大的峰值出现在振荡流水质点由正向转反向的瞬间，此时质点轨道速度和底部切应力都很小，且它们均处于减速阶段，这样按照常规计算波浪掀沙的方法，就很难加以描述．通过深入的实验研究表明，浅水对称振荡流(纯振荡流)和非对称振荡流(波浪)的掀沙过程及掀沙含量滞后于底部切应力和轨道速度的原因主要是由于底边界层紊动结构而并非泥沙的惯性所致，即决定于振荡流底层中的拟序结构，其演化及其猝发喷射大涡喷射对床面形态的发展、床面泥沙的掀动上扬起着决定性的作用．

振荡流底层拟序结构在自然界起着重要的作用，吸引了无数学者对其进行研究，其一是针对振荡流本身紊动结构，其二是将紊动结构引入振荡流掀沙过程.对于前者，Hino等[4]、Sleath[5]和Jensen等[6]曾分别就光滑床面、粗糙床面及高雷诺数等情况，对振荡流本身湍流特性、底层拟序结构发展过程进行实验研究，发现在振荡流加速阶段，湍流首先由底层的剪切不稳定性失稳而激发产生，但此时尚被主流抑制而不能发展，只有到振荡流减速阶段的开始，湍流才逐步强烈地增长并以拟序猝发的运动形式所表现出来，若此时床面若有足够的泥沙供给，则将产生强大的掀沙上扬通量．Hagatun等[7]、Horikawa等[8]、Dick等[9]和Savioli等[10]的掀沙实验和现场实测结果从另一方面也的确相继证实了这一点．

对于平板底层拟序结构的研究，目前既有实验也有理论和数值方面的研究，已取得了较大的进展[11]；对于振荡流底层稳定性研究目前也是研究的热点[12-14]；而对于振荡流底层拟序结构的研究，目前刚刚起步，迄今为止理论方面鲜见报道，笔者就是希望在该方面做初步探讨．

1 理论模式

1.1 基本方程

以平底床面为例，取振荡流底边界层外最大流速umax、振荡流底层厚度δ=2ν/ω和振荡流基本频率ω，分别作为特征流速、特征长度和特征时间，无量纲化Navier-Stokes方程为其他方向的表达式类似．

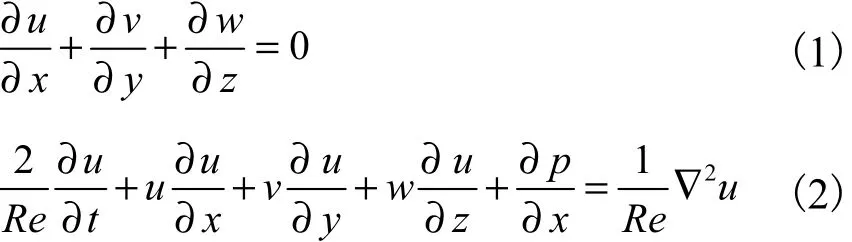
1.2 拟序相平均和拟序分解

1)拟序事件

在时空(x，t)中任一点的{xc，tc}触发一次拟序运动称为一拟序事件．

2)拟序相平均

拟序事件的平均称为拟序平均〈〉u，如拟序速度场的相平均为

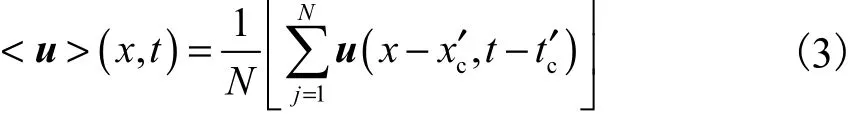
3)拟序分解

将湍流流动分解为拟序相平均和脉动之和，称作拟序分解.

4)拟序扰动

拟序相平均和全系综平均(或雷诺平均)之差定义为拟序扰动.

结合式(4)和式(5)可以看出，在引入拟序事件、拟序相平均和拟序扰动后，在拟序分解的情况下，速度压力可分解为

可以看出全系综平均分解的脉动项实质上是拟序扰动和拟序脉动之和.

1.3 拟序扰动方程

将式(6)代入式(1)和式(2)中，做拟序平均和全系综平均，然后用前者减去后者可以得到拟序扰动方程．

振荡流实验[8-10]表明，湍流大尺度拟序结构与小尺度结构同时存在，但小尺度结构对大尺度结构的发展所起的作用不大，因此，可不考虑湍流小尺度结构的影响，有其他方向的表达式可做类似展开．

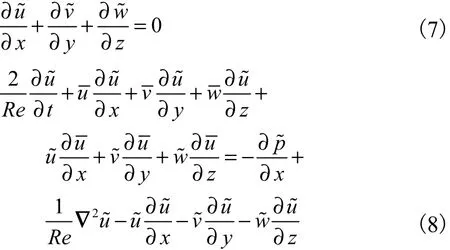
1.4 基本流速度分布

振荡流底层接近平行流，故基本流方程可化简为

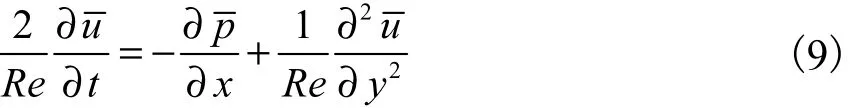
而边界层外区为势流运动，不存在剪切力，其运动方程为

式中：pw为边界层外压强；wu为边界层外水质点的水平速度，由Stokes理论知其无量纲的形式为

式中C.C代表共轭复数．跟据边界层理论，p=pw，用式(9)减去式(10)，有

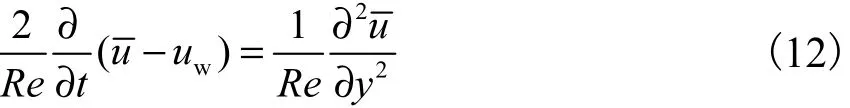
利用分离变量法，并考虑到wu的表达式，则

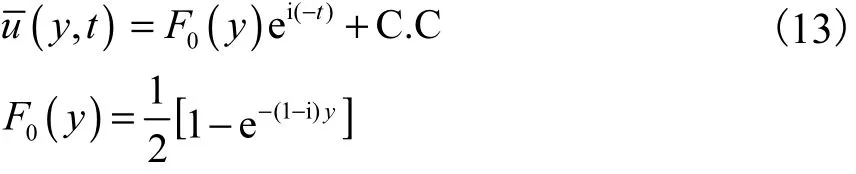
绘出的图形如图1所示．其中，横坐标为用边界层外最大流速umax无量纲化的振荡流速，而纵坐标为用边界层厚度δ无量纲化的垂向深度坐标．

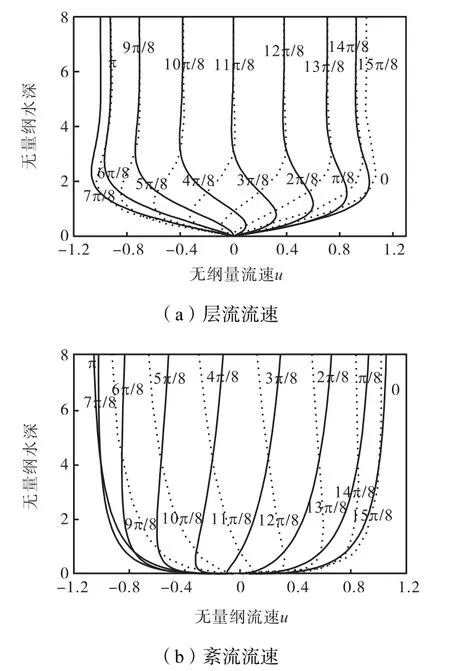
图1 振荡流流速分布Fig.1 Velocity distribution of oscillatory flow

以上是层流情况下的流速分布，但目前讨论的是底层湍流拟序的运动，因此，应将其修整到湍流情况．根据Nielsen[15]的研究结果，F0(y)修整为

1.5 拟序运动的理论分析

壁湍流中拟序运动具有强烈的三维效应，如纵向条带和纵向涡，目前比较公认的推测是，某种扰动通过非线性作用，在近壁面处形成三维扰动，三维扰动在近壁面处发展起来，导致流向速度剖面具有拐点，这种局部不稳定剖面进一步失稳、崩溃破裂，发生猝发现象，完成一个拟序运动过程．在振荡流中也存在类似的现象，实验研究表明，这种拟序大尺度结构实际上是一种不稳定波，而小尺度结构对大尺度结构的演化作用不大，可以用流动稳定性的理论来研究其运动特性．

1.5.1 拟序扰动摄动展开

将式(14)代入式(7)和式(8)，得

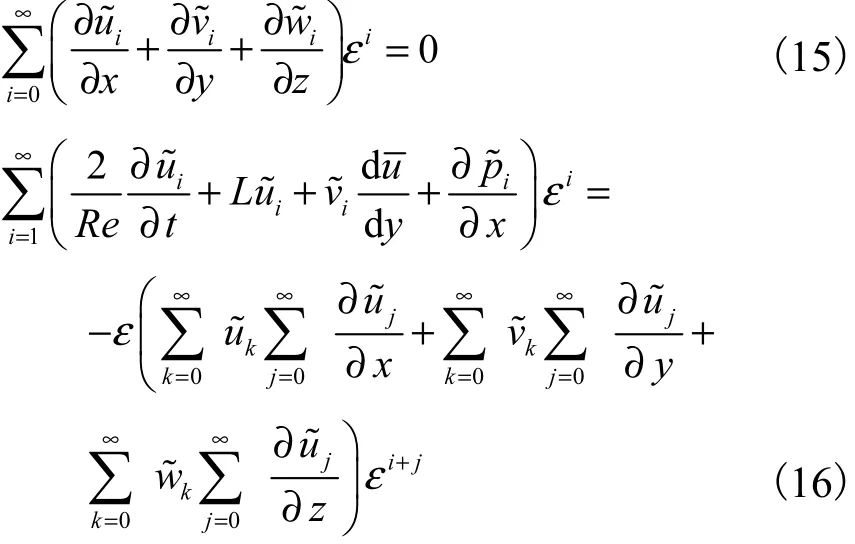
1.5.2 拟序扰动运动线性分析

略去上述方程中的高阶量，只保留线性部分，即得0ε的相关方程为

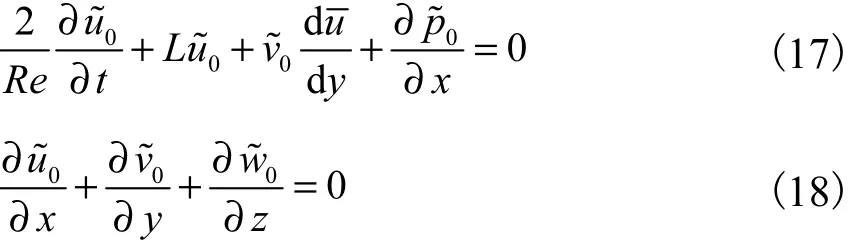
实验研究表明，这种拟序大尺度结构实际上是一种不稳定波；同时实验研究也发现，振荡流底层的拟序结构，既有二维的成分，同时也具有三维的成分，因此，本文对其线性部分亦用二维扰动和三维扰动加以构造与模拟．

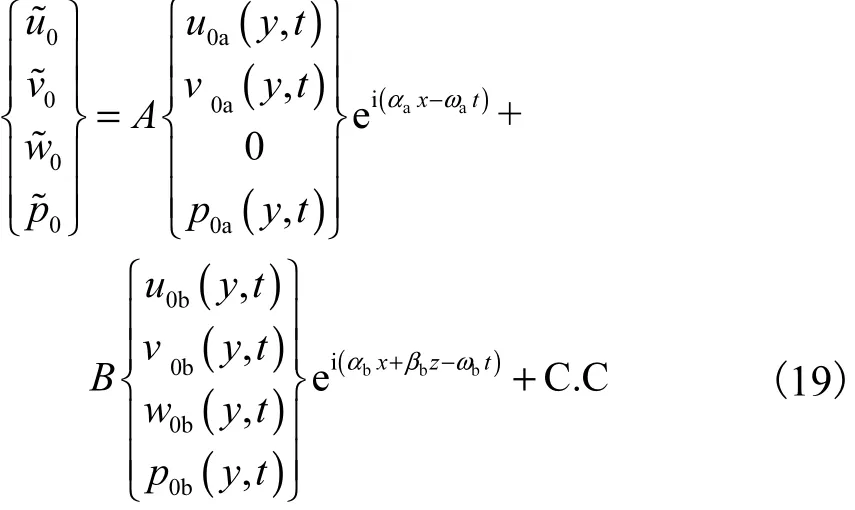
式中：下标“0a”表示二维拟序；下标“0b”表示三维拟序．将式(19)代入式(17)和式(18)中，先考虑ei(αbx+βbz-ωbt)项，消去u0b(y,t)、w0b(y,t)和p0b(y,t)后得三维Orr-Sommerfeld方程为

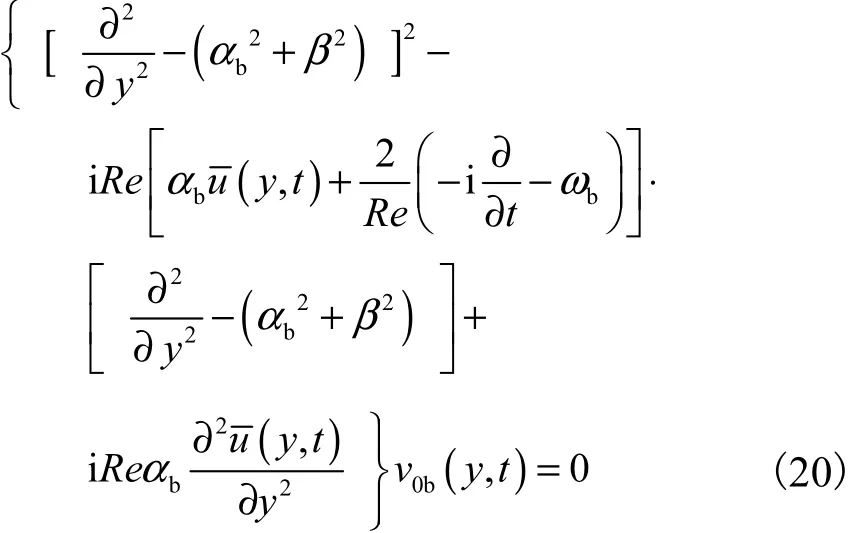
边界条件整理为

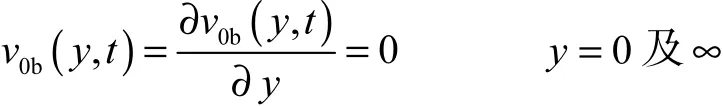
由于u(y,t)为周期函数，利用Floquet理论，v0b(y,t)可展为级数形式，即

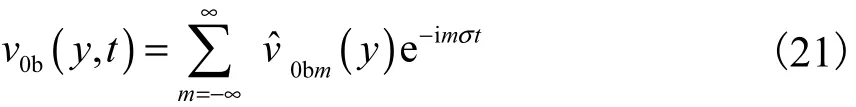
式(21)中1σ=，结合式(13)，式(19)可重新写为

将式(13)、式(21)代入式(20)中，相应于e-imσt项 (m取不同的正整数)，所有特征函数所满足的方程为

当0y=及∞时，有

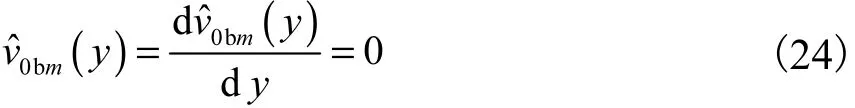
式(23)代表了振荡流边界层流动稳定性特征的Orr-Sommerfeld方程，依此研究拟序大尺度结构这种不稳定波的变化情况．类似常规处理二次稳定性的方法[4]，对于式(22)，在m=1处截断，即m〉1，v0bm(y)=0．令m=-1,0,1，共3个方程，结合边界条件(24)，共同构成了特征问题，求解可得出所有的vˆ0bm(y)．当β=0时，方程即可代表二维情况，同理可求出所有的vˆ0am(y)．

2 分析及计算结果

2.1 对称性分析

边界层内流速u(y,t)=F0(y)ei(-t)+C.C在一个时间周期[0,2π]内，有方向相反幅值相同的2个过程的运动，即

这2个过程共同组成了振荡流的整个周期性运动过程，这样就出现了成对的对称性振荡流的特征值，即分别有正向传播扰动波和逆向传播的扰动波.

本文首先采用谱配置方法将方程离散，然后采用具有移位的QR方法进行全部特征值的筛选计算，最后采用Muller方法进行详细计算．表1中列出了用QR方法计算得到的最具代表性的3个特征值(ωb)的结果(Re=522，αb=0.15，β=0，σ=1.0)来说明问题．

表1 特征值比较分析Tab.1 Comparison of eigenvalues

2.2 类Squire变换及稳定性特征

考虑到Squire变换关系，引入类似变换，其关系为

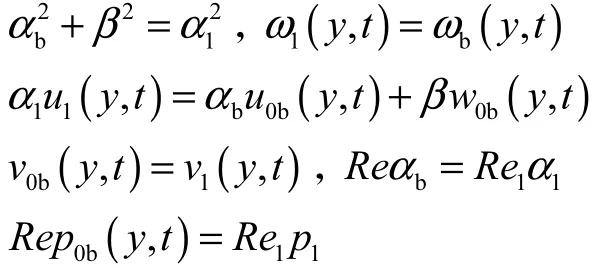
则式(20)可变为

其形式与考虑二维情况下的方程形式是一致的，所以，仍然可以证明在二维流向波数与三维流向波数、展向波数的关系满足Squire变换的情况下，由Reαb=Re1α1可知，Re≤Re1，即在坐标变换关系α2b+β2=α21下，二维拟序涡首先出现．

本文的特征值问题归结为求满足F(αb,β,ωb, Re,σ)=0的αb、β、ωb、Re和σ的关系问题，其中无量纲化量纲σ=1，所以可变变量有4个. 围绕这4个变量的变化，给出特征值的变化情况．

图2和图3给出的是特征频率在波数-雷诺数平面上的分布情况．图2为特征值虚部等值线图，其中实线代表稳定的中性曲线．图2中的3等值线表现出了一定的规律，在波数较小的范围内，中性线在大雷诺数方向，而且3等值线表现出了较散的趋势．随着波数的增长，中性线向小雷诺数方向移动，并在αb≈0.215处，中性线到达雷诺数最小处，此即为临界雷诺数，再向上中性线又向大雷诺数的方向发展．在波数增大的过程中，3等值线也表现出了从散到集中的过程．图3为特征值实部等值线图，在中性曲线分布相当的范围内特征值实部表现出了相对均匀的分布情况，随着波数和雷诺数的增加，特征值实部也逐渐增加．

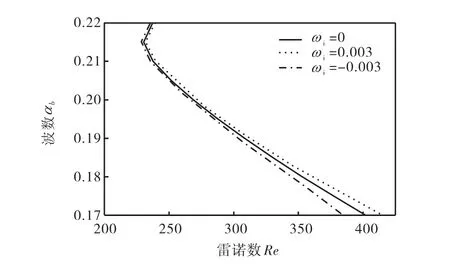
图2 特征值虚部等值线Fig.2 Contour of imaginary part of eigenvalue

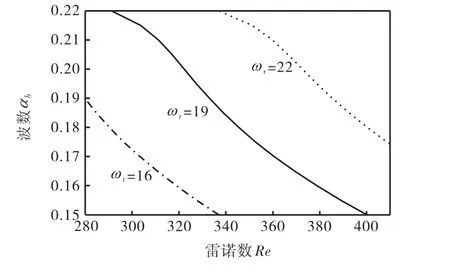
图3 特征值实部等值线Fig.3 Contour of real part of eigenvalue

为了证明Squire变换，将Squire变换关系和计算结果进行了对比，其结果吻合．图4给出了不同展向波数下中性曲线等值线图．可以看出，对于对称性振荡流的流动稳定性问题，同样可以进行Squire变换，将三维问题转换成二维问题进行分析；而且也有相当于平面Poiseuille稳定性的结论，即二维失稳首先出现，然后才会由于共振机理向三维扰动转变．

图4 不同展向波数下中性曲线等值线Fig.4Contour of neutral curve under different spanwise wave numbers

2.3 扰动流速分布

图5～图8给出了计算得到的扰动流速及扰动压强分布规律，其中纵坐标y代表用边界层厚度δ无量纲化的垂向深度．从图5～图7中可以看出，3方向上的扰动流速u、v、w都显示出相似的规律．由于近底给定的是无滑移边界条件，所以扰动流速在底部都是从零起步，在一定高度范围内出现了幅度较小、波长较短的振荡，随着距离底部距离的加大，幅值和波长逐渐变大，从而在离地面高度大约为10δ ～30δ的范围内达到峰值，能量在此集中较多．向上的发展趋缓，幅值逐渐趋于零．整个趋势显示出在振荡流不稳定发生初期，扰动能量在底部聚集、慢慢向水面扩散的发展过程．

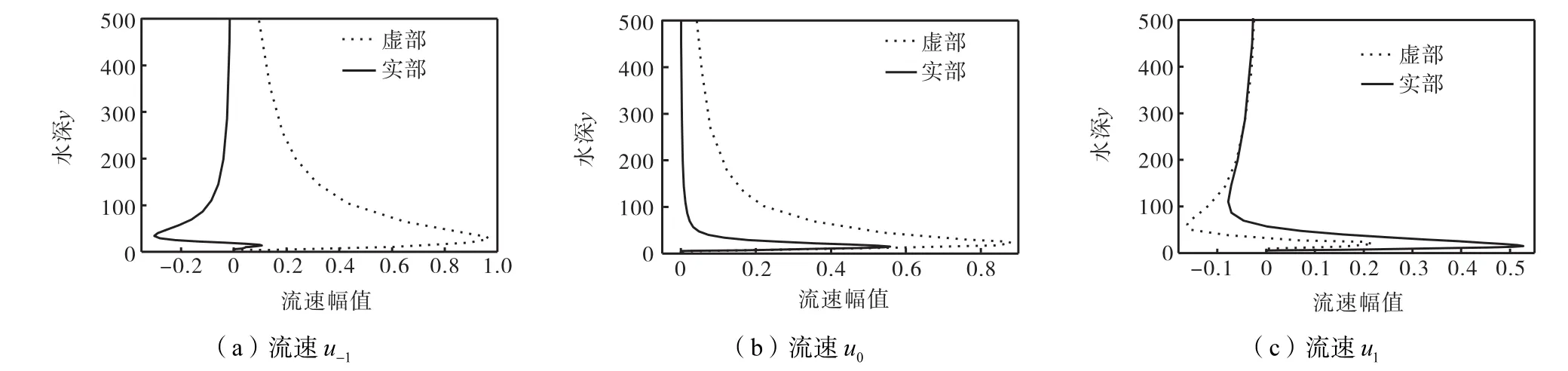
图5 扰动流速u沿水深的变化Fig.5 Variation of disturbance velocity u along water depth

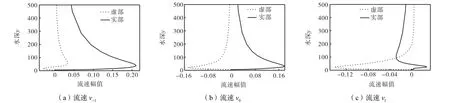
图6 扰动流速v沿水深的变化Fig.6 Variation of disturbance velocity v along water depth

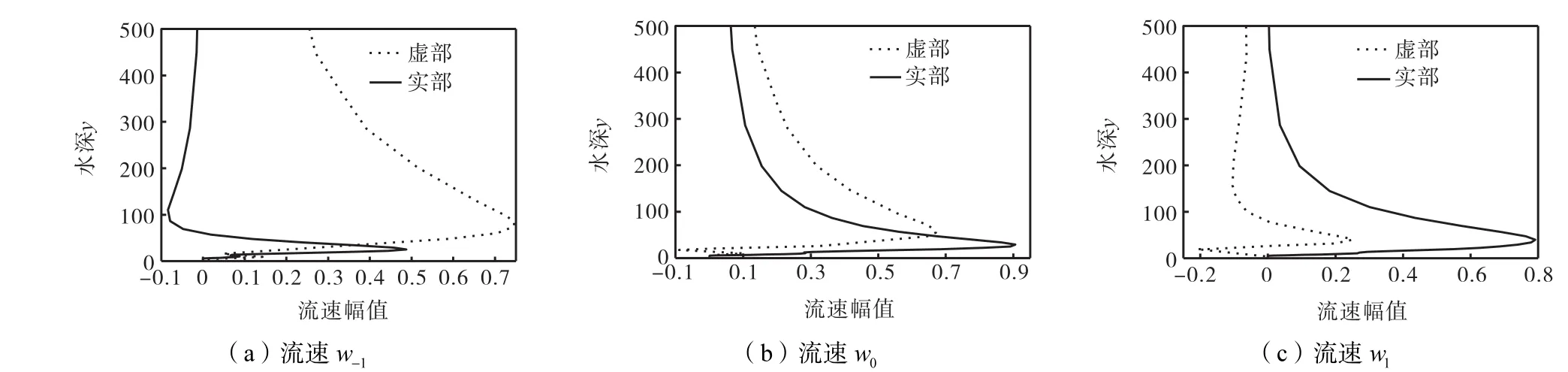
图7 扰动流速w沿水深的变化Fig.7 Variation of disturbance velocity w along water depth

图8 扰动压强沿水深的变化Fig.8 Variation of disturbance pressure along water depth

2.4 雷诺应力分布

图9给出了雷诺应力的分布情况．从图9可以看出，各方向上的雷诺应力在底部为零，在距离底部不高的地方出现了高频振荡，振荡的波长和幅值随高度的增加而增加并在高度为30δ 处达到其峰值；并且由于受到边界的影响，流向上的雷诺应力(uu)和展向上的雷诺应力(ww)明显比纵向上的雷诺应力(vv)大．水平方向上雷诺应力(uu和ww)的这种变化将对床面产生巨大影响，暴露在沙质床面上的非均匀泥沙颗粒受振荡频率和各种不同扰动频率的影响，在床面上做悬移、推移或跃移运动，成为沙波形态出现的前提条件．而纵向的雷诺应力也不容忽视，它的产生可能对泥沙颗粒的悬扬有重要影响．

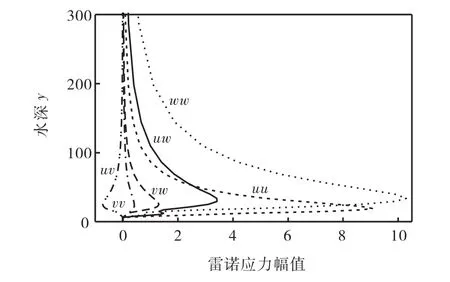
图9 雷诺应力沿水深的变化Fig.9 Variation of Reynolds stress along water depth

图10 和图11给出了雷诺应力在不同位置上的对比．从图中可以看出，雷诺应力在不同位置上的变化较小，而且整体变化趋势相同，在同一位置(高度为8δ )处出现明显的幅值变化，在几乎同一位置(高度为30δ )处达到其峰值，有的可在一定位置(高度10,δ )附近观察到明显的幅值反复，如图10(c)和图11所示，这就是高频短波振荡的明显表现．

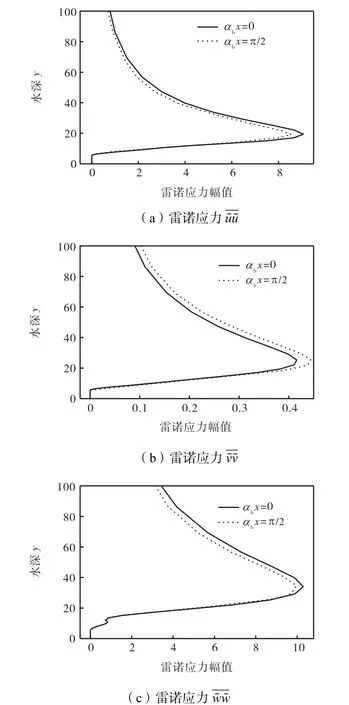
图10 正向雷诺应力在不同位置上的对比Fig.10 Normal Reynolds stress at different positions

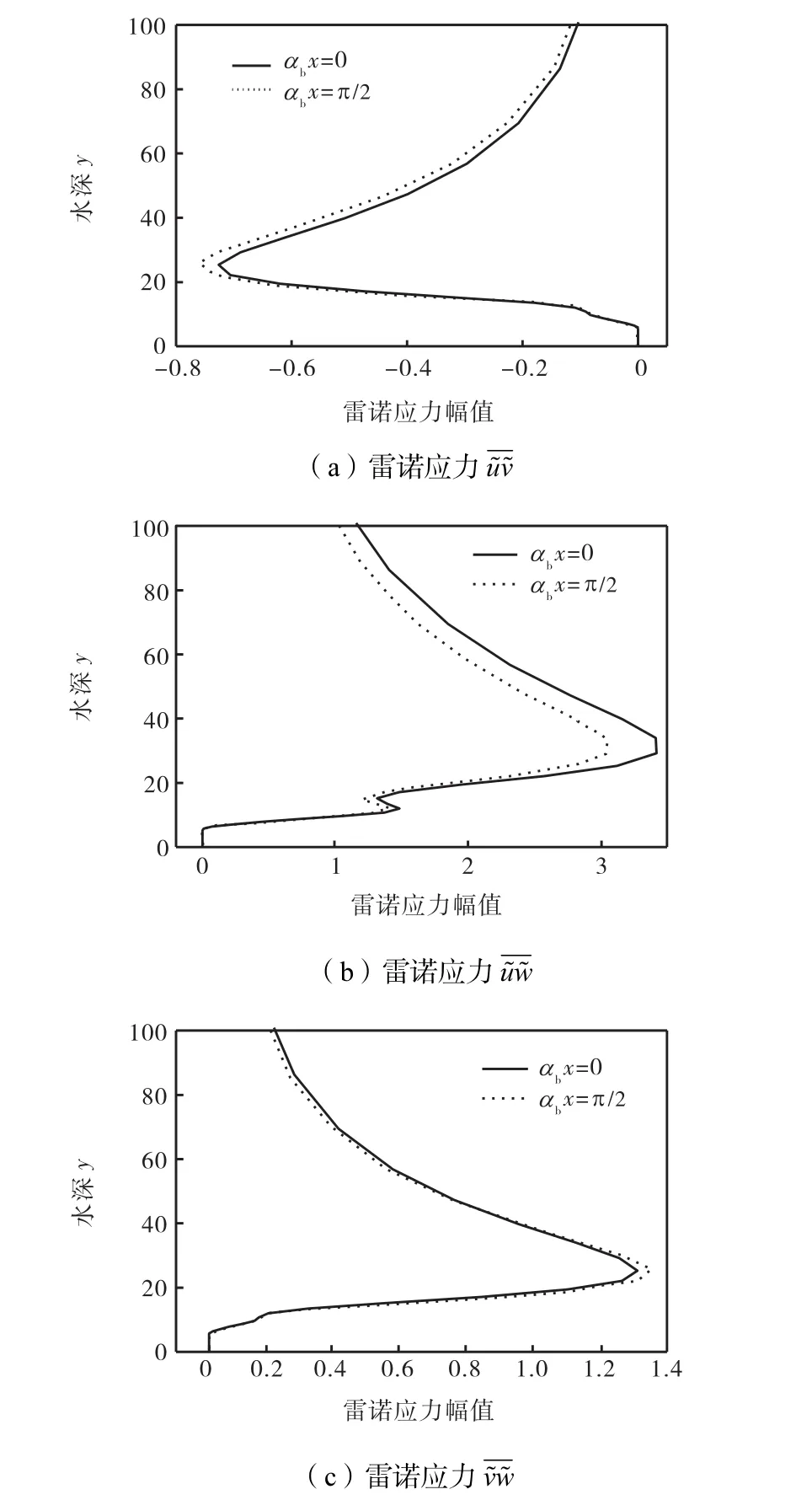
图11 切向雷诺应力在不同位置上的对比Fig.11 Tangential Reynolds stress at different positions

2.5 附加涡量分布

振荡流流速转向时往往能使水挟带更多泥沙[16-19]，本文的研究结果显示，振荡流拟序扰动产生和发展所带来的附加涡量在转向时达到最大，能够显著影响到泥沙的挟带量，从而影响到床面的形成过程．从图12可以看出，涡量的幅值也有从底部向水面上逐渐增加达到峰值然后逐渐减少的过程．对比3个方向的涡量，发现其在流向(x方向)上幅值最大，在展向(z方向)上幅值最小，在这2个水平方向上具有相似的结构特点，而在纵向上结构复杂，幅值也较小．对比图10、图11和图5～图8，发现附加涡量的衰减速度比扰动流速快，并与雷诺应力具有相当的数量级．

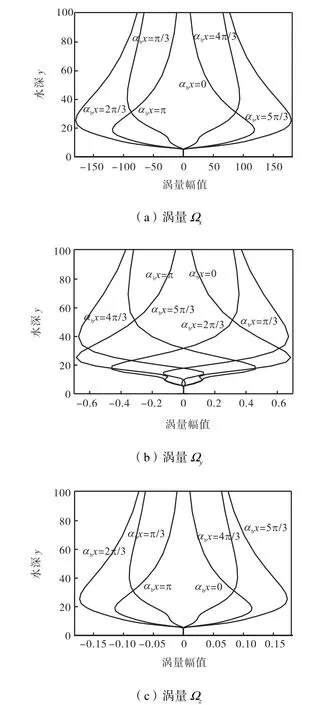
图12 涡量在不同位置上的对比Fig.12 Comparison of vorticity at different positions

3 结 论

本文应用Floquet理论，讨论了振荡流底层拟序结构特征．通过理论分析和数值计算，得到如下结论.

(1) 对称振荡流由于在边界层内流速在一个时间周期内，可以分成2个方向相反幅值相同的运动过程．这样就造成了振荡流失稳有成对的特征值，它们具有相反的实部和相同的虚部，其实部表明了它们相反的传播方向，而虚部则表明了它们共同的稳定性特征．

(2) 从图2中的3条等值线可以看出，在波数较小的范围内，中性曲线向大雷诺数方向弯曲，三维等值线较散．而随着波数的增长，中性曲线慢慢达到雷诺数最小处，然后又继续向大雷诺数方向发展，在这个过程中，等值线一直比较紧凑．

(3) 与平面Poiseuille流相同，振荡流的三维Orr-Sommerfeld方程也可以经过类似于Squire变换变成二维形式的方程．同时也可以证明在二维波数与三维流向波数、展向波数满足Squire变换的条件下，二维拟序涡首先出现．

(4) 扰动流速在底部都为零，随着水深的慢慢增加，在一定高度范围内都出现了幅度小而波长短的振荡，这种振荡幅值和波长随着距离底部的距离加大而加大，在距离底部约10δ ～30δ 的范围内达到峰值，并在继续加大距离后逐渐趋于零．

(5) 雷诺应力的分布情况基本与扰动流速类似，也在距离底部不高的地方出现了振荡，这种振荡在高度为30δ 的范围内达到峰值．从各雷诺应力分量的对比可以看出，由于受到壁面边界的影响，流向和展向上的雷诺应力明显比纵向上的雷诺应力大．

(6) 涡量的幅值也有从底部向水面逐渐增加达到峰值后逐渐减少的过程，逐渐趋于零的速度类似于雷诺应力，而快于扰动流速．对比3个方向上的涡量，发现其流向上的幅值最大，而在展向上最小，纵向上结构复杂．

［1］ Kline S J，Reynolds W C，Schraub F A，et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics，1967，30：741-773.

［2］ 是勋刚. 湍流 [M]. 天津：天津大学出版社，1994.

Shi Xungang. Turbulence[M]. Tianjin：Tianjin University Press，1994(in Chinese).

［3］ Black K. Suspended sediment load during an asymmetric wave cycle over a plane bed[J]. Coastal Engineering，1994，23(1/2)：95-114.

［4］ Hino M，Kashiwayanagi M，Nakayama A，et al. Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow[J]. Journal of Fluid Mechanics，1983，131：363-400.

［5］ Sleath J F A. Turbulent oscillatory flow over rough beds[J]. Journal of Fluid Mechanics，1987，182：369-409.

［6］ Jensen B L，Sumer B M，Fredsφe J，et al. Turbulent oscillatory boundary layer at high Reynolds numbers[J]. Journal of Fluid Mechanics，1989，206：265-297.

［7］ Hagatun H，Eidsvik K. Oscillating turbulent boundary layer with suspended sediments[J]. Journal of Geophysical Research，1986，91(c11)：13045-13055.

［8］ Horikawa W，Watanabe A. Turbulence and sediment concentration due to wave[J]. Coastal Engineering in Japan，1970，13：15-24.

［9］ Dick J E，Sleath J F A. Velocities and concentrations in oscillatory flow over beds of sediment[J]. Journal of Fluid Mechanics，1991，233：165-196.

［10］ Savioli J，Justesen P. Sediment in oscillatory flows over a plane bed[J]. Journal of Hydraulic Research，1997，35(2)：177-189.

［11］ Nezu I，Nakagawa H. Turbulent structure in unsteady depth varying open channel flow[J]. Journal of Hydraulic Engineering，ASCE，1997，123(9)：752-763.

［12］ Luo Jisheng，Wu Xuesong. On the linear instability of a finite Stokes layer：Instantaneous versus Floquet modes[J]. Physics of Fluid，2010，22(054106)：1-13.

［13］ Blennerhassett P J，Bassom A P. The linear stability of high-frequency oscillatory flow in a channel[J]. Journal of Fluid Mechanics，2006，556：1-25.

［14］ Wu X，Luo J S. Influence of small imperfection on the stability of plane Poiseuille flow and the limitation of Squire’s theorem[J]. Physics of Fluids，2006，18(044104)：1-13.

［15］ Nielsen P. On the structure of oscillatory boundary layers[J]. Coastal Engineering，1985，9(3)：261-276.

［16］ 白玉川，徐海珏. 平板和翼型壁面上振荡流底边界层中拟序涡结构运动演化的大涡模拟研究 [J]. 船舶力学，2002，6(4)：1-13．

Bai Yuchuan，Xu Haijue. Large eddy simulation study for evolution of coherent vortex structure in oscillatory boundary layer flow over flat-plate or winger-type wall[J]. Journal of Ship Mechanics，2002，6(4)：1-13(in Chinese).

［17］ Bai Yuchuan，Ng C O，Huang Tao. A numerical study on the structure and dynamics of turbulence in oscillatory bottom layer flow over a flat or rippled bed[J]. China Ocean Engineering，2006，20(1)：45-60.

［18］ 白玉川，蒋昌波，罗纪生，等. 振荡流底层拟序结构及其与泥沙相互作用研究[J]. 力学进展，2003，33(3)：347-356.

Bai Yuchuan，Jiang Changbo，Luo Jisheng，et al. The progress of research on the coherent structure in oscillatory flow bottom boundary layer and its interaction with the sediment[J]. Advances in Mechanics，2003，33(3)：347-356(in Chinese).

［19］ Shen Y M，Ng C O，Chwang A T. A two-fluid model of turbulent two-phase flow for simulating turbulent stratified flows[J]. Ocean Engineering，2003，30(2)：153-161.

(责任编辑：田 军)

Theoretical Model of Coherent Structure of Oscillatory Flow in Wave Boundary Layer

Chen Hanbao1，Xu Haijue1,2，Bai Yuchuan1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

The coherent structure in the turbulence is a kind of detectable, orderly motion of the fluid. It always appears as the complicated three-dimensional structure in the wall turbulence. With symmetric oscillatory flowas the object of study, a theoretical model that describes its coherent structure was established. The ranges of Reynolds numbers, the wave number of the coherent disturbance and the frequency were investigated. Moreover, the relationship between the two-dimensional disturbance and the three-dimensional disturbance, the symmetric characteristics of the coherence structure and the spatial distribution of the disturbance velocity, Reynolds stress and additional vorticity were analyzed. The results show that the characteristics of the coherent structure of the symmetric oscillatory flow not only are related to such factors as Reynolds number, but also are closely related to the oscillatory frequency.

oscillatory flow；coherent structure；stability characteristics

O353.2

A

0493-2137(2014)03-0267-09

10.11784/tdxbz201212002

2012-11-30；

2013-02-04.

国家自然科学基金创新研究群体科学基金资助项目(51021004)；国家自然科学基金资助项目(51279124，50809045，51009105)；天津大学水利工程仿真与安全国家重点实验室开放基金资助项目.

陈汉宝（1971— ），男，博士研究生，chenhanbao@163.com.

徐海珏，xiaoxiaoxu_2004@163.com.