大体积混凝土施工期冷却水管埋设形式的优化

张 超，常晓林，刘杏红，2

大体积混凝土施工期冷却水管埋设形式的优化

张 超1，常晓林1，刘杏红1，2

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 武汉大学土木建筑工程学院，武汉 430072)

采用冷却水管通水冷却是大体积混凝土坝施工期主要温控措施，而冷却水管埋设布置形式对混凝土内部温度和应力的影响较为显著．利用有限元热流耦合精细算法，考虑了冷却水管中水流与混凝土之间的相互对流热交换机制，真实反映冷却水管附近温度梯度，对冷却水管在仓面上采用不同的布置方式时混凝土内部的温度和应力分布进行详细计算分析．结果表明：相比传统的水管埋设布置方式，采用冷却水管双循环的布置方式更能充分发挥水管冷却作用，且能有效改善混凝土内部的温度和应力分布，降低混凝土内部的温度梯度，对大体积混凝土温控防裂有较为积极的意义．

大体积混凝土；水管冷却；冷却水管埋设；热流耦合算法；温控防裂

大体积混凝土坝施工期温控措施有多种，采用水管通水冷却降温是行之有效的主要温控防裂措施，它能有效降低混凝土内部的最高温度，把混凝土内部温度降低到接缝灌浆温度，同时减小内外温差．工程中广泛采用朱伯芳院士[1]提出的水管冷却的等效算法，其将冷却水管看成负热源，从平均意义上考虑水管的冷却作用，得到水管冷却温度场的近似解，其方法计算简便；然而实际工程中，大多数水管都位于浇筑层面上，采用等效算法不能考虑水管布置及通水方式等因素对混凝土温度及应力分布的影响，会产生较大的误差[2]．闫慧玉[3]采用热流耦合精细算法对水管冷却过程进行了精细模拟，段寅等[4]对水管冷却等效算法与精细算法做了详细的对比分析，其结果表明热流耦合精细算法能真实地模拟水管冷却降温过程，反映混凝土内部温度及应力分布情况．

混凝土温度场自身的非线性、内部数目众多的冷却水管中的流动水体和混凝土热交换以及浇筑层面和表面的散热，导致整个混凝土温度场的计算极为复杂．目前，较多学者对通水冷却时的冷却水温、冷却流量、水管布置形式、水管材料等影响因素进行了深入分析[3-6]，而鲜有学者对水管在仓面的埋设方式进行深入研究．为此，笔者依据理论上严密的有限元热流耦合精细算法，并依托大岗山高拱坝工程建设实际情况，选取典型坝段基础约束区混凝土为研究对象，对采用不同水管埋设方式时该坝段混凝土的内部温度和应力分布进行了计算分析，以了解冷却水管在不同埋设方式时的真实冷却降温作用，并从中得出一些有益的结论，为工程实际中水管冷却温控措施提供参考．

1 热流耦合精细计算原理

根据混凝土热传导理论，瞬态温度场T(x,y,z,τ)在计算中应满足方程

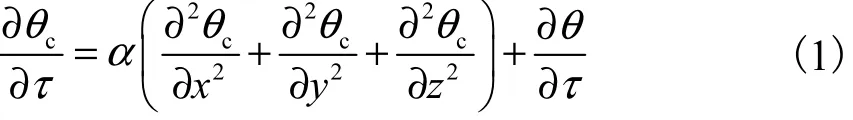
式中：cθ为混凝土的温度；α为材料的导热系数；θ为材料的绝热温升；τ 为龄期．

混凝土通过冷却水进行降温的过程是一个典型的热量在混凝土与冷却水之间进行交换的流固耦合问题，冷却水的流动造成了热量通过对流热交换的方式从混凝土传递到水体并由水流带走，因此，在热流耦合计算过程中，混凝土用三维实体单元模拟，冷却水管采用热流管单元离散，依据管单元附加节点与混凝土实体单元节点耦合来实现冷却水与混凝土的对流热交换，如图1所示．混凝土水管冷却是一个空间温度场问题，在水管冷却边界处发生对流换热，同时由于冷却水管内部热流体的不断运动，它们在移开后的空位又被新的较冷的流体所取代，因而水温将沿冷却水流方向上升．

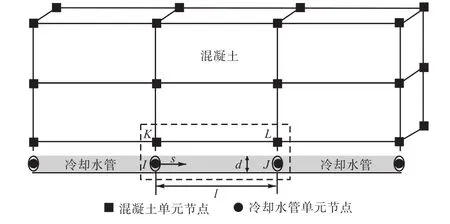
图1 热流耦合精细模型Fig.1 Heat-fluid coupling model

将冷却水管中的水流假定为一维恒定流，根据能量守恒原理，混凝土与冷却水管进行热量交换的过程可采用热流管单元的控制方程表示，即

式中：T为节点温度向量；˙T为变温速率向量；H为热传导矩阵；C为比热矩阵．

基于Fourier定律和能量守恒定律，假设冷却水由节点I流向节点J，水管单元节点I、K处的控制方程可以通过“对流-扩散”模型表示为

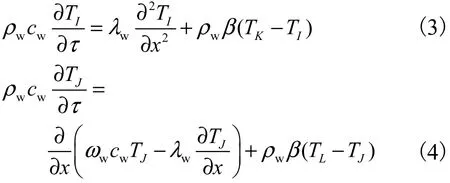
式中：ρw、cw、λw分别为冷却水的密度、比热、热传导系数；ωw为冷却水流量；β为混凝土与冷却水管之间的对流热传导系数．在上述对流热交换过程中，混凝土单元的节点K、L被冷却水管单元I、J吸收的热流量为

对于冷却水管内的对流热传导系数，根据工程实际，计算过程中使用最广泛的一般是Dittus-Boelter公式[7-8]，即

式中：Nu为努塞尔系数，Nu=βd/λ，d为水管管径，当冷却水处于层流区时，Nu可取为3.66；Re为雷诺数，Re=ρdu/μ；Pr为普朗特数，Pr=μc/λ；e1、f、g为常量参数，当管内冷却水处于紊流区时，建议e1=0.023，f=0.8，g=0.33[9]．大体积混凝土通水冷却时，冷却水管进水口水温与混凝土内部温度之间的温差一般在10～15,℃左右，所用水管形式相对固定，内半径一般为0.014,m，外半径为0.016,m，长度在100～300,m之间，冷却水流速一般为0.5,m/s，水管的长度与直径比值范围为7,142～21,428，Re= 115,244，满足Dittus-Boelter方程的使用条件，计算过程中，忽略了努塞尔系数沿水管水流方向的变化．

2 徐变温度应力场

由文献[10]可知，混凝土在复杂应力状态下的应变增量主要由徐变应变增量、弹性应变增量、温度应变增量、自生体积变形增量以及干缩应变增量构成，即

二是建档制度。在制度制约下，内容丰富详实的土地质量档案资料，可在土地利用规划编制、耕地保护及土地交易、土地流转、耕地占补平衡、土地整治、土地质量等级变更、农产品安全源头追溯等方面，发挥重要作用。

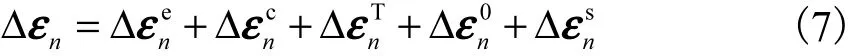
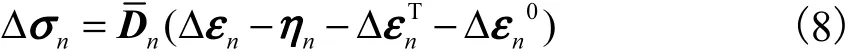
式中：Dn为弹性矩阵；Δεn为节点位移引起的单元应变增量．

3 水管布置优化

3.1 计算条件

笔者选取大岗山高拱坝14#坝段基础强约束区浇筑块为研究对象，该浇筑块顺河向长度为30,m，横河向长度16,m，竖直向长度18,m．竖直方向上混凝土共分为12个浇筑层，每个浇筑层厚度均为1.5,m，水管间距为1.5,m×1.5,m(水平×竖直)；混凝土和基岩采用六面体8节点单元离散，水管采用4节点热流耦合单元离散．为简化计算，取地基和浇筑块的4个侧面绝热边界条件，单根水管长度为310,m．混凝土浇筑温度为15,℃，浇筑间歇期约为10,d；计算时考虑平均情况，外界散热边界条件为年平均气温，取值20.9,℃．应力计算中，坝体荷载包括自重和施工期的温度荷载，基岩底面3向全约束，左右侧面及上下游面为法向单向约束，坝段的4个侧面均为自由面．图2为混凝土及基础有限元模型．图3为浇筑层及水管单元有限元模型．

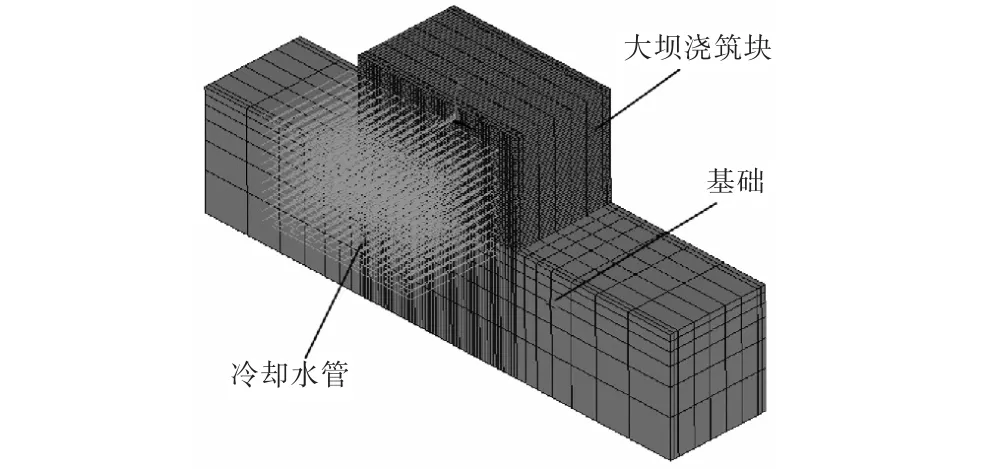
图2 混凝土及基础有限元模型Fig.2 Finite element model of concrete and rock

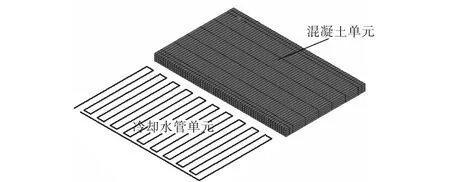
图3 浇筑层及水管单元有限元模型Fig.3 Finite element model of concrete and cooling pipes

大岗山高拱坝14#坝段基础强约束区所采用的常态混凝土C18036绝热温升可用朱伯芳院士[10]提出的复合指数公式进行拟合，即

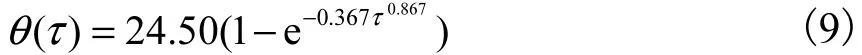
C18036常态混凝土的徐变度的拟合公式[11-12]为

表1 混凝土热力学参数Tab.1 Thermal parameters of concrete

表2 冷却水热力学参数Tab.2 Thermal parameters of cooling water

表3 混凝土力学参数Tab.3 Mechanical parameters of concrete

3.2 水管埋设方式

根据位置不同，大体积混凝土坝体内部冷却水管通常选用外径30,mm、壁厚1.6,mm的钢管或者外径32,mm、壁厚2,mm的高强度聚乙烯塑料管(HPDE管)．冷却水管在铅直方向上可按照梅花形或矩形布置，由于梅花形布置在施工过程中不太好控制，因此实际工程中通常采用矩形布置；在仓面上冷却水管通常采用蛇形布置，如图4所示．实际工程中冷却水管进、出水口往往是固定的，由于大坝施工过程中多仓混凝土冷却水管同时共用1根冷却水引水管道，变换某仓混凝土冷却水进出口方向往往需要耗费较大的人力、物力．笔者在计算中考虑了1种在仓面上以“双循环”方式进行通水冷却的水管，并与实际施工过程中采用的水管“单循环”冷却方式的冷却效果进行了比较分析，如图5所示．

图4 仓面冷却水管蛇形布置Fig.4 Serpentine layout of cooling pipe on layer

图5 不同冷却水管埋设方式有限元模型Fig.5 Finite element model of different cooling pipe layouts

3.3 温度场仿真结果

大岗山高拱坝基础约束区混凝土在一期通水冷却过程中，水管进水口温度为12～14,℃，通水冷却持续时间约为21,d，二期冷却从混凝土龄期大于90,d之后开始进行，二期冷却通水温度为13,℃，封拱灌浆温度为14,℃；采用不同循环方式时混凝土温度场仿真计算结果如图6～图10所示．

从计算结果来看，当采用两种不同的冷却水冷却循环方式时，不同时刻、距水管进水口不同距离处冷却水温度变化曲线如图6所示；伴随着冷却水的流动，混凝土内部的热量将不断被冷却水带走，冷却水温度将沿程上升；在混凝土浇筑后3,d，由于混凝土中水泥水化热作用较为显著，冷却水与混凝土之间对流换热作用强烈，因此冷却水沿程温升较为明显，水管出水口处温度比进水口处高5～7,℃；而在混凝土浇筑后15,d左右，经过一段时间的通水冷却，混凝土内部温度逐渐降低且水泥水化热作用减弱，水管冷却效果有所降低，水管中水流带走的热量逐渐减少，水管进、出水口温差也有所降低，约为3～4,℃．对比两种不同循环方式水管沿程温度变化情况可知，在混凝土浇筑后3,d左右，采用双循环的方式水管出口处温度比单循环方式要高1,℃左右，在浇筑后15,d左右要高0.3～0.5,℃，这说明采用双循环的冷却方式冷却水对混凝土的控温削峰作用更为明显．

图6 水管水温沿程温度变化Fig.6 Temperature of cooling water along pipe

图7 不同水管埋设方式混凝土最高温度包络图Fig.7Maximum temperature envelope of concrete with different cooling pipe layouts

考虑到水管中冷却水沿程温度上升以及混凝土内部温度随时间变化，冷却过程中单循环冷却方式下混凝土内部最高温度约为28.2,℃，在相同条件下的双循环冷却方式下混凝土内部最高温度约为27.1,℃．靠近水管进水口的位置处，混凝土温度值偏低，远离进水口的地方，混凝土温度值较高．

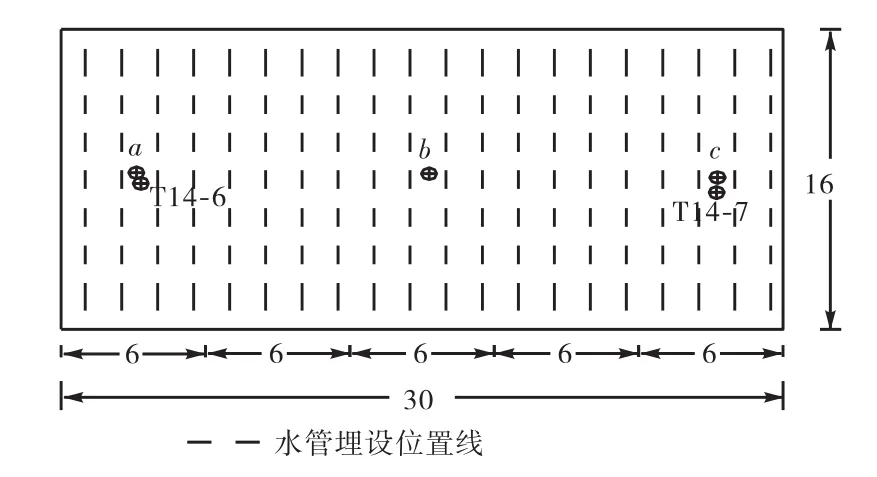
图8 仓面典型点及温度计埋设位置示意Fig.8 Position of typical points and thermometers on layer

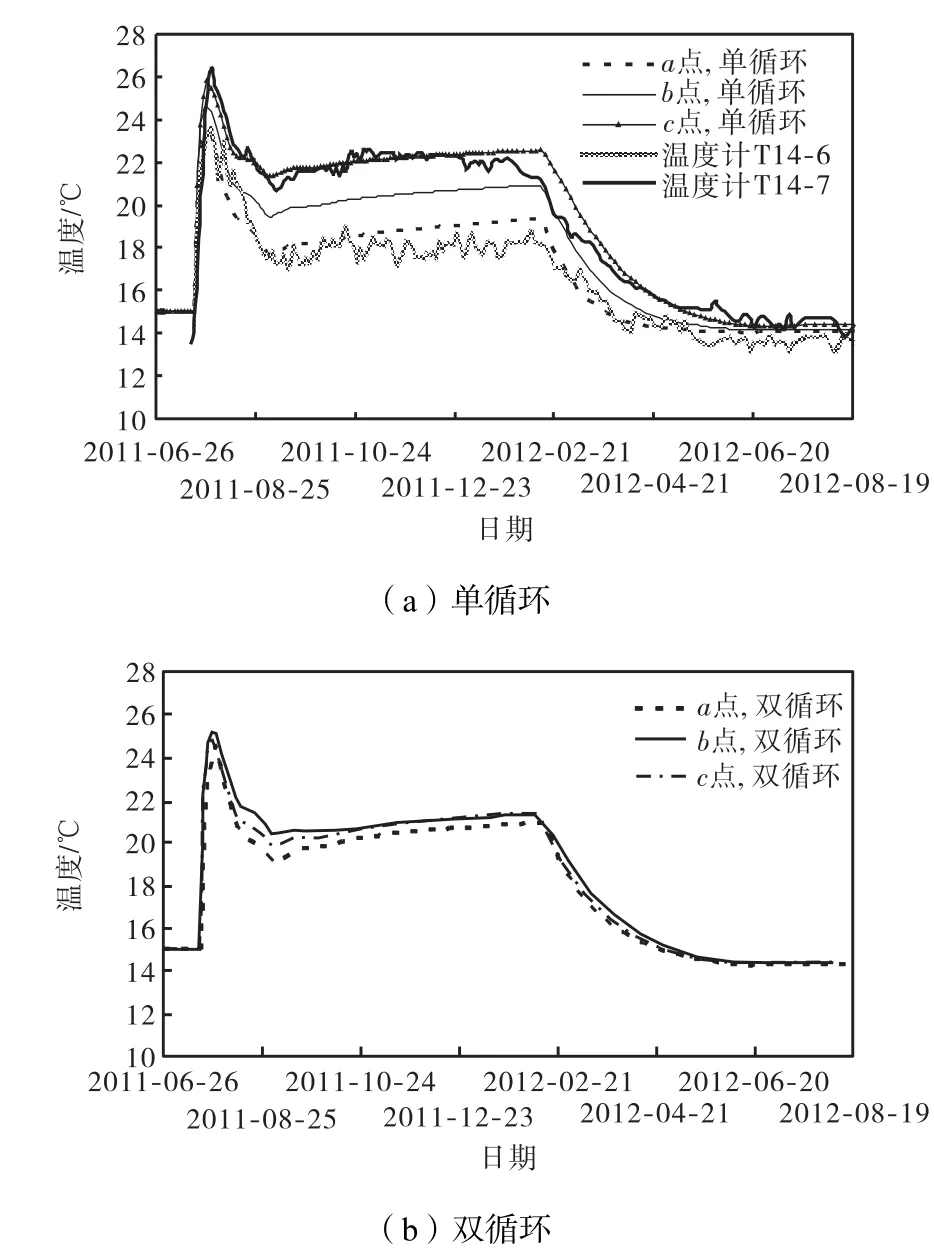
图9 不同循环方式典型点温度历程曲线Fig.9 Temperature duration curves of typical point by different cooling pipe layouts

混凝土内部温度分布与冷却水管埋设方式有关．从典型点的温度历程曲线可知，采用单循环的方式，仿真温度与实测温度变化过程吻合良好，混凝土内部温度沿水流方向呈梯度分布较为明显，靠近水管进水口位置处的a点混凝土内部最高温度值较低，约为23.5,℃，而远离水管进水口位置的c点，混凝土内部最高温度值相对较高，约为26,℃；靠近水管进水口附近，一期冷却温降幅度约为6～7,℃，而远离水管进水口位置时，一期冷却温降幅度约为4,℃．采用双循环的埋设方式时，混凝土内部温度分布相对较均匀，abc、、3个特征点最高温度均在25,℃左右，一期冷却温降幅度约为5,℃．在早龄期，由于混凝土水化热作用显著，混凝土内部温升较快，靠近水管进水口附近的混凝土温度值相对较低，而远离混凝土进水口位置温度较高，且这种差别在层面处更为明显；在一期通水冷却持续一段时间后，混凝土内部最高温度有了明显的降低；从一期通水结束后混凝土温度场分布可知，一期通水冷却结束后，混凝土内部温度分布较不均匀，靠近水管进水口处混凝土温度比远离进水口处要低3～4,℃．当采用双循环的冷却方式时，考虑到水管沿程温度上升，水管和混凝土之间的对流换热作用更为明显，水管所在层面处混凝土内部最高温度比单循环温度要低，且在通水冷却过程中，混凝土内部各区域温度分布也更加均匀，由此可知，双循环方式有效改善了混凝土内部温度分布．

图10 冷却水管所在层面处通水3,d后的温度云图Fig.10Temperature contour of concrete with coolingwater after three days

3.4 应力场仿真结果

图11 不同水管埋设方式混凝土最大拉应力包络图Fig.11 Maximum tensile stress envelope of concrete with different cooling pipe layouts

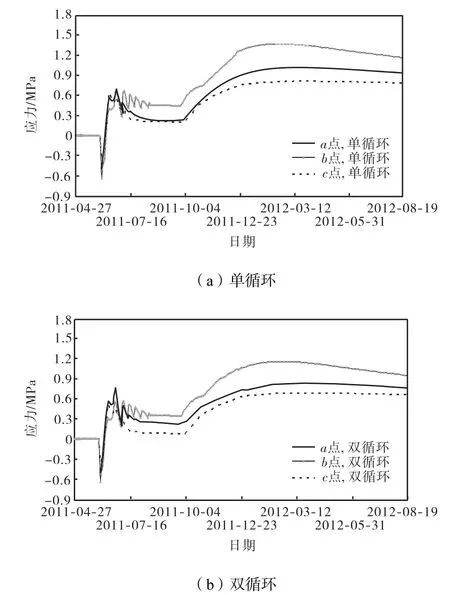
图12 不同循环方式特征点应力历程曲线Fig.12 Stress duration curves of typical points with different cooling pipe layouts

图11 和图12为应力仿真计算结果．从图中可知，采用单循环方式，浇筑块内部最大应力值约为1.6,MPa，而采用双循环方式，混凝土内部最大应力值比单循环方式小0.2～0.3,MPa，其最大值约为1.39 MPa，最大拉应力主要发生在内部顺河向中心处；在混凝土浇筑初期，约5,d左右，由于混凝土水化热温升值较高，混凝土内部一直是压应力，随着冷却水冷却效果的显现，混凝土内部由压应力转变为拉应力，最大应力值发生在二期通水结束时刻，靠近中心部位的b点的应力值比较大，而靠近两边的ac、点应力值相对偏低．采用双循环方式时，从图10可以看出，由于混凝土进水口和出水口位置较近，在一期冷却过程中，该区域混凝土内部温度梯度较大；从图11 和图12可知，在该区域的典型点a在一期冷却过程中拉应力值也较大，约为0.85,MPa，而采用单循环方式时a点的拉应力约为0.68,MPa．而从混凝土内部整体应力分布来看，采用双循环方式混凝土内部温度分布更加均匀，二期通水结束后，其最大拉应力比单循环方式要低，且混凝土内部应力分布也更均匀．

4 结 论

本文结合大岗山高拱坝工程的建设实际，采用水管冷却热流耦合精细算法对大体积混凝土采用冷却水管冷却时的水管埋设方式进行了计算分析，结果表明：

(1) 相比于传统单循环的水管埋设方式，采用双循环方式布置时，水管冷却降温效果更为明显，且更能有效改善混凝土内部温度分布，降低混凝土内部温度梯度；

(2) 相比于传统单循环的水管埋设方式，采用双循环布置时，混凝土内部最大拉应力值要低，这对大体积混凝土温控防裂更为有利；

(3) 采用双循环的冷却方式，易在水管进出口位置附近形成较大温度梯度，因此，通水冷却降温时，应严格控制冷却水温度．

［1］ 朱伯芳. 考虑水管冷却效果的等效热传导方程[J]. 水利学报，1991(3)：28-34.

Zhu Bofang. Equivalent equation of heat conduction in mass concrete considering the effect of pipe cooling[J]. Journal of Hydraulic Engineering，1991(3)：28-34(in Chinese).

［2］ 朱伯芳. 混凝土坝水管冷却仿真计算的复合算法[J].水利水电技术，2003，34(11)：47-50.

Zhu Bofang. Compound methods for computing the effect of pipe cooling in concrete dam[J]. Water Resources and Hydropower Engineering，2003，34(11)：47-50(in Chinese).

［3］ 闫慧玉. 大体积混凝土温度场水管冷却热流耦合仿真方法研究[D]. 武汉：武汉大学水利水电学院，2005.

Yan Huiyu. Study on Thermal-Fluid Simulation Methodof Water Pipe Cooling for the Temperature Field of Mass Concrete[D]. Wuhan：School of Water Resources and Hydropower Engineering，Wuhan University，2005(in Chinese).

［4］ 段 寅，向正林，常晓林，等. 大体积混凝土水管冷却热流耦合算法与等效算法对比分析[J]. 武汉大学学报，2010，43(6)：703-707.

Duan Yin，Xiang Zhenglin，Chang Xiaolin，et al. Comparative analysis of pipe cooling in mass concrete using thermal fluid coupling method and equivalent method based on FEM[J]. Engineering Journal of Wuhan University，2010，43(6)：703-707(in Chinese).

［5］ 朱伯芳，蔡建波. 混凝土坝水管冷却效果的有限元分析[J]. 水利学报，1985(4)：28-34.

Zhu Bofang，Cai Jianbo. Finite element analysis of the effect of pipe cooling in concrete dams[J]. Journal of Hydraulic Engineering，1985(4)：28-34(in Chinese).

［6］ 谢详明，郭 磊. 高温地区碾压混凝土重力坝的施工期温度裂缝控制[J]. 天津大学学报，2011，44(6)：504-510.

Xie Xiangming，Guo Lei. Thermal cracking control of RCC gravity dam constructed in high air temperature and dry area[J]. Journal of Tianjin University，2011，44(6)：504-510(in Chinese).

［7］ Myers T G，Fowkes N D，Ballim Y. Modeling the cooling of concrete by piped water[J]. Journal of Engineering Mechanics，2009，135(12)：1375-1387.

［8］ Park B C，Cho Y I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles[J]. Experimental Heat Transfer，1998，11(2)：151-170.

［9］ Kim Jin Keun，Kim Kook Han，Yang Joo Kyong. Thermal analysis of hydration heat in concrete structure with pipe-cooling system[J]. Computers and Structures，2001，79(2)：163-171.

［10］ 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京：中国电力出版社，1999.

Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing：China Electric Power Press，1999(in Chinese).

［11］ 刘杏红，周 伟，常晓林，等. 改进的非线性徐变模型及其在混凝土坝施工期温度应力仿真分析中的应用[J]. 岩土力学，2009，30(2)：440-446.

Liu Xinghong，Zhou Wei，Chang Xiaolin，et al. An ameliorative nonlinear creep model and its application to thermal stress simulation during construction period[J]. Rock and Soil Mechanics，2009，30(2)：440-446(in Chinese).

［12］ Machida N，Uehara K. Nonlinear thermal stress analysis of a massive concrete structure[J]. Computers and Structures，1987，26(2)：287-296.

(责任编辑：赵艳静)

Optimization of Cooling Pipe Layout in Mass Concrete During Construction Period

Zhang Chao1，Chang Xiaolin1，Liu Xinghong1,2
(1. State Key Laboratory of Water Resources and Hydropower Engineering，Wuhan University，Wuhan 430072，China；2. School of Civil and Architectural Engineering，Wuhan University，Wuhan 430072，China)

Pipe cooling is the main measure to control the temperature of mass concrete in the construction period，and the layout of cooling pipe has obvious influence on the internal temperature and stress of mass concrete. In this paper，a heat-fluid coupling finite element method is presented to simulate the pipe cooling of mass concrete. The method takes the heat exchange mechanism between cooling water and concrete into consideration which can accurately reflect the temperature gradient around the cooling pipe. The calculation results show that compared with conventional pipe layout，the layout of double circulating can make more sufficient use of the cooling pipe，effectively improve the distribution of internal temperature and stress，and obviously decrease the internal temperature gradient in mass concrete.

mass concrete；pipe cooling；cooling pipe layout；heat-fluid coupling method；temperature control and crack prevention

TV52

A

0493-2137(2014)03-0276-07

10.11784/tdxbz201205050

2012-05-18；

2012-09-12.

国家自然科学基金资助项目(50909078).

张 超（1988— ），男，博士研究生，gonopo2006@126.com.通讯作者：常晓林，changxl@whu.edu.cn.