基于全相位窄带滤波的超分辨率时延估计

闫 格，黄翔东，刘开华

基于全相位窄带滤波的超分辨率时延估计

闫 格，黄翔东，刘开华

(天津大学电子信息工程学院，天津 300072)

为提高超分辨率时延估计的抗噪性能，提出了基于全相位窄带滤波的超分辨率时延估计算法．在陷波器设计方法基础上，设计出中心频点可精确控制的具有类点通传输特性的窄带滤波器，然后用该滤波器对存在时延关系的两路采样序列进行滤波处理，再依照传统相位差时延估计法，即可获得高精度时延估计．仿真实验表明：相比于基于信号重心插值的超分辨率时延估计法，该方法信噪比范围要高出10,dB，具有广阔的工程应用前景．

时延估计；窄带滤波器；全相位；超分辨率

对于“超分辨率”时延估计问题，由于对时延的“分辨力”的界定不同，目前学术界对超分辨率时延估计问题存在两种理解，两者都是从两路信号的互相关函数的区分能力出发[1-2]．第1种理解是针对宽带信号而言，把时延估计的分辨率与信号带宽B联系在一起，如在文献[3-4]中，认为时延估计分辨力的极限为带宽B的倒数，也就是说，互相关函数无法区分相对时延小于1/B的两路信号，这类超分辨率时延估计已有国内外学者做了大量研究[5-6]；第2种理解是针对窄带信号而言，把时延估计的分辨力与采样速率fs联系在一起，认为时延估计的分辨力的极限是采样间隔Ts=1/fs，也就是说，互相关函数无法区分相对时延小于Ts=1/fs的两路信号，目前这类超分辨率时延估计主要以时域内插法为主(如文献[7]提出的Lagrange内插，文献[8]提出的ASDF内插，文献[9]提出的基于信号重心估计的ASDF内插等)，然而这类超分辨率时延估计法虽然可获得亚采样间隔(subsample)的估计精度，但由于是在时域内进行估计，故抗噪性能差，不适合于低信噪比情况．从定量角度来看，第2种超分辨率时延估计要求高更些(如对于第1种情况，文献[3]的仿真实验中设定的时延间隔仍为Ts的整数倍，而第2种情况文献[9]中设定的时延间隔则为Ts的小数倍)，本文讨论的是第2种情况．

对于两路窄带信号，为实现超出一个采样间隔的时延估计分辨率，文献[9]提出了结合重心与均方差函数内插的估计方法，该方法先求出第1路信号的重心位置，然后计算第1路信号与延迟整数倍采样间隔后的第2路信号的均方误差，取出最小均方误差对应的整数倍时延，代入固定的内插公式而算出真正时延．然而文献[9]的实验表明，该方法在高信噪比时具有很高的精度；但在信噪比小于15,dB时，会出现较大的时延估计误差．

利用两路信号的相位差信息求时延，也是超分辨率时延估计的一个重要途径[10-11]．众所周知，相位对噪声具有敏感性，因而直接采用相位差方法同样难以适用于信噪比较低的场合．然而噪声能量分布是宽频段的，而信号能量分布是窄带的，如果可以设计出恰好能提取信号主要成分的窄带数字滤波器，则可把噪声的影响大大降低，也为超分辨率时延估计的提供可能．数字滤波器可分为无限冲激响应(infinite impulse response，IIR)滤波器和有限冲激响应(finite impulse response，FIR)滤波器两种，但是IIR滤波不具有线性相位特性，而且会破坏信号的时延关系，故只宜采用FIR滤波器．如何设计中心频点可任意控制的窄带FIR滤波器是超分辨率时延估计的关键，文献[12-13]中设计了全相位FIR陷波器，解决了窄带滤波器的中心频点精确控制问题，本文在此基础上设计出具有类点通传输特性的窄带滤波器，基于此在频域中计算两路信号相位差，不仅取得了很好的超分辨率时延估计效果，而且提高了抗噪性能．

1 问题描述

设y1(t)和y2(t)分别为两路具有时延的信号，且有

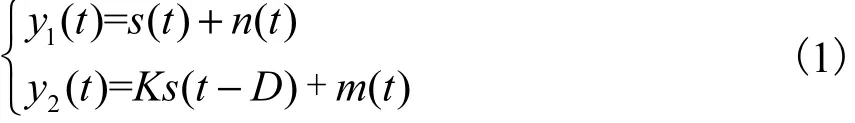
式中：s(t)为发射信号；K为幅度衰减因子；n(t)和m(t)为加性干扰信号；D为要估计的时延量．

显然，式(1)中的时延量D是指群延时．若不考虑噪声，令所关心的频率为f，对x1(t)和x2(t)进行理想傅里叶变换(分别为X1(2,πf)和X2(2,πf))，根据傅里叶变换的时移与相移的关系，有

令傅里叶变换X1(2πf )与X2(2πf )的相位谱为φ1(f )与φ2(f )，则有

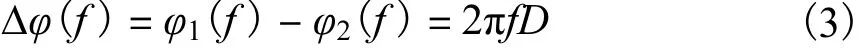
从而有

因而只要求出某频点f上两路信号的相位谱差值，由式(4)就可以很容易地求出时延估计．需指出的是，由于基于相位差做时延估计，故要求式(4)的时延估计值D小于信号周期，否则会出现相位整周模糊问题，从而引入测相的不确定性．

然而信号采样后，在存在噪声的场合，直接做FFT按照式(4)求出的相位差变得不准确．对信号做窄带滤波处理后，会改善相位差测量的方差，因而窄带滤波是关键．

2 全相位窄带类点通FIR滤波器设计

文献[12-13]中解决了中心频点可精确控制的全相位FIR陷波器设计问题．假设滤波器阶数为N(最终全相位FIR滤波器长度为2,N-1)[12-13]，文献[12]指出，只需代入式(5)所示的解析公式，即可设计出数字中心频率为ω0处的陷波器，即

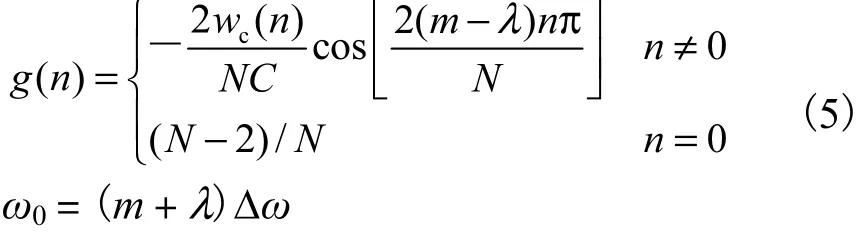
式中：wc(n)为卷积窗(由矩形窗与另一对称窗卷积而成[1-2])；m为整数，代表中心频点的粗略位置；λ为中心频点的精确位置．

用全通滤波器系数δ(n)减去g(n)，即可得到与陷波器互补的具有类点通特征的窄带滤波器系数h(n)，即

例1 令N=32，m=2，λ=0.4，分别代入式(5)和式(6)，可得陷波器系数g(n)和类点通滤波器系数h(n)，分别求其幅频响应，得到其幅频曲线|G(ω)|和|H(ω)|如图1和图2所示.

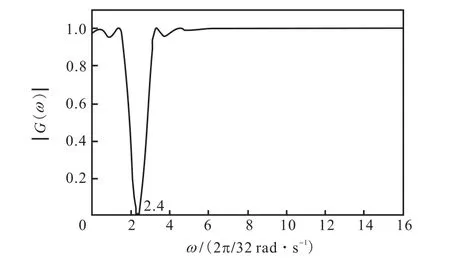
图1 陷波器幅频曲线Fig.1 Amplitude-frequency curve of notching filter

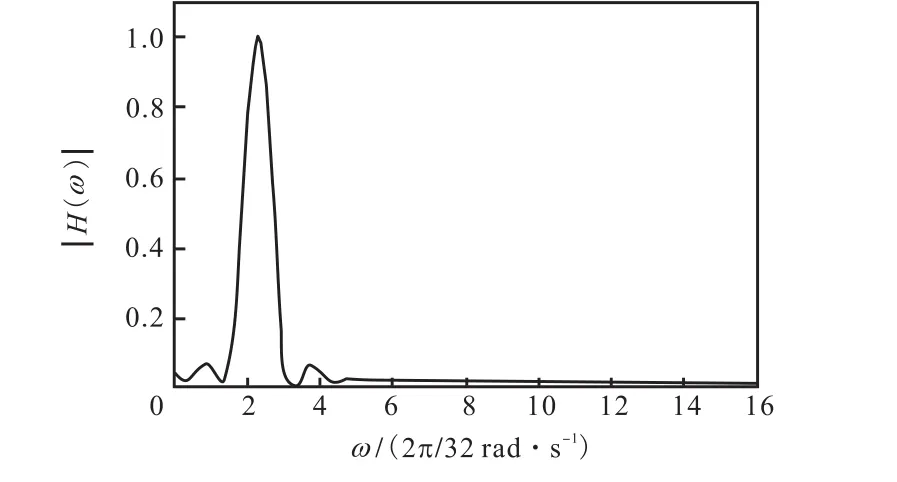
图2 类点通滤波器幅频曲线Fig.2 Amplitude-frequency curve of similar point-pass filter

从图1和图2可以看出，陷波器和类点通滤波器的中心频点被精确地设定在ω0=(m+λ)Δω= 2.4Δω的位置；而类点通滤波器则可以用来获得单频成分的信号输出，在时延估计中有很大作用．

3 类点通滤波器对含噪信号的影响

3.1 类点通滤波器的滤波效果

例2 比较余弦波s1(t)=cos(2,πf0,t+θ0)与s2(t)=s1(t-D)=cos(2,πf0(t-D)+θ0)的不含噪采样情况、含噪情况及其类点通滤波后的波形(θ0=50°，f0=2.4,Hz，采样速率fs=32,Hz，故采样间隔Ts=1/fs= 1/32 s，时延量D=3.2,Ts)．

不含噪情况的采样波形s1(n)、s2(n)波形描绘如图3(a)所示，可以看出，s1(n)、s2(n)的样点分布可以反映出恒定时延．

对余弦序列s1(n)、s2(n)，加入方差为1的随机噪声ξ(n)，则其信噪比SNR=10,lg(1/2)=-3,dB，从而得到含噪序列y1(n)=s1(n)+ξ(n)，y2(n)= s2(n)+ξ(n)，波形如图3(b)所示．可以看出，由于噪声干扰，y1(n)、y2(n)的样点分布无法反映恒定时延．

令N=32，m=2，λ=0.4，代入式(6)获得类点通FIR滤波器系数，再分别对含噪序列y1(n)、y2(n)进行滤波，其滤波输出s′1(n)、s′2(n)如图3(c)所示．可以看出，除轻微的幅度失真外，恢复的波形s′1(n)、s′2(n)基本与无噪波形s1(n)、s2(n)样点分布一致，能反映出恒定时延．

以上仿真实验说明，若确知中心频率，依据式(6)即可获得设计出类点通滤波器，再对含噪信号滤波后，可以恢复易于提取时延信息的信号，在此基础上再做时延估计，有望获得很高的估计精度．

3.2 类点通滤波器对相位差估计的影响

将例2中图3的各序列分别作FFT，取其模值可得如图4所示的振幅谱，取其两路相位谱再求差值后，可得如图5所示的相位差谱．

图3 不同情况下两时延序列的样点分布Fig.3Distrbution of two secquences with delay relationship in different cases

从图4(b)的振幅谱可以看出，由于噪声干扰，其振幅谱与相位差谱与无噪声情况差别很大；而从图4(c)的振幅谱可以看出，经过类点通滤波后，其振幅谱基本恢复，而相位差谱仅与滤波前存在细微差别．

观察主谱线位置k=m=2处的相位差值Δφ12(2)，由于相位差为频率对时间的累积，理想情况下两路信号的相位差是Δφ12=2,πf0D=2,π×2.4×(3.2×1/32)= 1.508,rad=86.4°．因所取阶数N=32较小，且余弦信号存在两个边带而相互影响，图5(a)的相位差值Δφ12(2)=93.4°，而由于噪声干扰影响，图5(b)的相位差值Δφ12(2)=73.6°，存在较大偏差，经类点通滤波后，图5(c)的相位差值Δφ12(2)=95.3°，偏差大大减小．可见，经过类点通滤波后，相位差值估计更为准确．

图4 不同情况下振幅谱的比较Fig.4 Comparison of amplitude spectra in different cases

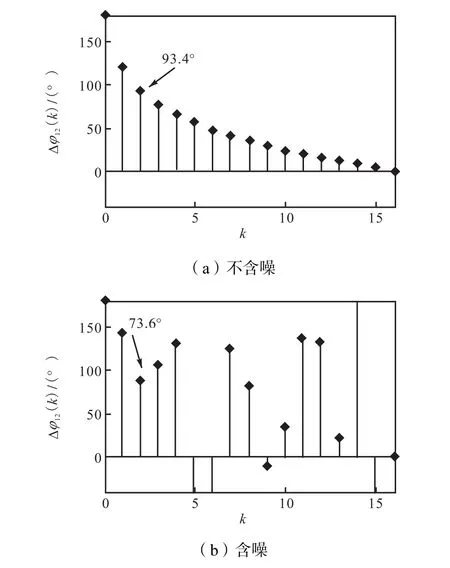
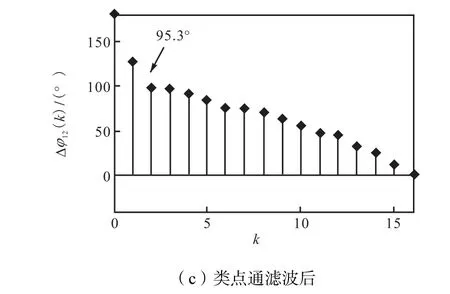
图5 不同情况下相位差谱的比较Fig.5 Comparison of phase-difference spectra in differentcases

为衡量类点通滤波对相位差测量的稳定性，在不同信噪比下分别进行1,000次蒙特卡洛模拟，将所测得的相位差的方差做统计，其结果如表1所示．从表1可以看出，在不同噪声干扰强度下，类点通滤波后的相位差统计方差都比直接相位差测量小得多(最小情况时SNR=-2,dB，仅约为滤波前的1/3)．

表1中的数值表明，引入全相位窄带滤波器后，可以大大提高相位差估计性能，再依据

就可得到时延估计．窄带滤波的引入提高了相位差的估计精度，故有望提高时延估计精度．

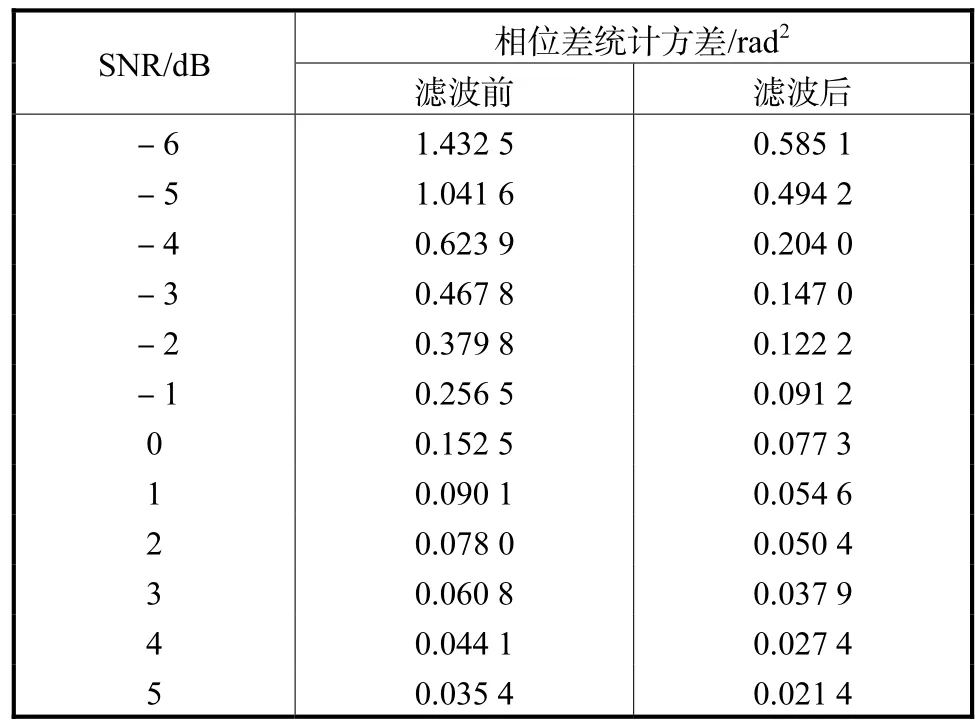
表1 不同信噪比下的相位差统计方差Tab.1 Statistical variance of phase-difference with SNR

4 基于全相位窄带滤波的时延估计算法

基于以上全相位窄带类点通滤波对相位差的分析，本文提出如图6所示的时延估计算法．

图6中，需将中心数字角频率ω0值代入式(6)得到全相位类点通滤波器系数h(n)，用该滤波器分别对两路含噪信号进行滤波，再对其输出分别作FFT，取峰值谱线相位的差值即得Δφ12，再除以ω0即可获得时延估计ˆ．

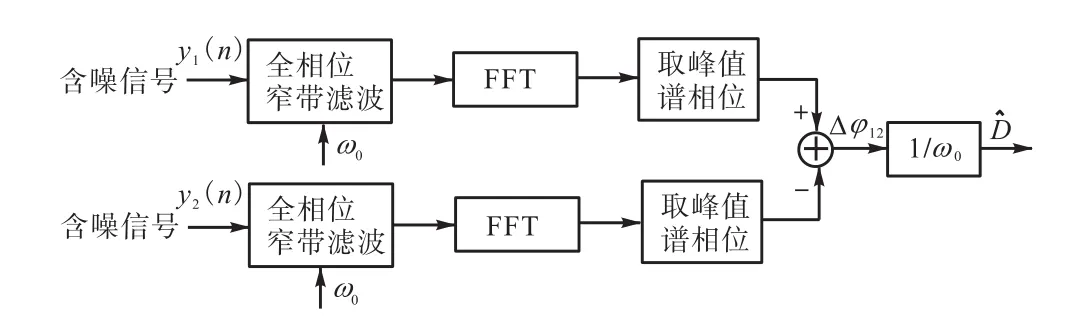
图6 基于全相位窄带滤波的时延估计Fig.6 Time delay estimation based on all-phase narrowband filtering

5 实验验证及分析

例3 对超声窄带信号(α=109，f0=250,kHz，A=105，ξ(t)高斯白噪声)，有

以fs=20,MHz的速率进行采样获得序列s(n)，令时延估计的真实值D=33.6,Ts，阶数N取为1,204．在信噪比SNR∈[0，50],dB的区间内改变噪声ξ(t)的强度，分别按照文献[9]中的超分辨率时延估计法和本文方法进行时延估计，其中对于每一次SNR情况进行200次蒙特卡洛模拟，对每一种SNR情况统计其估计标准差，可得到如图7所示的曲线．

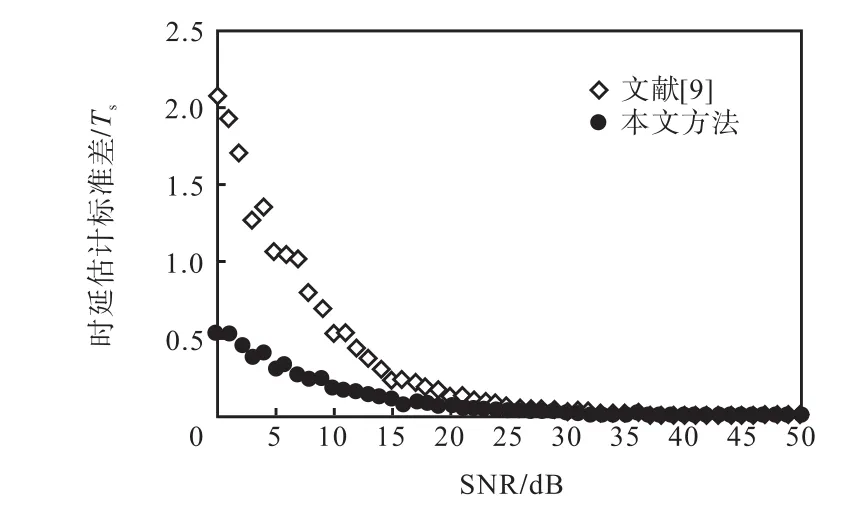
图7 两种算法的时延估计标准差随信噪比变化曲线Fig.7 Curves of standard variations of TDE with SNR for two algorithms

从图7可以看出，当信噪比SNR≥25,dB时，两种算法均可获得很高的时延估计精度，其估计标准差小于0.05,Ts，即实现了超分辨率(即采样间隔Ts)的时延估计，其中本文方法的时延估计标准差比重心插值法稍低些，但优势不大．究其原因，是因为在高信噪比场合，由于噪声干扰小，因而重心插值法在估计信号重心位置是准确的，基于此搜索的两路间最小均方误差对应的整数倍位置也准确，代入插值公式也可以获得高精度、超分辨率的实验估计．

当10,dB≤SNR＜25,dB时，为更深刻地解释两种算法的估计精度，图8给出了SNR=10,dB时，无噪情况、受噪声干扰及全相位窄带滤波后的信号波形．从图8(b)可以看出，当SNR=10,dB时，超声窄带信号存在较严重的波形失真，从而会导致波形重心位置估计出现偏差，而从失真信号经过全相位窄带滤波后得到的波形可看出：窄带滤波输出仍为较纯正的正弦波信号，受到噪声干扰的影响很小，故图7中SNR∈[10，25)dB段的本文方法的时延估计标准差仍小于0.2,Ts，属于较精确的超分辨率估计范畴；而该段的重心插值法得到的时延估计误差则比本文方法大得多(误差为本文方法的2倍以上)．

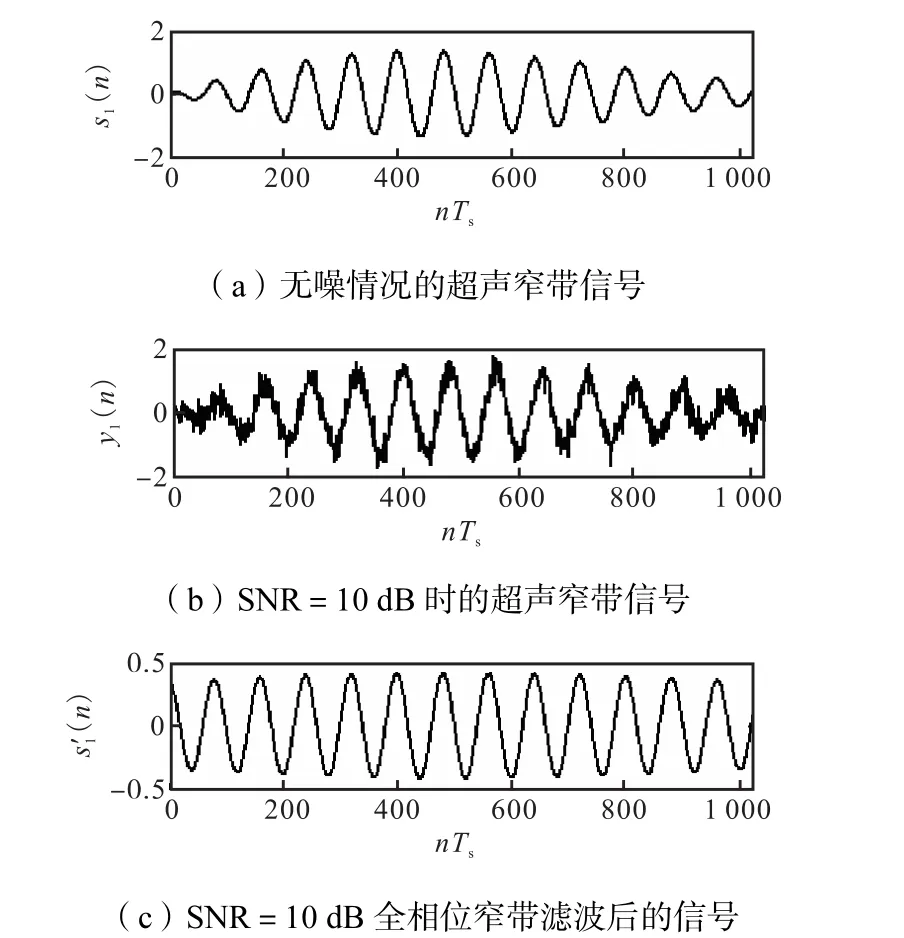
图8 不同噪声干扰及窄带滤波后的波形对比Fig.8Waveform comparison under noisy disturbances and narrow-band filtering

当0≤SNR＜10,dB时，从图7可看出，重心插值法的时延估计的标准差急剧超出0.5,Ts，在SNR= 0,dB时，其标准差达到2.0,Ts以上，已基本失去超分辨率时延估计的意义．而随着信噪比变小，本文方法的误差虽然也增大，但增速没有重心插值法快，大多数SNR情况下其时延估计标准差仍小于0.5,Ts，故仍可粗略地用作超分辨率时延估计．

综上所述，由于噪声是宽带分布的，因而用可精确控制中心频点的窄带滤波后，噪声对有用信号的干扰大大减小，保证了本文方法在SNR较小的场合仍具备较高的超分辨率估计精度．

6 结 语

本文提出基于全相位窄带滤波的相位差时延估计方法，其核心措施是把中心频带可精确设置的全相位类点通滤波器引入到含噪波形的预处理中，再结合传统的相位差时延估计法获得了很高的估计精度．该方法充分利用了宽带分布的噪声对包含有用成分的窄带信号影响较小的特点，从而保证了本文方法具有较高的抗噪性能，实验表明本文方法的SNR适用范围比重心插值法放宽了10,dB．

需要指出的是，本文方法有个前提，那就是需获知信号中心频率位置的先验信息(要求采样速率不能太高)，在很多工程场合(如超声波定位)，其发射信号的中心频率是预先知道的，因而本文方法仍具有较广阔的应用前景．

［1］ Knapp C H，Carter G C. The generalized correlation method for estimation of time delay[J]. IEEE Trans on Acoustics，Speech，and Signal Processing，1976，24(4)：320-327.

［2］ 王 江，杨景曙. 频差存在时广义相关时延估计方法研究[J]. 信号处理，2008，24(1)：112-114.

Wang Jiang，Yang Jingshu. The research of time delay estimation method of general cross correlation with frequency difference[J]. Signal Processing，2008，24(1)：112-114(in Chinese).

［3］ Wu R，Li J. Time-delay estimation via optimizing highly ocsillatory cost functions[J]. IEEE Journal of Oceanic Engineering，1998，23(3)：235-244.

［4］ Wu R，Li J，Liu Z. Super resolution time delay estimation via MODE-WRELAX[J]. IEEE Trans on Signal Processing，1999，35(1)：294-307.

［5］ Ge Fengxiang，Shen Dongxu，Peng Yingning，et al. Super-resolution time delay estimation in multipath envioronments[J]. IEEE Trans on Circuits and Systems (I)：Regular Papers，2007，54(9)：1977-1986.

［6］ Li Jing，Pei Liang，Cao Maoyong，et al. Superresolution time delay estimation algorithm based on the frequency domain channel modelin OFDM systems[C]// Proceedings of the 6th World Congress on Intelligent Control and Automation. Dalian，China，2006：5144-5148.

［7］ Dooley S R，Nandi A K. Adaptive subsample time delay estimation using Lagrange interpolators [J]. IEEE Signal Processing Letters，1999，6(3)：65-67.

［8］ Jacovitti G，Scarano G. Discrete time techniques for time delay estimation[ J]. IEEE Trans on Signal Processing，1993，41(2)：525-533.

［9］ 丁向辉，李 平，孟晓辉. 结合信号重心与ASDF估计超声窄带信号延时[J]. 数据采集预处理，2011，26(6)：718-722.

Ding Xianghui，Li Ping，Meng Xiaohui. Time delay estimation using ASDF and center of gravity for narrowband ultrasonic signals[J]. Journal of Data Acquisition & Processing，2011，26(6)：718-722(in Chinese).

［10］ Viola F，Walker W F. A comparison between splinebased and phase-domain time-delay estimation[J]. IEEE Trans on Ultrasonics，Ferroelectrics and Frequency Control，2006，53(3)：515-517.

［11］ 邱天爽，尤国红，沙 岚，等. 一种基于频差补偿的相位谱时延估计方法[J]. 大连理工大学学报，2012，52(1)：90-94.

Qiu Tianshuang，You Guohong，Sha Lan，et al. A phase spectrum time delay estimation method based on frequency difference compensation[J]. Journal of Dalian University of Technology，2012，52(1)：90-94(in Chinese).

［12］ Huang Xiangdong，Chu Jinghui，Lü Wei，et al. Simplified method of designing FIR filter with controllable center frequency[J]. Transactions of Tianjin University，2010，16(4)：262-266.

［13］ 黄翔东，王兆华. 陷波频率点可精确控制的高效FRM陷波器设计[J]. 系统工程与电子技术，2009，31(10)：2320-2322.

Huang Xiangdong，Wang Zhaohua. Design of highefficiency FRM notch filter with frequency point accurately controlled[J]. Journal of Systems Engineering and Electronics，2009，31(10)：2320-2322(in Chinese).

(责任编辑：金顺爱)

Super-Resolution Time Delay Estimation Based on All-Phase Narrow-Band Filtering

Yan Ge，Huang Xiangdong，Liu Kaihua
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

To enhance the anti-noise performance of super-resolution time delay estimators，one novel time-delay estimator based on all-phase narrow-band filtering was proposed. First，based on the design of notching filter，a narrow-band filter characterized with similar point-pass transfer curve was designed. Secondly，two sequences with delay relationship were processed by this filer. Finally，implementing conventional phase-difference estimating flow yielded a high-precision time delay estimation. Simulation results showed that，compared with the gravityinterpolation method，the proposed method enlarges the SNR application range by 10 dB. Therefore the proposed method has a wide prospect of applied engineering.

time delay estimation；narrow-band filter；all-phase；super-resolution

TP274

A

0493-2137(2014)03-0249-06

10.11784/tdxbz201206042

2012-06-19；

2012-08-01.

天津市科技支撑计划资助项目(10ZCKFGX03600)；国家自然科学基金资助项目(61271322).

闫 格（1983— ），男，博士研究生，eye_ge@163.com.

黄翔东，xdhuang@tju.edu.cn.