电阻层析成像有限元模型优化

肖理庆，王化祥

(1. 天津大学电气与自动化工程学院，天津 300072；2. 徐州工程学院信电工程学院，徐州 221111)

电阻层析成像有限元模型优化

肖理庆1,2，王化祥1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 徐州工程学院信电工程学院，徐州 221111)

为了提高电阻层析成像正问题计算精度，以有限元模型次最外层半径为变量，以敏感场均匀分布时模型均方根值的倒数为适应度函数，利用求解低维多峰值函数优化问题的改进遗传算法，优化模拟敏感场内电流线分布密度与分布形式的新型拓扑结构有限元模型，最后以各峰值点对应的中心流模型均方根值为误差函数，选择新型拓扑结构有限元模型次最外层半径的最优值．仿真实验结果表明，相同实验条件下，相比优化前新型拓扑结构有限元模型、传统按等间隔原理剖分的有限元模型及其改进模型，优化后有限元模型在敏感场均匀分布时模型均方根值分别降低了32.002 5%、83.395 8%和44.760 5%，有效提高了电阻层析成像正问题计算精度与图像重建质量．

电阻层析成像；正问题；有限元模型；遗传算法；图像重建

电学层析成像技术是过程层析成像技术的重要分支，包括电容层析成像(electrical capacitance tomography，ECT)[1-4]、电阻层析成像(electrical resistance tomography，ERT)[5-10]、电阻抗层析成像(electrical impedance tomography，EIT)[11-12]以及电磁层析成像(electromagnetic tomography，EMT)[13-16].由于具有响应速度快、非侵入、价格低廉等优点，电学层析成像技术在医学及工业测量等领域具有广阔的应用前景．

在电学层析成像技术中，有限元模型的拓扑结构对正问题计算精度与图像重建质量具有重要影响．文献[5]以模型每一层半径为变量(最外层除外)，同时将中心区域第1层至第3层半径变量所在区间剖分成多个子区间，分别以有限元平均质量、敏感场均匀分布时模型均方根值的倒数以及两者的乘积为适应度函数，并引入三角形有限元最长边与最短边的比值作为惩罚函数，利用基于区间算法与粒子群算法的改进遗传算法，优化有限元模型拓扑结构，提高了正问题计算精度．但当有限元模型层数较多时，算法存在早熟收敛问题，且模型没有考虑到敏感场内电流线的分布形式；文献[6]模拟敏感场均匀分布时电流线的分布密度与分布形式，设计了一种新型拓扑结构有限元模型，相比传统按等间隔原理剖分的有限元模型及其改进模型，有效提高了电阻层析成像正问题计算精度与图像重建质量，但次最外层半径需人为设置，缺乏理论依据．笔者利用求解低维多峰值函数优化问题的改进遗传算法，对新型拓扑结构有限元模型进行优化，克服了次最外层半径人为设置的主观性与随机性，提高了电阻层析成像正问题计算精度以及对不同流型的反演效果．

1 ERT数学描述

所谓ERT数学模型，即在电流激励条件下，建立敏感场内部区域电导率分布与边界测量电压之间的对应关系．根据恒定电场理论的麦克斯韦方程，ERT传感器敏感场数学模型[5-6]可以描述为

式中：·∇与∇分别为散度及梯度算子；σ为电导率分布；Φ为电势分布函数．

ERT满足第2类边界条件，即

已知被测物场电导率分布σ以及敏感场的边界条件，求取场域内电势分布函数Φ，进而求得边界上各测量电极的电压值即ERT正问题；ERT逆问题是指根据电势分布函数Φ与边界电压测量值，利用图像重建算法求取场域电导率分布σ并以图像的形式表示[6]．

2 基于改进遗传算法的ERT有限元模型优化

以有限元模型次最外层半径为变量，利用求解低维多峰值函数优化问题的改进遗传算法优化新型拓扑结构ERT有限元模型的具体流程如下.

步骤1 设置改进遗传算法种群数目、最大迭代次数、交叉概率、变异概率、学习因子、最大惯性权重、最小惯性权重、莱布尼茨常数等参数．

步骤2 将搜索区间正交分解，利用区间算法将区间分成两类，其中被区间算法排除的区域个体分布密度小，保留下来的区域个体分布密度大，其适应度函数为

式中：x为有限元模型次最外层半径；N为有效边界电压数目；ΦFEM为有限元仿真结果；ΦTheory1为敏感场均匀分布时边界电压理论值，其计算式为

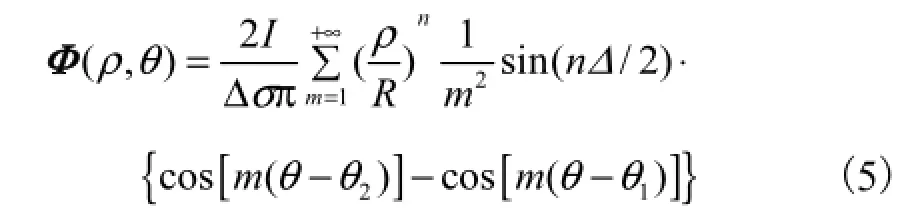
式中：I为激励电流强度；R为场域半径；σ为均匀分布介质的电导率；θ为极角；ρ为极径；Δ为电极所对圆心角；2θ和1θ分别为注入与引出电流电极与坐标轴正实轴所成夹角．

步骤3 按照区域分布密度生成初始种群，并为每个个体赋予表示其所在区域的属性，该属性在算法操作过程中不会发生改变，同时随机产生粒子速度矢量．

步骤4 将种群中每个个体代入式(4)，计算每个个体的适应值并作为评价每个个体优劣程度标准.

步骤5 以每个个体的适应值作为标准，对种群中的每个个体进行选择．本文采取精英策略，即将适应值最小的个体以适应值最大的个体替代，但如果种群中不存在其他与适应值最小的个体属性所表示区域相同的个体，则该适应值最小的个体不被替代，直接进入步骤6．

步骤6 从种群中随机取出个体，根据交叉概率实施交叉操作，形成新的个体．

步骤7 根据变异概率进行变异操作，其计算式为

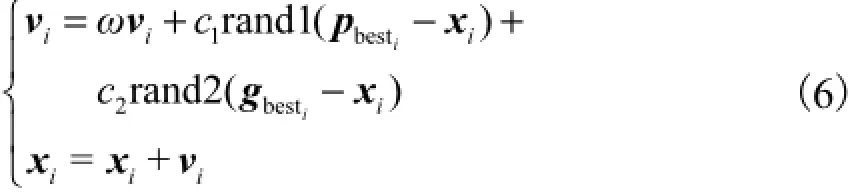
式中：ω称为惯性权重；c1与c2为学习因子，一般取c1=c2=2；rand1与rand2为(0,1)范围里均匀分布的随机数；pbesti与gbesti分别为个体最优值及全局最优值；xi与vi分别为第i个个体的位置与速度矢量．

步骤8 判断运算后种群个体是否在各自属性所表示的区域，若超出区域，则恢复为运算前个体．

步骤9 判断是否满足算法收敛条件．若满足，则将所有峰值点保存并进入步骤10，否则跳转至步骤4，对种群的每个个体进行重新评价并循环计算．

步骤10 以各峰值点对应的中心流模型均方根值为误差函数，选择新型拓扑结构有限元模型次最外层半径的最优值．其函数形式为

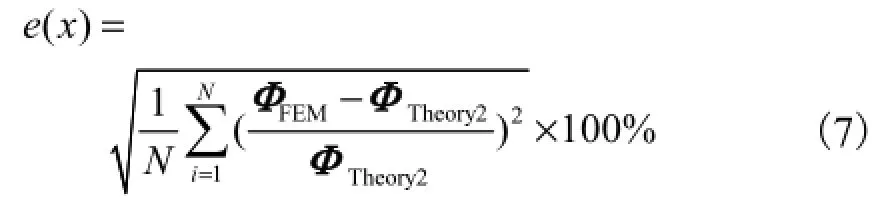
式中ΦTheory2为各峰值点对应的中心流边界电压理论值，其计算式为

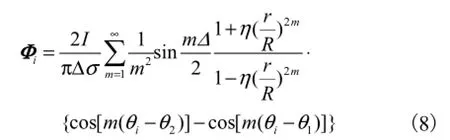
3 仿真实验与分析

3.1 仿真实验条件与算法参数设置

本文仿真实验环境为Pentium M 1.60,GHz CPU、760,M RAM、MATLAB 7.0．改进遗传算法中种群数目为200，最大迭代次数为200，交叉概率为0.80，变异概率为0.01，最大惯性权重为0.9，最小惯性权重为0.01，莱布尼茨常数取1．

3.2 改进遗传算法测试结果

为了测试求解低维多峰值函数优化问题的改进遗传算法性能，现将算法应用于Branin RCOS函数优化，其形式为

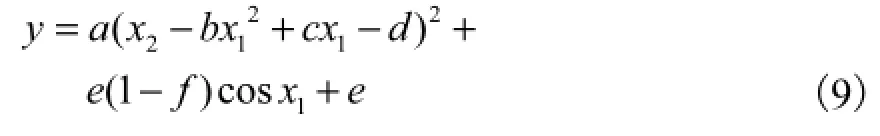
同时，为了获取统计意义的结果，各种不同算法各运行100次，算法测试结果如图1和表1所示[17]．

其中y为算法输出结果的平均值，算法1为本文采用的求解低维多峰值函数优化问题的改进遗传算法，算法2～算法5分别为其他改进遗传算法和粒子群算法，算法6和算法7分别为基本遗传算法与基本粒子群算法，p为概率，情况1与情况2分别表示算法至少收敛到一个最小值点以及收敛到全部最小值点的情况．

图1 不同算法收敛曲线Fig.1 Convergence curves of different algorithms

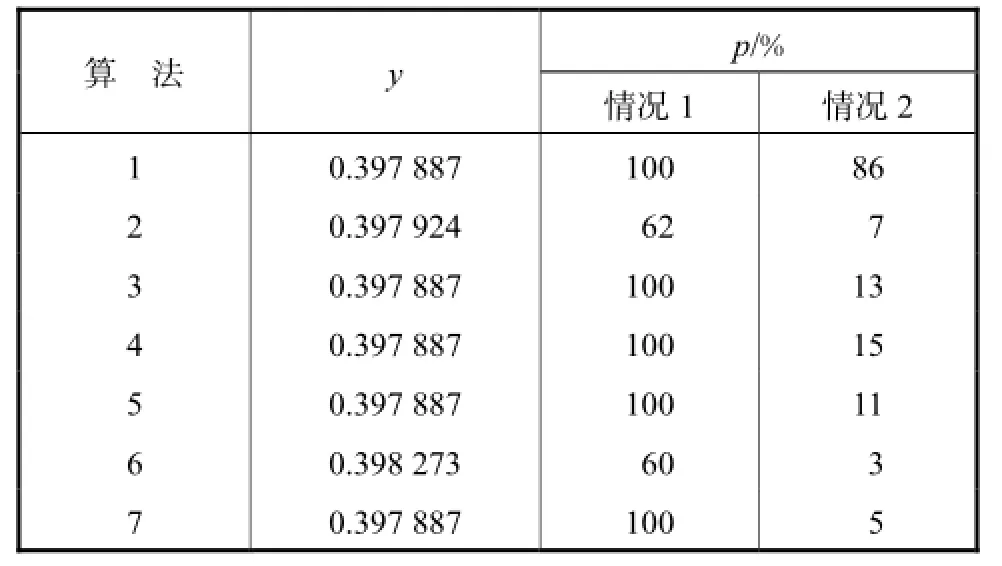
表1 不同算法参数比较Tab.1 Parameter comparison of different algorithms

由图1和表1可知，相同实验条件下，与其他6种算法相比，本文采用的求解低维多峰值函数优化问题的改进遗传算法在不影响算法收敛精度的前提下，可有效提高算法搜索到全部最小值点的概率，具有更强的优化能力．

3.3 ERT有限元模型优化结果

利用求解低维多峰值函数优化问题的改进遗传算法优化后有限元模型如图2模型4所示．

图2 各种有限元模型示意Fig.2 Model sketches of different finite element models

图2中模型1为传统按等间隔原理剖分的有限元模型，模型2为文献[5]提出的改进模型，模型3为文献[6]提出的新型拓扑结构有限元模型．模型1～模型4均包含1,744个有限元、1,017个节点．4种模型在敏感场均匀分布时模型均方根值RMS(即式(4)中F( x)的倒数)分别为6.667%、2.004%、1.628%、1.107%，优化后有限元模型相比其他3种模型，RMS分别降低了83.395,8%、44.760,5%、32.002,5%，有效地提高了电阻层析成像正问题计算精度．

3.4 不同模型图像重建结果

为了验证优化后有限元模型对电阻层析成像重建图像的影响，设置如图3所示8种两相流流型并利用细化后有限元模型(包含7,920个有限元、4,201个节点)获取对应的边界电压，两相流电阻率的比值设置为1∶100，图像重建算法选用修正牛顿-拉夫逊算法，迭代次数设置为400，各种模型重建结果如图4～图7和表2所示．

图3 两相流流型Fig.3 Flow regimes of two-phase flow

其中图像相对误差e的表达式[18]为

式中：g为设置的流型分布；ˆg为重建结果．

图4 模型1重建结果Fig.4 Image reconstruction results of model 1

图5 模型2重建结果Fig.5 Image reconstruction results of model 2

图6 模型3重建结果Fig.6 Image reconstruction results of model 3

图7 模型4重建结果Fig.7 Image reconstruction results of model 4

由图4～图7和表2可知，相同实验条件下，优化后有限元模型有效提高了图像重建质量．4种模型图像相对误差的平均值分别为44.354,0%、23.668,5%、23.237,7%、17.625,1%，优化后有限元模型相比模型1、模型2和模型3分别降低了60.262,7%、25.533,5%、24.153,0%．

考虑到实际中存在不可避免的测量误差，因此，将仿真实验中测量所得的边界电压值加入1.0%幅度噪声，即

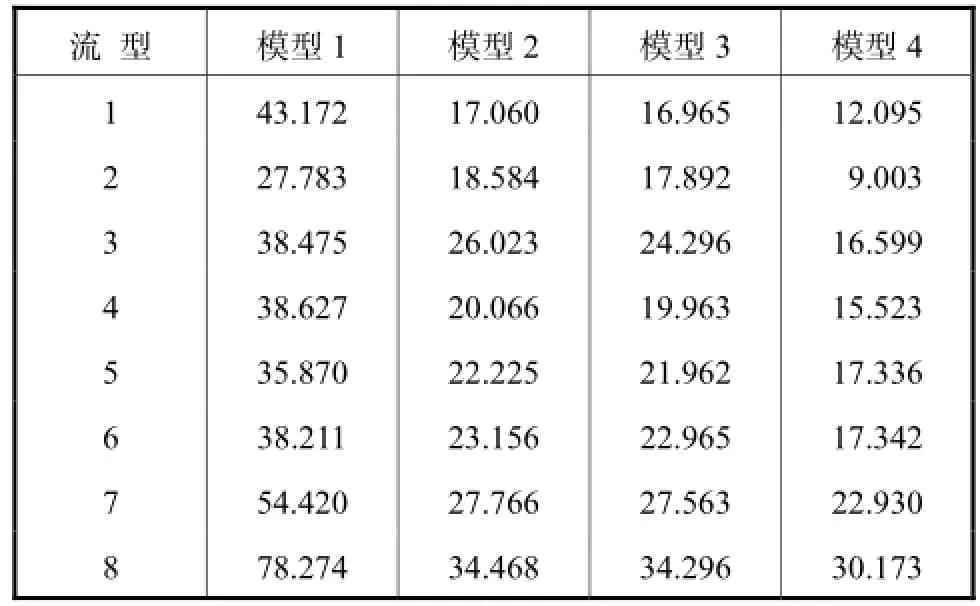
表2 不同模型图像相对误差e比较Tab.2 Comparison of image relative errors ebetweendifferent models %

式中：u为边界电压测量值；f为(1,1)-范围内均匀分布的随机数．

对应的信噪比计算式[6]为

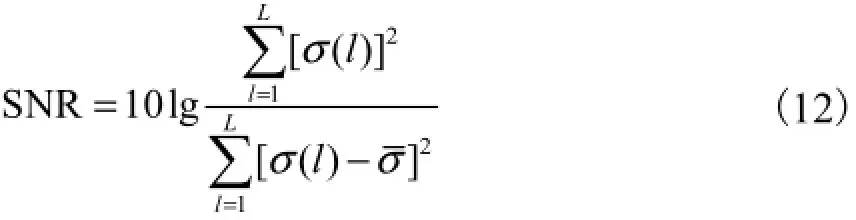
式中σ(l)与σ分别为测量电导率及电导率的平均值.各种模型重建结果如图8～图11和表3所示．

图8 噪声干扰下模型1重建结果Fig.8 Image reconstruction results of model 1 in thepresence of noise

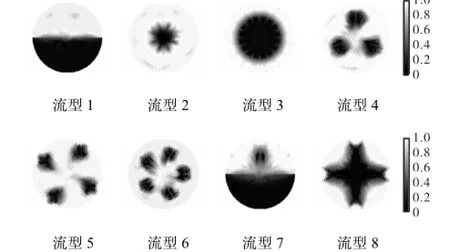
图9 噪声干扰下模型2重建结果Fig.9 Image reconstruction results of model 2 in the presence of noise

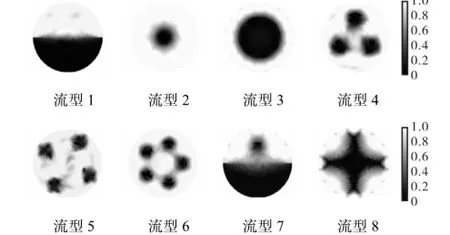
图10 噪声干扰下模型3重建结果Fig.10 Image reconstruction results of model 3 in the presence of noise

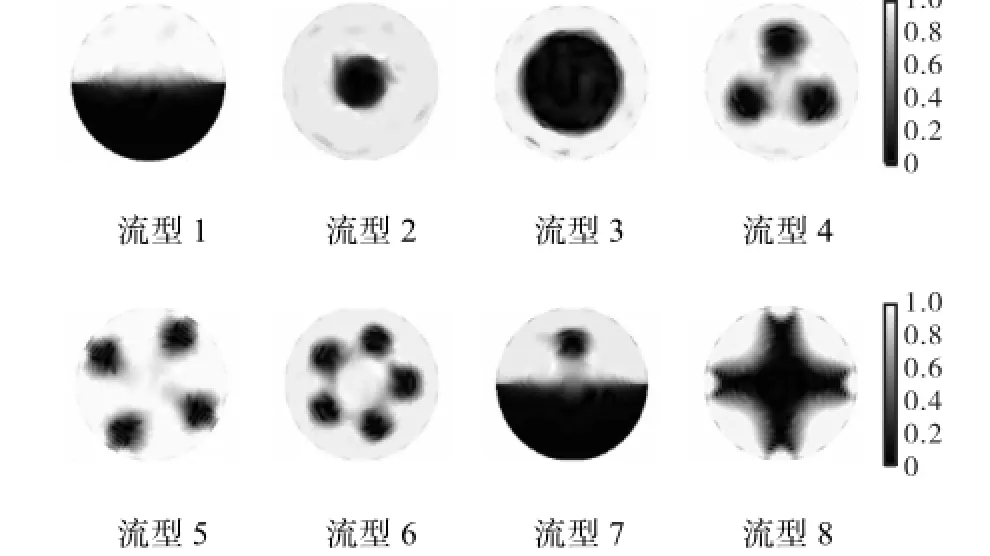
图11 噪声干扰下模型4重建结果Fig.11 Image reconstruction results of model 4 in the presence of noise

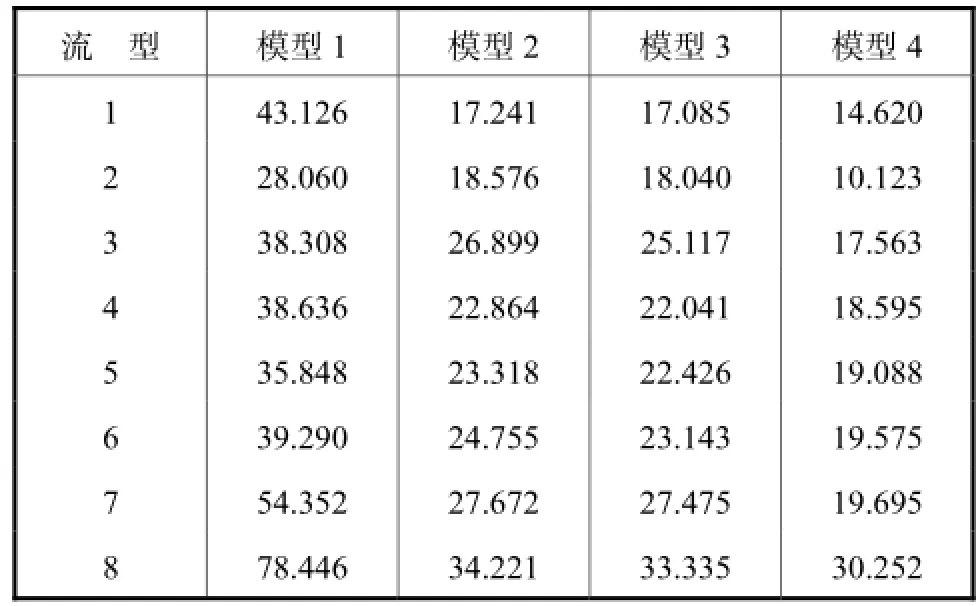
表3 噪声干扰下不同模型图像相对误差e比较Tab.3 Comparison of image relative errors ebetween different models in the presence of noise %

由表3可知，在1.0%幅度噪声干扰下，4种模型图像相对误差的平均值分别为44.508,2%、24.443,2%、23.582,7%和18.688,9%，优化后有限元模型相比模型1、模型2和模型3分别降低了58.010,2%、23.541,5%、20.751,6%．结合图8～图11可知，在1.0%幅度噪声干扰下，优化后有限元模型有效提高了图像重建质量.

4 结 论

为了提高电阻层析成像正问题计算精度与图像重建质量，本文利用求解低维多峰值函数优化问题的改进遗传算法，优化模拟敏感场内电流线分布密度与分布形式的新型拓扑结构ERT有限元模型，仿真实验结果如下．

(1) 优化后有限元模型有效提高了正问题计算精度．相比其他3种有限元模型，优化后有限元模型在敏感场均匀分布时模型均方根值RMS分别降低了83.395,8%、44.760,5%、32.002,5%．

(2) 优化后有限元模型有效提高了图像重建质量．相比其他3种有限元模型，理想情况下，图像相对误差的平均值分别降低了60.262,7%、25.533,5%和24.153,0%；在1.0%幅度噪声干扰下，图像相对误差的平均值分别降低了58.010,2%、23.541,5%和20.751,6%．

［1］ Chen Qi，Liu Shi. Flame imaging in meso-scale porous media burner using electrical capacitance tomography [J]. Chinese Journal of Chemical Engineering，2012，20(2)：329-336.

［2］ 陈德运，陈 宇，王莉莉，等. 基于改进Gauss-Newton的电容层析成像图像重建算法[J]. 电子学报，2009，37(4)：739-743.

Chen Deyun，Chen Yu，Wang Lili，et al. A novel Gauss-Newton image reconstruction algorithm for electrical capacitance tomography system [J]. Acta Electronica Sinica，2009，37(4)：739-743(in Chinese).

［3］ 陈江涛，刘 石. 融合电容层析成像先验信息的集合卡尔曼滤波统计估计[J]. 化学工程，2012，40(4)：36-39.

Chen Jiangtao，Liu Shi. Statistical estimation of ensemble Kalman filter fusion based on priori information approach in electrical capacitance tomography [J]. Chemical Engineering，2012，40(4)：36-39(in Chinese).

［4］ Yang W Q，Beck M S，Byars M. Electrical capacitance tomography-from design to applications [J]. Measurement & Control，1995，28(9)：261-266.

［5］ 肖理庆，王化祥，程红林，等. 改进遗传算法的ERT有限元模型拓扑结构优化[J]. 仪器仪表学报，2012，33(7)：1490-1496.

Xiao Liqing，Wang Huaxiang，Cheng Honglin，et al. Topology optimization of ERT finite element model based on improved GA [J]. Chinese Journal of Scientific Instrument，2012，33(7)：1490-1496(in Chinese).

［6］ 肖理庆，王化祥，韩成春. 一种新型拓扑结构的电阻层析成像有限元模型[J]. 中国电机工程学报，2011，31(20)：100-106.

Xiao Liqing，Wang Huaxiang，Han Chengchun. A new topology structure finite element model of electrical resistance tomography system [J]. Proceedings of the CSEE，2011，31(20)：100-106(in Chinese).

［7］ 张玲玲，王化祥，范文茹. 基于1范数的电阻层析成像图像重建算法[J]. 天津大学学报，2011，44(9)：786-790.

Zhang Lingling，Wang Huaxiang，Fan Wenru. Imagereconstruction algorithm based on 1-norm for electrical resistance tomography [J]. Journal of Tianjin University，2011，44(9)：786-790(in Chinese).

［8］ Daily W，Ramirez A. Electrical resistance tomography [J]. Society of Exploration Geophysicists，2004，23(5)：438-442.

［9］ 李守晓，王化祥，范文茹，等. 基于三维模型的改进正则化ERT成像算法[J]. 天津大学学报，2012，45(3)：215-220.

Li Shouxiao，Wang Huaxiang，Fan Wenru，et al. Improved regularization reconstruction algorithm based on 3D model for ERT system [J]. Journal of Tianjin University，2012，45(3)：215-220(in Chinese).

［10］ Dong Feng，Xu Yanbin. Application of electrical resistance tomography in two-phase flow measurement [J]. Journal of Engineering Thermophysics，2006，27(5)：791-794.

［11］ 王化祥，黄文瑞，范文茹. 三维电阻抗成像的测量模式[J]. 天津大学学报，2012，45(8)：729-734.

Wang Huaxiang，Huang Wenrui，Fan Wenru. Measurement pattern for 3D electrical impedance tomography [J]. Journal of Tianjin University，2012，45(8)：729-734(in Chinese).

［12］ 陈晓艳，张 静. 采用阈值修正法改善电阻抗图像质量[J]. 中国生物医学工程学报，2011，30(4)：481-486.

Chen Xiaoyan，Zhang Jing. Using threshold correction method to improve the image quality of EIT [J]. Chinese Journal of Biomedical Engineering，2011，30(4)：481-486(in Chinese).

［13］ Ma X，Peyton A J，Higson S R，et al. Hardware and software design for an electromagnetic induction tomography(EMT)system for high contrast metal process applications [J]. Measurement Science & Technology，2006，17(1)：111-118.

［14］ 尹武良，王 奔，王化祥. 电磁层析成像中基于半周期采样的数字解调方法[J]. 天津大学学报，2011，44(12)：1118-1123.

Yin Wuliang，Wang Ben，Wang Huaxiang. Digital demodulation based on half-period sampling in electromagnetic tomography [J]. Journal of Tianjin University，2011，44(12)：1118-1123(in Chinese).

［15］ Yin W，Peyton A J. A planar EMT system for the detection of faults on thin metallic plates [J]. Measurement Science & Technology，2006，17(8)：2130-2135.

［16］ 王 超，张军青，徐传进. 基于FPGA的EMT系统设计[J]. 天津大学学报，2011，44(2)：95-100.

Wang Chao，Zhang Junqing，Xu Chuanjin. Design of an electromagnetic tomography(EMT)system based on FPGA [J]. Journal of Tianjin University，2011，44(2)：95-100(in Chinese).

［17］ Xiao Liqing，Wang Huaxiang，Xu Xiaoju. Research on improved genetic algorithm for low-dimension and multimodal function optimization [C]// IEEE Chinese Control and Decision Conference. Mianyang，China，2011：3918-3922.

［18］ Xue Qian，Wang Huaxiang，Cui Ziqiang，et al. Electrical capacitance tomography using an accelerated proximal gradient algorithm [J]. Review of Scientific Instruments，2012，83(4)：1-7.

(责任编辑：孙立华)

Optimization of Finite Element Model for Electrical Resistance Tomography

Xiao Liqing1,2，Wang Huaxiang1
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Department of Information and Electrical Engineering，Xuzhou Institute of Technology，Xuzhou 221111，China)

Aiming to improve the accuracy of solving the forward problem in electrical resistance tomography (ERT)，the new topological finite element model was optimized in this paper. Using the radius of the second outermost layer of the model as a variable，and the reciprocal of the root mean square value of a homogeneous sensitive field distribution as a fitness function，the improved genetic algorithm for solving low-dimension multi-peak function optimization problem was adopted to optimize the new topological finite element model which simulated the current line density and distribution of the sensitive field. Finally，the root mean square value of the core flow model corresponding to each peak point was used as an error function to determine the optimal value of the radius of the second outermost layer of the model. Simulation results demonstrate that，compared to the unoptimized topological finite element model，the conventional finite element model based on uniformly-spaced dissection and its modified version，the optimized model reduce the root mean square value of a homogeneous sensitive field distribution by 32.002 5%，83.395 8% and 44.760 5%，effectively improves both the accuracy of solving the forward problem and the quality of image reconstruction under the same experimental conditions.

electrical resistance tomography；forward problem；finite element model；genetic algorithm；image reconstruction

TK39

A

0493-2137(2014)01-0054-07

10.11784/tdxbz201210020

2012-10-12；

2013-01-08.

国家自然科学基金资助项目(50937005)；徐州市科技计划资助项目(XM12B078)；国家自然科学基金青年科学基金资助项目(61201350，61302122)；江苏省“青蓝工程”资助项目；江苏省高校自然科学研究资助项目(12KJD120002，12KJD510013，13KJD510007).

肖理庆（1981— ），男，博士研究生，讲师，lqx1981@tju.edu.cn.

王化祥，hxwang@tju.edu.cn.