基于矩阵的数据流Top-k频繁项集挖掘算法

尹绍宏，范桂丹

基于矩阵的数据流Top-k频繁项集挖掘算法

尹绍宏，范桂丹

(天津工业大学计算机科学与软件学院，天津 300387)

传统的数据挖掘算法在挖掘频繁项集时会产生大量的冗余项集，影响挖掘效率。为此，提出一种基于矩阵的数据流Top-k频繁项集挖掘算法。引入2个0-1矩阵，即事务矩阵和二项集矩阵。采用事务矩阵表示滑动窗口模型中的事务列表，通过计算每行的支持度得到二项集矩阵。利用二项集矩阵得到候选项集，将事务矩阵中对应的行做逻辑与运算，计算出候选项集的支持度，从而得到Top-k频繁项集。把挖掘的结果存入数据字典中，当用户查询时，能够按支持度降序输出Top-k频繁项集。实验结果表明，该算法在挖掘过程中能避免冗余项集的产生，在保证正确率的前提下具有较高的时间效率。

数据挖掘；数据流；滑动窗口；矩阵；Top-k频繁项集

1 概述

数据流[1]是大量连续到达、随时间不断变化的数据序列，例如超市每天产生的大量售货记录、网页的点击流、通信领域内的电话记录数据流等。数据流产生的数据无法全部保存在内存中，只能按照顺序读取一次或几次[2]。数据流挖掘就是从连续的数据流中提取出潜在有用的信息和知识的过程。对数据流的查询要求实时处理，显然许多传统的数据挖掘算法并不适用于数据流挖掘。数据流挖掘算法要求在单次扫描数据流的前提下获得挖掘结果，并且产生的结果通常是近似结果。

在实际应用中，人们更多地关注近期数据，因此数据流挖掘通常是基于某种特定的时间区间进行的，从而出现了基于窗口的数据流挖掘算法。常用的窗口模型有3种[3]：快照模型，界标模型，滑动窗口模型。应用较多的模型是界标模型和滑动窗口模型。

近来提出了许多数据流频繁项集挖掘算法，典型的有FP-stream算法[4]。此类算法都需要用户指定最小支持度阈值，但面对海量的数据，阈值的设定需要先验知识和一定的专业知识，用户就很难确定合适的阈值。当阈值设置过小时，挖掘出的频繁项集数量非常巨大，会占用大量的内存空间，而挖掘出的结果往往不是用户所需求的；当阈值设置过大时，可能就挖掘出少量的频繁项集。因而让用户指定需要挖掘的个频繁项集，即避免了用户设定最小阈值，又使挖掘更具有针对性。

对于Top-k频繁项集的挖掘，学者们提出了许多算法。文献[5]提出了Itemset-Loop算法，此算法在Apriori算法[6]的基础上进行了改进，能够挖掘出静态数据库中的Top-k频繁项集，但是此算法不支持数据的增量更新。文献[7]研究了数据流最频繁的个项的挖掘算法，但是并没有涉及多项集的处理问题。

本文提出一种基于矩阵的数据流Top-k频繁项集挖掘算法TKFM，该算法引入2个0-1矩阵，一个是事务矩阵，存储事务中各项的相关信息；另一个是二项集矩阵，存储2-项集的信息。通过2个矩阵的相关操作，将挖掘出的频繁项集存储到数据字典中来实现数据流中前个频繁项集的挖掘。

2 基本概念

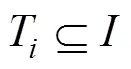
定义2滑动窗口的起始点与终止点都没有明确的界限[8]，的终止点为当前时刻。其中，的大小为窗口中所包含的事务数目，由用户预先定义。每当有一个新的事务到达窗口，窗口就滑动一次。新的事务不断进入窗口，旧的事务相继被删除，滑动窗口不断被更新。

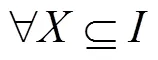
定义4 Top-k频繁项集。将数据流中的所有项集按照支持度降序排列，设排在第位项集的支持度为border- sup，则中所有支持度不小于border-sup的项集的集合即Top-k频繁项集。

假定文中所有的项都是按照全序关系排列的。

3 TKFM原理与算法

3.1 算法所用数据结构

3.1.1 事务矩阵

行表示数据流中项的集合={1,2,…,I}，列表示依次到达的事务{1,2,…,T}。设滑动窗口的大小为||=(即矩阵的列数)，项集中共有个项，则建立一个(+1)×的事务矩阵，并将矩阵中的每个元素初始化为0，其中第(+1)行为count行。扫描依次到达的数据流，若窗口未满，则将依次到来的事务T加入到矩阵中，其中，若项目在 第条事务中出现，则将A置1，否则置0；若窗口已满，则需先删除窗口中最旧的事务，然后再添加新的事务。设当前到达的事务为T，最旧事务所在列为column，则最旧事务所在的列column为%。count记录每列中1的个数，即事务的长度。

3.1.2 数据字典Dictionary

记录当前数据流中的项集及其支持度，且支持度按降序排列。Dictionary中的每一个项都是一个二元组，其中，sup表示项在当前数据流中的支持度；item表示项。Dictionary的内部结构如图1所示。

图1 Dictionary的内部结构

对于Dictionary中的每个项，支持度sup是关键字，在整个数据字典中是唯一的，不允许重复，且一个sup可以对应多个item。其中，存储某个sup对应的item时，需要在磁盘中占用一片连续的区域。

对数据字典进行访问是通过关键字sup进行的。当需要访问某个sup的item集合时，首先要找出关键字sup，然后通过关键字找到对应的item集合，按照顺序读取出对应元素。

3.1.3 二项集矩阵

3.2 TKFM算法的基本原理

以表1所示的事务数据流为例，介绍TKFM算法的基本思想，设=2，||=5。

表1 事务数据流

3.2.1 窗口初始阶段

当窗口内的事务数小于||时，处于窗口初始阶段。在此阶段，新的事务不断进入窗口，直到窗口满为止。则表1中的事务数据流的事务矩阵如表2所示。

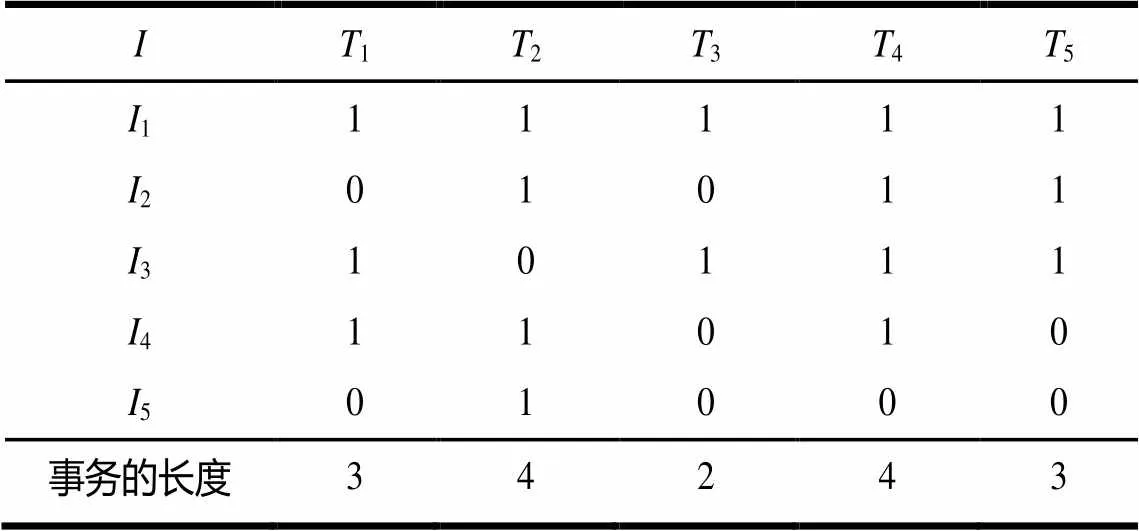
表2 窗口初始阶段的事务矩阵A

3.2.2 窗口滑动阶段

当窗口满时，处于滑动窗口阶段。在此阶段，最旧的事务1被删除，新到来的事务6添加到滑动窗口中，则 表2中的事务矩阵更新为表3。

表3 滑动窗口阶段的事务矩阵A

3.2.3 Top-k频繁项集产生阶段

Top-k频繁项集产生的过程如下：

(1)计算表3中事务矩阵每行中1的个数，即每个项的支持度，然后将二元组存入Dictionary中，并按支持度降序排列，找出第2个项的支持度，此时border-sup为2，然后删除支持度小于border-sup的项，即完成top-2频繁一项集的寻找。

(2)根据Dictionary中的频繁一项集构造二项集矩阵。在构造矩阵的同时，将支持度大于等于border-sup的2-项集存入2中，同时将二元组存入Dictionary中，并按支持度降序排列，找出第个项集的支持度，更新border-sup为3，并删除支持度小于border-sup的项。二项集矩阵如表4所示。

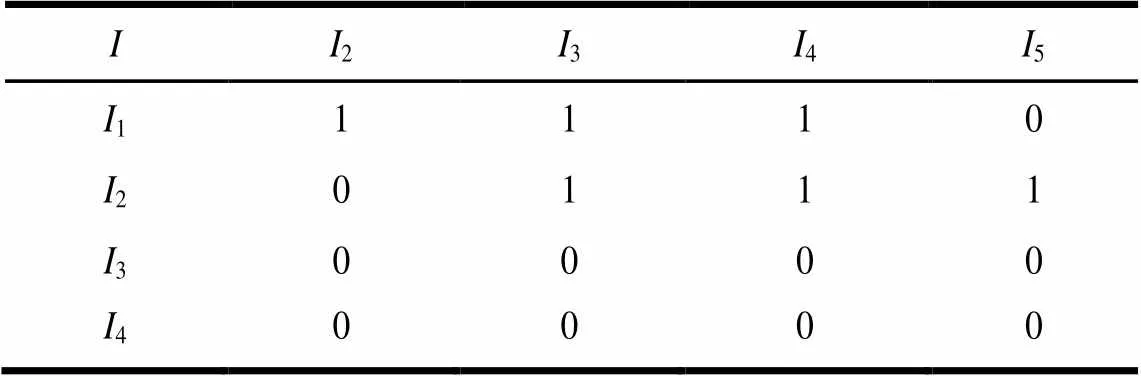
表4 二项集矩阵B

(3)根据C中的项和中的信息，可以将频繁2-项集扩展到3-项集{{1,2,3}、{1,2,4}}，再将事务矩阵中的各相关行做逻辑与运算，将支持度大于等于border-sup的二元组存入Dictionary中。本例中的3项集不满足条件，算法 结束。

此例得到的top-2频繁项集如图2所示。

图2 top-2频繁项集

3.3 TKFM算法描述

根据上述分析，算法包括3个关键步骤：窗口初始阶段，滑动窗口阶段，Top-k频繁项集产生阶段。下面给出算法的伪代码。

输入数据流，用户指定的，滑动窗口的大小||

输出Top-k频繁项集

(1)滑动窗口中的每个事务Tj

if(W is not full)//窗口初始阶段

{

for(i=1;i<=m;i++)

if(Iiin Tj)

A[i,j]=1;

else A[i,j]=0;

}

(2)else//窗口滑动阶段

int column=j%w;

更新矩阵A中第column列的值，其余列保持不变

(3)扫描A中的前m行，将二元组存入Dictionary中，并按支持度降序排列。若Dictionary中的项小于k，则初始化border-sup=0，否则border-sup为第k个项的支持度，删除支持度小于border-sup的二元组

(4)根据Dictionary中的一项集构造二项集矩阵B，产生候选二项集C2，同时将支持度大于等于border-sup的二元组存入Dictionary中，并按支持度降序排列，找出第k个项的支持度，更新border-sup，并删除支持度小于border-sup的二元组

(5)//Top-k频繁项集产生阶段，Ck={Ii1,Ii2,…,Ii(k-1)}是频繁//(k-1)-项集

If(B[i(k-1),iu]=1)and(B[i1,iu]=B[i2,iu]=B[i(k-2),iu]=1)

{

扩展为k-项集{Ii1,Ii2,…, Ii(k-1),Iu}

if(sup({Ii1,Ii2,…, Ii(k-1),Iu})>=border-sup)

Lk={Ii1,Ii2,…, Ii(k-1),Iu};

将存入Dictionary中

}

(6)将Dictionary中的项统一按支持度降序排列，找出第k个项的支持度，更新border-sup，并删除支持度小于border-sup的二元组

(7)重复步骤(5)和步骤(6)，直至不产生更大的项集为止

(8)输出Top-k频繁项集

4 实验结果与分析

本文算法采用IBM data generator[11]生成的模拟数据，算法的实现语言是C#，其开发工具是Visual Studio 2010，算法的运行环境为Windows XP操作系统，Intel core 3.30 GHz CPU，3 062 MB内存。算法采用的数据集是稀疏集T10I4D100K和稠密集T40I10D100K，其中，T表示事务的平均长度；I表示前项频繁项集的平均长度；D表示数据流中事物的总数。实验所用的2个数据集由10万条事务组成，前项频繁项集的平均长度分别为4和10。设定滑动窗口||=10 000。

设定=100，在2个数据集上测试算法的性能，结果如图3所示。从图中可以得到，随着处理的事务数的不断增大，算法所花费的时间呈近似线性增长的趋势，在T40I10D100k数据集上所花费的时间增长较快，原因是此数据集中项的平均长度较长，在窗口滑动及更新时需花费较长时间，且在挖掘Top-k频繁项集时也需较长时间。

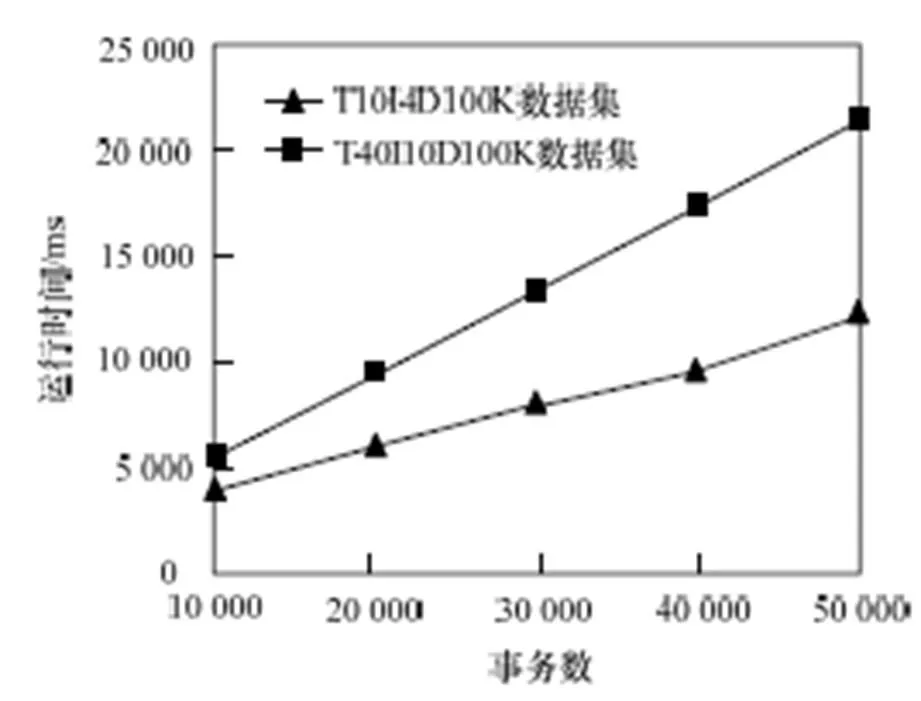
图3 不同数据集上本文算法的运行时间

图4通过设置不同的值，测试值对算法性能的影响。在稀疏集T10I4D100k上分别测试了4个不同的值，从图中可以看到，随着事务数的不断增加，每个值所花费的时间呈平稳增长的趋势。在处理相同事务数的情况下，值越大，挖掘所花费的时间越长，这是因为值越大，更新、查找、插入和排序更多的频繁项集需要较长的时间。

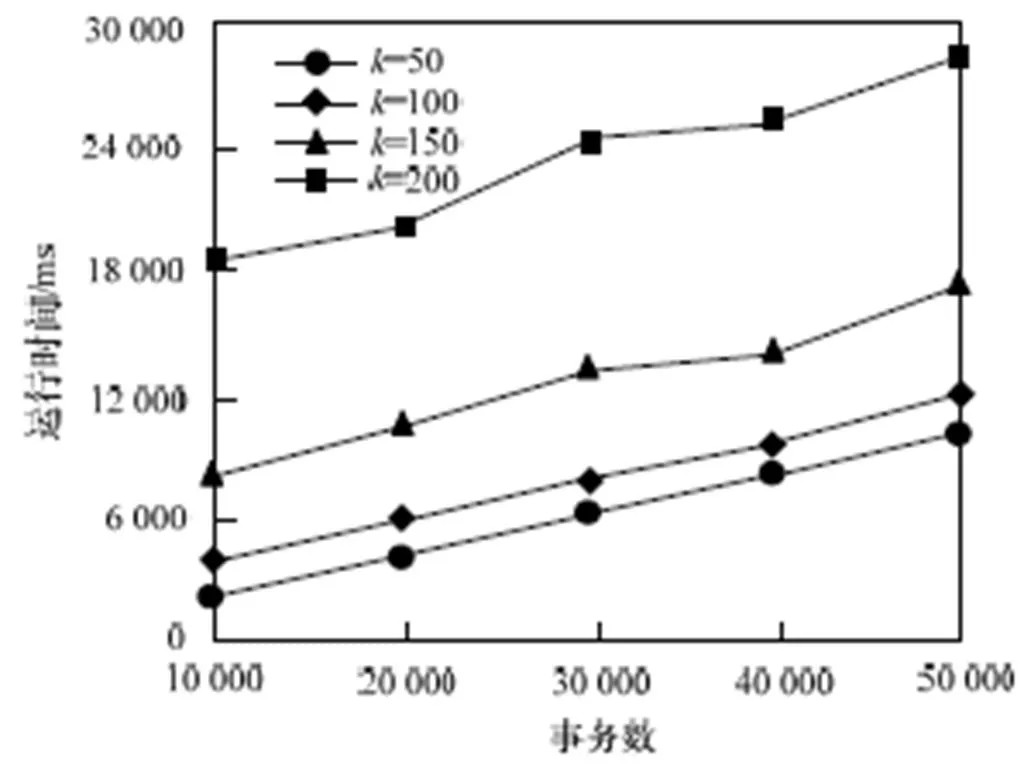
图4 不同k值下本文算法的运行时间

实验对TKFM算法和MTKFI[12]算法进行了比较。MTKFI算法是利用位图存储事务的相关信息，在Top-k频繁项集挖掘阶段，算法利用类Apriori的思想产生Top-k频繁项集，并把挖掘的结果存储在二层索引链表中。此算法在Top-k频繁项集产生的过程中，需要不断地进行连接和剪枝操作，会产生大量的冗余项集，因而算法的时间效率不高。TKFM算法在Top-k频繁项集产生的过程中，省去了连接和剪枝操作，从而避免产生大量冗余项集，提高了挖掘的时间效率。在挖掘5万条事务的前提下，使用稠密集T40I10D100k进行实验，TKFM算法和MTKFI算法在不同值下的运行时间如图5所示。通过实验可以看出，随着值的增大，本文算法的时间效率提高得越明显。

图5 不同k值下2种算法的运行时间比较

5 结束语

本文提出了一种基于矩阵的数据流Top-k频繁项集挖掘算法，利用滑动窗口对数据流进行逐条采样，并用2个0-1矩阵存储相关信息，通过逻辑与运算计算候选项的支持度。理论分析和实验结果均表明，该算法能够挖掘出Top-k频繁项集，且与MTKFI算法相比，其时间效率更高。如何减少算法的内存消耗是下一步要研究的问题。

[1] Babcock B, Babu S, Datar M, et al. Models and Issues in Data Stream Systems[C]//Proc. of the 21st ACM SIGMOD- SIGART Symposium on Principles of Database System. New York, USA: ACM Press, 2002: 1-16.

[2] 王 磊, 黄志球, 朱小栋, 等. 数据流中基于矩阵的频繁项集挖掘[J]. 计算机科学与探索, 2008, 2(3): 330-335.

[3] 孙玉芬, 卢炎生. 流数据挖掘综述[J]. 计算机科学, 2007, 34(1): 1-5.

[4] Giannella C, Han Jiawei, Pei Jian, et al. Mining Frequent Patterns in Data Streams at Multiple Time Granularities[M]. Cambridge, USA: MIT Press, 2005.

[5] Fu A W, Kwong R W, Renfrew F. Mining N-most Interesting Itemsets[C]//Proc. of International Symposium on Methodo- logies for Intelligent Systems. Charlotte, USA: [s. n.], 2000: 59-67.

[6] Agrawal R, Srikant R. Fast Algorithms for Mining Association Rules[C]//Proc. of the 20th International Conference on Very Large Data Bases. Santiago, Chile: [s. n.], 1994.

[7] Metwally A. Efficient Computation of Frequent and Top-k Elements in Data Streams[C]//Proc. of International Conference on Database Theory. Edinburgh, UK: [s. n.], 2005: 398-412.

[8] Li Huafu, Lee S Y. Mining Frequent Itemsets over Data Streams Using Efficient Window Sliding Techniques[J]. Expert Systems with Applications, 2008, 33(2): 286-298.

[9] 韩家炜. 数据挖掘概念与技术[M]. 北京: 机械工业出版社, 2007.

[10] 徐嘉莉, 陈 佳. 基于向量的数据流滑动窗口中最大频繁项集挖掘[J]. 计算机应用研究, 2012, 29(3): 837-840.

[11] Agrawal R, Srikant R. Fast Algorithms for Mining Association Rules[C]//Proc. of the 20th International Conference on Very Large Database. San Francisco, USA: Morgan Kaufmann Publishers, 1994: 487-499.

[12] 刘立新. 数据流频繁模式挖掘算法研究[D]. 长沙: 中南大学, 2010.

编辑 任吉慧

Top-k Frequent Itemsets Mining Algorithm over Data Streams Based on Matrix

YIN Shao-hong, FAN Gui-dan

(School of Computer Science and Software Engineering, Tianjin Polytechnic University, Tianjin 300387, China)

The past algorithms produce large amounts of redundant itemsets, and they affect the efficiency of data mining. Therefore, a Top-k frequent itemsets mining algorithm over data streams based on matrix is proposed. Two 0-1 matrices, transaction matrix and 2-itemsets matrix, are introduced into the algorithm.Using transaction matrix to express the transaction list of a sliding window, and 2-itemsets matrix is obtained by calculating the support of each row. Thenit can get candidate items by 2-itemsets matrix, and Top-k frequent itemsets are obtained by calculating the support of candidate items through logic and operation of correspond row in transaction matrix. Finally it saves the result of data mining into data dictionary.The algorithm can output the Top-k frequent itemsets by support in descendant order when user queries. Experimental results show that the algorithm avoids redundant itemsets in the process of data mining, and the efficiency of data mining is improved appreciably under the premise of accuracy.

data mining; data stream; sliding window; matrix; Top-k frequent itemset

1000-3428(2014)03-0055-04

A

TP311.13

尹绍宏(1964－)，女，副教授，主研方向：数据挖掘；范桂丹，硕士研究生。

2013-01-11

2013-03-10 E-mail：yinsh@tjpu.enu.cn

10.3969/j.issn.1000-3428.2014.03.011