基于广义改进型Hammerstein模型的宽带射频功率放大器建模
许高明 刘太君 叶 焱 文化锋 李 军
基于广义改进型Hammerstein模型的宽带射频功率放大器建模
许高明 刘太君*叶 焱 文化锋 李 军
(宁波大学信息科学与工程学院 宁波 315211)
为了提高AH模型的建模精度,该文在AH模型的带记忆弱非线性模块中引入滞后包络项和超前包络项,用于仿真功率放大器的滞后包络效应和超前包络效应,从而构建出广义改进型Hammerstein模型(GAH)。通过实验比较了GAH模型和AH、记忆多项式、分数阶记忆多项式以及广义记忆多项式模型的建模精度和模型复杂度。实验结果显示GAH模型能在很低的计算复杂度下很好地表征功率放大器的记忆效应。
无线通信;射频功率放大器;功率放大器建模;Hammerstein模型;4G;记忆效应
1 引言
近年来,随着无线通信的迅猛发展,数字预失真技术成为3G和4G移动通信系统中被广泛采用的线性化技术。应用于数字预失真技术的典型功率放大器的行为模型有查找表(Look Up Table, LUT)模型[1]、Volterra 级数[2,3]模型、人工神经网络[4,5]模型、记忆多项式[6,7](Memory Polynomial, MP)模型、分数阶记忆多项式模型[8](Fractional-order Memory Polynomial, FMP)、广义记忆多项式模型[9,10](Generalized Memory Polynomial, GMP), Hammerstein模型[11], Wiener模型[11]、改进型Hammerstein (Augmented Hammerstein, AH) 模型[12,13]等。在这些行为模型中,基于Hammerstein和Wiener的两厢式模型具有实现复杂度低、数值稳定性好等优点,因此被广泛应用于构建带记忆效应的射频功率放大器模型。而在两厢式行为模型中,AH模型可以更准确地对3G移动通信系统的射频功率放大器进行建模。但是,由于4G移动通信系统的宽带射频功率放大器中存在严重的记忆效应,因此AH模型的建模能力无法满足对4G功率放大5器进行精确建模的需要。本文在AH模型的带记忆弱非线性模块中引入滞后包络项和超前包络项,从而构建了一种广义改进型Hammerstein模型(Generalized Augmented Hammerstein, GAH)。该模型的结构与改进型Hammerstein模型类似,均采用无记忆强非线性模块串联带记忆弱非线性模块的两厢式架构,其中无记忆强非线性模块用于仿真功率放大器的静态非线性,带记忆弱非线性模块用于仿真功率放大器的记忆效应。
本文将首先论述提出的GAH模型;然后讨论GAH模型参数的求解方法;在此基础上,利用实验验证平台提取的被测射频功率放大器的等效基带输入输出信号,对功率放大器进行非线性建模和实验验证。
2 广义改进型Hammerstein(GAH)模型
2.1 广义改进型Hammerstein(GAH)模型
为了发掘AH模型对宽带射频功率放大器记忆效应仿真的潜力,本文对AH模型的包络项进行了扩展。AH模型的输入输出关系可以简化表示为
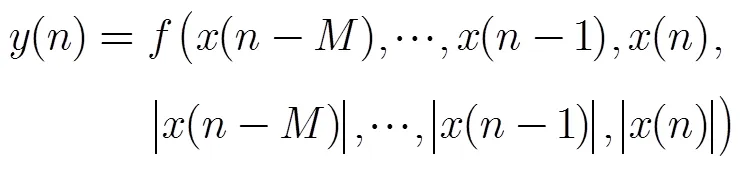
其中,()和()分别为模型的输入输出信号;为记忆深度。从式(1)可以看出,模型的输出信号由当前时刻的输入信号和前时刻的输入信号决定。
将AH模型包络项的输入信号向左右各平移c和d个时钟,此时新模型的输出为
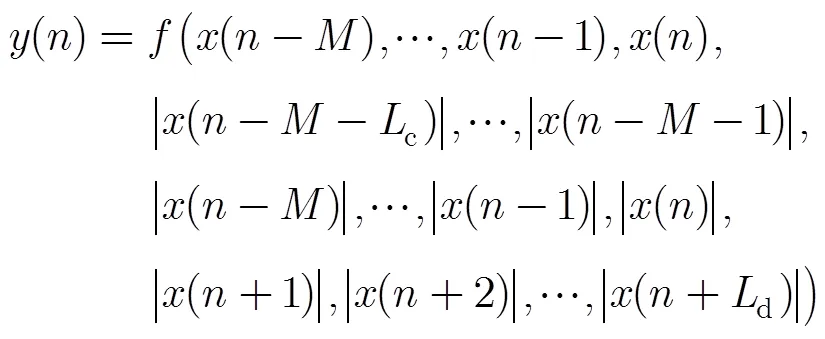
其中c,d分别为滞后包络和超前包络延时长度。与式(1)相比,式(2)中,模型的输入包络信号在数学上更具有完备性。式(2)增加了滞后于传统记忆深度的包络信号,同时引入了超前于现在时刻的包络信号,这使得模型的输入包络信号更加完整,从而能够更完整地表征由功率放大器偏置电路引起的记忆效应。
基于以上分析,本文在AH模型的带记忆弱非线性模块中引入滞后包络项和超前包络项,从而构建出广义改进型Hammerstein模型。GAH模型的无记忆强非线性模块用来仿真射频功率放大器的静态强非线性特征;带记忆弱非线性模块则借用有限长单位冲激响应(Finite Impulse Response, FIR)滤波器网络实现对射频功率放大器记忆效应的仿真。该模型的数学表达式如(3)所示:

2.2 GAH模型参数辨识
GAH模型的参数识别分两步进行。第1步先求出无记忆强非线性模块的参数,即求解多项式的系数。第2步将去除静态非线性后的信号样本序列作为输入序列,进行带记忆弱非线性模块系数的求解。在进行多项式求解时,多项式的输入输出为测量得到的功率放大器输入输出样本。数学表达式为
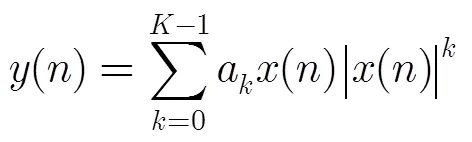
式中()和()分别为功率放大器的输入输出信号;为多项式阶数。
根据功率放大器的输入输出特性,本文设定多项式的阶数=9。求解GAH模型无记忆强非线性模块时,首先采用奇异值分解 (Singular Value Decomposition, SVD)算法求解多项式,然后将计算的系数代入多项式并去除静态非线性,最后将多项式输出信号作为带记忆弱非线性模块的输入进行第2步求解。
由于GAH模型的带记忆弱非线性模块中含有超前包络项,因此在模型实现时需要对输出信号进行相应的延时。此时带记忆弱非线性模块数学表达式如式(5)所示。
式(5)可以采用文献[12]和文献[14]提出的方法将非线性方程转换成线性方程,从而通过SVD算法求解线性方程组的方式来提取GAH模型的带记忆弱非线性模块参数。
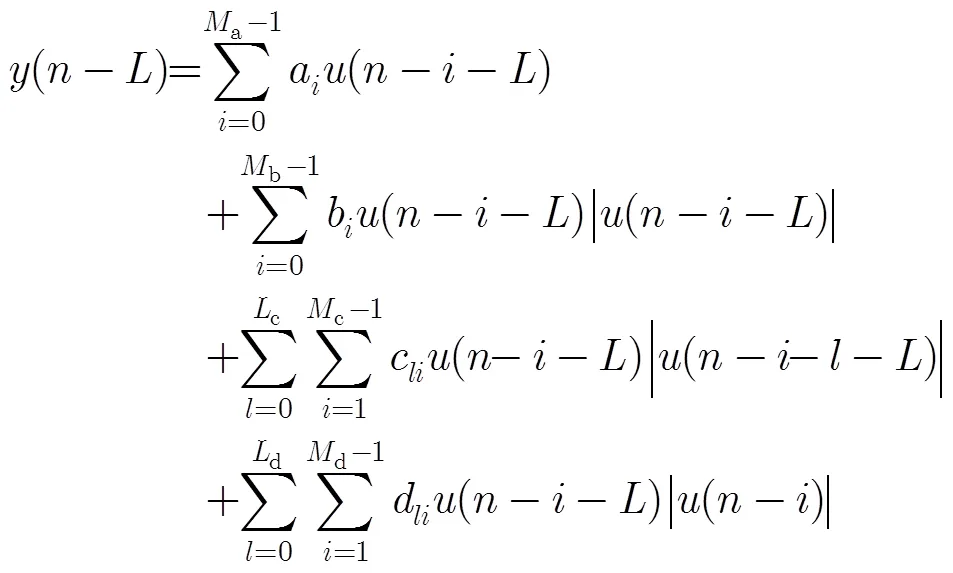
3 模型的实验验证
3.1实验验证平台

此外,平台测试信号为带宽20MHz单载波FDD-LTE信号,该测试信号峰均值功率比(Peak to Average Power Ratio, PAPR)为8.7 dB。被测宽带射频功率放大器为中心频率为1960 MHz,带宽40 MHz,输出功率45 dBm的Doherty功率放大器。功率放大器芯片为NXP公司的LDMMOS对管BLF7G20L-90P。
3.2 模型比较
为了验证GAH模型建模精度和计算复杂度,本文采用归一化均方误差(Normalized Mean Square Error, NMSE)和浮点运算数(FLoating point OPerations, FLOPs)对GAH, AH, MP, FMP和GMP模型进行了比较,比较结果如图1和图2所示。这里设定AH模型记忆深度= Max(1,2); GMP模型记忆深度=Max(a,b,c),阶数=Max(a,b,c),滞后超前包络延时= Max(b,c); GAH模型记忆深度= Max(a,b,c,d),滞后超前包络延时=Max(c,d)。
图1中AH模型和GAH模型的阶数均为9阶;GAH模型滞后/超前包络项选取的延时长度分别为1, 4和6, GMP模型的滞后/超前包络效应延时长度分别为1和2,阶数为5阶。MP和FMP模型的阶数均为10阶。从图1可以看出,AH模型NMSE收敛于-41.5 dB, MP和FMP模型的NMSE收敛于-42.6 dB; GAH模型随着滞后/超前包络项延时长度的增加,NMSE逐渐收敛。GAH滞后/超前包络项延时长度为1和6时,NMSE分别收敛于-43.4 dB和-44.0 dB;滞后/超前包络项延时长度为1和2的5阶GMP模型的NMSE分别收敛于-44.2 dB和-44.5 dB。通过比较可以看出GAH模型的NMSE即使在滞后/超前包络项延时长度为1时,也比AH模型低2 dB左右,比MP和FMP模型低1 dB左右;与GMP模型比较,GAH模型的NMSE略高,但在相同NMSE条件下,GAH模型具有更低的计算复杂度。
图2引入FLOPs来表达不同计算复杂度下各模型的NMSE结果。图中AH模型和GAH模型的阶数均为9阶;AH, MP, FMP和GAH模型的记忆深度的值为1到12; GMP模型的记忆深度为1到5;GAH模型的滞后/超前包络项选取的延时长度分别为1, 4和6; GMP模型的滞后/超前包络效应延时长度分别为1和2,阶数均为5阶;MP和FMP模型的阶数均为10阶。从图上可以看出,AH模型Flops最少,但NMSE最高;FMP模型的NMSE略好于MP模型,但FLOPs要多于MP模型;GAH模型随着滞后/超前包络项延时长度的增加,FLOPs增多明显。但是在相同NMSE条件下,GAH模型的FLOPs要比MP, FMP和GMP模型少得多。如NMSE在-43 dB时,GAH模型的滞后/超前包络项延时长度只需为1即可达到。此时GAH模型的FLOPs为390,而GMP模型的FLOPs高达845,超过GAH模型的两倍。当NMSE在-44 dB时,GAH模型的FLOPs为1950,而GMP模型的FLOPs则高达2600。通过以上的比较可以看出GAH模型具有建模精度高,计算复杂度低的优点。当然,GAH的建模精度相比GMP模型还存在一定差距,不过低计算复杂度是它的主要优势。
为了更好地比较几种模型,本文还采用了文献[14]和文献[15]提供的测量射频功率放大器记忆效应的方法对比几种模型仿真由记忆效应主导的残余频谱再生的能力。该方法如图3所示,在被测功率放大器和功率放大器模型输入前端插入无记忆LUT预失真器,对它们进行预失真线性化处理。无记忆LUT预失真器去除了功率放大器和行为模型的静态强非线性,从而能够更加清晰地显示各模型对于记忆效应的仿真效果。经过LUT预失真器线性化后的功率放大器和行为模型的残余频谱再生如图4所示。此时各模型的参数设置如表1所示。从图4可以看出,GAH模型的残余频谱再生最接近功率放大器的实际测量值,其次是GMP 模型;MP和FMP两种模型的残余频谱再生非常相近,但与功率放大器实际测量的残余频谱再生存在一定差距。AH模型产生的残余频谱再生比MP和FMP模型产生的要更差一些。与功率放大器实际测量的残余频谱再生差别最明显的是LUT模型,因其不具有记忆效应仿真功能。为了使各个模型产生的残余频谱再生易于辨认,图5对图4的残余频谱再生部分进行了局部放大。

图1 不同记忆深度下NMSE的变化

