沙坝海岸沿岸流速度剖面特征研究

王彦，邹志利

（1.大连理工大学海岸及近海工程国家重点实验室，辽宁大连 116024）

沙坝海岸沿岸流速度剖面特征研究

王彦1，邹志利1

（1.大连理工大学海岸及近海工程国家重点实验室，辽宁大连 116024）

通过对两个坡度沙坝地形沿岸流实验测量和基于能量方程的沿岸流数值模拟，研究了沙坝海岸平均沿岸流速度剖面的双峰剖面特征，重点分析了第二个峰值的特征和两峰值的比值。综合考虑入射波高、入射波类型和坡度对波生沿岸流垂直岸线速度剖面的影响。结果表明，平均沿岸流速度剖面出现双峰剖面特征：第一峰值发生在沙坝向岸侧面的中部，第二个峰值发生在靠近岸线处；同一坡度情况两个峰值的位置和比值，不受入射波类型、入射波高的影响。数值模型中包括了侧混、底摩擦和水滚等因素，其数值模拟结果和实验值拟合较好，并讨论了有无侧混和水滚对速度剖面的影响。

双峰剖面；二峰值；波浪破碎；沙坝

1 引言

波浪斜向传入海岸时，在沙坝上由于水深较浅将发生破碎，导致波高衰减，并会在破波带内产生平行于岸线的流动——沿岸流。沿岸流的范围和强度对于研究海岸变形以及近岸水域污染物输移扩散规律都有重大意义。

目前对沿岸流的现场观测和模型实验研究已有近半个世纪的历史。Ruessink等［1］和Feddersen等［2］认为沿岸流速度最大值发生在波浪破碎最强烈位置。对于平坡海岸，波浪传播至浅水区域只发生一次破碎，速度剖面只有一个峰值。通过对现场观测结果［3—4］和实验室模型试验结果［5—6］的比较，在平底海滩下两者的波生沿岸流速度剖面结果符合较好。对于沙坝海岸，沙坝的存在导致波浪在沙坝上发生一次破碎，在沙坝向岸侧沟槽又恢复不破碎状态并继续向岸传播，波浪通过沙坝折射后剩余的能量在靠近岸线处再次耗散而发生二次破碎，波浪的两次破碎使得在沙坝海岸沿岸流速度剖面出现双峰值剖面特征。对于沙坝海岸沿岸流速度剖面最大值位置存在不同观点，Birkemeier［7］、Feddersen等［2］及Kuriyama和Nakatsukasa［8］通过对DELILAH的现场观测实验发现：在天然沙坝地形的沿岸流速度剖面的最大值出现在沙坝沟槽里。Reniers和Battjes［9］把Visser提出的水泵循环系统应用到沿岸流的物理模型实验，并建立了一个考虑水滚作用的沿岸流模型。通过EMF流速仪定量测量出沿岸流速度最大值发生在沙坝顶，由于测量流速的EMF受到最小水深的限制，并没有测量出岸线附近的沿岸流速度第二峰值，仅通过投入染料的方法定性地观测到在岸线附近出现速度第二峰值。Hamilton和Ebersole［10］将水泵循环系统应用到大尺度泥沙输移实验，用来建立沿岸分布均匀的沿岸流，通过控制20个独立水泵的泵水量建立双循环系统。邹志利等［11—12］进行了平坡海岸沿岸流实验研究，并建立了基于能量方程的时均沿岸流模型，讨论不同涡粘系数对沿岸流速度剖面的影响。孙涛等［13］建立了基于高阶抛物化缓坡方程的波生沿岸流模型，并和平坡海岸沿岸流实验结果吻合较好，发现波生沿岸流速最大值出现的位置并不是与波浪破碎线重合，其位置稍落后于波浪破碎线位置。Zheng和Tang［14］建立了关于沿岸流最大值与破波点的空间滞后现象的准三维近岸流模型，认为水滚将使沿岸流峰值向岸移动，从而滞后于破波点位置。解鸣晓和张玮［15］建立了综合考虑辐射应力垂向分布、水滚、波浪水平和垂向湍流混合系数的三维近岸流模型。房克照等［16］建立了基于二阶完全非线性Boussinesq水波方程的时域沿岸流数值模型，并针对均匀坡度海岸上沿岸流进行数值模拟。

本文通过对坡度分别为1∶40和1∶100两种沙坝海岸上的沿岸流进行实验测量，研究沙坝地形沿岸流的双峰速度剖面特征，特别是第二个峰值的特征。分别讨论了波高、入射波类型和坡度的变化对平均沿岸流速度剖面的影响。因为没有采用泵循环系统，本文试验中对沿岸方向沿岸流的均匀性也进行了细致的考察。建立了基于波能守恒方程的沿岸流数值模型，考虑侧混、底摩擦和水滚的影响，对波高、波浪增减水和沿岸流速度进行数值模拟。

2 实验设置

实验是在大连理工大学海岸及近海工程国家重点实验室的多功能水池中进行的，水池长55 m，宽34 m，深0.7 m，一端是由70块造波板组成的推板式多向不规则波造波机。实验地形为坡度均匀的沙坝地形海岸，坡度取1∶40和1∶100两种，坡前静水深分别为0.18 m和0.45 m。沙坝模型与造波板成30°角，用以增加海岸线的长度。模型与其三面水池壁都留有宽度为4.4 m的间隔，以形成沿岸流引起的水池内水体循环，地形的两边缘到造波板附近设置了波导墙，可使水流在外部循环，以避免外部水流对内部水体的干扰，同时在波导墙内壁处设置消浪网，以减轻实验中波浪的反射作用，如图1所示。实验设置坐标系原点取在地形静水岸线上游端点，x正向为垂直岸线离岸方向，y轴沿静水岸线指向下游方向。实验中沙坝断面采用高斯型剖面（图1），沙坝高程为：

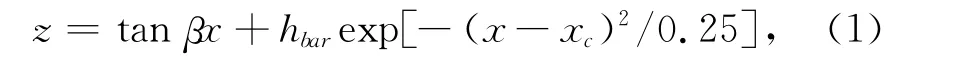
沙坝布置及尺寸参数见表1。

实验中波浪场由垂直于岸线方向排列的3列共60个电容式浪高仪测量，具体布置如图1所示。3列浪高仪分别布置在距沿岸上游边界7 m、12 m和17 m位置，每列都从静水线开始布置，第一列14个浪高仪，间隔1 m；第二列32个浪高仪，前10 m范围间隔0.5 m，10～22 m范围间隔1.0 m；第三列14个浪高仪，前10 m范围间隔1.0 m，10～16 m范围间隔2.0 m。

图1 实验布置（a）及实验照片（b）Fig.1 Experimental layout（a）and actual photo（b）

表1 沙坝布置及其尺寸参数Tab.1 Parameter setting of barred beaches

沿岸流速度场是由28个声学多普勒流速仪（ADV）测量。其中12个ADV用于测量沿岸方向沿岸流的均匀性，该列流速仪对1∶40坡度模型距离岸线3 m，对1∶100坡度模型距离岸线4 m，ADV之间的间隔为2 m，可以覆盖到沿岸方向上下游的范围，如图1所示。另外16个ADV用于测量垂直岸线沿岸流速度剖面，该列流速仪距上游边界14.5 m，对1∶40坡度流速仪间距在距岸线0.25～2 m范围取为0.25 m，在2～6 m范围取为0.5 m，在6～9 m范围取为1.0 m；对1∶100坡度流速仪间距在距岸线1～8 m范围取为0.5 m，在8～10 m范围取为1.0 m，在10～12 m范围取为2.0 m。流速仪测量点与水底间隙为水深的1／3以便测量沿岸流沿水深平均值。实验中数据采集时间为450 s（1∶100坡规则波）、600 s （1∶40坡规则波）和700 s（1∶40和1∶100坡不规则波）。本文平均沿岸流流速均值的取法是截取沿岸流流速充分稳定做平均，从开始采集250 s后到采集结束。本实验采用的ADV对1∶40坡最小水深可以测量到距岸线0.25 m（第一个流速仪位置），对1∶100坡最小水深可以测量到距岸线0.5 m。因此可以测量速度剖面第二峰值。入射波浪包括规则波和不规则波两种，二者都是单向波。表2给出实验中的12组实验波况。表中不规则波高为有效波高。

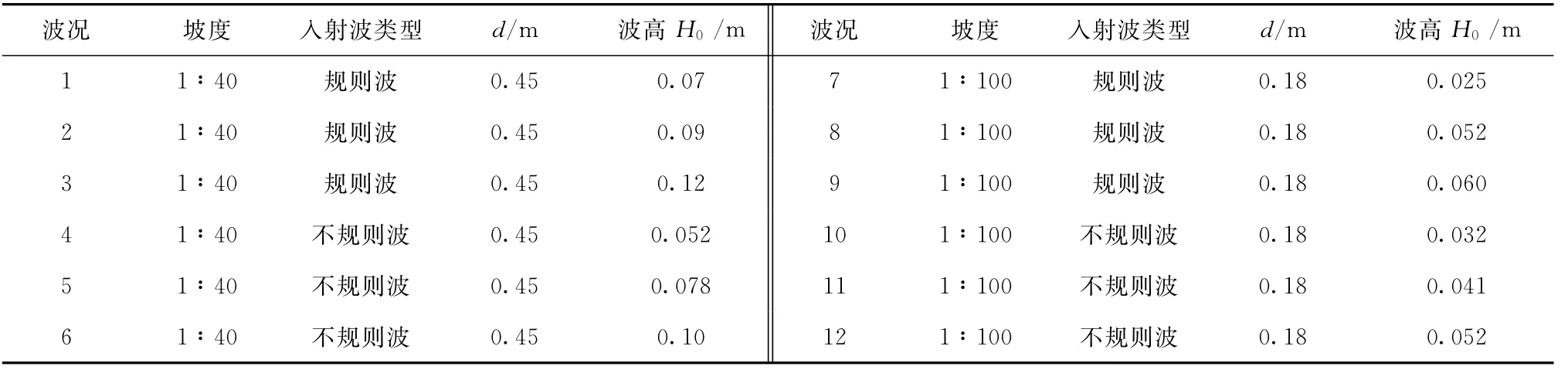
表2 实验波况Tab.2 Wave conditions in experimental study

3 沿岸流沿岸均匀性

Visser［5］采用了水泵循环系统创建双循环水流，通过控制沿岸上游水泵的泵水量和下游的流出宽度来维持沿岸流的均匀性。本实验没有采用这样的靠水泵来维持的水流循环系统，而是在海滩模型周围设置循环渠道，维持由沿岸流引起的水流循环，来提高沿岸流在有限宽度水池内的均匀性，这种循环系统使得实验较为简单，在均匀段更接近于实际海岸，水流循环更自然，如可以允许沿岸流的随着空间和时间而波动，而采用泵循环系统由于泵流量一定，不能允许存在这样的沿岸流波动，这是与实际情况沿岸流情况不符合的。

为了检验沿岸流沿岸的均匀性，实验中通过沿岸布置一列ADV来检测平均沿岸流在沿岸方向的均匀性（布置如上所述）。图3和图4分别给出了沿岸流均匀性较好（T＝1.0 s）和均匀性较差（T＝1.5 s和2.0 s）情况下的沿岸流速度V在沿岸方向的变化。由图3可见，对于不同波浪类型、波高和坡度，在周期为T＝1.0 s小周期情况，沿岸流可以在海岸中间区域（y＝8.5～16.5 m）可以保持较好的均匀性（对规则波1∶40坡这一范围略小，为y＝10.5～16.5 m），靠近上游段（y＝2.5～8.5 m）速度偏小，靠近下游段（y ＝16.5～22.5 m）速度增大，所以在海岸中间段可用作沿岸流测量，而在海岸两端区域沿岸流速度是不符合均匀性要求的。由图4可见，对于坡度1∶40和周期为T＝1.5 s波况，在中间区域存在沿岸流沿岸均匀性（对规则波区域为y＝8.5～16.5 m，对不规则波区域为y＝6.5～12.5 m）。但对大周期T＝2.0 s坡度1∶40的所有波况沿岸均匀性都不好。沿岸流沿着海岸有减小或逐渐增大的趋势，不存在一个较大的取平稳值的区域。对于坡度1∶100较大周期（T＝1.5 s、2.0 s）的波况沿岸流均匀性也都不好。不规则波情况沿岸流沿着海岸有减小或逐渐增大的趋势，不存在一个较大的取平稳值的区域，对规则波情况，这种不均匀性变得更为严重，沿岸流沿岸方向上存在较大波动。综合以上结果可知，对于本实验采用的无水泵帮助的自然循环系统，对小周期T＝1.0 s可以给出沿岸较大范围的均匀沿岸流分布，可以用于本实验研究的沿岸流速度剖面测量。而对于较大周期T＝1.5、2.0 s仅是在1∶40和T＝1.5 s可以有类似于T＝1.0 s的沿岸流均匀性，其他情况由于波浪折射较大，使得海岸两侧边界对内部区域波浪传播存在一定影响，所以沿岸流沿岸均匀性较差。

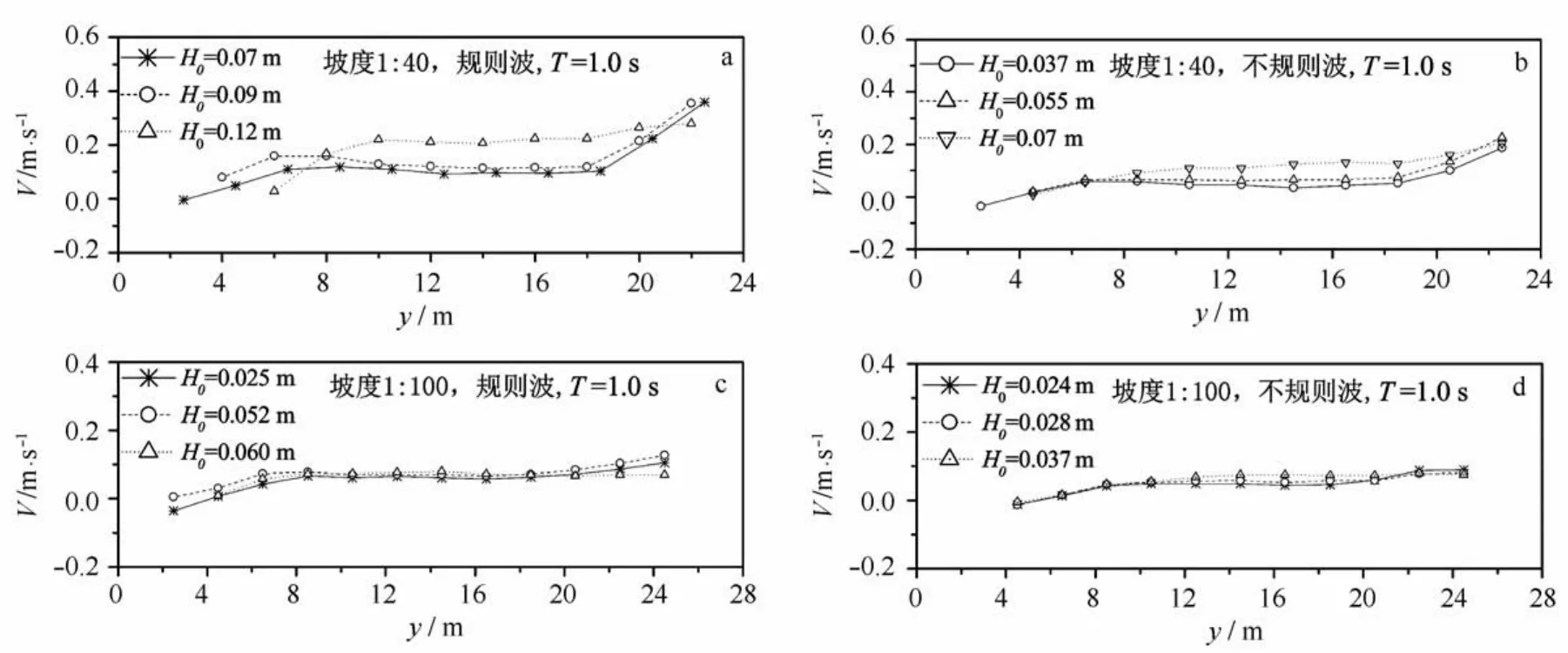
图3 小周期波况沿岸流沿岸方向速度剖面（T＝1.0 s）Fig.3 Alongshore distribution of mean longshore currents under short periodic wave conditions（T＝1.0 s）

图4 大周期波况沿岸流沿岸方向速度剖面（T＝1.5 s和2.0 s）Fig.4 Alongshore distribution of mean longshore currents under long periodic wave conditions（T＝1.5 s and 2.0 s）

4 沿岸流速度剖面特征

为了讨论沿岸流速度剖面特性，选取沿岸流速度在沿岸方向均匀性较好（见上节讨论）的小周期1.0 s波况进行分析。图5和图6分别给出了两个坡度的波高、波浪增减水和沿岸流的垂直岸线剖面图，图中虚线表示水底沙坝地形。表3给出了各波况的破碎点位置、两速度峰值的位置和数值以及比值。

图5 1∶40坡波高、增减水和沿岸流速的垂直岸线剖面Fig.5 Cross-shore profiles of wave height，set-up of the mean water level and longshore current velocity for slopes with gradient of 1∶40

由图5和图6可以看出，沙坝地形下波浪将发生两次波浪破碎。第一次破碎发生在沙坝或沙坝外侧，第二次破碎发生在靠近岸线位置，位置分别由表3中由xxbar和x／xbar给出。图5c～d和6c～d可以看出：随着入射波高的增大，增减水数值也增大。由图5e～5f和6e～6f可以看出，平均沿岸流速度剖面出现两个速度峰值的双峰值剖面特征：第一峰值出现在沙坝向岸侧（1∶40坡度：／xbar＝0.90，1∶100坡度：／xbar＝0.93），第二个峰值出现在靠近岸线处位置（1∶40坡度：xbar＝0.25，1∶100坡度：／x＝0.21）。在沙坝外侧波浪破碎前沿岸流流bar速度值很小（这是因为在破波带外的沿岸流速只由侧向混合产生的紊动切应力驱动，并未产生大的沿岸流）。当波浪在沙坝上破碎使得沿岸流流速迅速增大，在／xbar＝0.90（1∶40坡度）和0.93（1∶100坡度）出现沿岸流速度第一峰值。这不同于Reniers等的实验室模型试验（沿岸流速度最大值发生在沙坝顶附近，即x／xbar＝1.0），这是因为对于沿岸均匀沙坝地形沿岸压力梯度太弱而不能够使速度峰值移动到沟槽位置，并且在沙坝顶和沟槽之间没有设置流速测量点；也不同于DELILAH和PNEC等现场观测实验结果（由于现场沙坝沿岸不均匀而产生明显的压力梯度使得沿岸流速度剖面的最大值出现在沙坝沟槽里）。当波浪到达岸线附近，在／xbar＝0.25（1∶40坡度）和0.21（1∶100坡度）出现了沿岸流速度第二峰值。由于第二峰值的产生是受二次破碎位置决定的，在同一地形下，沙坝使得不同波况的波浪破碎后波高相差不多，从而使得二次破碎发生的位置接近，使得第二峰值大致发生在相同位置。从表3可以看出，沿岸流二峰值的速度比值基本不变，比值大致保持为0.41（1∶40坡度）和0.27（1∶100坡度）。

图6 1∶100坡波高、增减水和沿岸流速的垂直岸线剖面Fig.6 Cross-shore profiles of wave height，set-up of the mean water level and longshore current velocity for slopes with gradient of 1∶100

表3 沿岸流双峰速度剖面特征值Tab.3 Characteristic values of bimodal velocity profiles of longshore currents

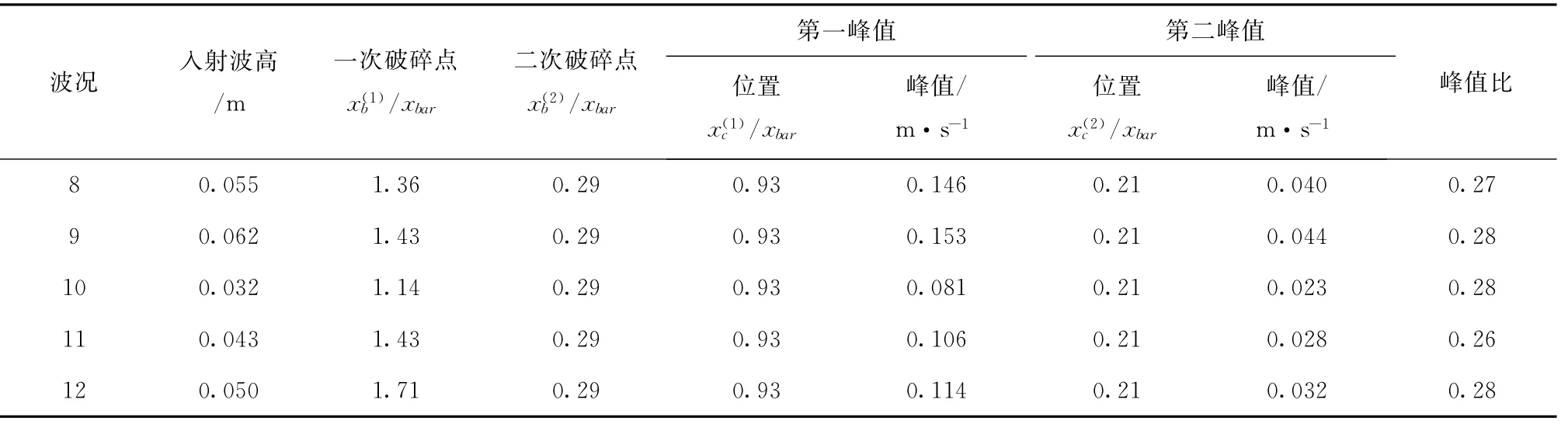
续表3

波浪通过水滚能量耗散所需的时间使得沿岸流两速度峰值和二次破碎的位置存在空间滞后的现象。因不规则波破碎带较宽，不好确定破碎位置，只给出规则波情况。第一峰值和第一次破碎位置：1∶40坡度最小滞后1.5 m（H0＝0.07 m）和最大滞后2.5 m （H0＝0.112 m），1∶100坡度最小滞后1.5 m（规则波H0＝0.025 m）和最大滞后3.5 m（规则波H0＝0.062 m）。第二峰值和第二次破碎位置：1∶40坡度最小滞后0.25 m（H0＝0.07 m）和最大滞后0.75 m（H0＝0.112 m），1∶100坡度滞后0.5 m。

随着入射波高增大，沿岸流速度剖面变宽，主要表现在沙坝离岸侧速度剖面明显有离岸变化的趋势，这是因为随着波高增大，波浪破碎点位置离岸变化所造成的。波高增大也使得沿岸流速度值增大，但并没有改变沿岸流二峰值的比值。不规则波作用下的沿岸流速度剖面较规则波平缓光滑，这是因为不规则波浪破碎状态与规则波破碎状况间的差别决定了相应沿岸流分布的不同，表现在不规则波波浪破碎区域宽于规则波波况。1∶100坡度的速度剖面宽于1∶40坡度，这是因为1∶100坡度水深较浅，波浪破碎早，形成更宽的破波带。沿岸流速度两峰值的比值随坡度的增大而变大。

5 数值模拟

本节建立了基于波能守恒方程的沿岸流数值模型，对波高、波浪增减水和沿岸流速度进行数值模拟。模型中引入水滚的概念来考虑波浪破碎，为了平衡水滚的重力而在波前产生剪应力，此剪应力所做的功等于水滚能量的损耗。

波能量守恒方程：

式中，Ew为波能量，cg是波群速度，θ是波浪相对于海岸垂线方向的入射角，由Snell定律求得，即

式中，θ0、c0分别是入射波在破碎带外某点处的入射角和波速，波速c由下式求得：

式中，ω是角频率，k是波数，由线性波浪色散关系给出：

S为波浪破碎能量耗散，针对两种波浪类型，都采用Roelvink能量损耗公式：

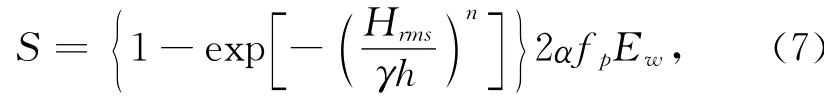
式中，Hrms为均方根波高；γ为波浪破碎指标，规则波采用0.7，不规则波采用0.55；α也表示波浪破碎强度，为一阶参数；fp是波峰频率；n为指数。

水滚能量方程：

式中，Er为水滚能量，可由Svendsen和Putrevu［6］的水滚能量公式计算：

式中，L为波长，A为水滚的面积。

式（8）右端的¯τt是波浪和水滚交界面之间的剪应力，稳定水滚的剪应力可以用公式求得：

式中，β为水滚前倾角，Walstra等［17］指出水滚前倾角是个小于0.1的数，经验公式如下：

由此可知：坡度越小，kh越小，β就越小。基于Reniers实验1∶20坡度采用0.1，故本文对1∶40坡度取0.08，对1∶100坡度取0.03。

平均水平面的增减水方程［6］：

式中，¯η是平均水平面的增减水。式中等号左边第一项表示和波浪运动相关的辐射应力梯度；第二项表示水滚的影响；第三项表示由于平均水平面的增减水而产生的压力梯度。Sxx，w为波浪辐射应力：

Sxx，r为水滚辐射应力：

在求得了因为波浪破碎而产生的辐射应力沿垂直海岸方向的分布之后，可以用沿岸线方向的动量方程来求解沿岸流速度：

方程左端第一项表示由于波浪破碎而产生的力，第二项表示由于流体紊动而产生的侧向混合，右端项表示沿岸方向的波浪平均底剪应力。传统的波浪力由线性波浪理论给出：

而考虑包括水滚在内的辐射应力由Deigaard给出

方程（17）中的紊动侧混项可以用Longuet-Higgins的扩散渗透项模拟：

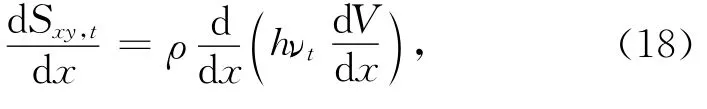
式中，V为沿水深平均的沿岸流速度，νt为紊流粘滞系数，本文采用了Longuet-Higgins方法：

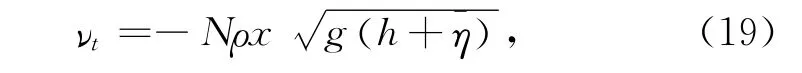
式中，N为无量纲参数，两坡度均取为0.003。底摩擦阻力为：

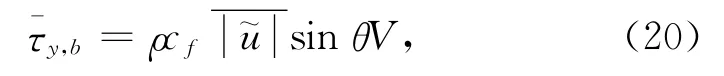
式中，cf为摩擦系数，对1∶40坡取为0.02，对1∶100坡取为0.015。˜u是沿波浪传播方向的瞬时波浪水质点速度，可由下式求得：

图7给出了几个代表波况的波高、增减水和平均沿岸流的数值模拟结果和实验结果的比较。对规则波，图中给出了不考虑水滚影响的速度剖面（图中虚线表示），对不规则波，图中给出了不考虑侧混影响的速度剖面（图中虚线表示）。图中可以看出，对于1∶100坡度，数值模拟的两个峰值位置和实验结果相吻合，小波高情况第二峰值数值高于实验结果。对于1∶40坡，不规则波情况，数值模拟和实验结果吻合较好，而规则波波况的沿岸流二峰值的数值模拟数值较实验数值偏低，位置偏向岸线。水滚和侧混对沿岸流速度剖面的影响情况：水滚将使得沿岸流速度剖面向岸线的方向有一定的偏移，使得两个峰值的位置向岸线偏移和速度值增大；而侧混影响则是使得沿岸流速度剖面第一峰值变宽而扁，而对第二峰值影响很小。

6 结论

本文通过对1∶40和1∶100两种坡度沙坝海岸上的沿岸流进行测量，来研究沙坝地形的沿岸流速度双峰值剖面特征，特别是第二个峰值的特征。第一峰值发生在沙坝向岸侧面的中部，第二个峰值发生在靠近岸线处。同一坡度情况两个峰值的位置和比值，不受入射波类型、入射波高的影响，而是取决于沙坝的位置。随着入射波高增大，沿岸流速度值也随之增大，沿岸流速度剖面变宽，主要表现在沙坝离岸侧的速度剖面明显有离岸变化的趋势，但速度二峰值的比值（第二峰值／第一峰值）不受波高的影响。相比规则波浪作用下流速集中的状态，不规则波作用下的沿岸流速度剖面较宽，而且平缓光滑。1∶100缓坡地形条件下，波生沿岸流影响范围普遍大于1∶40陡坡地形情况。两峰值的比值随坡度的增大而变大，两峰值比值的变化体现在二峰值的变化。

通过对数值模拟和实验结果的比较，对1∶100坡度两者吻合较好，对1∶40坡度规则波二峰值位置及峰值有些偏移。水滚将使得沿岸流速度剖面向岸线的方向有一定的偏移，使得两个峰值的位置向岸线偏移和速度值增大；而侧混影响使得沿岸流速度剖面第一峰值变宽而扁，而对第二峰值影响很小。

图7 数值模拟（线型）和实验结果（×○△）比较Fig.7 Comparison between numerical results（solid and dash lines）and measured data（×○△）

［1］Ruessink B G，Miles J R，Feddersen F，et al.Modeling the alongshore current on barred beaches［J］.Journal of Geophysical Research：Oceans（1978－2012），2001，106（C10）：22451－22463.

［2］Feddersen F，Guza R，Elgar S，et al.Alongshore momentum balances in the nearshore［J］.Journal of Geophysical Research，1998，103（C8）：15667－15676.

［3］Thornton E B，Guza R T.Surf zone longshore current and random waves：field data and models［J］.Journal of Physical Oceanography，1986，16：1165－1178.

［4］Church J C，Thornton E B.Effects of breaking wave induced turbulence within a longshore current model［J］.Coastal Engineering，1993，20（1）：1－28.

［5］Visser P J.Laboratory measurements of uniform longshore currents［J］.Coastal Engineering，1991，15（5／6）：563－593.

［6］Svendsen I A，Putrevu U.Nearshore mixing and dispersion［J］.Proceedings of the Royal Society of London.Series A：Mathematical and Physical Sciences，1994，445（1925）：561－576.

［7］Birkemeier W A.Delilah nearshore processes experiment：Data summary，miscellaneous reports.Coastal Eng.Res.Cent.，Field Res.Facil.，U.S.Army Eng.Waterw.Exp.Sta.，Vicksburg，Miss，1991.

［8］Kuriyama Y，Nakatsukasa T.A one-dimensional model for undertow and longshore current on a barred beach［J］.Coastal Engineering，2000，40：39－58.

［9］Reniers A J H M，Battjes J A.A laboratory study of longshore currents over barred and non-barred beaches［J］.Coastal Engineering，1997，30：1－22.

［10］Hamilton D G，Ebersole B A.Establishing uniform longshore currents in a large-scale sediment transport facility［J］.Coastal Engineering，2001，42（3）：199－218.

［11］邹志利，常梅，邱大洪，等.沿岸流的实验研究［J］.水动力学研究与进展，2002，17（2）：174－180.

［12］Zou Z L，Wang S P，Qiu D H，et al.Longshore currents of regular waves on different beaches［J］.Acta Oceanologica Sinica，2003，22（1）：123 －132.

［13］孙涛，韩光，陶建华.波生沿岸流数值模拟研究及其实验验证［J］.水利学报，2002（11）：1－7.

［14］Zheng J，Tang Y.Numerical simulation of spatial lag between wave breaking point and location of maximum location of maximum wave-induced current［J］.China Ocean Engineering，2009，23（01）：59－71.

［15］解鸣晓，张玮.近岸波生流运动三维数值模拟及验证［J］.水科学进展，2011，22（3）：391－399.

［16］房克照，刘忠波，邹志利，等.波生沿岸流数值模拟［J］.水科学进展，2013，24（2）：258－265.

［17］Walstra D J R，Mocke G P，Smit F.Roller contributions as inferred from inverse modelling techniques［J］.Coastal Engineering Proceedings，1996，1（25）：1205－1218.

Cross-shore distribution feature of longshore currents over barred beaches

Wang Yan1，Zou Zhili1
（1.The State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China）

The experimental study on wave-driven longshore currents on barred beaches and numerical simulations which were based on wave energy conservation equation，were conducted to investigate the cross-shore distribution feature of velocity profiles of mean longshore currents，with emphasis on the second peak of longshore currents.The distribution feature of longshore currents has the velocity profile with bimodal characteristics.The larger one occurs on the middle part of lateral side of barred beaches and the smaller one is close to the shoreline，which corresponds to the first and second wave breaking respectively.The above features have been discussed by considering the effects of wave height，wave type and beach slope.The locations of two peaks and their ratio（i.e.，higher one／smaller one）do not depend on wave type and wave height，but the location of barred beaches.Numerical simulations were also performed to compute the measured velocity profile with the emphasis on the effect of several factors such as lateral mixing，bottom friction and surface rollers on numerical results.

bimodal profiles；two peak values；wave breaking；barred beaches

TV139.2

A

0253-4193（2014）11-0120-11

2013-09-28；

2014-01-23。

国家自然科学基金（51079024，10672034）。

王彦（1982－），男，吉林省梨树县人，博士研究生，主要从事海岸水动力研究。E-mail：ywang0412＠163.com

王彦，邹志利.沙坝海岸沿岸流速度剖面特征研究［J］.海洋学报，2014，36（11）：120－130，

10.3969／j.issn.0253-4193.2014.11.014

Wang Yan，Zou Zhili.Cross-shore distribution feature of longshore currents over barred beaches［J］.Acta Oceanologica Sinica（in Chinese），2014，36（11）：120－130，doi：10.3969／j.issn.0253-4193.2014.11.014