模块化多电平变换器三种调制策略及电压平衡控制仿真与对比研究

武晓堃，王奎，万磊，2，郑泽东，李永东，3

(1．清华大学电机工程及应用电子技术系电力系统及发电设备控制和仿真国家重点实验室，北京100084; 2．中国电力科学研究院，北京100192;3．新疆大学电气学院，新疆乌鲁木齐830046)

模块化多电平变换器三种调制策略及电压平衡控制仿真与对比研究

武晓堃1，王奎1，万磊1，2，郑泽东1，李永东1，3

(1．清华大学电机工程及应用电子技术系电力系统及发电设备控制和仿真国家重点实验室，北京100084; 2．中国电力科学研究院，北京100192;3．新疆大学电气学院，新疆乌鲁木齐830046)

模块化多电平变换器作为一种新型的多电平拓扑，因为适用于电压源换流型直流输电场合而得到了广泛研究。本文介绍了模块化多电平变换器的拓扑结构和工作原理，并对常用于模块化多电平变换器拓扑的载波移相、最近电平逼近和载波层叠调制策略以及相应的电容电压平衡算法进行了分析，并在PSCAD/EMTDC下搭建了31电平的模块化多电平变换器仿真模型，分别实现了三种调制策略及其电容电压平衡算法，比较了不同调制策略在电压谐波、电容电压平衡、开关频率等方面的表现，并给出了不同调制策略的特点。

模块化多电平变换器;载波层叠调制;最近电平逼近调制;载波移相调制;电容电压平衡

1 引言

在离岸风电场、跨湾输电等输电场合，直流输电因为可以克服电容效应而被人们愈发重视［1，2］。传统的VSC-HVDC直流输电系统主要以两电平和三电平为主，因此受器件耐压限制，所能达到的电压等级不高，谐波较大。其中ABB公司的IGBT串联两电平拓扑，虽然提高了电压等级，但是存在着串联模块均压以及同时触发等问题。2002年，由德国学者提出了一种新型的多电平拓扑［3，4］，即模块化多电平变换器(Modular Multilevel Converter，MMC)，该结构具有高度模块化，通过模块级联就可以实现电压等级的提升［5-7］。西门子公司将该拓扑转化为了专利和产品应用于直流输电等场合，其中美国的Transbay工程，每相子模块级联数为200，输送功率可以达到400MW［5］。MMC一提出就受到了广泛关注，学者们对于MMC建模以及内部环流机制进行了大量研究［8-10］。此外，由于悬浮电容电压的平衡控制策略受制于采用的底层控制策略，因此对于MMC的底层控制以及子模块均压问题是一个研究热点［11-16］。

本文针对MMC中主要采用的载波层叠、载波移相和最近电平逼近三种调制策略以及相应的子模块电容电压平衡策略进行了分析，并在PSCAD/ EMTDC下搭建了一个31电平的仿真模型对三种调制策略进行仿真研究。对分别采用三种调制策略的模块化多电平变换器在电压谐波、子模块电容电压平衡、开关频率等方面进行了仿真对比，总结了三种调制策略各自的优点和缺点。

2 模块化多电平变换器的基本结构

图1为模块化多电平变换器和子模块的拓扑结构，每相桥臂由上下两个桥臂组成，其中每个桥臂含有N个结构相同的子模块(Sub-module，SM)，每个桥臂还包括一个小电感，该电感的主要作用是限制桥臂内不同的子模块接入时和母线之间的电压跳变而引起的尖峰电流以及母线与桥臂之间的环流。每个子模块由两个IGBT和电容组成一个半桥结构，UC为子模块的电容电压，uSM为子模块的输出电压。当上管S1导通、下管S2关断时，定义这种状态为“投入”状态，此时子模块的输出电压为电容电压;当上管S1关断、下管S2开通时，定义这种状态为“切除”状态，此时子模块的输出电压为0。即存在下式:

图1 MMC基本结构Fig．1Basic structure of MMC

从MMC的结构上可以看出，其拓扑结构具有如下优点:

(1)结构高度模块化，每个桥臂都由基本单元级联而成。

(2)易于通过串联实现高电压输出，相比传统的电容或者二极管箝位，节省箝位二极管或者箝位电容。

(3)具有公共直流母线，可以实现四象限运行。

3 模块化多电平变换器的调制策略

MMC拓扑作为多电平拓扑的一种，理论上可以采用适用于多电平的各种调制策略，如空间矢量调制、特定谐波消去调制等方法［15］。但是考虑到应用于直流输电系统场合中，MMC换流器的电平数经常达到几十甚至上百，所以MMC的调制策略和普通的多电平调制又有所区别。在文献中人们主要集中研究的调制策略可以概括分为载波层叠PWM(Carrier Stacked PWM)、最近电平逼近调制［15，16］(Nearest Level Modulation)和载波移相PWM［11-14］(Carrier Phase Shifted PWM)。

3.1 载波层叠PWM及电容电压平衡策略

在载波层叠调制策略中，每个子模块有三种工作状态:Y=0(切除状态)，Y=1(投入状态)，Y=d (PWM状态)。每个桥臂只有一个子模块工作在PWM模式，其余子模块都工作在投入或者切除状态，Y=0对应于在一周期内载波均高于参考波，此时子模块的下管应该保持导通;Y=1对应于在一周期内载波均低于参考波，此时子模块的上管应该保持导通;Y=d对应于在一周期内载波会和参考波交叉，此时子模块应以一定的占空比导通。调制策略如图2(a)所示，其中三角波为载波，正弦波为参考波，L为各个载波的层级。

图2 载波层叠PWM及其电容电压平衡控制Fig．2Modulation and capacitor voltage balance strategy of carrier stacked PWM

模块化多电平变换器的控制必须要考虑子模块电容电压的平衡，否则拓扑将不能正常工作。子模块可以工作在投入、切除以及PWM状态，所以根据桥臂电流方向不同以及工作状态的不同，子模块可能处于充电、放电以及旁路。电容电压平衡的控制策略如图2(b)所示。首先根据参考电压uref得到此时处于Y=0的子模块数量NY0和处于Y=1的子模块数量NY1;之后对桥臂的子模块的电容电压排序;当桥臂电流iarm＞0(充电方向)，将该桥臂电容电压最低的NY1个子模块投入充电，次低的1个子模块处于PWM状态，其余子模块切除。反之则将该桥臂电容电压最高的NY1个子模块投入放电。

3.2 最近电平逼近调制及电容电压平衡策略

最近电平逼近方法是一种适用于电平数较多的拓扑结构的调制方法，其调制方式如图3(a)所示，将控制器得到的桥臂参考电压uref除以子模块电容电压UC取整得到最终投入的子模块个数NON，关于取整方法，有最近取整、去尾取整等，一般常用最近取整，比如当uref/UC=2.4时，NON等于2即投入2个子模块，当uref/UC=2.6时，NON等于3即投入3个子模块。换流器根据各桥臂投入的子模块个数NON以及电容电压平衡算法，最终实现子模块的投入和切除。

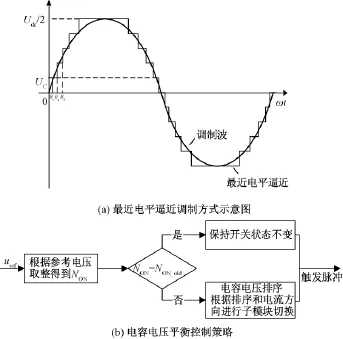
图3 最近电平逼近调制及其电容电压平衡控制Fig．3Modulation and capacitor voltage balance strategy of nearest level modulation

为了实现各个子模块的电容电压的平衡，需要根据各个电容电压大小以及桥臂电流方向合理选择投入和切除的子模块。传统的电容电压平衡策略在每个开关周期对子模块的电容电压进行排序，当电流为充电方向时，将该相桥臂电压最低的NON个子模块投入，反之亦然。这种方法的好处是可以迅速缩小各个子模块之间的电压偏差，但是各个子模块之间切换过于频繁导致开关管开关损耗较大。为了在保证子模块电容电压平衡的情况下减小开关管的动作次数，可以采用一种改进的电容电压平衡策略，如图3(b)所示。定义上一个时刻投入的子模块数为NON_old，在输出电压的电平变化时，即NON≠NON_old时才进行电容电压排序，并依照此时的电容电压排序情况以及电流方向进行子模块的切换，在输出电压电平无变化，即NON=NON_old时，保持此时的开关信号。这种改进的平衡控制策略能减少子模块的切换，降低开关管的损耗。

3.3 载波移相PWM及电容电压平衡策略

类似于H桥型级联结构，模块化多电平变换器同样可以采用载波移相的控制策略。对于N+1电平的模块化多电平变换器结构，每个桥臂含有N个级联的子模块，需要采用N组三角载波，且载波的频率相同但是相位错开2π/N角度。设桥臂的参考电压为，各个子模块的参考电压为，i=1，2，…，N，则桥臂所有子模块的参考电压之和等于桥臂参考电压的N倍。

N个子模块参考电压和N组载波相比较产生N组PWM脉冲。图4(a)为载波移相PWM的原理示意，图中为五电平。

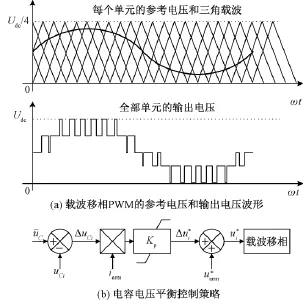
图4 载波移相PWM及其电容电压平衡控制Fig．4Modulation and capacitor voltage balance strategy of carrier phase shifted PWM

在理想情况下，如果各个桥臂子模块的参考电压相等且为桥臂参考电压，即=，此时电容电压是可以实现自平衡的;但在非理想或者动态条件下，由于输出功率的波动、计算量化误差及PWM死区等问题，电容电压将可能发散，因此仍然需要电容电压的平衡控制策略。在满足式(2)即保证桥臂输出特性不变的约束条件下，通过小范围调整桥臂内部各个子模块的参考电压，可以实现电容电压的平衡［14］。文献［14］给出了一种通过加入附加的平衡控制分量实现电容电压平衡的方法，如图4(b)所示。uCi为第i个子模块的电容电压，为该桥臂N个子模块的电容电压平均值;子模块i的电容电压和平均值之间的误差为ΔuCi，作为附加平衡控制的输入，ΔuCi和桥臂电流iarm的乘积经过比例环之后生成附加参考电压，叠加在桥臂参考电压上，作为生成的最终参考电压。

式中，Kp为比例系数，通过调节其正负来实现桥臂电流方向和子模块的充放电状态的匹配。

4 调制策略的仿真与分析

为了比较上述几种控制方法的特点和电容电压平衡控制的效果，在PSCAD/EMTDC平台上搭建了一个仿真模型。仿真系统为三相31电平，即每个桥臂有30个子模块，子模块电容值为2mF，桥臂的电抗为5mH，逆变器直流侧电压Udc=30kV，桥臂负载侧为三相理想对称的阻感负载，负载电阻100Ω，负载电感10mH。仿真中的控制流程图如图5所示，首先计算逆变器的输出参考电压，之后根据采集得到的各个子模块电容电压以及负载电流，利用上述调制策略以及电容电压平衡策略决定各个单元的开关管信号，并更新PWM。

图5 仿真控制流程图Fig．5Control flowchart in simulation

仿真中，载波层叠的载波频率和最近电平逼近的仿真模型的控制频率为5000Hz，载波移相中，单个子模块的载波频率为166.67Hz，因此30个子模块的等效输出电压频率同样为5000Hz。图6为三种调制策略下第一个子模块SM1的上侧IGBT的触发脉冲，比较图6(a)、图6(b)和图6(c)可以看出，载波层叠调制下开关次数最多，载波移相调制下的开关次数最少，符合控制策略的特点。

进一步的，在额定工况下，本文对A相上桥臂所有30个子模块的上侧IGBT开关次数进行了统计，折算后的单个器件平均开关频率fsw_dev可以表示为［17］:

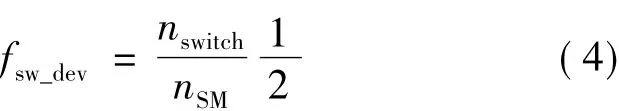
式中，nswitch为单位时间内统计得到的一个桥臂上所有子模块的上侧IGBT开关次数总和(开通和关断各算一次);nSM为一个桥臂的子模块总数。由此得到不同调制策略下，MMC器件的平均开关频率，结果见表1。

图6 SM1上侧IGBT触发脉冲Fig．6Trigger signal of upper IGBT in SM1

表1 不同调制策略下的器件平均开关频率Tab．1Average switch frequency of different modulation strategies

从表1可以看出，采用载波层叠的开关频率最高(1021Hz)，最近电平逼近因为采用了降低开关频率的控制方法所以开关频率相比载波层叠有所降低(630Hz)，而载波移相控制策略的子模块开关频率取决于三角载波的频率，各个子模块的开关频率相同且是固定的(167Hz)。通常情况下，开关频率和换流器的开关损耗呈正比，所以采用载波层叠控制的开关损耗最大，载波移相的开关损耗最小。

图7为采用三种调制策略下的输出相电压波形和谐波分析图，输出相电压均为31电平，图中谐波幅值为相对基波幅值的百分比。通过谐波分析可知，载波层叠的谐波主要集中在5000Hz左右，即控制器的触发频率。最近电平逼近调制的谐波除了控制器的触发频率以外还含有大量低次谐波，载波移相调制的谐波主要为高次谐波。从三种调制方法的总体谐波畸变率来说，载波移相的谐波最小(THD= 3.13%)，最近电平逼近其次(THD=4.00%)，而载波层叠的谐波最差(THD=4.61%)。

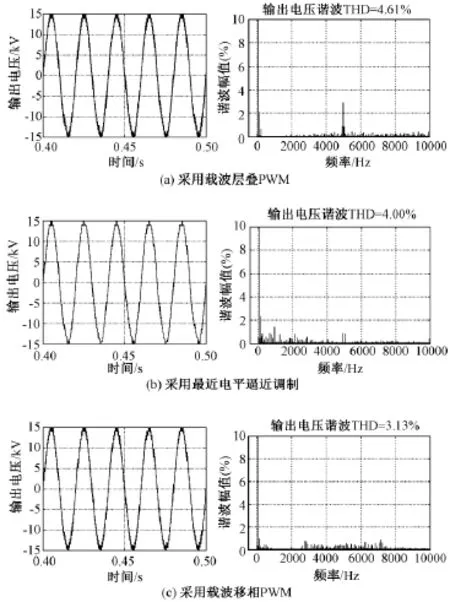
图7 A相输出电压Fig．7Output voltage of phase A

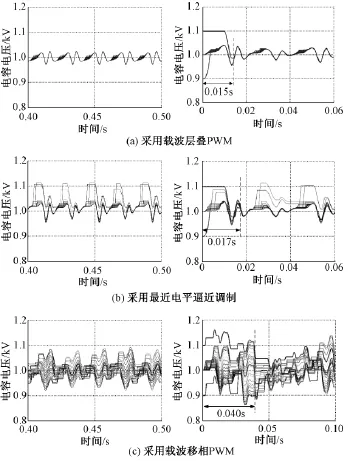
图8 A相上桥臂子模块电容电压波动Fig．8Capacitor voltage fluctuation of upper arm in phase A

图8为三种调制策略下的A相上桥臂电容电压的波动情况，其中左侧的仿真结果为不同调制策略时的稳态波动情况，右侧的是当电容电压初始值不同时的电容电压调节情况。为了研究不同控制策略对电容电压的调节速度，在初始时设置第一个子模块的电容电压初值为UC1=0.9kV，设置第二个子模块的电容电压初值为UC2=1.1kV。三种调制方法均实现了电容电压的平衡，但是在电容电压的波动范围和响应速度上存在一定偏差。载波层叠调制中采用的电容电压平衡策略在每个开关周期都会进行电容电压排序以及子模块的切换，所以电容电压波动最小，波动范围为±0.05kV;在最近电平逼近调制中，虽然控制器的触发频率和载波层叠一致，但是因为采用了减少开关动作的电容电压平衡策略，所以电容电压波动大于载波层叠，波动范围大概± 0.1kV;载波移相中子模块的电压波动范围大概为±0.08kV。在电容电压调节速度上，载波层叠PWM大概经过0.015s，各个电容的波动就基本一致，而这个时间对于最近电平逼近调制以及载波移相PWM分别是0.017s和0.04s。产生这一现象的原因是因为载波层叠PWM中的子模块切换更为频繁，所以电容电压波动最小，且电容电压调节速度最快;而载波移相PWM中，电容电压的调节受比例系数Kp影响，当Kp较大时调节速度较快，但是相应的电容电压的波动也会增加，当Kp较小时，调节速度较慢，在极端情况下，当Kp为0时，电容电压的稳态误差将无法消除。

5 结论

在MMC-HVDC场合，因为子模块数极多，此时载波层叠PWM因为复杂的电容电压排序算法以及较高的开关频率已经不再适用。而载波移相和最近电平逼近各有优缺点，载波移相的主要优点是开关频率固定，但是当电容电压偏差较大时，平衡速度较慢，而针对每个子模块设计平衡控制器的平衡策略数据计算量较大且硬件难以实现。最近电平逼近的主要优点是控制简单，硬件易于实现，且当子模块数极多时，输出谐波以低次谐波为主的劣势将逐渐消失，另外最近电平逼近调制策略中开关频率可以进一步降低甚至被固定。因此可以预见，对于MMCHVDC场合，最近电平逼近调制将成为主要的调制策略。

［1］徐政，陈海荣(Xu Zheng，Chen Hairong)．电压源换流器型直流输电技术综述(Review and application of VSC HVDC)［J］．高电压技术(High Voltage Engineering)，2007，33(1):1-10．

［2］Bresesti P，Kling W L，Hendriks R L，et al．HVDC connection of offshore wind farms to the transmission system［J］．IEEE Transactions on Energy Conversion，2007，22 (1):37-43．

［3］Lesnicar A，Marquardt R．An innovative modular multilevel converter topology suitable for a wide power range［A］．2003 IEEE Bologna Power Tech Conference Proceedings［C］．2003.3-6．

［4］Glinka M，Marquardt R．A new AC/AC-multilevel converter family applied to a single-phase converter［A］．The Fifth International Conference on Power Electronics and Drive Systems［C］．2003.16-23．

［5］韦延方，卫志农，孙国强，等(Wei Yanfang，Wei Zhinong，Sun Guoqiang，et al．)．适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展(New prospects of modular multilevel converter applied to voltage source converter high voltage direct current transmission)［J］．高电压技术(High Voltage Engineering)，2012，38(5):1243-1252．

［6］韦延方，卫志农，孙国强，等(Wei Yanfang，Wei Zhinong，Sun Guoqiang，et al．)．一种新型的高压直流输电技术—MMC-HVDC(New HVDC power transmission technology:MMC-HVDC)［J］．电力自动化设备(Electric Power Automation Equipment)，2012，32 (7):1-9．

［7］Friedrich K．Modern HVDC PLUS application of VSC in modular multilevel converter topology［A］．IEEE International Symposium on Industrial Electronics［C］．Bari，Italy，2010.3807-3810．

［8］Solas E，Abad G，Barrena J A，et al．Modelling，simulation and control of modular multilevel converter［A］．Proceedings of 14th International Power Electronics and Motion Control Conference(EPE-PEMC)［C］．Ohrid，2010．T2-90-T2-96．

［9］潘武略，徐政，张静，等(Pan Wulue，Xu Zheng，Zhang Jing，et al．)．电压源换流器型直流输电换流器损耗分析(Dissipation analysis of VSC-HVDC converter)［J］．中国电机工程学报(Proceedings of the CSEE)，2008，28(21):7-14．

［10］屠卿瑞，徐政，郑翔，等(Tu Qingrui，Xu Zheng，Zheng Xiang，et al．)．模块化多电平换流器型直流输电内部环流机理分析(Mechanism analysis on the circulating current in modular multilevel converter based HVDC)［J］．高电压技术(High Voltage Engineering)，2010，36(2):547-552．

［11］Qingrui Tu，Zheng Xu，Lie Xu．Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters［J］．IEEE Transactions on Power Delivery，2011，26(3):2009-2017．

［12］Hagiwara M，Nishimura K，Akagi H．A medium-voltage motor drive with a modular multilevel PWM inverter［J］．IEEE Transactions on Power Electronics，2010，25(7): 1786-1799．

［13］Hagiwara M，Akagi H．Control and experiment of pulsewidth-modulated modular multilevel converters［J］．IEEE Transactions on Power Electronics，2009，24(7):1737-1746．

［14］李笑倩，宋强，刘文华，等(Li Xiaoqian，Song Qiang，Liu Wenhua，et al．)．采用载波移相调制的模块化多电平换流器电容电压平衡控制(Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32(9): 49-55．

［15］屠卿瑞，徐政，郑翔，等(Tu Qingrui，Xu Zheng，Zheng Xiang，et al．)．一种优化的模块化多电平换流器电压均衡控制方法(An optimized voltage balancing method for modular multilevel converter)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2011，26(5):15-20．

(，cont．on p.29)(，cont．from p.9)

［16］王楚，宋平岗，李云丰(Wang Chu，Song Pinggang，Li Yunfeng)．模块化多电平变流器的最近电平逼近调制策略(The nearest level modultaion strategy for modular multilevel converter)［J］．大功率变流技术(High Power Converter Technology)，2012，(4):20-22．

［17］Wu Bin．High-power converters and AC drives［M］．Hoboken:IEEE Press，John Wiley＆Sons，2006．

Simulation and comparative study of three modulation strategies and voltage balance control in modular multilevel converter

WU Xiao-kun1，WANG Kui1，WAN Lei1，2，ZHENG Ze-dong1，LI Yong-dong1，3
(1．State Key Lab of Control and Simulation of Power Systems and Generation Equipments，Department of Electrical Engineering，Tsinghua University，Beijing 100084，China;2．China Electric Power Research Institute，Beijing 100192，China;3．Department of Electrical Engineering，Xinjiang University，Urumqi 830046，China)

As a novel multilevel topology，the modular multilevel converter(MMC)has been widely studied because of its application in HVDC．In this paper，the commonly used modulation strategies in MMC，carrier stacked PWM，nearest level modulation，and carrier phase shifted PWM are introduced．To balance the capacitor voltage of sub-module，several different capacitor voltage balancing algorithms are also analyzed．The carrier stacked PWM has the highest switch frequency which leads to the best capacitor voltage balancing performance．The nearest level modulation is easy to implement and the switching frequency can be restricted to a low rate．The carrier phase shifted PWM has a fixed switching frequency．To compare the three modulation strategies，a 31-level simulation model of MMC is built in PSCAD/EMTDC．The three modulation strategies and capacitor voltage balancing algorithm are realized in the simulation model．The performance of the capacitor voltage fluctuation，switching frequency，voltage harmonics and other aspect of performance are compared．

modular multilevel converter;carrier stacked PWM;nearest level modulation;carrier phase shifted PWM;capacitor voltage balance

TM46

A

1003-3076(2014)12-0004-06

2014-03-11

国家电网公司大电网重大专项资助项目(SGCC-MPLG001-2012)

武晓堃(1990-)，男，河北籍，硕士研究生，研究方向为高压大功率变换器;李永东(1962-)，男，河北籍，教授，研究方向为高压大功率变换器与电机控制和调速。