油浸自冷式配电变压器换热特性的数值模拟研究

徐志明，吴凯，李秀云，柳青

(1．东北电力大学能源与动力工程学院，吉林省吉林市132012; 2．吉林省电力有限公司电力科学研究院，吉林长春130021; 3．中国水利电力物资有限公司，北京100045)

油浸自冷式配电变压器换热特性的数值模拟研究

徐志明1，吴凯1，李秀云2，柳青3

(1．东北电力大学能源与动力工程学院，吉林省吉林市132012; 2．吉林省电力有限公司电力科学研究院，吉林长春130021; 3．中国水利电力物资有限公司，北京100045)

为得到变压器设计者所关心的变压器内部绝缘油的速度分布和温度分布数据，运用FLUENT软件模拟油浸自冷式配电变压器内部换热特性。根据变压器实体数据，建立一个简化模型，采用RNG k-ε模型作为湍流模型，近壁处采用双层模型处理，得到了变压器内部绝缘油的速度和温度的分布情况，并与测量值进行对比分析，验证了数值模拟研究的正确性和可行性。数值模拟结果为油浸式配电变压器结构的优化设计与故障诊断提供了理论依据。

配电变压器;数值模拟;速度分布;温度分布

1 引言

油浸自冷式配电变压器在电力输配系统中应用广泛。变压器运行时，铁心、线圈和金属结构件均要损耗能量，这些损耗将转变为热量向外传递。这些热量被绝缘油吸收，通过油箱和散热设备散发到环境中去，从而达到热平衡。绕组的热点温度过高会影响变压器的寿命，甚至引发故障［1］。因此，对变压器换热特性进行研究分析很有必要。

目前，变压器换热特性的研究一般基于简单计算和试验测试。但是，由于试验误差过大，为了取得更为准确的数据，近几年，计算流体动力学软件在变压器换热特性计算分析领域得到了广泛应用。Oh and Ha利用低雷诺数湍流模型对单相圆柱式变压器油的自然对流传热分析求解［2］;Torrianoet等对干式变压器进行数值模拟，分析了不同模型、质量流量和进口边界条件对绕组温度分布情况的影响［3］;张海燕利用三维有限元方法，对变压器的温度场进行了分析和研究［4］。总体来看，关于变压器绕组温度场研究文献较多，但研究变压器内部整体流场及温度场分布情况的文献则少见于公开报道。

本文针对实际工程问题，选择一台额定容量为315kVA的油浸自冷式配电变压器为研究对象，利用FLUENT软件建立一个简化的三维流场和温度场数值模型，对此变压器换热特性进行数值模拟研究，得到了变压器内部绝缘油的速度和温度的分布情况。通过与实际测量数据的对比，验证了本文计算方法精度较高，为变压器热特性分析提供了一种分析方法，同时为研究油浸自冷式配电变压器冷却系统的优化改进与故障诊断提供了理论依据。

2 模型的建立

2.1 物理模型

本文以S9-M-315kVA/10kV配电变压器为研究对象，分析变压器内部流场和温度场的分布情况。该变压器的额定容量:315kVA;高压绕组电压等级: 10kV;低压绕组电压等级:0.4kV;额定频率:50Hz;冷却方式:油浸自冷(ONAN);油箱尺寸:900mm× 400mm×790mm;散热片尺寸:600mm×200mm;散热波纹板数量:54片。

变压器内部的主要构件为铁心和高、低压绕组。在变压器运行过程中，因铁心及绕组产生能量损耗引起变压器发热，变压器损耗包括空载损耗和负载损耗。此配电变压器的空载损耗:0.67kW;负载损耗:3.65kW。

根据变压器实体数据利用GAMBIT软件建立计算模型。为了有利于模拟计算，本文作出如下假设:

(1)暂忽略铁心和高、低压绕组内部的导热问题，即不建立油箱内部铁心和高、低压绕组模型。

(2)由于变压器构造非常复杂，并且在实际运行过程中，其流场呈对称分布，故取此变压器流场的1/2进行数值模拟，计算模型如图1所示。

图1 变压器计算模型Fig．1Solution model of transformer

为保证计算精度和收敛性，采用Hex六面体网格元素对散热片进行网格划分，采用Tgrid网格元素对油箱进行网格划分，网格总数为1108716。

2.2 控制方程

应用Reynolds时均方法的连续性方程式(1)、Navier-Stokes方程式(2)和能量方程式(3)求解［5］，其控制方程如下:

式中，u为速度;p为压力;x为坐标轴;i=1，2，3;j= 1，2，3;ρ为密度;μ为动力粘度;μT为湍流涡粘度; cp为比热;T为温度;λ为导热系数;λT为湍流热扩散率;k为湍动能;δij为克罗内克函数。

湍流模型选用RNG k-ε模型，RNG k-ε模型在湍流时均的连续性方程与雷诺方程的基础上，再建立一个湍动能的输运方程和一个湍流耗散率方程［6］，近壁处采用双层模型处理［7］，湍流涡旋、热扩散系数由式(4)和式(5)得出。

式中，经验常数Cv=100;PrT=0.85;ε为湍流耗散率。

2.3 边界条件

变压器绝缘油与外界的换热是一个综合了对流、导热、辐射换热的复合换热过程。本文暂忽略了铁心和绕组内部的导热问题，将铁心和绕组的外表面视为恒热流的自然对流传热。油箱及散热片外表面与外界空气之间的传热有两种:对流传热和辐射传热。所有壁面均按光滑无滑移平面处理，铁心和绕组产生的热量为整个变压器的1/2。油箱的几何形状比较规则，自然对流传热系数h可由下式得到［8］:

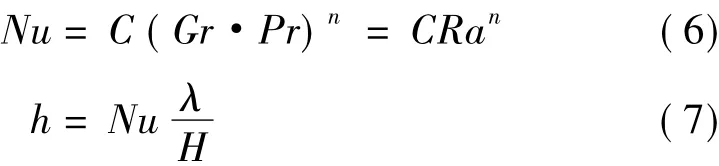
式中，Nu为努塞尔数;Ra为瑞利数;Gr为格拉晓夫数;Gr=(gaΔtH3)/v2;g为重力加速度;a为体积膨胀系数(单位:1/K);v为动力粘度(单位:m2/s);H为特征尺寸(单位:m);Δt为温差(单位:℃);Pr为普朗特数;C、n为试验确定的系数;λ为导热系数。

对于油箱盖:

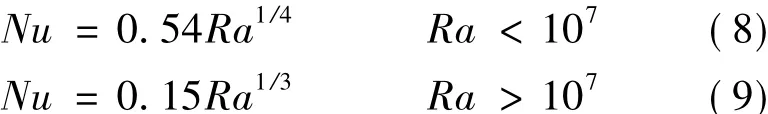
对于油箱底:

对于油箱竖直壁面及散热片:

本文模拟的是变压器内部自然油循环，油箱内部绝缘油是受浮升力驱动的自然对流问题。

考虑到变压器内绝缘油的各物性参数会随着温度变化，FLUENT软件模拟自然对流换热采用Boussinesq假设模型，变压器绝缘油的物性参数随温度变化如表1所示。

表1 变压器绝缘油的物性参数Tab．1Parameters of oil

辐射模型采用DO模型［9］，假定外界空气不参与辐射，油箱及散热片外表面为漫灰不透明表面，绝缘油在辐射传递过程中忽略散射。

3 结果与分析

3.1 模型正确性验证

为检验模型数值模拟计算结果的正确性，根据国家标准GB/T1094.7-2008的标准对变压器温度进行多点测量与监测，测量5组数据，取其平均值与计算值进行对比研究。由于条件所限，无法在变压器内部安装温度计，故测量如图2所示额定负载下的图中各点及周围环境的温度。

图2 测量点位置示意图Fig．2Position of measuring points

实验时，将低压输出端短路，通过改变高压端输入电流，模拟变压器不同负载。

两片散热片外表面测量点的温度分布情况基本相似，其中一片(A片)的测量温度和计算温度如表2所示。外界环境温度为300.2K。

通过与测量值的比较可以看出，计算误差均在5%以内，数值计算结果和测量值比较吻合。误差产生的原因如下:

(1)变压器实体模型的简化。

(2)变压器内部热源和热过程随运行条件而变化，具有不确定性。

结合测量数据和计算数据，可以推断出:变压器器身外表面的温度最高点位于散热片的顶部而不是油箱顶部，温度最低点位于油箱底部。

3.2 湍流模型验证

在油箱壁面附近由于分子粘性的阻尼作用，使湍流脉动逐渐削弱，需作相应的处理。本文采用RNG k-ε模型加近壁处的双层模型与Abid模型［10］、Launder-Sharma模型［11］以及Chang-Hsieh-Chen模型［12］三种低雷诺数k-ε湍流模型进行数值模拟，并进行对比。

表2 测量与计算温度值比较Tab．2Comparison of calculated and measured temperatures

经对比发现上述模型的变压器内部流场、温度场及油箱外表面的温度分布情况基本相似，RNG k-ε模型温度略高于其他模型，并且温度梯度表现明显，与测量结果更为相符。就油箱顶层油温而言，RNG k-ε模型分别比Abid模型、Launder-Sharma和Chang-Hsieh-Chen模型高1.3K、2.1K、1.8K，更为接近实验值。所以本文所选湍流模型较为合适。

3.3 数值模拟结果分析

本文模拟了油浸自冷式配电变压器在额定负载下的内部温度场和速度场。下面取此模型中最具代表性的平面进行分析。

如图3所示为环境温度为300.2K时z=0平面(图2中1～8点所构成的平面)的速度矢量分布情况。由图中可以看出:与文献［13］中的由于热偏差引起的流体单纯的上下流动不同，变压器绝缘油的流动受到绕组冷却通道吸力的影响。

在靠近铁芯上部竖直壁面和冷却油道的出口处产生了明显的上升羽流(A)，大部分油流上升到油箱顶部，由此处流入散热片并向下流动(B、C、D)。在图中E处，由于受到绕组冷却通道吸力的影响，油的流动分成两个部分，大部分油流回绕组冷却通道的出口(E)，其余部分继续向下流动(F)，进入油箱底部(H)和冷却通道入口(I)，形成一个自然循环回路。

速度分布图如图4所示。可以看出，变压器绝缘油的运动主要集中在油箱以及散热片的顶部，其最大流速可达0.022m/s。从散热片进入铁心、绕组冷却通道处的速度也是比较大的，油箱底部的速度基本可以忽略。

环境温度为300.2K时z=0平面的温度分布情况如图5所示。

图3 z=0平面速度矢量图Fig．3Results of velocity vectors of z=0

图4 z=0平面速度(m/s)分布Fig．4Velocity(in m/s)distribution of z=0

从温度分布图中可以看出变压器油箱、散热片内竖直方向油的温度梯度分布尤为明显，但水平方向温度梯度并不明显。油箱顶层油温最高:352K，油箱底部油温最低:330K。铁心、绕组将附近的油加热，油的温度逐渐上升，热油的流速增大，高温热油迫使周围的油向上流动，通过油箱盖与外界换热后，进入散热片，与外界发生热量交换后，油温降低，冷油填补高温油的空缺，继续吸收绕组、铁心散发的热量，形成自然循环冷却。

图5 z=0平面温度(K)分布Fig．5Temperature(in K)distribution of z=0

结合油的速度矢量图可知，油在散热片内特殊的流动将会影响其内部油的温度分布。图5中，散热片内上部(区域1处)油温几乎保持不变，在区域2处油温开始慢慢下降，在区域3处油温急剧下降。

4 结论

(1)模拟计算得到了油浸自冷式配电变压器内部绝缘油流场和温度场的分布情况，验证了数值模拟结果的有效性，为研究变压器冷却系统的优化改进与故障诊断提供了理论依据。

(2)变压器器身外表面的温度最高点位于散热片的顶部而不是油箱顶部，温度最低点位于油箱底部。

(3)受绕组冷却通道吸力的影响，绝缘油的流动方式与一般的恒热流加热方腔内流体的流动方式不同。变压器内部绝缘油热分层现象与其流动方式有关。

［1］辜承林，朱建华(Gu Chenglin，Zhu Jianhua)．电力主设备制造与运行监测新技术(New manufacture operation and monitoring technologies of electric apparatus)［J］．电力自动化设备(Electric Power Automation E-quipment)，2004，24(7):19-30．

［2］K J Oh，S S Ha．Numerical calculation of turbulent natural convection in a cylindrical transformer enclosure［J］．Heat Transfer-Asian Research，1999，28(6):429-441．

［3］F Torriano，M Chaaban，P Picher．Numerical study of parameters affecting the temperature distribution in a disctype transformer winding［J］．Applied Thermal Engineering，2010，30(14-15):2034-2044．

［4］张海燕，储晨昀，李元媛(Zhang Haiyan，Chu Chenyun，Li Yuanyuan)．变压器温度场的有限元分析(Fi-nite element analysis of temperature field in transformer)［J］．变压器(Transformer)，2011，48(3):25-28．

［5］陶文铨(Tao Wenquan)．数值传热学(Numerical heat transfer)［M］．西安:西安交通大学出版社(Xi’an: Xi’an Jiaotong University Press)，2001．

［6］Yakhot V，Orszag S A．Renormalization group analysis of turbulence．I．Basic theory［J］．Journal of Scientific Computing，1986，1(1):3-51．

［7］T Jongen，Y P Marx．Design of an unconditionally stable positive scheme for the k-ε and two-layer turbulence models［J］．Computers and Fluids，1997，26(5):469-487．

［8］弗兰克P．英克鲁佩勒，大卫P．德维特，狄奥多尔L．伯格曼，等(F P Incropera，D P De Witt，T L Bergman，et al．)．传热和传质基本原理(原著第6版) (Fundamentals of heat and mass transfer，sixth edition)［M］．葛新石，叶宏(Ge Xinshi，Ye Hong)，译．北京:化学工业出版社(Beijing:Chemical Industry Press)，2007．

［9］G D Raithby，E H Chui．Afnite volume method for predicting a radiant heat transfer in enclosures with participating media［J］．Journal of Heat Transfer，1990，112 (2):415-423．

［10］Abid R．Evaluation of two-equation turbulence models for predicting transitional flows［J］．International Journal of Engineering Science，1993，31(6):831-840．

［11］N Z Ince，B E Launder．On the computation of buoyancydriven turbulent flows in rectangular enclosures［J］．International Journal of Heat and Fluid Flow，1989，10 (2):110-117．

［12］K C Chang，W D Hsieh，C S Chen．A modified low-Reynolds-number turbulence model applicable to recirculating flow in pipe expansion［J］．ASME Journal of Fluids Engineering，1995，117(3):417-423．

［13］杨沫，李少华，徐志明，等(Yang Mo，Li Shaohua，Xu Zhiming，et al．)．三维方腔内竖直平板自然对流的数值模拟(Numerical simulations of three-dimensional natural convection in an enclosure with an internal isolated vertical plate)［J］．工程热物理学报(Journal of Engineering Thermophysics)，1996，17(2):209-212．

Numerical modeling of heat transfer performance of ONAN distribution transformers

XU Zhi-ming1，WU Kai1，LI Xiu-yun2，LIU Qing3
(1．Energy and Power Engineering Institute，Northeast Dianli University，Jilin 132012，China; 2．EPRI of Jilin Electric Power Co．Ltd．，Changchun 130021，China;3．China National Water Resources＆Electric Power Materials＆Equipment Co．Ltd．，Beijing 100045，China)

The thermal behaviour of ONAN distribution transformers has been numerically modeled using FLUENT for obtaining the velocity distribution and temperature distribution of insulating oil．A simplified model has been developed according to the transformer entity data．Turbulence was modeled using the RNG k-ε turbulence model，while 2-layer approach was adopted to deal with turbulence near the wall．The insulating oil flow and the thermal distribution results inside transformer were presented．The devised model has been validated by comparing the numerical results with the experimental ones．The conclusion provides theory basis for optimization design and fault diagnosis of ONAN distribution transformers．

distribution transformer;numerical modeling;velocity distribution;temperature distribution

TM421

A

1003-3076(2014)12-0041-05

2012-11-01

徐志明(1959-)，男，吉林籍，教授，博士，研究方向为节能理论与技术、换热设备的污垢和强化换热;吴凯(1986-)，男，河北籍，硕士研究生，研究方向为节能理论与技术。