脚掌转动对腿型机器人起跳影响的研究
王茂林,孙天仕,高爽
哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001
如今,跳跃机器人因优秀的避障能力和非结构性复杂环境的适应能力,越来越吸引研究者的目光和研究兴趣[1]。其中带脚掌腿型跳跃机器人更是因既可动态连续跳跃又可单次跳跃或间隔跳跃的特点,以及较高的仿人度发展尤其迅速。东京工业大学的Masaki Yamakita等研究了仿猫型的腿型机器人,能够通过蹬墙壁实现较高的跳跃[2]。日本庆应义塾大学的Eijiro Ohashi使用腿型跳跃机器人实现了跳跃高度的控制[3]。但是很多研究中都未考虑脚掌转动对跳跃的影响。例如杨煜普教授等研究的翻转跳跃运动机器人,就是典型的带脚掌的腿型跳跃机器人,但是该研究中没有考虑脚掌围绕脚尖的转动[4]。一些研究也考虑了脚掌转动的情况,如日本东北大学的Sang⁃Ho Hyon等研制的四连杆平面体操机器人在动力学建模时就考虑了脚掌的转动,但对脚掌的转动对机器人的影响没有阐述[5]。文中就带脚掌腿型机器人在脚掌转动与脚掌不转动两种情况进行对比研究,阐明脚掌欠驱动即脚掌转动对起跳离地前这段跳跃过程的影响。
1 带脚掌腿型机器人结构
图1中展示了带脚掌腿型跳跃机器人的实物模型及其简化模型。机器人由脚掌、小腿和大腿组成。踝关节和膝关节分别由直流伺服电机驱动。连杆的质量为mi(i=0,1,2),围绕质心的惯量为Ii。 2 个主动关节分别对应广义坐标θ2、θ1。起跳离地前,脚掌在两电机动作下若产生围绕脚尖的欠驱动转动,则此转动的角度定义为θ0。所以定义机器人系统的广义坐标为θ2、θ1、θ0。 模型总质心为(xc,yc)。

图1 腿型机器人模型图片和其简化模型
2 脚掌不转动起跳与脚掌转动起跳
在脚掌转动情况下,机器人从初始时刻t1开始到t2时刻机器人关节弯曲实现下蹲,这一过程中脚掌与地面始终接触且不滑动,称为站立相。然后关节伸展达到t3时刻的起跳离地姿态。这一过程脚掌围绕脚尖转动且脚尖不滑动,称为欠驱动相[6],如图2所示。

图2 脚掌转动时的起跳序列
图3展示了在脚掌不转动情况下,机器人从静止到起跳离地前的起跳序列。因为文中研究脚掌转动与否对起跳离地前这段跳跃的影响,所以规定其从开始到起跳离地与脚掌转动耗时相同,均为t1到t3。此过程从初始时刻t1开始,机器人关节弯曲实现下蹲动作,然后关节伸展达到t3时刻的起跳离地姿态。起跳时脚掌水平地抬离地面,这一过程中脚掌始终与地面接触,脚掌没有转动现象。

图3 脚掌不转动时的起跳序列
3 腿型机器人动力学分析
脚掌不转动时只有θ2、θ1这2个广义坐标,脚掌转动时有3个广义坐标θ0、θ1、θ2。 虽然两种情况下广义坐标数目不同,但是脚掌转动情况下令θ0=0即可适用于脚掌不转动情况,因此选用广义坐标为q=[θ0,θ1,θ2]T。 运动拉格朗日动力学方程得到机器人的动力学方程描述:

上述方程中τ=[0,τ1,τ2]T。 踝关节和膝关节力矩分别为τ1和τ2。F=[Fx,Fy]T是表示机器人受到地面的水平摩擦力和垂直反力。方程中惯性矩阵D3×3与科氏矩阵C3×3均为对称矩阵。
4 起跳过程中的约束
4.1 脚掌不转动情况的起跳约束
(2)起跳时脚掌与地面之间没有相对滑动,所以有:
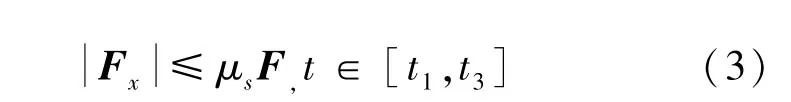
其中μs是静摩擦力系数。
由ZMP稳定性理论知机器人与地面的力必须作用于脚掌的支撑区域中。因而有约束:
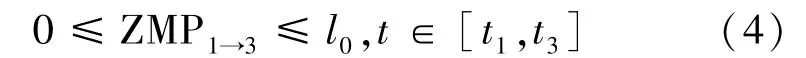
水平方向ZMP的坐标求解公式为
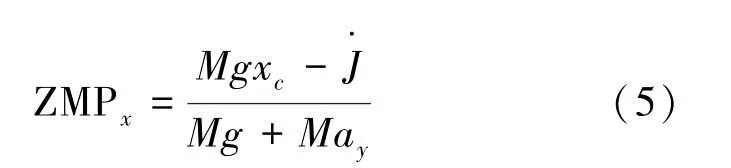
其中M为总质量,xc为总质心的x方向坐标,ay为总质心在铅垂向的加速度,为围绕脚掌处的角动量的微分[7]。
(3)要求质心CoM的起跳方向,即:
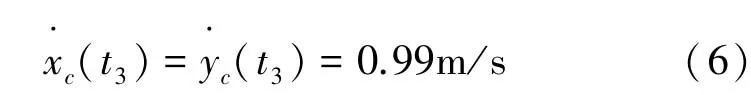
(4)受到电机机械特性约束为
其中ki是电机转矩常数,ke是速度常数,n为减速器减速比,R是电机线圈电阻,U是输入的电压。
4.2 脚掌转动情况的起跳约束
前面讲述了脚掌不转动起跳的约束条件。这里对脚掌转动起跳与脚掌不转动起跳的异同做出说明。
相同点:初始姿态的约束(1)、地面作用力约束(2)、起跳方向约束(3)以及电机机械特性的约束(4)对脚掌转动方式起跳都适用。
不同点:因脚掌转动,所以约束(2)、(3)和(4)计算时需要计入θ0(t)的影响。
用算符Γ代表θ0和θ1、θ2的函数关系,表示为
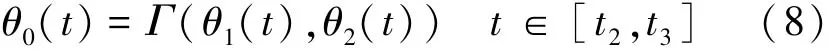
方程(8)可以由动力学方程解耦获得[8]。
5 关节的轨迹规划
两种起跳方式的轨迹规划方式是相同的,均以电机能耗最小为优化目标,所以对脚掌转动与不转动时起跳的轨迹解算做统一阐述。因为电机的能耗与电流平方成一定比例关系,而电流与电机力矩又成一定线性关系,所以能耗定义为:
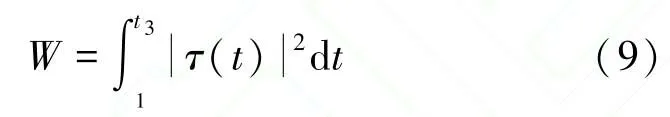
关节轨迹θ1(t)、θ2(t) 用五阶多项式来描述为:
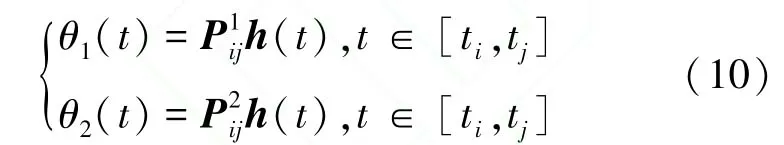
其中(i,j)= (1,2),(2,3),h(t)= [1t t2…t5]T。 由动力学方程(1)可以解算
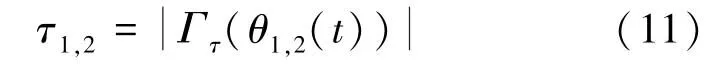
将式(11)带入式(9)中即可得到优化目标[9]。
6 仿真和实验
机器人结构参数示意图和部分参数如图4和表1所示。
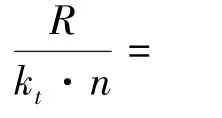

图4 机器人结构参数示意图
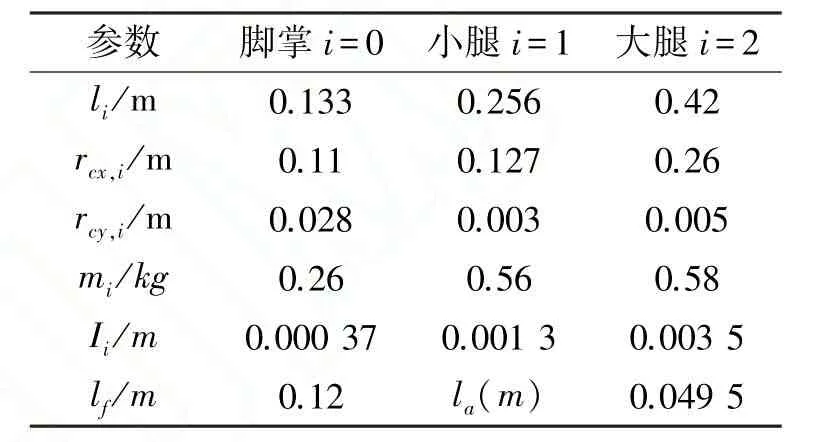
表1 机器人结构参数
6.1 脚掌不转动情况下的仿真和实验结果

机器人在脚掌不转动情况下起跳的仿真时序图如图5(a)所示,质心的时序图如图5(b)所示。根据图5(a)得知,机器人先下蹲,然后快速站起,达到起跳效果。由图5(b)得知确实没有满足起跳角45°的约束,优化的最小起跳角度为56°左右。


图5 脚掌不转动起跳仿真
将以上仿真结果应用于实验,脚掌不转动起跳时的实验结果展示如图6所示。

图6 脚掌不转动起跳实验图片
脚掌不转动情况下起跳的踝关节电机和膝关节电机的力矩曲线如图7所示,从中可以看到电机不仅在质心由低抬高时力矩较大,而且在机器人下蹲,质心下降时也需要较大的力矩。根据式(9)可知,在整个起跳过程中对图7中两个关节的力矩进行平方再积分,可以得到的能耗为W=3.31(N2·m2·t)。
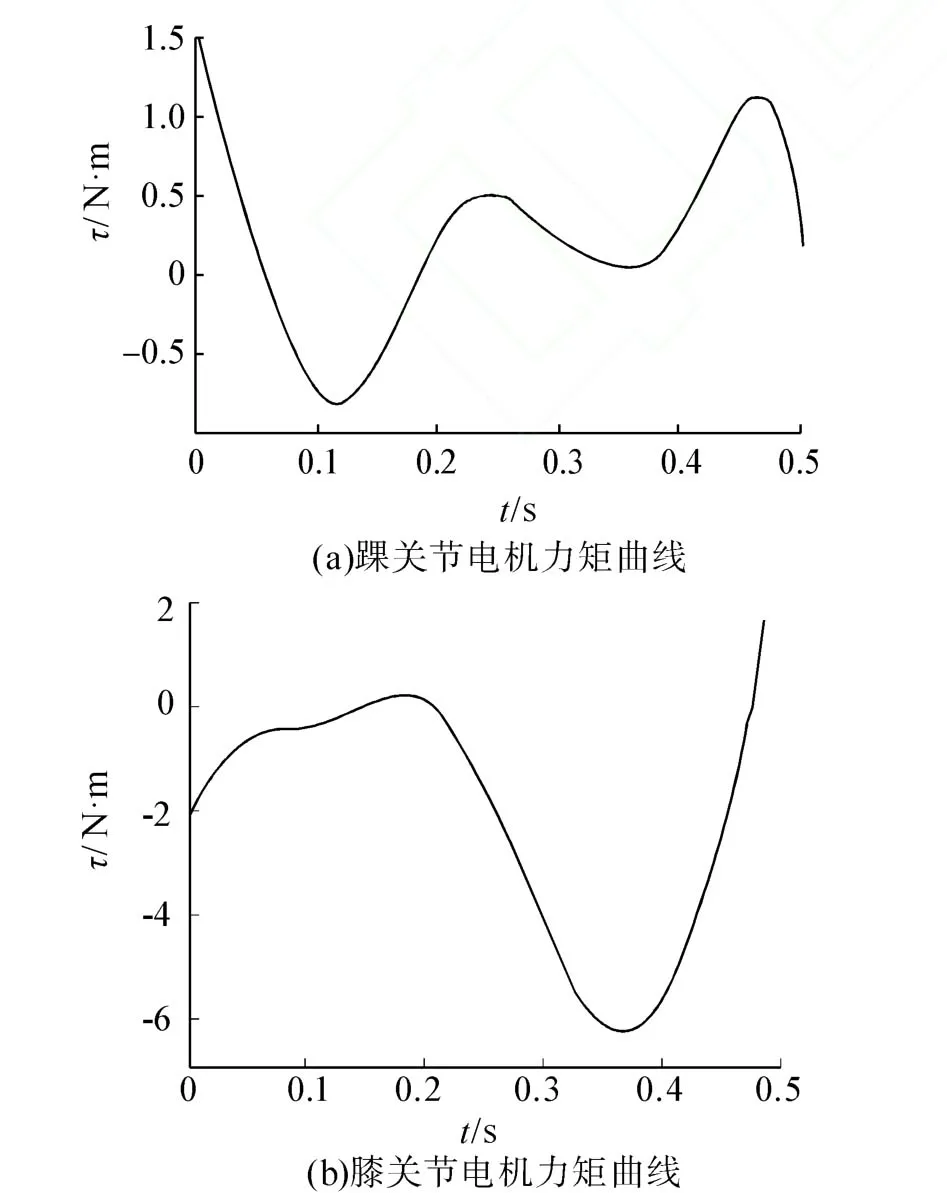
图7 脚掌不转动起跳关节力矩曲线
6.2 脚掌转动情况下的仿真和实验结果
机器人在脚掌转动情况下起跳的仿真时序图如图8(a)所示,质心的时序图如图8(b)所示。根据图8(a)得知机器人先下蹲,此时机器人开始围绕脚尖转动,然后快速站起,达到起跳效果。由图8(b)知机器人起跳角度为45°。
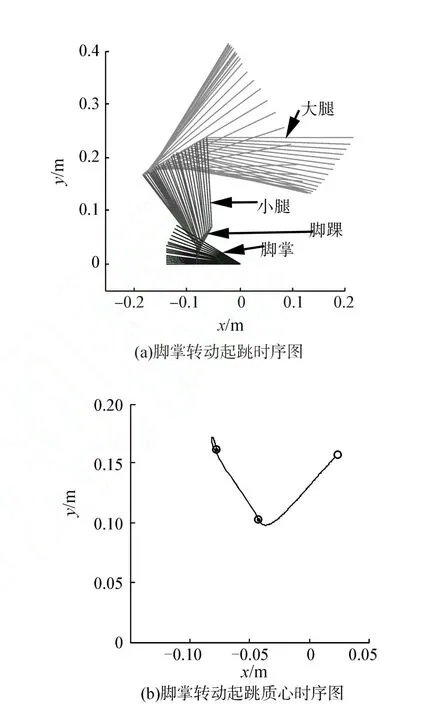
图8 脚掌转动起跳仿真
将以上仿真结果应用于实验,脚掌转动起跳时的实验结果如图9所示。

图9 脚掌转动起跳实验图片
脚掌转动情况下起跳的踝关节电机和膝关节电机的力矩曲线如图10所示,从中可知在机器人下蹲时力矩曲线相对平缓,能耗较少。在质心抬升,机器人向上起跳时,膝关节和踝关节电机快速动作,此时消耗了机器人脚掌转动起跳时的大部分能量。根据式(9)可知,在整个起跳过程中对图10中两个关节力矩进行平方再积分,仿真得到整个起跳过程的能耗为W=1.25(N2·m2·t)。

图10 脚掌转动起跳关节力矩曲线
脚掌转动情况下起跳的踝关节电机和膝关节电机的力矩曲线如图10所示,从中可知在机器人下蹲时力矩曲线相对平缓,能耗较少。在质心抬升,机器人向上起跳时,膝关节和踝关节电机快速动作,此时消耗了机器人脚掌转动起跳时的大部分能量。根据式(9)可知,在整个起跳过程中对图10中两个关节力矩进行平方再积分,仿真得到整个起跳过程的能耗为W=1.25(N2·m2·t)。
4 结束语
文中制作了一款带脚掌的腿型机器人,建立了机器人在脚掌转动与不转动两种情况下起跳时的动力学方程,分析了两种情况下的起跳约束。以电机能耗最小为优化目标,对两种情况起跳进行轨迹优化。使用实际模型数据分析,仿真得到了两种情况下在起跳时的时序图、总质心时序图、力矩曲线以及能耗值。仿真结果表明:带脚掌的腿型机器人起跳时脚掌转动比脚掌不转动消耗的能量少,而且起跳角度范围也更宽。
[1]徐兆红.腿式跳跃机器人运动规划与稳定性恢复研究[D].上海:上海交通大学,2009:2⁃20.
[2]MASAKI Y, YASUHITO O, YASUAKI T.Jumping cat ro⁃bot with kicking a wall[J].Journal of the Robottics Society of Japan, 1994, 9(6): 934⁃938.
[3]EIJIRO O, KOUHEI O.Hopping height control for hopping robots[J].Electrical Engineering in Japan.2006, 155(1):64⁃71.
[4]杨煜普,耿涛,郭毓.一种新型翻转跳跃运动机器人的运动结构与轨迹规划[J].上海交通大学学报,2007,37(7): 1110⁃1113.
[5]SANG H H, EMURA T.Quasi⁃periodic gaits of passive onelegged hopper[C] //Proceedings of the 2002 IEEE /RS J International Conference on Intelligent Robots and Systems.Piscataway, USA: IEEE, 2002, 2625⁃2630.
[6]WU Tingying, YEH T J, HSU BingHung.Trajectory Plan⁃ning of a one-legged robot performing stable hop[C]//In⁃ternational Conference on Intelligent Robots and Systems.Taipei, China, 2010, 4922⁃4927.
[7]梶田秀司.仿人机器人[M].北京:清华大学出版社,2007: 61⁃90.
[8]薛定宇,陈阳泉.高等应用数学问题的 MATLAB求解[M].2 版.北京:清华大学出版社,2008: 184-185,220⁃234.
[9]黄孝亮.一类欠驱动步行机器人运动学动力学分析及控制算法研究[D].长春:吉林大学,2009:10⁃20.

