双螺杆泵螺杆成型铣刀廓形设计与研究
杨妙妙,董黎敏,王 建,史津平,郭津津
(天津理工大学复杂系统控制理论及应用重点实验室,天津300384)
0 前言
双螺杆泵的核心部件是一对螺杆转子,转子的螺旋头数通常有单头和双头两种[1]。双螺杆泵螺杆转子的型线由点、直线及多段曲线组合而成,目前一般采用无瞬心包络法设计盘形铣刀,用盘形铣刀加工螺杆转子时,刀具轴线与转子轴线空间交错,两者有一夹角,盘形铣刀绕其中心轴旋转,转子坯轴绕轴心线旋转并沿轴向移动,盘形铣刀与转子坯轴所形成的复合运动的结果是剔除了转子坯轴的多余材料而形成所要得到的螺旋曲面[2]。本文基于对双头双螺杆泵螺杆形状的分析建立了螺杆螺旋曲面方程;利用成形铣削原理和坐标变换理论,从成形铣刀与螺杆工件的相对运动关系出发,建立了基本的铣刀刀刃廓形方程。在设计刀具的过程中,不可避免需要求解隐函数和三角超越方程等复杂的关系式。文中给出了刀具型面计算式的推导过程及应用 Matlab软件对设计刀具过程中的复杂数学关系式求解的方法;并给出以具体型线为实例的计算数据。该方法是实现螺杆型面铣削刀具设计的快速准确求解计算的一种有效方法。
1 成形铣削原理
当在专用铣床上加工螺旋面时,工件以螺旋参数作螺旋运动,而铣刀则绕着自身的轴线作旋转切削运动。所以螺旋槽是在刀具回转面与工件的相对运动作用下形成的。用成形铣刀加工螺杆螺旋槽时刀具和工件的相对位置如图1所示。
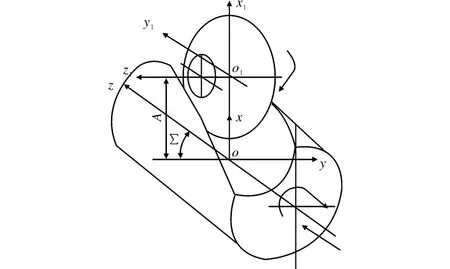
图1 刀具与工件相对位置Fig.1 Relative position of cutter and workpiece
铣刀廓形和刀具与工件的相对位置决定螺旋槽的形状。如果以工件为参照物,此时刀具绕着工件的轴线作螺旋运动,则工件上的螺旋面是刀具回转面所形成的包络面。如果把螺旋面看成是一系列导程相同的螺旋线,而铣刀为一系列半径不同的铣刀圆,则螺旋面的一条螺旋线就是由铣刀上的一个铣刀圆切削形成的,如图2所示。

图2 铣刀圆的包络线Fig.2 Envelope of milling cutter
在加工过程中,已加工出的螺旋面与铣刀的回转面之间始终存在一条相切于两个面的空间曲线,称为接触线。铣刀廓形计算的关键就是求解此接触线。
2 铣刀廓形计算
2.1 齿形与齿面方程式
在端平面上的齿形,如果沿其轴向移动并绕轴线旋转的话,即可得到转子的齿面螺旋曲面。转子齿形型线的方程式为

式中,t为齿曲线参数。
由式(1)可以得到螺旋曲面的方程,即齿面方程为

式中,θ为角度参数,表示母线绕z轴转过的角度,顺着z轴看,以顺时针方向转动为正;P为螺旋参数,P=T/2π,表示母线绕着z轴转过单位角度时,在轴线方向上移动的距离。
2.2 刀具与工件坐标转换
为了便于推导接触方程,根据工件与成形铣刀的相对位置关系建立直角右手坐标系,如图3所示。在工件上建立坐标系o-xyz,使其z轴与工件的轴线重合。在刀具上建立坐标系o1-x1y1z1,z1轴与刀具的轴线重合。x轴与x1轴重合,且方向一致。以上两个坐标系是固定的,不随工件和刀具运动。设两坐标系原点之间的距离为A,z轴与z1轴之间的夹角为Σ。

图3 坐标系关系图Fig.3 Relative between coordinate systems
由图3可知,从o坐标系到o1坐标系的转换式为

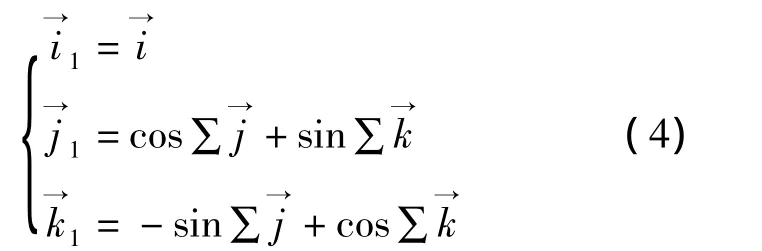
2.3 接触条件式
由于两曲面相切接触,根据空间解析几何知识与运动学原理,刀具回转面与工件螺旋面的接触点处,两个曲面的公法线矢量与相对运动的速度矢量垂直,可得接触条件

如图4所示,M(x,y,z)为两曲面接触线上的一点,则M点相对于两坐标系原点的矢径为
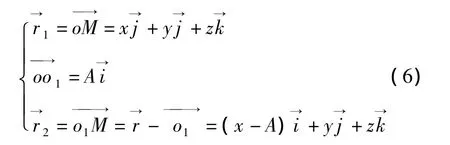
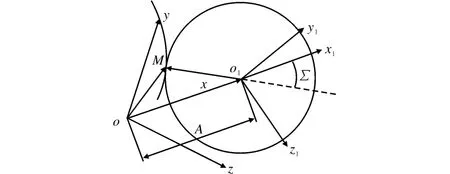
图4 接触点处径矢示意图Fig.4 Radius vector of contact point

将式(6)带入式(7),得

M点随刀具运动的线速度v2为

将式(4)和式(6)带入式(9),得

由接触条件式(5)可知
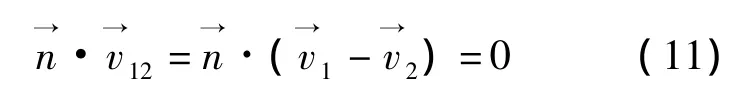
由微分几何的知识可知,曲面上任意一点M(x,y,z)的法线矢量可以表示为
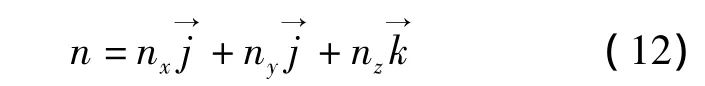
式中,nx、ny、nz分别是曲面法线矢量的各轴分量。

由式(13)可推算出螺旋面的特征方程

该方程是螺旋曲面的一个重要性质,表示螺旋面上任意一点处坐标(x,y,z)与该点处法线的各轴分量(nx,ny,nz)及螺旋参数P之间的关系。
将式(7)、式(9)和式(13)代入式(11),并通过螺旋面的特征方程式(14)得接触方程为

式中,A、Σ和P都是常数,而其它值是关于参变数t和θ的函数,因此接触方程是关于t和θ的方程。“+”号表示右旋,“-”表示左旋。
接触条件式表示螺旋面与铣刀回转面相切接触的关系,通过解此方程得到的是螺旋槽端面廓形上的点成为接触点时工件所转过的角度θ。方程中只有一个未知数,但它是超越方程的形式,本文选择牛顿迭代法对接触条件式进行求解。
2.4 铣刀回转面廓形求解
将工件端面型线的坐标点数据(x0,y0,z0),与各点处一阶导数代入到接触方程式(15),可求得工件端面上各点成为接触点时需要转过的角度θ;然后将坐标值(x0,y0,z0)与此点处的旋转角θ代入螺旋面方程式(2),可以得到螺旋面上接触点的坐标(x,y,z)。因为要求刀具的廓形,将一系列接触点代入到坐标系变换式(3),得到接触点在刀具坐标系内的坐标(x1,y1,z1);最后由刀具廓形方程式(16)求得刀具回转面的径向截形。

3 基于Matlab的计算
3.1 螺杆型线曲线组成
如图5所示,本文螺杆型线由ab、bc、cd、de、ef、fg、gh、hi、ij、jk、kl、la 等 12 段曲线组成,其中,ab段是从b点开始沿顺时针方向滚动形成的普通外摆线;bc段是以齿顶圆半径为摆径从b点开始沿逆时针方向滚动形成的长幅外摆线。利用Pro/E绘制出转子三维啮合图如图6所示。
3.2 Matlab求解方程
Matlab作为一款功能强大的计算平台,现在已经成为最为普遍的科学计算工具之一。本文利用其独特优势,实现了对各方程的求解,以达到快速准确地求出结果的目的。

图5 螺杆端面型线Fig.5 Profile of screw end face

图6 转子3D立体啮合图Fig.6 3D drawing of rotor mesh
在用Matlab编制的程序求解接触方程时,需要先使用ez-plot画出扭转角θ和型线参数t之间的t-θ关系图,以ab摆线为例,得到t-θ关系,如图7所示,在(-2π,2π)内,横坐标t值对应多个θ值,所以依据R最小原则,依图选适当的迭代初值θ0。

图7 ab摆线型线参数t与扭转角θ关系图Fig.7 Relationship between the profile parameter t and the torsion angle θ of cycloid ab
通过Matlab程序计算将得到包含一系列离散的刀具刃形点(Ri,Zi)。利用Matlab编程绘制出刀具廓形图,如图8所示。方便进一步利用Pro-E准确地绘制出刀具的三维模型图。

图8 阴、阳转子刀具廓形图Fig.8 Profiles of the male and female rotor cutters
4 结论
由于螺杆成形铣刀设计计算过程中涉及到隐函数和三角函数等非线性方程,在实际应用中求解方程较为复杂且耗时,直接影响刀具设计的精度和效率。通过建立螺杆螺旋曲面方程,再利用成形铣削基本原理和坐标变换理论,推导出铣刀刀刃廓形方程。利用了Matlab的科学计算优势,编制程序完成刀具的设计计算过程,保证了刀具设计的准确性。
[1]李继峰,郑青春,郭津津,等.双螺杆泵双头螺旋型线分析及其对流量影响[J].重型机械,2013(1):55-58.
[2]王小明,罗芝华,杨志,等.基于Matlab的双螺杆压缩机转子盘形铣刀数字化设计方法[J].机床与液压,2012,40(15):84-86,114.
[3]李成松.加工螺旋曲面的盘形铣刀设计系统开发[D].哈尔滨工业大学,2011.
[4]赵春秀,刘建宁.螺杆加工成型铣刀廓形坐标计算方法[J].机械设计,2008(6):69-70.
[5]王正林,龚纯,何倩.精通MATLAB科学计算[M].北京:电子工业出版社,2009.
[6]宋超,殷国富.基于运动原理计算加工螺旋槽用成型盘铣刀刀具廓型线方法研究[J].工具技术,2010,44(8):58-61.
[7]赵海晖,孟垂成.基于虚拟现实的螺杆泵设计与仿真[J].石油矿场机械,2007(08).
[8]陈明战,曹刚,孙新艳,等.螺杆泵水力特性检测曲线推导及应用[J].石油矿场机械,2012(11).

