腐蚀海洋立管剩余强度预测*
俞树荣 王 超
(兰州理工大学石油化工学院)
海洋立管是海洋平台与海底井口间的主要连接件,是海洋油气资源运输中的薄弱环节,在内部输送介质和外部环境的共同作用下,极易发生腐蚀损伤。海洋立管发生腐蚀后,其剩余强度和承载能力下降,检测和维修费用上升,维修和更换周期缩短,投资和运行费用增加,整个输送系统的正常运行将受到干扰[1]。因此,必须对在役的海洋立管进行合理的剩余强度评估以保证其安全运行。
20世纪70年代以来,国际上逐步发展形成了具有安全可靠性和经济性的剩余强度评价方法,其中美国的ASME B31G[2]和API579[3]、英国的BS7910[4]、挪威的DNV-RP-F101[5]与加拿大的CAS-Z184-M86[6]相对具有代表性,但这些方法是各国在特定的试验环境中得到的,因此都有一定的使用条件和应用范围。近年来,关于人工神经网络在腐蚀管道剩余强度评价方面的应用得到了广泛关注。笔者将遗传算法与人工神经网络相结合,有效地解决了人工神经网络自身的局限性,从而能更加科学、有效地对在役腐蚀海洋立管的剩余强度进行预测。
1 DNV-RP-F101评价标准
DNV-RP-F101标准是由英国燃气公司(BG)和挪威船级社(DNV)于1999年联合颁布的管道腐蚀标准[6]。该标准提供了两种安全准则不同的腐蚀缺陷评价方法,即分项安全系数法和许用应力法。分项安全系数法的计算过程和测定要相对复杂,而许用应力法主要侧重于现场应用,相对简明、便捷。因此,笔者采用许用应力法对含单个腐蚀缺陷海洋立管的剩余强度进行计算。
许用应力法需要先计算出具有腐蚀缺陷管道的失效压力(即剩余强度),然后再将该失效压力乘以一个基于初始设计参数的单一安全系数而得到最终的安全工作压力。
仅有内压荷载的单个缺陷的安全工作压力和腐蚀管道失效压力的计算公式为:
psw=Fpf
式中d——腐蚀缺陷深度,mm;
D——管道直径,mm;
F——管道强度设计系数;
l——腐蚀缺陷长度,mm;
pf——腐蚀管道失效压力,MPa;
psw——腐蚀管道安全工作压力,MPa;
Q——长度修正因数;
t——管道壁厚,mm;
UTS——比例极限强度,MPa。
2 GA-BP神经网络模型
人工神经网络是指由大量人工神经元互连而成的非线性自适应动力系统,是一种旨在模仿人脑结构及其功能的信息处理系统。它具有自组织、自学习和非线性映射的能力[7]。目前,BP神经网络是研究最为成熟、应用最为广泛的人工神经网络模型之一。但由于BP算法属于误差梯度下降算法,在进行全局搜索时,不可避免地存在收敛速度慢、易出现“平台效应”以及陷入局部极小点等缺点[8]。而遗传算法是基于自然界中生物自然选择和遗传规律的并行搜索算法,是目前理论上最成熟、运用最广、效果最好和最有发展前景的全局搜索方法。因此,笔者利用遗传算法优化BP神经网络(简称GA-BP神经网络)的权值和阈值来改进BP神经网络的性能,以克服局部极小值,实现全局收敛,提高学习精度、泛化能力和网络的稳定性。
2.1 BP神经网络模型的构建
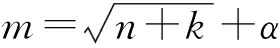

图1 BP神经网络模型示意图
2.2 GA-BP神经网络的权值和阈值
GA-BP神经网络流程如图2所示。
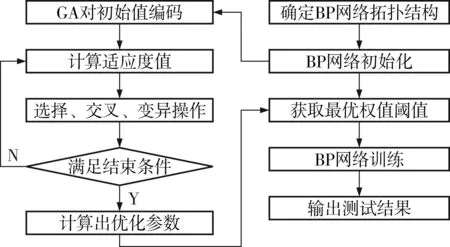
图2 GA-BP神经网络流程
GA-BP神经网络的具体操作过程如下:
a. 编码。为扩大搜索空间,保证网络权值和阈值的高精度,笔者采用实数编码。将BP神经网络的权值和阈值级连起来,形成一个实数组,作为遗传算法的一个染色体。编码长度即染色体的长度S=n×m+m×k+m+k。
b. 确定适应度函数。采用神经网络的目标函数(Ei)取其倒数作为染色体的适应度函数(Fi)。
c. 选择操作。选择操作是指从旧群体中以一定概率选择个体到新群体中,个体被选中的概率跟适应度值有关,个体适应度值越好,被选中的概率越大。笔者采用一种回放式随机采样方法——轮盘赌法。
d. 交叉操作。交叉操作是指以一定交叉概率在种群中随机选择互相配对的两个染色体,将其部分结构替换重组,从而形成新的个体。由于个体采用实数编码,所以交叉操作方法采用实数交叉法。
e. 变异操作。遗传算法引入变异操作可以提供初始种群不含的基因,或找回选择操作中丢失的基因,为种群提供新的内容。变异操作一方面能使遗传算法具有局部的随机搜索能力,在接近最优解的领域时加速向最优解收敛;另一方面能维持种群多样性,防止出现不成熟收敛。因此,笔者采用均匀变异。
f. 将新个体插入到种群中去,并计算出新个体适应度值。
g. 用最优的权值和阈值作为BP神经网络的初始条件,对BP神经网络进行训练。
创刊于1946年的《文联》,共发表了121篇文章,文类体裁多样,主题丰富,在不同程度反映了社会的整体面貌:有歌颂战争期间兵民的团结一心、众志成城;有揭露站前战后黑暗腐败的现实和专制独裁的野心;有批判具有劣根性的国民;有鞭挞帝国主义的狼子野心;也有讴歌光明的赞歌等,具有强烈的时代感。由于年代的限定,《文联》是存在缺陷的,像存在对文化市场的迎合,满足底层市民的消极趣味。但不可否认《文联》对于先进思想的传播,对于先进文化的弘扬以及对于文艺创作的繁荣,都产生了积极深远的影响,在现代文学报刊史上留下了浓墨重彩的画卷。
适应度函数的表达式为:
式中Ei——误差平方和;
Fi——i的适应度值;
m——输出层节点数;
oj——期望值;
tj——输出层输出值。
3 预测实例
3.1 BP神经网络和GA-BP神经网络的建立
3.2 BP神经网络和GA-BP神经网络的训练
采用BP神经网络和GA-BP神经网络模型,对网络进行训练,其误差随训练次数变化曲线如图3所示,目标误差设定为0.000 1,BP神经网络经过194次训练后可以达到训练目标,而GA-BP神经网络只需要17次就能达到训练目标。由此看见,GA-BP神经网络模型可有效地提高网络的收敛速度。

图3 训练后误差变化曲线
3.3 BP神经网络和GA-BP神经网络的预测
应用上述两种训练好的网络对测试集样本进行测试。为能说明网络预测的准确性,选取测试集样本进行测试并与DNV-RP-F101标准计算结果进行比较,预测结果如图4所示。
从图4a可以看出,两种神经网络的预测值曲线都与DNV-RP-F101计算值曲线很好地吻合。但经放大后比较可以发现,图4b、c中GA-BP神经网络模型具有更好的预测效果,可以更好地预测腐蚀海洋立管的剩余强度。
在图4a中,A、B处分别是BP神经网络和GA-BP神经网络预测相对误差的最大值点,图4b、c是两处的放大。可以看出,采用BP神经网络预测其相对误差的最大值发生在17点处,最大相对误差为5.38%,而采用GA-BP神经网络预测其相对误差的最大值发生在12点,最大相对误差为1.99%。通过最大相对误差比较可知,GA-BP神经网络具有较高的预测精度。
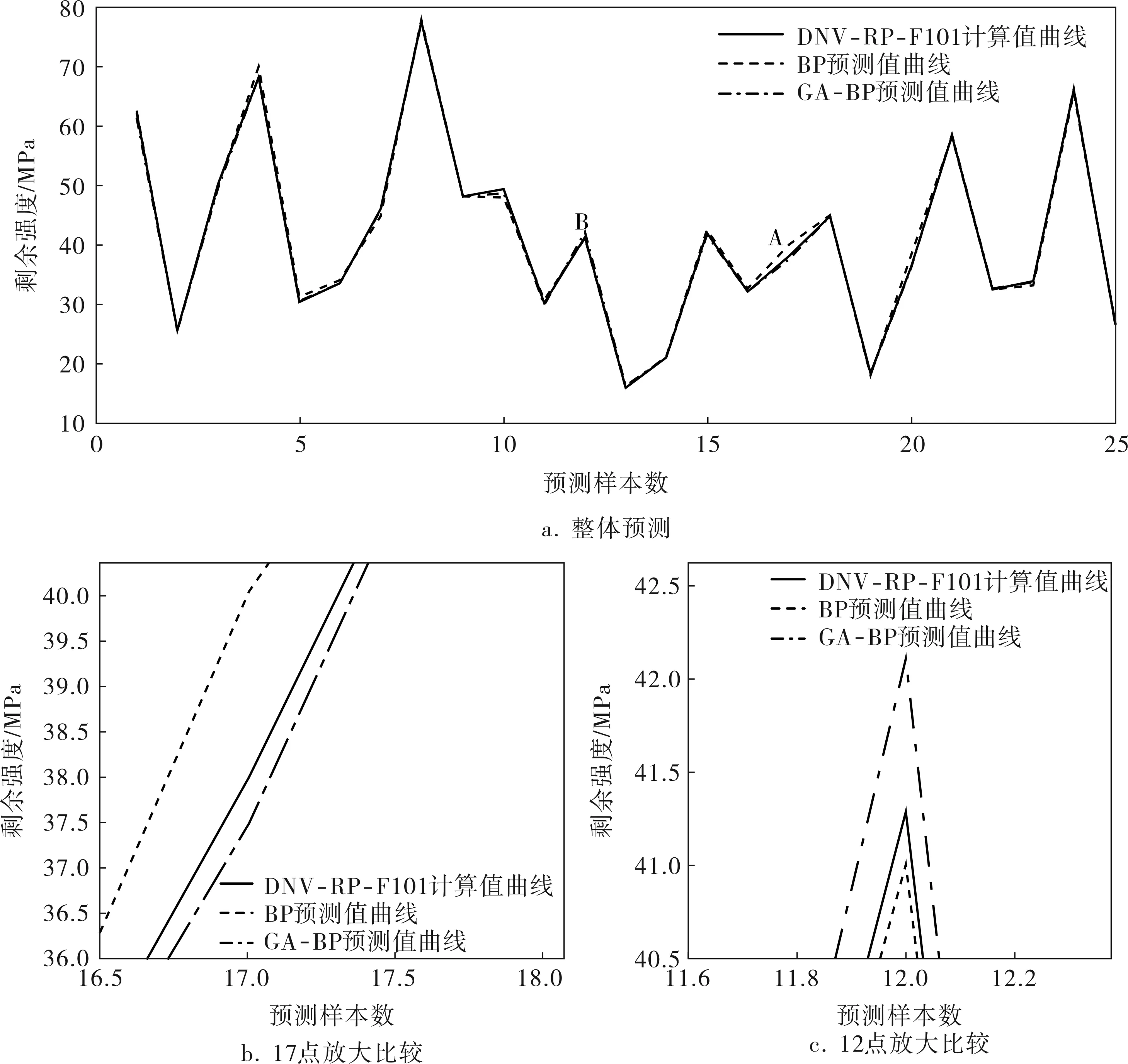
图4 不同神经网络预测值曲线与DNV-RP-F101计算值曲线比较
神经网络训练结束后,为了检验网络的泛化性,引用了文献[10]中的试验数据,分别在训练好的BP神经网络模型和GA-BP神经网络模型上进行预测,预测结果的对比值见表1。其中Δ1、Δ2、Δ3分别为DNV-RP-F101标准计算值、BP神经网络和GA-BP神经网络预测值与试验值间的相对误差。可以看出,相对于DNV-RP-F101计算值,人工神经网络预测值更加接近试验值。经过最大相对误差比较可知,GA-BP神经网络预测最大相对误差为4.86%,其误差要低于DNV-RP-F101计算最大相对误差为12%和BP神经网络预测最大相对误差为7.91%。因此,利用人工神经网络预测腐蚀管道剩余强度的方法是可行的,且GA-BP神经网络可以更好地满足工程需要。
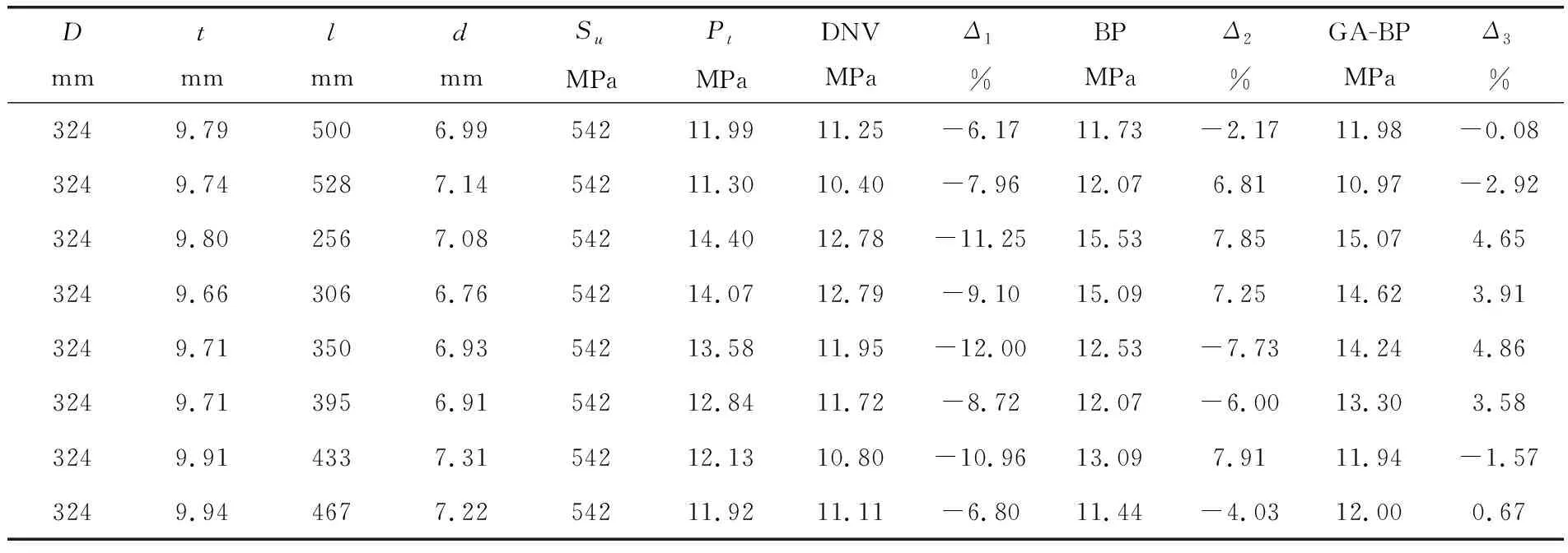
表1 DNV-RP-F101计算值和不同神经网络预测值与试验结果比较

(续表1)
4 结束语
依据BP神经网络所具有的非线性和较强的泛化能力,建立了管径、壁厚、腐蚀缺陷长度、腐蚀缺陷深度以及管材极限抗拉强度等影响因素与腐蚀海洋立管剩余强度之间的BP神经网络预测模型,在BP神经网络模型的基础上,利用遗传算法优化BP神经网络的权值和阈值,构建GA-BP神经网络模型。在25组测试样本中,BP神经网络和GA-BP神经网络预测的相对误差分别控制在5.384%和1.995%以内。结果表明,利用人工神经网络来预测腐蚀海洋立管的剩余强度是可行的。此外,在对神经网络进行训练时,BP神经网络需要经过194次训练达到训练目标,而GA-BP神经网络只需要17次就能达到训练目标。由此可见,利用遗传算法优化BP神经网络模型不仅可以有效地提高网络的训练精度,而且还可提高其收敛速度,是一种更加科学、有效的预测模型。
[1] 高照杰, 粟京. 带损伤海底石油管线的安全评估[J]. 海洋工程, 2003, 21(1): 53~59.
[2] ASME B31G,Manual of Determining the Remaining Strength of Corroded Pipelines-A Supplement to ANSI/ASME B31G Code for Pressure Piping[S]. NewYork: American Society of Mechanical Engineers, 1991.
[3] API RP579, Recommended Practice for Fitness-For-Service[S]. America: American Petroleum Institute, 2000.
[4] BS 7910, Guidance on the Method for Assessing the Acceptability for Flaws in Fusion Welded Structure[S]. London: British Standard Institute, 1999.
[5] DNV. Recommend Practice, RP-F101, Corroded Pipelines[S]. Norway: Det Norske Veritas, 2004.
[6] CAN / CSA-Z184-M86, Gas Pipeline System[S]. Canada: Canadian Standards Association, 1886.
[7] 刘亚莉,张强,赵丽丽,等. 基于MATLAB的螺旋槽干气密封性能分析[J]. 化工机械, 2012, 39(1): 41~43.
[8] SilvaR C C, Guerreiro J N C, Loula A F D. A Study of Pipe Interacting Corrosion Defects Using the FEM and Neural Networks[J]. Advances in Engineering Software, 2007, 38 (11/12):868~875.
[9] 周毅, 徐伯龄. 神经网络中的正交设计法研究[J]. 南京大学学报(自然学科版,) 2001, 37(1) : 72~78.
[10] Freire J L F, Vieira R D, Castro J T P. Part3: Burst Tests of Pipeline with Extensive Longitudinal Mental Loss[J]. Experimental Techniques, 2006, 30(6): 60~65.

