螺栓法兰连接模糊可靠性数值计算方法*
孙振国 顾伯勤
(1.江苏省特种设备安全监督检验研究院无锡分院;2.南京工业大学机械与动力工程学院)
在对工程结构进行可靠性分析时,随机性和模糊性均对结构的可靠性有影响,如果某一环节存在一定的模糊性,应考虑分析其模糊可靠性。在密封紧密性分析中,当实际泄漏率接近于指标泄漏率两侧时,很难判断此时的密封状态。密封从紧密到泄漏失效是一个逐渐变化的过程,即在指标泄漏率附近存在一个模糊区域;同样,由于设计、生产及贮存等因素的影响,材料的强度具有分散性,在螺栓和法兰材料许用应力的两侧也存在相应的模糊区域。因此,螺栓法兰连接的可靠性是模糊可靠性。
Arghavani J等提出一种用于垫片选型和泄漏率预测的模糊逻辑法和模糊决策系统[1~3]。陈永林和顾伯勤提出了密封可靠性概念,依据干涉模型的基本原理,利用反应论模型推导出密封可靠性计算公式,但未考虑密封状态的模糊性[4]。张庆雅等研究了理想情况下火箭发动机法兰系统的密封模糊可靠性,建立的极限状态方程并不是以指标泄漏率作为评价依据,而是以O形橡胶圈上的垫片应力和介质压力为依据判断其是否达到密封要求[5]。笔者综合考虑连接结构的随机性和模糊性,以泄漏特性和强度为准则,建立了螺栓法兰连接的模糊可靠性计算模型,并提出了一种基于有限元的螺栓法兰连接模糊可靠性计算方法,并对该方法进行了验证。
1 螺栓法兰连接模糊可靠性串联模型
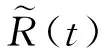
(1)
为了分析密封性能的模糊可靠性,可以借助垫片时效泄漏模型计算连接系统的泄漏率[6]:
(2)
式中AL、BL、CL、α、nL——回归系数;
l——垫片有效密封宽度,mm;
pd——介质出口压力,MPa;
pm——介质进口压力,MPa;
ps——介质平均压力,MPa;
SG——操作时垫片应力,MPa;
SK——预紧时垫片应力,MPa;
T——温度,K;
t——时间,s;
η′——流体动力粘度,MPa·s。
在指标泄漏率的两侧存在一个模糊区域,选用模糊三角形隶属函数描述指标泄漏率的模糊性,表示为:
(3)
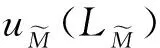
LC——传统指标泄漏率;
LM——模糊指标泄漏率。
对于不同的截集水平λ,隶属函数的参数可表示为:
(4)
根据应力强度干涉模型和模糊可靠性理论,建立考虑指标泄漏率模糊性的密封可靠性极限状态方程:
(5)
(6)
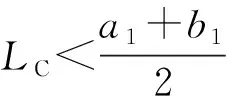
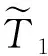
2 螺栓法兰连接模糊可靠性数值计算方法
2.1 极限状态方程的模糊化处理
传统的Monte-Carlo方法忽略了连接系统各部分应力的真实分布和可靠性指标的模糊性,只能计算理想状态下垫片密封的可靠性[7],无法直接用于计算连接系统的模糊可靠性。对考虑指标泄漏率模糊性的式(5)在零点附近进行模糊化处理,得到新的极限状态方程:
(7)
(8)
(9)
同理,螺栓强度可靠性在零点附近进行模糊化处理的极限状态方程可以表示为:
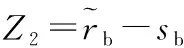
(10)
(11)
(12)
法兰强度可靠性在零点附近进行模糊化处理的极限状态方程可以表示为:
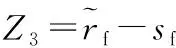
(13)
(14)
(15)
2.2 螺栓法兰连接模糊可靠性计算模型
ANSYS提供的概率统计分析功能不能直接分析螺栓法兰连接的模糊可靠性,但可以在极限状态方程模糊化的基础上,根据式(7)~(12)建立适合求解的计算模型,即通过数学变换将模糊可靠性转化为常规可靠性问题进行求解。
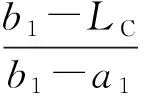
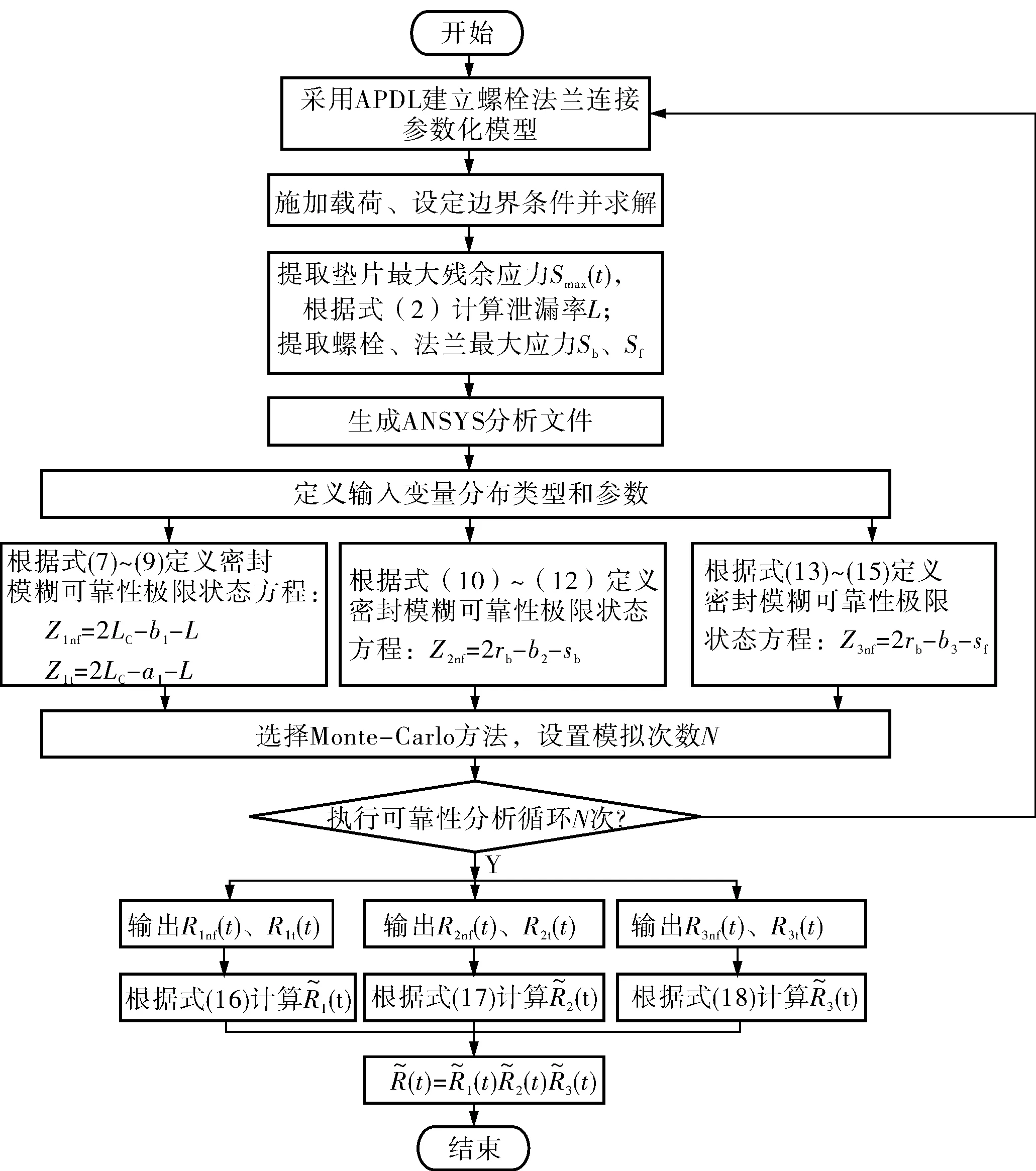
图2 螺栓法兰连接模糊可靠性分析流程
密封、螺栓和法兰强度的模糊可靠性计算模型分别为:
(16)
(17)
(18)
螺栓法兰连接在不同服役时间下的模糊可靠性计算模型为:
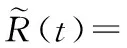
(19)
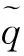
(20)
T(*)={LC,rb,rf}
2.3 基于有限元的螺栓法兰连接模糊可靠性计算方法
利用有限元分析软件ANSYS的概率分析功能及其参数化设计语言APDL实现自动循环计算和统计功能,采用Monte-Carlo方法对极限状态方程进行求解。当垫片残余应力沿周向均匀分布,而沿径向不均匀分布时,泄漏率的大小不仅依赖于垫片有效接触宽度,而且依赖于垫片最大接触应力[6]。将垫片径向节点最大应力Smax(t)代入式(2)计算当前泄漏率。对于螺栓和法兰的强度可靠性,可通过极限载荷法确定螺栓和法兰应力必须满足的强度条件[7, 8]。根据第三强度理论,当螺栓中最大的当量应力超过螺栓材料的模糊许用应力时即为强度失效;根据第四强度理论,当法兰中的最大Mises等效应力超过法兰材料的模糊许用应力时为强度失效,将单元最大应力代入极限状态方程进行分析。
3 算例
某石化企业一管道螺栓法兰连接,工作压力为330kPa,温度为693K,介质为氢气、硫化氢气体和碳氢混合物。法兰为符合GB/T 9115.1-2000的PN4.0MPa、DN300mm的对焊凸面法兰,材料为10CrMo910。采用16个M30、材料为25CrMoVA的双头螺栓。垫片采用符合GB/T 19066.1-2008的柔性石墨复合垫片,内径为323mm,外径为363mm,压力为40MPa。规定指标泄漏率为0.02cm3/s,计算误差e为1×10-4。该连接系统已使用一年,计算该螺栓法兰连接的模糊可靠度。
不同截集水平下隶属函数参数值的计算式为:
(*)={LC,rb,rf}
参照文献[6]中的方法建立参数化有限元模型,根据图2所示流程进行螺栓法兰连接的模糊可靠性分析。取不同隶属函数参数(a,b),该螺栓法兰连接系统使用一年后在不同截集水平λ下的模糊可靠度见表1~3。

表1 (a=(1-3%)(*),b=(1+5%)(*))时,不同截集水平下螺栓法兰连接的模糊可靠度

表2 (a=(1-5%)(*),b=(1+5%)(*))时,不同截集水平下螺栓法兰连接模糊可靠度

表3 (a=(1-5%)(*),b=(1+3%)(*))时,不同截集水平下螺栓法兰连接模糊可靠度
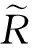
4 结束语
从密封模糊可靠性和强度模糊可靠性的出发,推导出螺栓法兰连接模糊可靠性模型,通过对极限状态方程进行模糊化处理,提出了基于Monte-Carlo法和有限元的螺栓法兰连接模糊可靠性数值计算方法。并对一螺栓法兰连接的模糊可靠性进行了分析,结果表明连接系统的模糊可靠性主要由密封模糊可靠性决定,且模糊性对螺栓法兰连接的可靠度有较大影响。服役一年后,连接系统的可靠性显著降低。
[1] Arghavani J, Derenne M, Marchand L. Sealing Performance of Gasketed Bolted Flanged Joints: A Fuzzy Decision Support System Approach[J]. International Journal of Advanced Manufacturing Technology, 2001, 17 (1): 2~10.
[2] Arghavani J, Derenne M, Marchand L. Fuzzy Logic Application in Gasket Selection and Sealing Performance[J]. International Journal of Advanced Manufacturing Technology, 2001, 18 (1): 67~78.
[3] Arghavani J, Derenne M, Marchand L. Prediction of Gasket Leakage Rate and Sealing Performance Through Fuzzy Logic[J]. International Journal of Advanced Manufacturing Technology, 2002, 20 (8): 612~620.
[4] 陈永林,顾伯勤. 垫片密封的可靠性分析方法[J]. 润滑与密封,2001,(2):24~25.
[5] 张庆雅,汪亮,杨光松.理想情况下火箭发动机法兰系统密封模糊可靠性分析[J]. 弹箭与制导学报,2005,25(4):548~551.
[6] Sun Z G, Gu B Q. Prediction of Time-correlated Leakage Rates of Bolted Flanged Connections by Considering the Maximum Gasket Contact Stress[J]. Journal of Pressure Vessel Technology, 2012, 134(1): 1~7.
[7] 张庆雅,汪亮. 垫片螺栓法兰连接系统的强度可靠性分析[J]. 机械科学与技术,2003,22(z1):79~83.
[8] 孙世锋. 承受外弯矩作用的螺栓法兰接头的研究[D]. 上海:华东理工大学,2004.

