利用Chebyshev小波解Fredholm-Volterra积分方程
邢红娟,曲小钢
(西安建筑科技大学 理学院,陕西 西安 710055)
1 Chebyshev小波
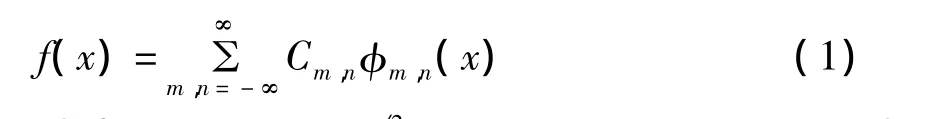
式中 φm,n(x)=2m/2φ(2mx-n),m,n∈z,m为尺度值,n为平移量。
平移和伸缩的小波函数可以构成函数基或函数框架,足够多的平移和伸缩的小波函数加权和能够有效地逼近能量有限的函数。
Chebyshev小波函数 φn,m(t)= φ(k,n,m,t),含有4 个变量,t为时间,n=1,2,…,2k-1,k为任意的正整数,m为第一类Chebyshev多项式的阶数,区间[0,1)上的Chebyshev小波定义为
小波函数[1-2]在时域和频域[3]均具有较强的局部性,可以构成具有多分辨率特征的函数空间序列,任意函数f(x)都可以被分解为平移和伸缩的小波函数φ(x)的线性和,即:
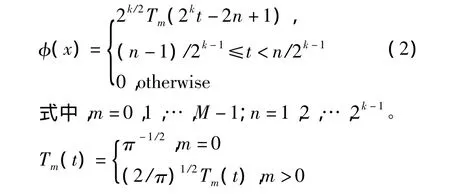
Tm(t)为阶数为m的Chebyshev多项式,存在权值函数 ω(t)=1/(1 -t2)1/2,t∈(-1,1),使 Chebyshev多项式正交。
对于Chebyshev小波,权值函数ω(t)变为
ωn(t)=ω(2kt-2n+1)。
2 Fredholm-Volterra积分方程的矩阵化
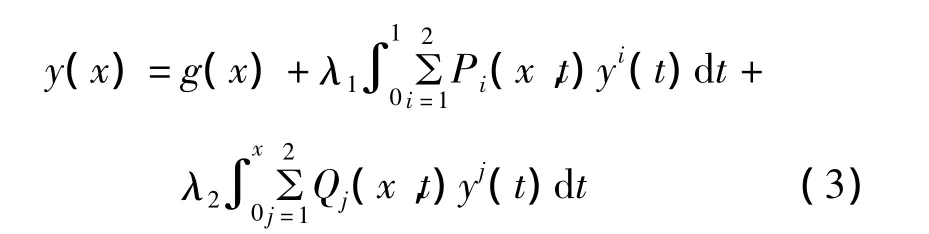
这里y(x)是未知函数,函数g(x),Pi(x,t),Qj(x,t)是定义在区间 0≤x,t≤1 上的,且pij,qij,rij,λ1,λ2,μi是常量。
上述关系的y(x)可以用Chebyshev多项式形式表示,即

这里(x)=Tr(2x-1),ar,0≤r≤N是未知的Chebyshev系数,N是任意的正整数m≤N,Tr(x)为阶数为r的第一类Chebyshev多项式,这里Chebyshev配置点[4]定义为

(4)式可以用以下矩阵形式表达,即
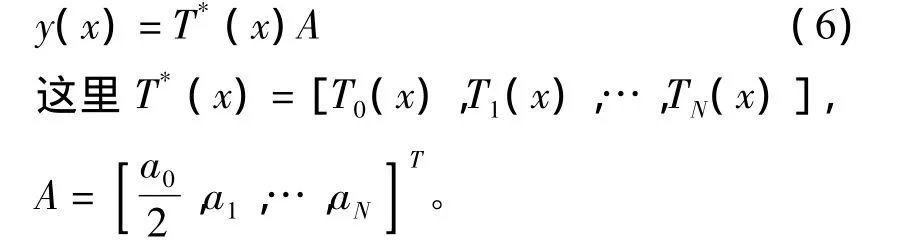
2.1 将Fredholm积分部分用矩阵表示法表示
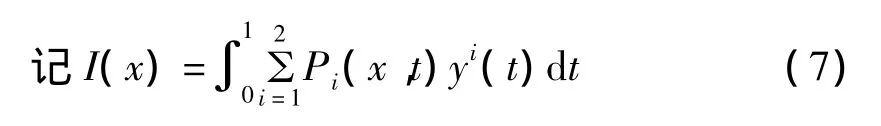
将Chebyshev配置点代入(7)式得到I(x1)的矩阵关系,对于每个xs,P0(x,t),P1(x,t)以如下形式扩展成Chebyshev基数

这时Pi(xs,t)的矩阵表达形式变为

另外,函数y2(t)能以矩阵形式写出

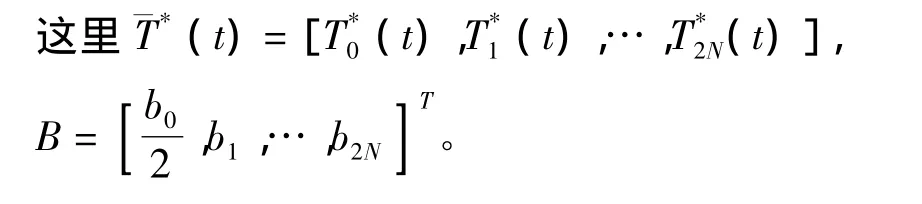
B中的元素由以下关系给出
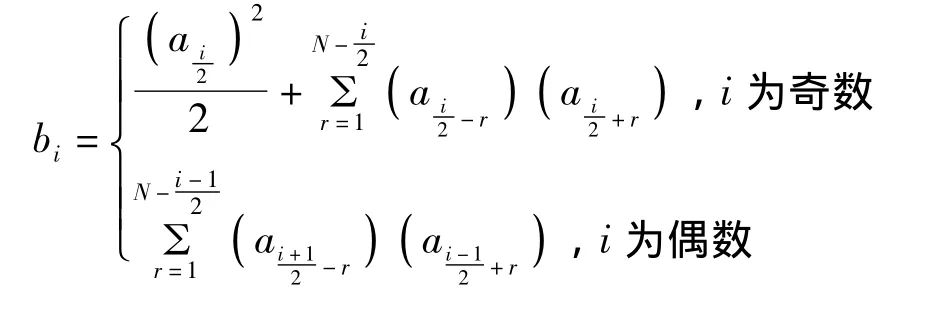
又由(6),(8),(9)得
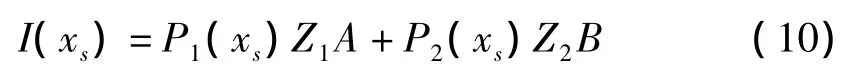
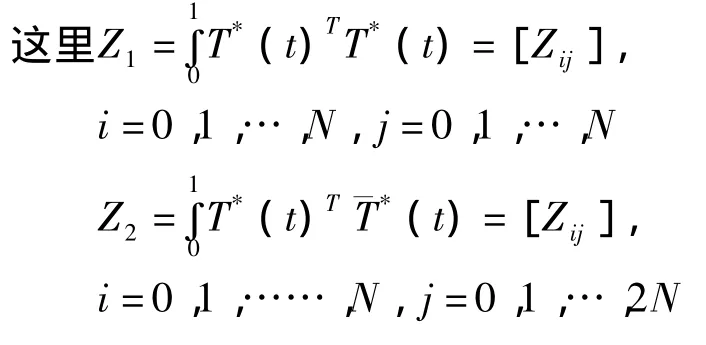
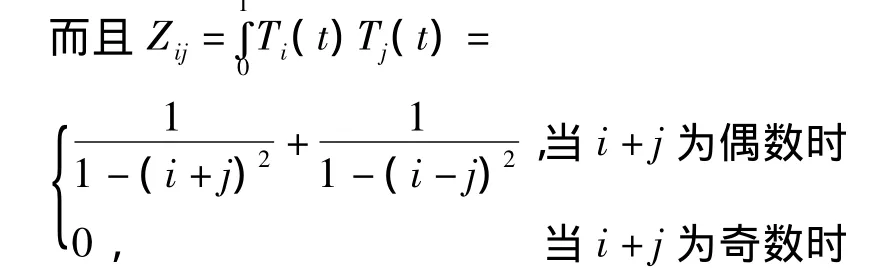
2.2 将Volterra积分部分用矩阵表达

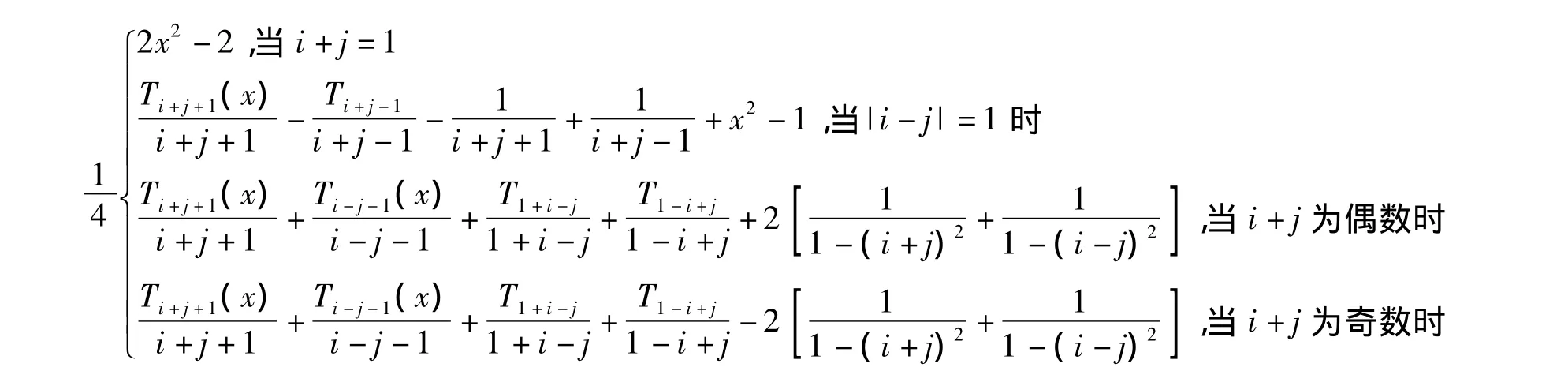
将(6),(10),(12)代到(3)有

在本文,Chebyshev小波配置点法运用在积分方程中,解决Fredholm积分部分比解决Volterra积分部分更容易些,这个方法的一个优势是运用截断的Chebyshev小波系数,这样y(x)可以由任意的数值所表达,从而使计算简化。
[1]樊启斌.小波分析[M].武汉:武汉大学出版社,2008.
[2]魏明果.实用小波分析[M].北京:北京理工大学出版社,2005.
[3]王文兰,凌呼君,冯永祥.广义预测控制(GPC)在单元机组中参数的优化[J].微计算机信息,2007,23(4-1):99-105.
[4]A.Akyiiz,M.Sezer,A Chebyshev collocation method for the solution Linear integro differential equation,J.Comput,Math.1999(72):491 -507.
[5]M.Sezer,S.Dogan,Chebyshev series solution of Fredholm Integral equation,Int.J.Math.Educ.Sci.Technol,1996(27):649-657.
[6]K.Maleknejad,Y,Mahmoudi,Taylor polynomial solution of high-order nonlinear Volterra-Fredholm integro-differential equations,Appl.Math.Comput.2003(145):641 -653.
[7]B,Sepdhrian,M,Razzaghi,Single - term Walsh series method for the Volterra integro- differential equations,Engineering Analysis with Boundary Elements,2004(28):1315 -1319.

